Курс практичксих занятий по инженерной термодинамики. параметры состояния тела

• Название: параметры состояния тела
• Дата: 05.11.2022
• Размер: 1.52 Mb.
• Имя файла: Курс практичксих занятий по инженерной термодинамики.doc
• Тип: Занятие; #770814
• страница: 3 из 7

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3.

ТЕМА: « ГАЗОВЫЕ СМЕСИ »
Состав газовой смеси определяется количеством каж­дого из газов, входящих в смесь, и может быть задан мас­совыми или объемными долями.

Массовая доля определяется отношением массы отдельного газа, входящего в смесь, к массе всей смеси:

m₁ = , m₂ = , m₃ = , …, m_n= , (3.1)

где М₁, М₂,, М₃, . . ., М_п— массы отдельных газов и М — масса всей смеси.

Объемной долей газа называют отношение объема каждого компонента, входящего в смесь, к объему всей газовой смеси при условии, что объем каждого компонента отнесен к давлению и температуре смеси (приведенный объем):

r₁ = , r ₂ = , r ₃ = , …, r _n = , (3.2)

где V₁ , V₂ ,V₃ ,V_n — приведенные объемы компонен­тов газов, входящих в смесь; V— общий объем газовой смеси.

Очевидно, что М₁ +М₂ +М₃ +… + М_п= М;

т₁ + т₂+ т₃ +…+ т_п= 1,

а также

V ₁ +V ₂ +V ₃ +…+V_n =V;

r₁ + r₂ + r₃ + …+ r_n = 1

Для перевода массовых долей в объемные пользуются формулой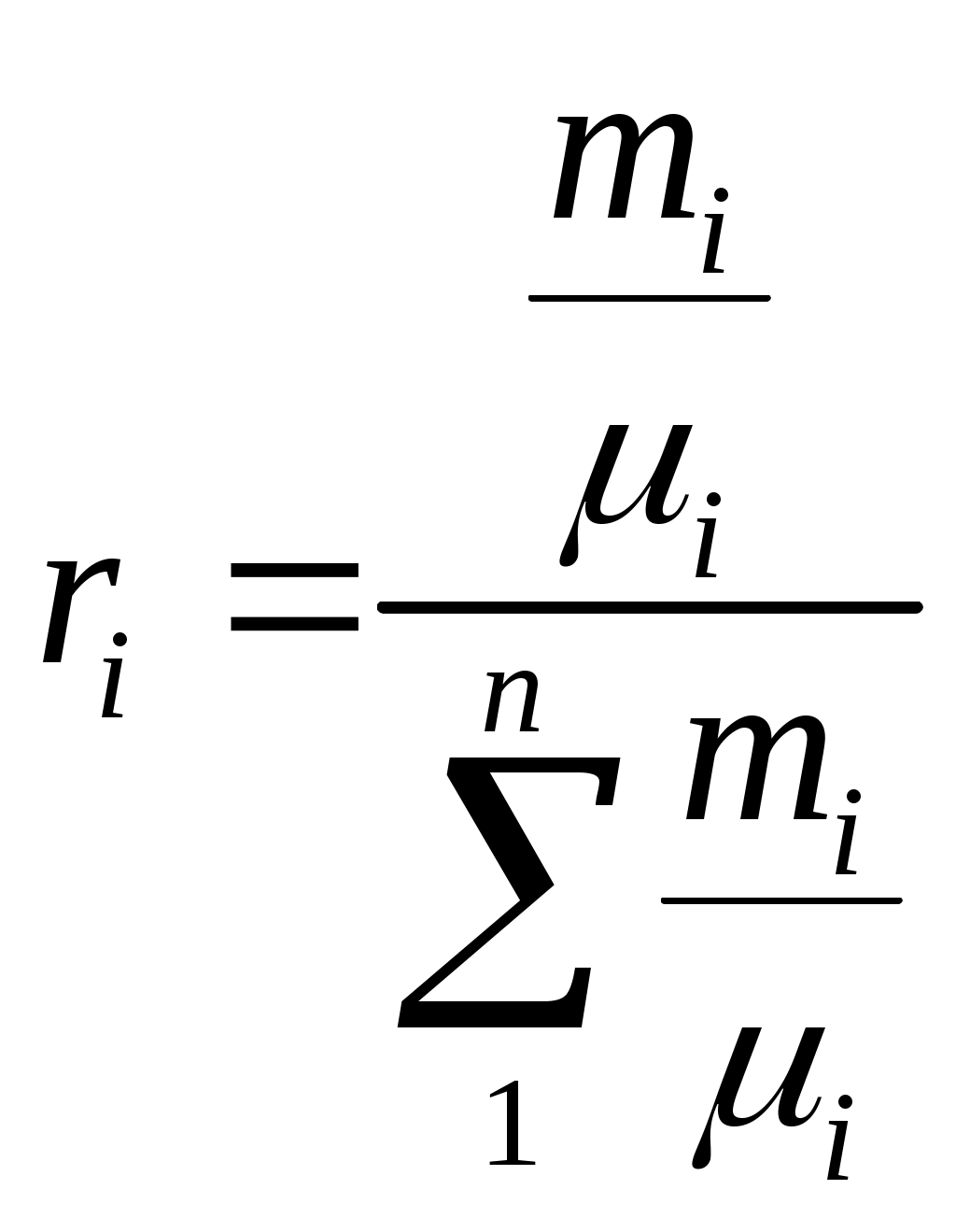

. (3.3)

Объемные доли переводят в массовые по формуле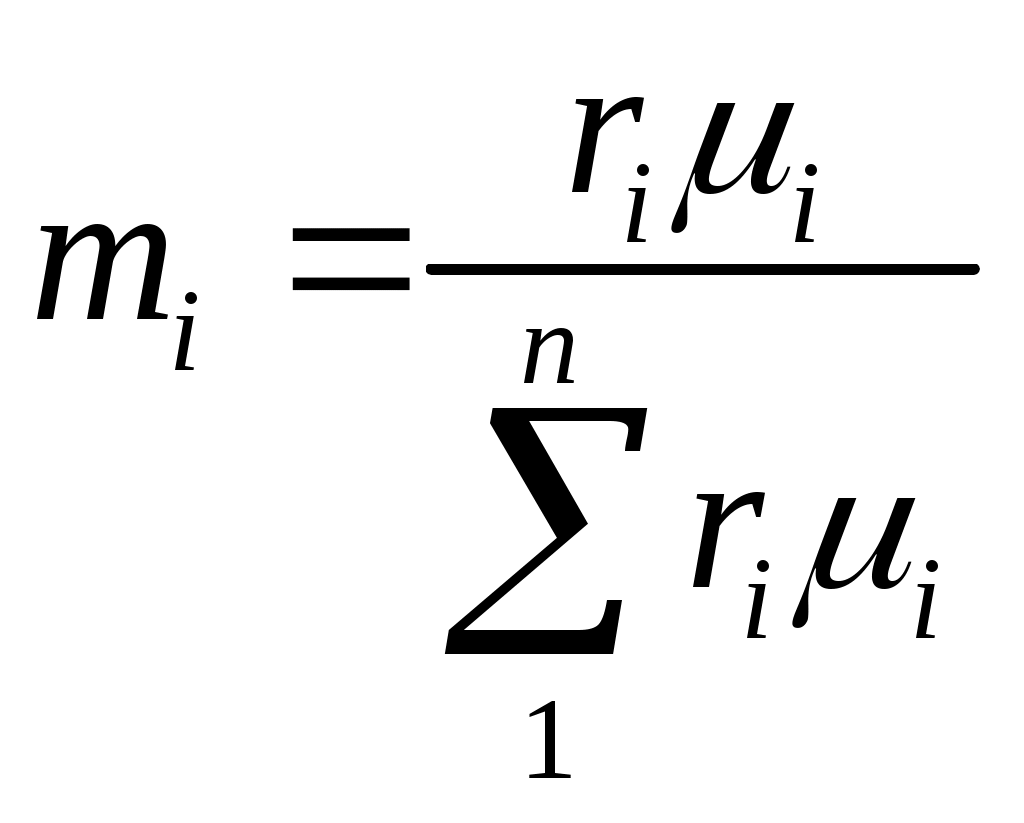

(3.4)

Плотность смеси определяют из выражения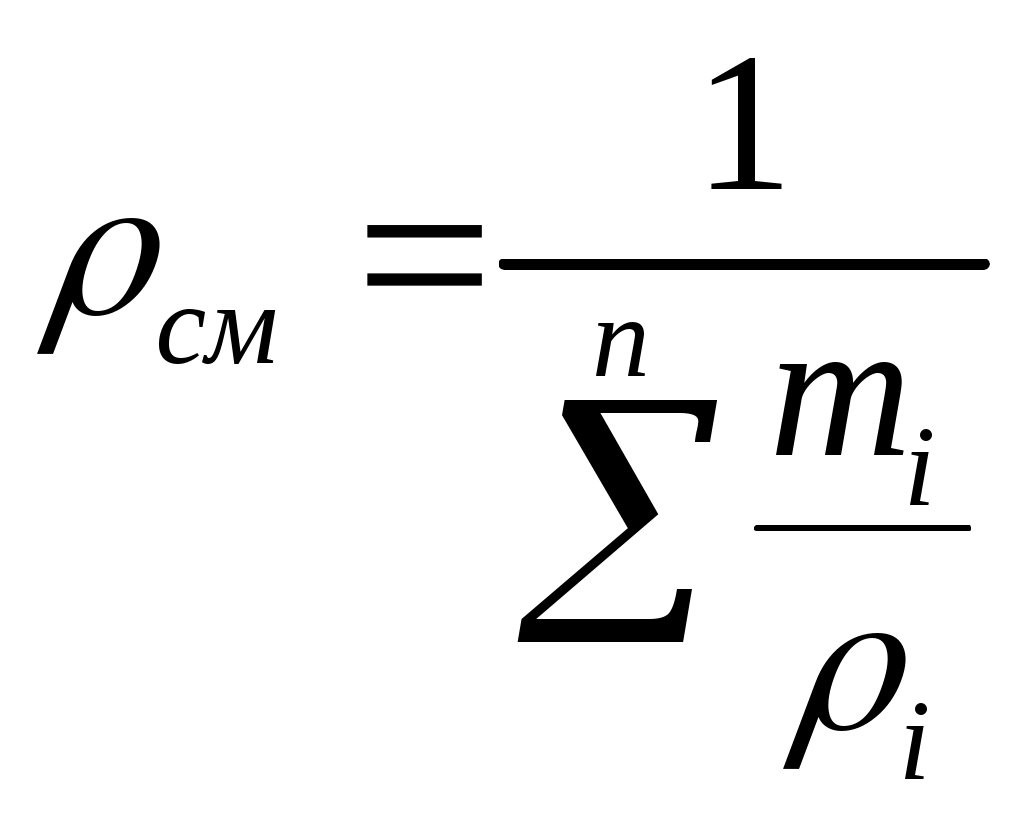

, кг/м³ (3.5) или, если известен массовый состав, по формуле

(3.6)

Удельный объем. смеси представляет величину, обратную ρ_сл,; поэтому, если дан объемный состав смеси, то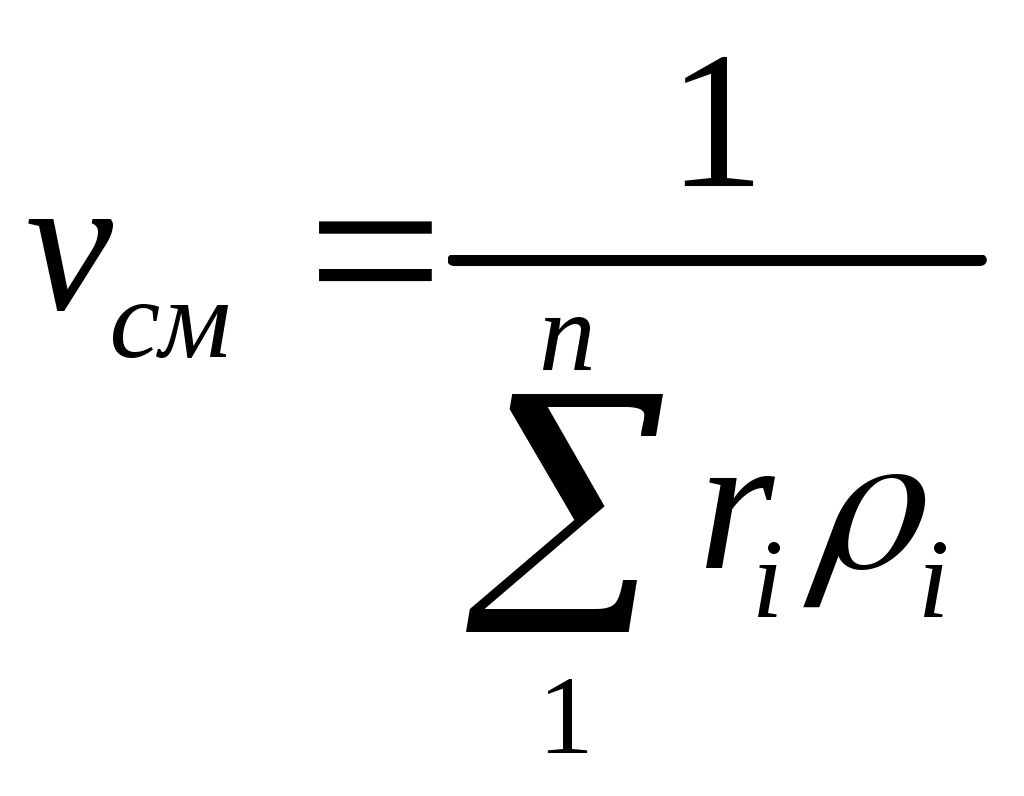

, м³/кг (3.7)

Если же известен массовый состав, то

, м³/кг (3.8)

Из уравнения (3.5) легко получить значение так называемой кажущейся молекулярной массы газовой смеси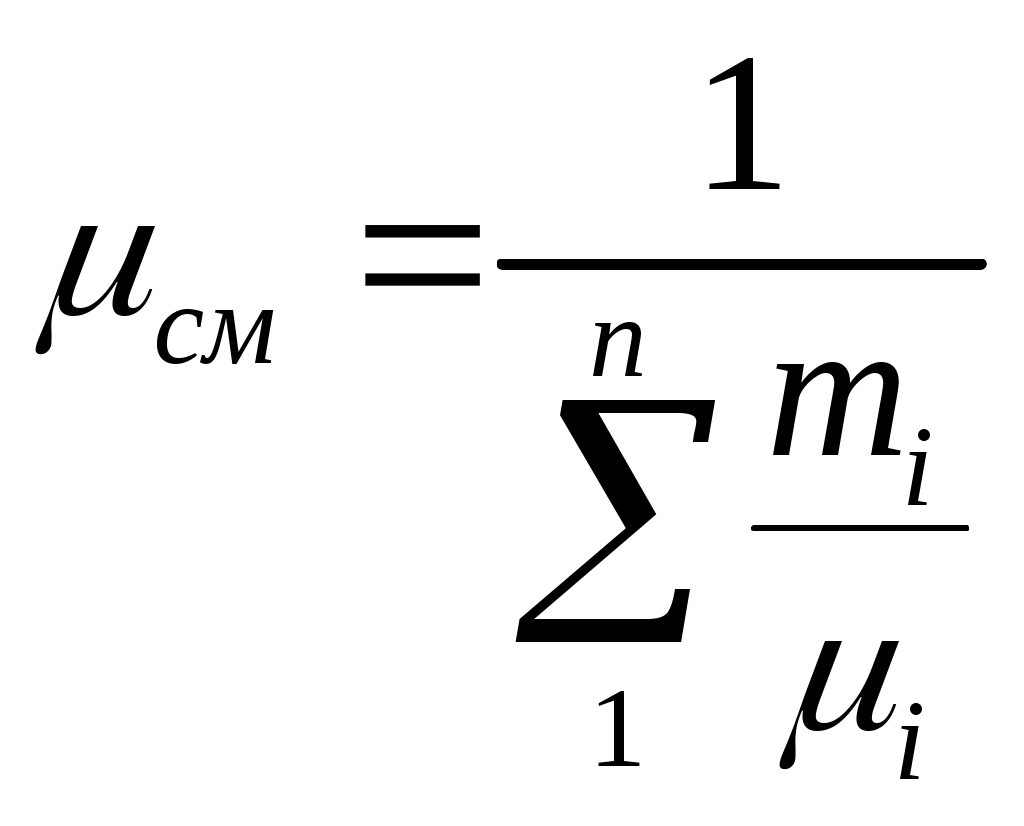

(3.9) или через массовый состав

(3.10)

Газовую постоянную смеси газов (R_см) можно выразить или через газовые постоянные отдельных компонентов., входящих в смесь, или через кажущуюся молекулярную массу смеси

Дж/(к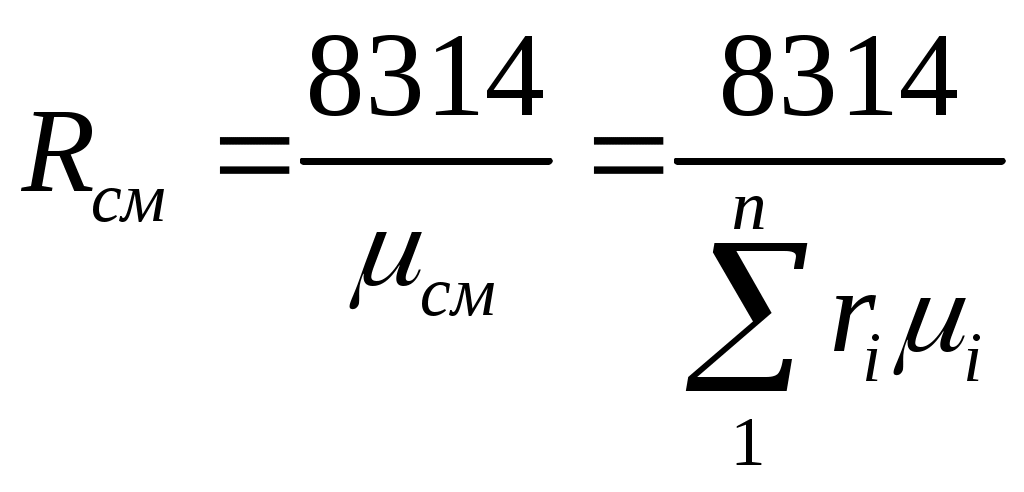г·К), (3.11)

или

Дж/(кг·К) (3.12)

Связь между давлением газовой смеси и парциальными давлениями отдельных компонентов, входящих в смесь, устанавливается следующей зависимостью (закон Даль­тона), легко получаемой из основного уравнения кинетической теории газов:

p=р₁+р₂+р₃+•••+р_n, (3.13)

где p - общее давление газовой смеси;

р₁, р₂,…,р_n - парциальные давления отдельных компонентов, входящих в смесь.

Парциальные давления определяются проще всего, если известны объемные доли отдельных компонентов, входящих в смесь;

p₁=pr₁, p₂=pr₂ и т.д.

или вообще

р_i=pr_i, (3.14)

где р_l -парциальное давление любого газа, входящего в смесь.

Если известны массовые доли, то парциальнoe давле­ние любого газа, входящего в смесь,

. (3.15)

Задачи

3.1. Атмосферный воздух имеет примерно следующий массовый состав: т_о2=23,2%, т_N2=76,8%. Определить объемный состав воздуха, его газовую постоянную, кажущуюся молекулярную массу и парциальные давления кислорода и азота. Если давление воздуха по барометру В=101325 Па.

3.2. B 1 м³ суxого воздуха содержится примеpно 0,21 м³ кислорода и 0,79 м³ азота. Определить массовый состав воздуха, его газовую постоянную и парциальные давления кислорода и азота.
3.3. Смесь газов состоит из водорода и окиси yглерода. Массовая доля водорода тн₂ = 0,67°,%. Найти газовую постоянную смеси и ее удельный объем при нoрмальных условиях.
3.4. Определить газовую постоянную смеси газов, со­стоящей из 1 м^з генераторного газа и 1,5 м^з воздуха, взя­тых при ноpмальных условиях, и найти парциальные давления составляющих смеси. Плотность генерaторного газа ρ принять равной 1,2 кг/м^з.
3.5. Объемный состав сухих продуктов сгоpания топ­лива (не содержащих водяных варов) следующий: СО₂ = = 12,3°/о; 0₂ = 7,2%; N₂ = 80,5%. Найти кажущуюся молекулярную массу и газовую постоянную, a также плотность и удельный объем продук­тов сгорания при B = 100 кПа и t = 800° C.
3.6. Генераторный газ имеет следующий объемный со­став: Н₂ = 7,0%; СН₄ = 2,0%; CO = 27,6%; СО₂ = 4,8%; N₂ = 58,6%. Определить массовые доли, кажущуюcя молекулярную массу, газовую постоянную, плотность и парциальные давления при 15^° C и 0,1 МПа.

3.7. Газ коксовых печей имеет следующий объемный состав: Н₂ = 57%; СН₄ = 23%; СО = 6%; СО₂ = 2°о; N₂ = 12%. Найти кажущуюся молекулярную массу, массовые доли, газовую постоянную, плотность и парциальные давления при 15° C и 100 кПа.

3.8. Генераторный газ состоит из следующих объемных
частей: Н₂ = 18%; СО = 24%; СО₂ = 6%; N₂ = 52%.
Определить газовую постоянную генераторного газа и массовый состав входящих в смесь газов.

3.9. Анализ продуктов сгорания топлива, произведен­ный c помощью аппарата Орса, показал следующий их состав; rco2=12,2%; ro₂=7,1%; rco=0,4%; r_N2=80,3%. Найти. массовый состав входящих в смесь газов.

3.10. Определить газовую постоянную, плотность при нормальных условиях и объемный состав смеси, если ее массовый состав следующий: H₂ = 8,4 % ; СН₄ = 48,7 % ;С₂Н₄ = 6,9%; СО = 17%; СО₂ = 7,6%; 0₂ = 4,7%; N₂= 6,7^°%.
3.11. Найти газовую постоянную, удельный объем газо­вой смеси и парциальные давления ее составляющих, если объемный состав смеси следующий: С0₂ = 12%; СО = 1%; Н₂0 = 6%; 0₂ = 7%; N₂ = 74%, а общее давление ее р = 100 кПа.
3.12. B резервуаре емкостью 125 м^з находится коксовый газ при давлении р = 0,5 МПа и температуре t = 18° C. Объемный состав газа следующий:

гн₂ = 0,46; гсн₄ = 0,32; rco = 0,15; r_N2 = 0,07. После израсходования некотоpого количества гaзa давление его понизилось до 0,3 МПа, a темперaтура - до 12 C. Определить массу израсходованного коксового газа.
3.13. Массовый состав смеси следyющий: СО₂ = 18%; О₂ = 12% и N₂ = 70%.

До какого давления нужно сжать эту смесь, находя­щуюся при нормaльных условиях, чтобы при t = 180° C 8 кг ее занимали объем, равный 4 м³.
3.14. Определить массовый состав газовой смеси, со­стоящей из углекислого газа и азота, если известно, что парциальное давление углекислого газа р_со2 = 120 кПа, a давление смеси р_см = 300 кПа.
3.15. Газовая смесь имеет следующий массовый состав: СО₂ = 12%; 0₂ = 8% и N₂ = 80%. До какого давления нужно сжать эту смесь, находя­щуюся при нормальных условиях, чтобы плотность ее составляла 1,6 кг/м^з

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4.
ТЕМА: «ТЕПЛОЕМКОСТЬ ГАЗОВ »
Теплоемкостью называют количество теплоты, которое необходимо сообщить телу (газу), чтобы повысить темпе­ратуру какой-либо количественной единицы на 1° С.

За единицу количества энергии в системе СИ приме­няют джоуль (Дж). В системе СИ джоуль является уни­версальной единицей, применяемой для измерения всех видов энергии: тепловой, механической, лучистой и пр. В качестве тепловой единицы 1 Дж представляет собой такое ее количество, которое появляется в результате превращения механической работы 1 Дж в теплоту. В качестве единицы механической энергии джоуль пред­ставляет собой работу, совершаемую силой, равной 1 нью­тону при перемещении ею тела на расстояние 1 м в направ­лении действия силы (1 Дж = Н-м = 1 кг-м²/с²).

В зависимости от выбранной количественной единицы вещества различают мольную теплоемкость μc— кДж/(кмоль К), массовую теплоемкость с — кДж/(кг-К) и объемную теплоемкость с' — кДж/(м³-К).

Как было указано выше, 1 м³ газа в зависимости от параметров его состояния имеет разные массы. В связи с этим объемную теплоемкость всегда относят к массе газа, заключенной в 1 м⁸ его при нормальных условиях (р_н= 101 325 Па (760 мм рт. ст.) и Т _н = 273 К (t _н = 0°С).

Для определения значений перечисленных выше теплоемкостей достаточно знать величину одной какой-либо из них. Удобнее всего иметь величину мольной теплоем­кости. Тогда массовая теплоемкость

с= , (4.1)

а объемная теплоемкость

с^/ = (4.2)

Объемная и массовая теплоемкости связаны между собой зависимостью

с^/ = с ·ρ_н

где р_н — плотность газа при нормальных условиях.

Теплоемкость газа зависит от его температуры. По этому признаку различают среднюю и истинную тепло­емкость.

Если q— количество теплоты, сообщаемой единице количества газа (или отнимаемого от него) при изменении температуры газа от t₁до t₂(или, что то же, от T₁ до Т₂), то

c_m = (4.3)

представляет собой среднюю теплоемкость в пределах t₁ - t₂ . Предел этого отношения, когда разность темпера­тур стремится к нулю, называют истинной теплоем­костью. Аналитически последняя определяется как с=

Теплоемкость идеальных газов зависит не только от их температуры, но и от их атомности и характера процесса. Теплоемкость реальных газов зависит от их природных свойств, характера процесса, температуры и давления.

Для газов особо важное значение имеют следующие два случая нагревания (охлаждения):

1) изменение состояния при постоянном объеме;

2) изменение состояния, при постоянном давлении.

Обоим этим случаям соответствуют различные зна­чения теплоемкостей.

Таким образом, различают истинную и среднюю тепло­емкости:

а) мольную — при постоянном объеме (μс_v и μc_vm) и постоянном давлении (μc_p и μс_рт);

б) массовую — при постоянном объеме (с_vи c_vm) и постоянном давлении (с_pи с_рт);

в) объемную—при постоянном объеме (c'_vи c'_vm) и постоянном давлении (с'_ри с'_рт).

Между мольными теплоемкостями при постоянном давлении и постоянном объеме существует следующая зависимость:

μc_p— μc_v= μR 8,314 кДж/(кмоль-К). (4.4)

Для приближенных расчетов при невысоких темпера­турах можно принимать следующие значения мольных теплоемкостей (табл. 4.1).
Таблица 4.1 Приближенные значения мольных теплоемкостей при постоянном объеме и постоянном давлении (с= cоnst)

Газы	Теплоемкость в кДж/(кмоль-К)
	μсv	μcp
Одноатомные………	12,56	20,93
Двухатомные ………	20,93	29,31
Трех- и многоатомные . . .	29,31	37,68

В технической термодинамике большое значение имеет отношение теплоемкостей при постоянном давлении и постоянном объеме, обозначаемое буквой k:

k =

Если принять теплоемкость величиной постоянной, то на основании данных таблицы 4.1 получаем: для одноатомных газов k=1,67; для двухатомных газов k=1,4; для трех- и многоатомных газов k=1,29.

Теплоемкость газов изменяется с изменением температуры, причем эта зависимость имеет криволинейный характер.

Количество теплоты, которое необходимо затратить в процессе нагревания 1 кг газа в интервале температур от t₁до t₂,

q= (c_m) (t₂ -t₁) = c_m2 t₂ - c_m1t₁, (4.5)
где c_m2 иc_m1– соответственно средние теплоемкости в пределах 0°-t₁ и 0°-t₂.

В таблице 4.2 приведены интерполяционные формулы для истинных и средних мольных теплоемкостей при постоянном давлении, а в таблице 4.3 – для средних массовых объемных теплоемкостей при постоянном объеме.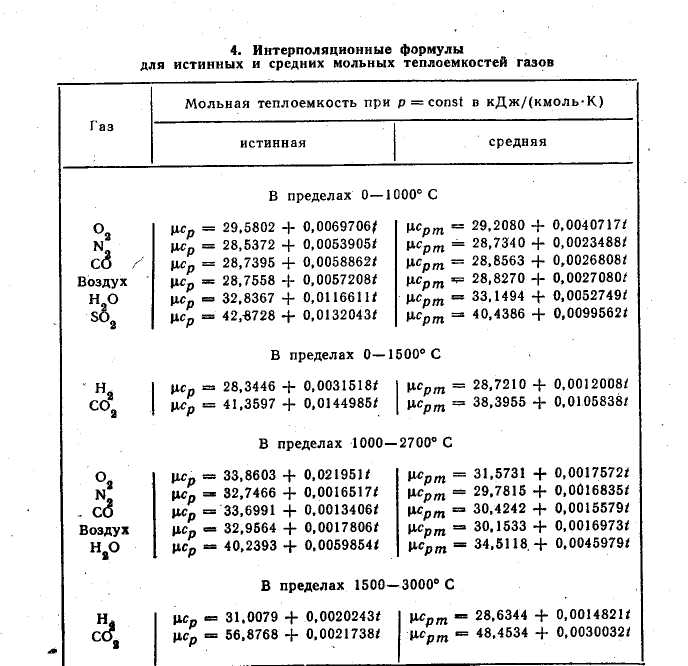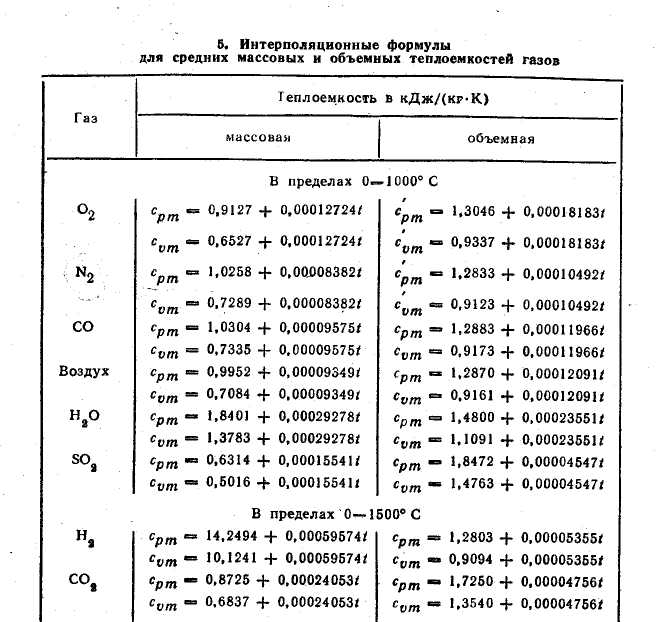






Теплоемкость газовой смеси

Массовая

с_см= (4.6)

Объемная

с^/_см= 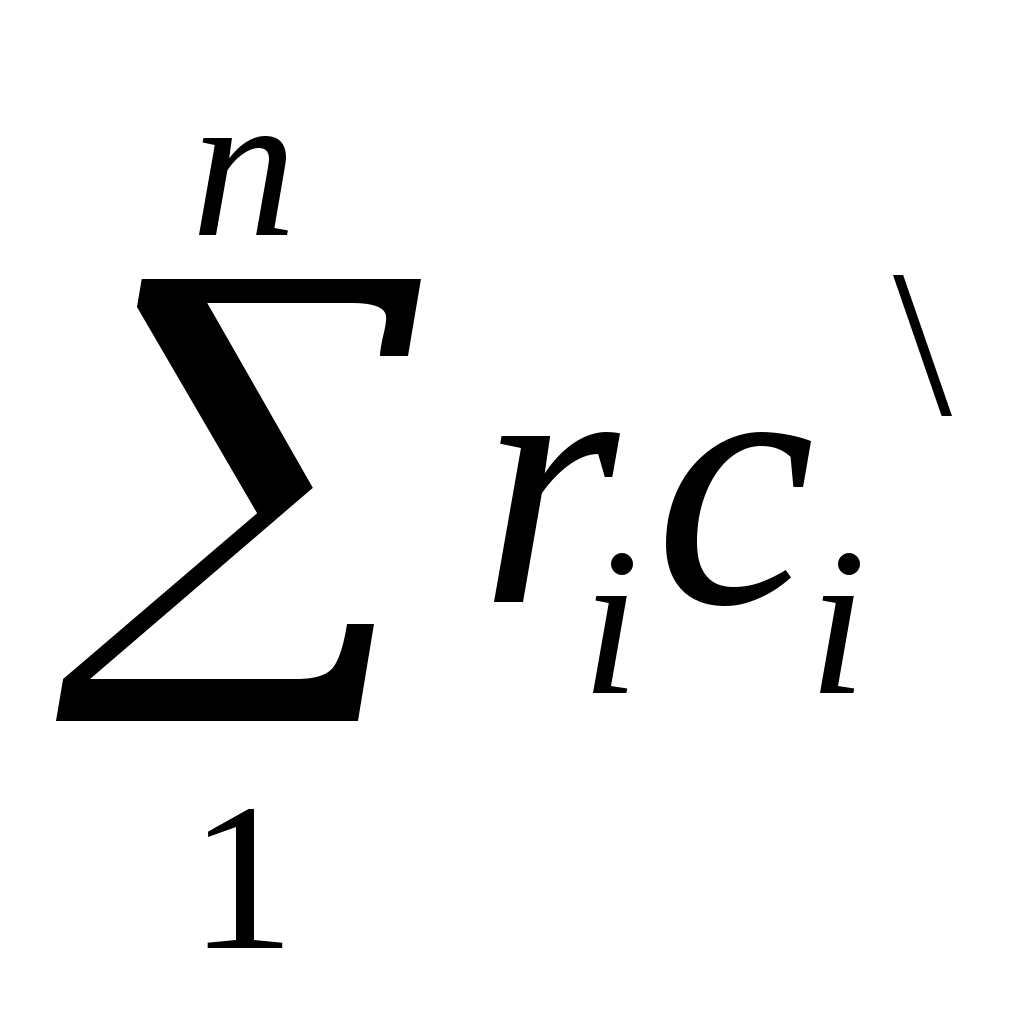(4.7)

мольная

μ c_см= (4.8

Задачи
4.1. Найти объемную теплоемкость кислорода при по­стоянном объеме и постоянном давлении, считая с = cоnst.
4.2. Определить значение массовой теплоемкости кислорода при постоянном объеме и постоянном давлении, считая с = cоnst.
4.3. Вычислить среднюю массовую и сpеднюю объемную теплоемкость окиси углерода при постоянном объеме для интeрвала температур 0-1200°C если известно, что для окиси углерода (µс_рm)₀¹²⁰⁰=32,192кДж/(кмоль • К).
4.4. Определить среднюю массовую теплоемкость угле­кислого газа при постоянном давлении в пределаx 0­-825^°С, считая зависимость от температуры нелинейной.
4.5. Вычислить значение истинной мольной теплоем­кости кислорода при постоянном давлении для температуры ­1000^°C, считая зависимость теплоемкости от тем­пературы линейной
4.6. Вычислить среднюю теплоемкость с_рт для воздуха при постоянном давлении в пределах 200-800^° C, считая зависимость теплоемкости от температуры нелинейной.
4.7. Вычислить среднюю теплоемкость с_рт для воздуха при постоянном давлении в пределах 200-800^° C, считая зависимость теплоемкости от температуры линейной.
4.8. Определить среднюю массовую теплоемкость с_рт для кислорода при постоянном давлении в пределах от 350-1000° C, считая зависимость теплоемкости от тем­пературы: а) нелинейной; 6) линейной.
4.9. Вычислить среднюю теплoемкость с_рm и с_vmв пределах 200-800^°С для СО, считая зависимость тепло­емкости от температуры линейной.
4.10. Найти среднюю теплоемкость с_рm и с_vmдля воздуха в пределах 400-1200^° C, считая зависимость теплоемкоcти от температуры нелинейной.
4.11. Найти среднюю теплоемкость с_рm и с_vmуглекис­лого газа в пределах 440- 1000^° C, считая зависимость теплоемкости от температуры нелинейной.
4.12. Определить среднюю массовую теплоемкость при постоянном объеме для азота в пределах 200-800°С, считая зависимость теплоемкости от температуры нели­нейной.
4.13. Воздух в количестве 6 м³ при давлении р₁ = 0,3 МПа и температуре t = 25° C нагревaeтся при постоянном давлении до t₂ = 130° C. Определить количество подведенной к воздуху теплоты, считая с = const.
4.14. В закрытом сосуде объемом V = 300 л находится воздух при давлении р₁ = 0,8 МПа и температуре t₁ = 20° С. Какое количество теплоты необходимо подвести, чтобы температyра воздуха поднялась до t = 120° С?

Задачу решить, принимая теплоемкость воздуха постоянной, а также учитывая зависимость теплоемкость теплоемкости от температуры.­

4.15. Воздух охлаждается от 1000 до 100° C в процессе c постоянным давлением. Какое количествo теплоты теряет 1 кг воздуха? Задачу решить, принимая теплоемкость воздуха постоянной, a также учитывая зависимость теплоемкоcти от темпе­ратуры.
4.16. B сосуде объемом 300 л нaходится кислopод при давлении р₁ = 0,2 МПа и температуре t₁ = 20° C. Какое количество теплоты необходимо подвести, чтобы

температура кислорода повысилась до t₂ = 300° C? Какое давление установится при этом в сосуде? Зависимость теплоемкости от температуры принять нелинейной.
4.17. Найти количество теплоты, необходимое для на­грева 1 м³ (при нормальных условиях) газовой смеси со­става гсо₂ = 14, 5 % , ro₂ = 6,5 % , r _{N 2} = 79,0 % от 200 до 1200^°С при р = const и нелинeйной зависимости тепло­емкости от температуры.
4.18. Газовая смесь имеет следующий состав по объему:

СО ₂ = 0,12; O ₂ = 0, 07; N _z = 0, 75; Н₂0 = 0,06.Определить сpеднюю массовую теплоемкость с_рт,если смесь нaгревается от 100 до 300° C.
4.19. B регенеративном подогревателе газовой турбины воздух нагревается от 150 до 600° C. Найти количество теплоты, сообщенное воздуху в еди­ницу времeни, если расход его составляет. 360 кг/ч. За­висимость теплоемкoсти от темпеpатуры принять нели­нейной

4.20. Продукты сгорания топлива поступают в газоход парового котла при температуре газов t_г ^'= 1100° C и покидают газоход пpи темпера­туре t₂ ' ^'= 700° C. Состaв газов по объему: rco₂ = 11 % ; ro₂ = 6%; гн₂о = 8%.; г _N2 = 75%.

Определить, какое количе­ство теплоты теряет 1 м³ газовой смеси, взятой при нормальных условиях.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5.