Перегудов Ф. И., Тарасенко Ф. П
 Скачать 4.17 Mb.
|
§ 5.7. КОЛИЧЕСТВО ИНФОРМАЦИИВ основе всей теории информации лежит открытие, что информация допускает количественную оценку. В простейшей форме эта идея была выдвинута еще в 1928 г. Хартли, но завершенный и общий вид придал ей Шэннон в 1948 г. [9]. Не останавливаясь на том, как развивалось и обобщалось понятие количества информации, дадим сразу его современное толкование. КОЛИЧЕСТВО ИНФОРМАЦИИ КАК МЕРА СНЯТОЙ НЕОПРЕДЕЛЕННОСТИ Процесс получения информации можно интерпретировать как изменение неопределенности в результате приема сигнала. Проиллюстрируем эту идею на примере достаточно простого случая, когда передача сигнала происходит при следующих условиях: 1) полезный (отправляемый) сигнал является последовательностью статистически независимых символов с вероятностями р(хi),  ; 2) принимаемый сигнал является последовательностью символов уk того же алфавита; 3) если шумы (искажения) отсутствуют, то принимаемый сигнал совпадает с отправляемым уk = хi; 4) если шум имеется, то его действие приводит к тому, что данный символ может либо остаться прежним (i-м), либо быть подмененным любым другим (k-м) символом, вероятность этого равна р(уk | хi); 5) искажение очередного символа является событием, статистически независимым от того, что произошло с предыдущими символами. Конечно, можно рассматривать ситуацию и со стороны передатчика, используя вероятности р(хi | уk) (рис. 5.4). В этих условиях энтропия процесса есть энтропия одного символа, и все сводится к рассмотрению посимвольного приема. Итак, до получения очередного символа ситуация характеризуется неопределенностью того, какой символ будет отправлен, т.е. априорной энтропией Н(Х). После получения символа уk неопределенность относительно того, какой символ был отправлен, меняется: в случае отсутствия шума она вообще исчезает (апостериорная энтропия равна нулю, поскольку точно известно, что был передан символ хk = уk), а при наличии шума мы не можем быть уверены, что полученный нами символ и есть отправленный, и возникает неопределенность, характеризуемая апостериорной энтропией Н(Х | уk) = Н({р(хi | уk)}) > 0. В среднем после получения очередного символа энтропия Н(Х | Y) = MyН(Х | уk). Определим теперь количество информации как меру снятой неопределенности: числовое значение количества информации о некотором объекте равно разности априорной и апостериорной энтропий этого объекта, т.е. I(Х, Y) = Н(Х) – Н(X | Y). (1) Использовав равенство (2) § 5.6, легко получить, что I(Х, Y) =Н(Y) – Н(Y | Х). (2) В явной форме равенство (1) запишется так: 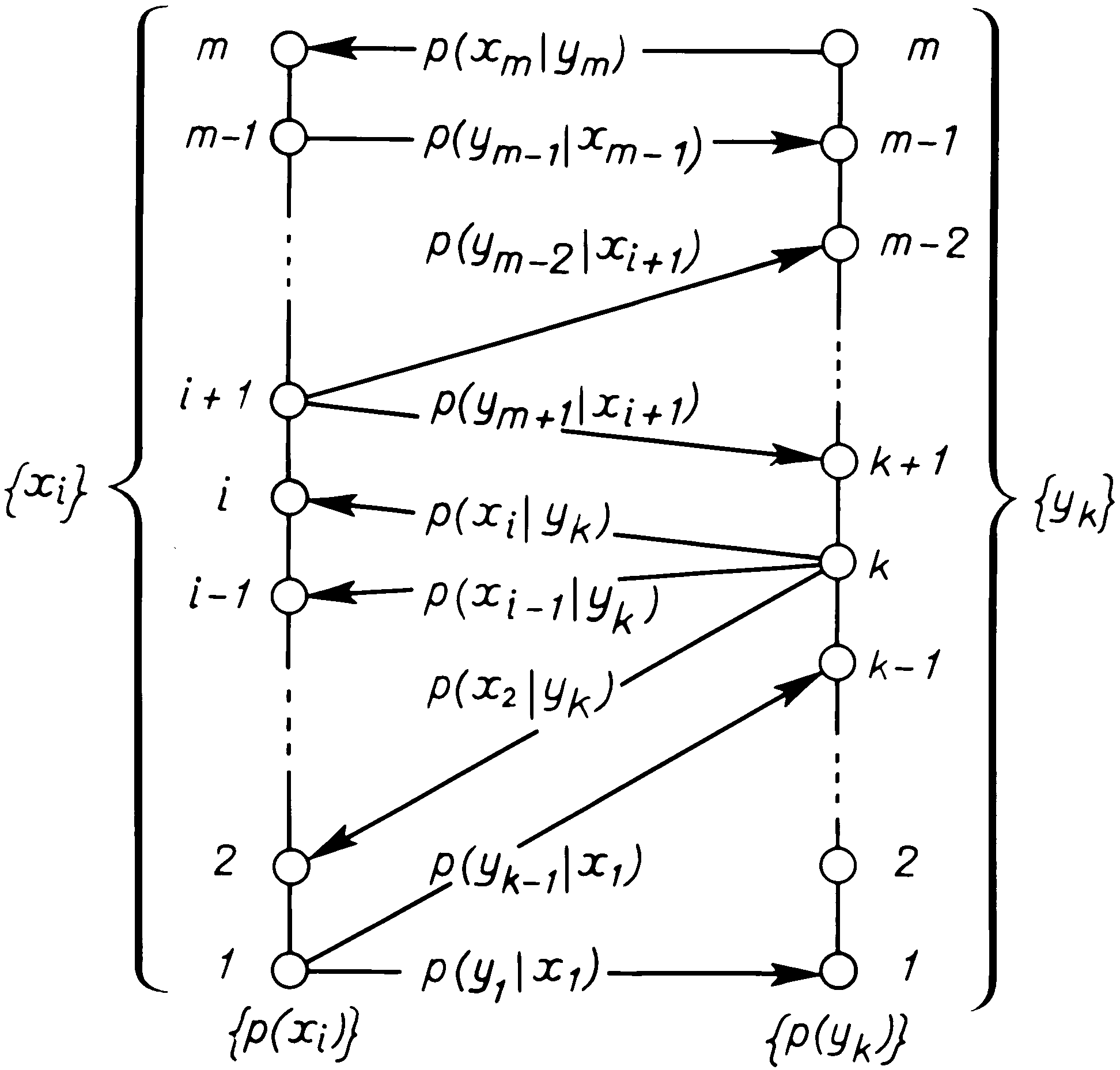 5.4 ————— Схема “вееров неопределенности” при наличии шума в канале  (3)а для равенства (2) имеем  (4)КОЛИЧЕСТВО ИНФОРМАЦИИ КАК МЕРА СООТВЕТСТВИЯ СЛУЧАЙНЫХ ОБЪЕКТОВ Этим формулам легко придать полную симметричность: умножив и разделив логарифмируемое выражение в (3) на р(уk), а в (4) на р(хi), сразу получим, что  (5)Эту симметрию можно интерпретировать так: количество информации в объекте Х об объекте Y равно количеству информации в объекте Y об объекте Х. Таким образом, количество информации является не характеристикой одного из объектов, а характеристикой их связи, соответствия между их состояниями. Подчеркивая это, можно сформулировать еще одно определение: среднее количество информации, вычисляемое по формуле (5), есть мера соответствия двух случайных объектов. Это определение позволяет прояснить связь понятий информации и количества информации. Информация есть отражение одного объекта другим, проявляющееся в соответствии их состояний. Один объект может быть отражен с помощью нескольких других, часто какими-то лучше, чем остальными. Среднее количество информации и есть числовая характеристика степени отражения, степени соответствия. Подчеркнем, что при таком описании как отражаемый, так и отражающий объекты выступают совершенно равноправно. С одной стороны, это подчеркивает обоюдность отражения: каждый из них содержит информацию друг о друге. Это представляется естественным, поскольку отражение есть результат взаимодействия, т.е. взаимного, обоюдного изменения состояний. С другой стороны, фактически одно явление (или объект) всегда выступает как причина, другой – как следствие; это никак не учитывается при введенном количественном описании информации. Формула (5) обобщается на непрерывные случайные величины, если в соотношения (1) и (2) вместо Н подставить дифференциальную энтропию h; при этом исчезает зависимость от стандарта Е и, значит, количество информации в непрерывном случае является столь же безотносительным к единицам измерения, как и в дискретном:  (6)где р(х), р(y) и р(х, y) – соответствующие плотности вероятностей. Свойства КОЛИЧЕСТВА ИНФОРМАЦИИ Отметим некоторые важные свойства количества информации. 10. Количество информации в случайном объекте Х относительно объекта Y равно количеству информации в Y относительно Х: I(Х, Y) = I(Y, Х). (7) 20. Количество информации неотрицательно: I(Х, Y) 0. (8) Это можно доказать по-разному. Например, варьированием р(х, y) при фиксированных р(х) и р(y) можно показать, что минимум I, равный нулю, достигается при р(х, у) = p(х)p(y). 30. Для дискретных Х справедливо равенство I(Х, Х) = Н(Х). 40. Преобразование ?(·) одной случайной величины не может увеличить содержание в ней информации о другой, связанной с ней, величине: I(? (Х), Y) I(Х, Y) (9) 50. Для независимых пар величин количество информации аддитивно: I({Xi, Yi}) =  I(Xi, Yi). (10) INTERACTION взаимодействие DISTORTION искажение QUANTITY количество DENSITY плотность AVERAGE средний Количество информации можно определить как меру уменьшения неопределенности в результате получения сигнала. Это соответствует разности энтропий до и после приема сигнала. Среди свойств количества информации выделяются следующие: 1) количество информации (в отличие от энтропии) имеет одинаковый смысл как для дискретных, так и для непрерывных случайных объектов; 2) при обработке данных содержащееся в них количество информации не может быть увеличено. Следовательно, обработка делается лишь для представления информации в более удобном, компактном виде и в лучшем случае без потери полезной информации. ЕДИНИЦЫ ИЗМЕРЕНИЯ ЭНТРОПИИ И КОЛИЧЕСТВА ИНФОРМАЦИИ Рассмотрим теперь вопрос о единицах измерения количества информации и энтропии. Из определений I и Н следует их безразмерность, а из линейности их связи – одинаковость их единиц. Поэтому будем для определенности говорить об энтропии. Начнем с дискретного случая. За единицу энтропии примем неопределенность случайного объекта, такого, что  . (11)Легко установить, что для однозначного определения единицы измерения энтропии необходимо конкретизировать число m состояний объекта и основание логарифма. Возьмем для определенности наименьшее число возможных состояний, при котором объект еще остается случайным, т.е. m = 2, и в качестве основания логарифма также возьмем число 2. Тогда из равенства –р1log2р1 – р2log2р2 = 1 вытекает, что р1 = р2 = 1/2. Следовательно, единицей неопределенности служит энтропия объекта с двумя равновероятными состояниями. Эта единица получила название “бит”. Бросание монеты дает количество информации в один бит. Другая единица (“нит”) получается, если использовать натуральные логарифмы, обычно она употребляется для непрерывных величин. КОЛИЧЕСТВО ИНФОРМАЦИИ В ИНДИВИДУАЛЬНЫХ СОБЫТИЯХ Остановимся еще на одном важном моменте. До сих пор речь шла о среднем количестве информации, приходящемся на любую пару состояний (хi, уk) объектов Х и Y. Эта характеристика естественна для рассмотрения особенностей стационарно функционирующих систем, когда в процессе функционирования (рано или поздно, реже или чаще) принимают участие все возможные пары (хi, уk). Однако в ряде практических случаев оказывается необходимым рассмотреть информационное описание конкретной пары состояний, оценить содержание информации в конкретной реализации сигнала. Тот факт, что некоторые сигналы несут информации намного больше, чем другие, виден на примере того, как отбираются новости средствами массовой информации (скажем, все радиостанции и газеты сообщают о рождении шестерых близнецов где-то в Южной Америке, но о рождении двойни обычно не пишут). Допуская существование количественной меры информации i(хi, уk) в конкретной паре (хi, уk), естественно потребовать, чтобы индивидуальное и среднее количества информации удовлетворяли соотношению  . (12) Хотя равенство сумм имеет место не только при равенстве всех слагаемых, сравнение формул (12) и, например, (4) наталкивает на мысль, что мерой индивидуальной информации в дискретном случае может служить величина  , (13) а в непрерывном – величина  , (14) называемая информационной плотностью. Свойства этих величин согласуются с интуитивными представлениями (в том числе и возможная отрицательность при положительности в среднем) и, кроме того, доказана единственность меры, обладающей указанными свойствами. Полезность введения понятия индивидуального количества информации проиллюстрируем на следующем примере. Пусть по выборке (т.е. совокупности наблюдений) х = х1, ..., хN требуется отдать предпочтение одной из конкурирующих гипотез (Н1 или Н0), если известны распределения наблюдений при каждой из них, т.е. р(х | Н0) и р(х | Н1). Как обработать выборку? Из теории известно, что никакая обработка не может увеличить количества информации, содержащегося в выборке х (см. формулу (9)). Следовательно, выборке х нужно поставить в соответствие число, содержащее всю полезную информацию, т.е. обработать выборку без потерь. Возникает мысль о том, чтобы вычислить индивидуальные количества информации в выборке х о каждой из гипотез и сравнить их:  . (15)Какой из гипотез отдать предпочтение, зависит теперь от величины ?i и от того, какой порог сравнения мы назначим. Оказывается, что мы получили статистическую процедуру, оптимальность которой специально доказывается в математической статистике, – именно к этому сводится содержание фундаментальной леммы Неймана – Пирсона. Данный пример иллюстрирует эвристическую силу теоретико-информационных представлений.
|