Перегудов Ф. И., Тарасенко Ф. П
 Скачать 4.17 Mb. Скачать 4.17 Mb.
|
§ 7.12. ВЫБОР И ОТБОРДо настоящего параграфа речь шла о процедурах одноразового выбора. Даже тогда, когда приходилось проводить выбор в несколько этапов (многокритериальная оптимизация, коллективный выбор, метод “Делфи” и т.д.), это были этапы промежуточные, подготовительные перед последним, окончательным выбором. ПОВТОРНЫЙ ВЫБОР Однако возможны ситуации, в которых выбор повторяется многократно, причем каждый последующий выбор происходит в условиях, отличающихся от тех, в которых происходил предыдущий. Это придает динамику самому процессу выбора и его последствиям. Конкретный характер происходящих при этом изменений зависит от многих факторов: самой природы множества альтернатив, степени влияния предыдущего выбора на последующий, от того, насколько и как именно учитываются происшедшие изменения на очередном шаге выбора, и т.д. При этом возможные постановки задач весьма разнообразны, но очень немногие из этих задач на сегодняшний день рассмотрены. Наиболее подробно изучены процессы принятия статистических решений с адаптацией, т.е. с обратной связью по решениям, иначе говоря, принятие решения на очередном шаге с учетом решений, принятых на предыдущих шагах. Примером могут служить радиолокационные станции, постоянно ведущие обзор заданной зоны, накапливающие информацию о помеховой обстановке в зоне обзора и использующие эту информацию при обработке принятых сигналов для обнаружения целей. Главный результат состоит в том, что такая адаптация может улучшить качество решений. Другой пример процессов многократного выбора дает естественный отбор. Своеобразие таких процессов изучается теорией эволюции, математической биологией. Для нас основной интерес представляют процессы сознательного выбора, поэтому, обращаясь к многократному выбору, мы приходим, в частности, к задачам целенаправленного многократного выбора, т.е. искусственного отбора, селекции. Как показали исследования А.Н. Ефимова и В.М. Кутеева, тенденции, возникающие в ходе селекции, сильно зависят от конкретных способов формирования и пополнения отборных (“элитных”) групп. Даже простейшие модели селекции обнаруживают интересные эффекты в эволюции элитных групп [14; 15]. Эти эффекты следует иметь в виду при комплектовании любых групп элементов, в чем-то лучших, чем остальные: в промышленности – при изготовлении высокосортной продукции; в сельском хозяйстве – при выводе высокопроизводительных пород животных и сортов растений; в управленческой деятельности – при комплектовании групп исполнителей особо ответственных дел и т.д. ОСНОВНЫЕ ИДЕИ ТЕОРИИ ЭЛИТНЫХ ГРУПП Рассмотрим модель, предложенную А.Н. Ефимовым*. Предположим, что имеется некоторая совокупность элементов. Пусть интересующее нас свойство элемента выражается некоторой критериальной величиной x; для определенности будем считать, что чем больше значение x, тем лучше, и что 0x1. В исходной совокупности присутствуют элементы с любыми значениями величины x, и задача отбора возникает, если для достижения некоторой цели потребуется, чтобы показатель качества был не ниже некоторой заданной величины a<1. Предположим, что из исходной совокупности с помощью определенного эталона (носителя величины a) отбирается заданное количество n элементов. Для общности можно предположить, что процедура отбора изредка дает сбои, так что в элитную группу с небольшой вероятностью ? попадают и “сорные” элементы, для которых x a. С некоторым количеством “сорных” элементов или без них, но элитная группа сформирована и может приступить к выполнению стоящей перед ней задачи. Если элементы для отбора выбираются случайно, F(x) – функция распределения качества x в исходной группе, f(x) – соответствующая ей плотность, то распределение качества x в сформированной элитной группе характеризуется плотностью Очевидно, что среднее качествоxэ элитной группы зависит от величин ? и F(a). Так как обычно ? достаточно мало, а F(a) достаточно велико, т.е. ? < F(a), тоxэ >x. При ? = F(a) среднее качество “элиты” не отличается от среднего качества всей совокупности, a при ? > F(a) становится хуже него (эти случаи не представляют практического интереса). Если в силу любых причин (старения, разрушения, изъятия, отчисления, смерти и т.д.) какие-то элементы выбывают из элитной группы, а ее численность требуется сохранить, то возникает задача повторного выбора элементов из оставшейся основной совокупности в состав элитной группы. Ответ на вопрос, как будут изменяться свойства элитной группы при многократном повторении этого действия, зависит от ряда обстоятельств и может быть различным. Главные факторы, очевидно, таковы: доля элитной группы в совокупности элементов, хотя и отвечающих требованиям элитности, но оставшихся вне элиты (если в первичную элитную группу вошли все элементы, для которых x > a, то ее придется пополнять за счет элементов, для которых x a ); характер изменения качества x каждого элемента со временем не только в элитной группе, но и в остальной совокупности (оно может как оставаться постоянным, так и изменяться); правило отсева из элитной группы (происходит ли это случайно, без учета величины x, либо выбывают лучшие или худшие элементы); правило включения новых элементов в элитную группу (в соответствии с прежним эталоном a либо с измененным эталоном, либо при невозможности дальнейшего использования эталона после первого отбора); временные отношения между моментами очередных пополнений элитной группы (эти отношения становятся важными при изменении качества x у элементов со временем). Различные сочетания этих условий приводят к возникновению большого количества задач, приводящих к разным типам эволюции качества элитной группы. Рассмотрим некоторые из них. Во всех случаях будем считать, что выделение элитной группы практически не сказывается на свойствах оставшейся совокупности (математически это соответствует, например, конечной численности элитной группы и несчетности исходной совокупности, что позволяет считать распределение F(x) неизменным при выделении элитных элементов). ПРОЦЕДУРА “ПРЕТЕНДЕНТ – РЕКОМЕНДАТЕЛЬ” В качестве первой задачи рассмотрим правило “претендент – рекомендатель”. Это правило состоит в том, что при наличии вакансии в элите взятый наугад из общей совокупности элемент (“претендент”) сравнивается с наугад взятым из элиты элементом (“рекомендателем”); если значение x у претендента не меньше, чем у рекомендателя, то претендент становится членом элиты; если меньше, то образуется новая пара “претендент – рекомендатель”. В этом случае направление изменения качества элитной группы определяется тем, какие элементы (худшие или лучшие) дольше существуют в группе. Если дольше “живут” худшие (как шарик в подшипнике, имеющий наименьший диаметр), то элитная группа неминуемо деградирует, поскольку худшие чаще выступают как рекомендатели. Наоборот, при увеличении времени T(x) жизни элемента с ростом величины x худшие элементы выбывают в первую очередь, в рекомендатели чаще попадают элементы повышенного качества, что приводит к непрерывному росту среднего качества элитной группы. При некоторых ограничениях на временные интервалы между заменами существуют невырожденные предельные распределения качества x в элитной группе. ПРОЦЕДУРЫ “ПРОПОЛКА” И “СНЯТИЕ УРОЖАЯ” Рассмотрим теперь вторую задачу – правило “прополка”. Оно состоит в удалении из элитной группы m наихудших элементов и замене их взятыми наугад m элементами из основной группы. При этом в элиту могут попасть как элементы лучшие, чем удаленные при прополке, так и худшие. Однако на следующем шаге прополки снова удаляются m худших элементов элитной группы, так что при m < n худшие в элите не задерживаются, а лучшие из новых остаются. В результате элитная группа прогрессирует, ее распределение Fkэ(x|m, n) с ростом числа прополок k сходится к некоторому предельному распределению Fэ(x|m, n), зависящему от величины m, 0 < m <n. Интересно, что наилучшая стратегия прополки, дающая наивысшее предельное среднее качество элитной группы, состоит в удалении из элитной группы только одного наихудшего элемента на каждом шаге. Процедуру, обратную “прополке”, когда из группы удаляются t наилучших элементов, А.Н. Ефимов называет правилом “снятия урожая”. При этом эффекты противоположны тем, которые мы наблюдали при прополке: наибольший вред группе приносит удаление на каждом шаге только одного наилучшего элемента. Процедура “претендент – рекомендатель” реализует в некотором смысле одинаковое обращение с исходной совокупностью и с элитной группой. Процедуры “прополка” и “снятие урожая” предполагают основную активность внутри элитной группы. ПРОЦЕДУРА “ДЕЛЕГИРОВАНИЕ” Рассмотрим теперь возможность внешней активности в формировании элиты. Вариант такой процедуры, называемой правилом “делегирования”, состоит в следующем: 1) из исходной совокупности случайным образом выбирают N элементов – делегирующую выборку; 2) делегирующую выборку упорядочивают по величине x; 3) элемент с наибольшим рангом зачисляют в формируемую элитную группу. На этапе формирования элитной группы процедуру повторяют n раз – столько, сколько вакансий должно быть заполнено. С помощью теории порядковых статистик удается связать величины a, ? и N: т.е. чем выше требования к качеству элитной группы, тем больше должен быть объем делегирующей выборки. Принципиальное отличие “делегирования” от процедуры “претендент – рекомендатель” состоит в отказе от сравнения делегатов с членами элиты. Далее, оказывается, что “делегирование” не только позволяет сформировать элиту любого нужного качества, но и предохранить элитную группу от деградации даже при большей жизнеспособности плохих элементов. Результаты решения приведенных задач имеют некоторые аналогии в общественных процессах. Однако рассмотренные модели слишком просты, чтобы можно было говорить о количественной теории социальных систем. А.Н. Ефимов пишет [13]: “Во-первых, такую теорию еще неплохо было бы создать объединенными усилиями социологов, экономистов, юристов и математиков. Пока что есть лишь несколько простейших моделей. Их анализ показывает, что построение элитных групп, не подверженных деградации, в принципе возможно. Это – во-вторых, и это вселяет надежды”.
ЗАКЛЮЧЕНИЕ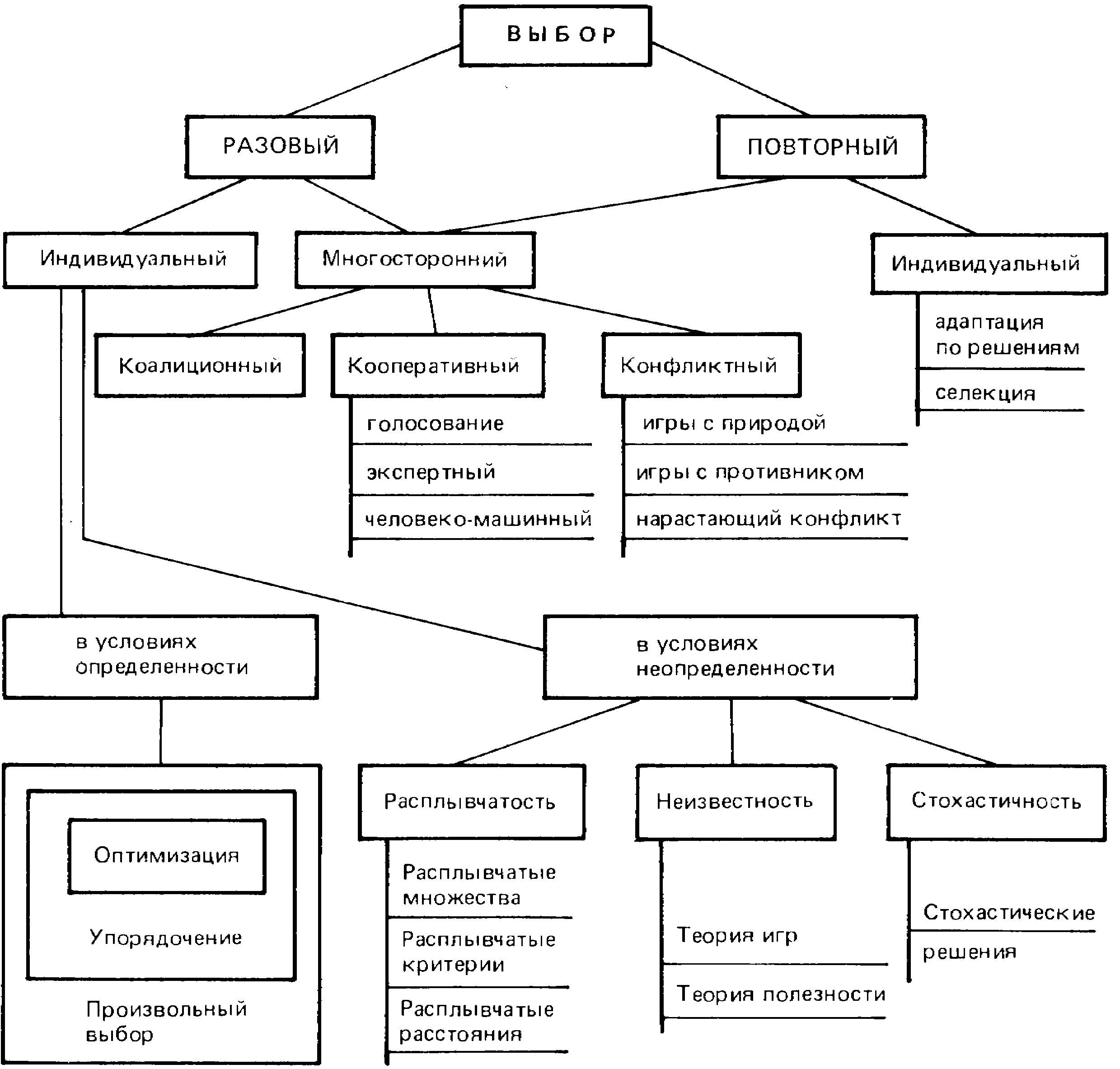 7.9 ————— Взаимосвязь задач выбора, рассмотренных в гл.7 На рис. 7.9 приведена схема, на которой изображены все упомянутые в данной главе задачи выбора, указаны их общность и различия в иерархической классификации. Кроме наглядности взаимосвязи этих задач схема выявляет тот факт, что большое количество задач осталось вообще нерассмотренным, поскольку иерархия далеко не полная. Причины того, что те или иные задачи не вошли в схему, могут быть различными. ЛИТЕРАТУРА
УПРАЖНЕНИЯ7.1
§ 7.2
§ 7.3
§ 7.4
§ 7.5
§ 7.6
§ 7.7
§ 7.8
§ 7.9
§ 7.10
§ 7.11
§ 7.12
Вопросы для самопроверки1. Что значит “сделать выбор”? 2. В чем главные отличия в описании выбора на трех языках: критериальном, бинарных отношений, функций выбора? 3. Почему разные постановки задачи многокритериального выбора приводят в общем случае к различным решениям? 4. Как определяется оптимальность по отношению R? 5. В чем заключается парадокс Эрроу? 6. При каких условиях меньшинство может навязать свою волю, несмотря на принятие решений большинством голосов? 7. Что позволяет выбор в условиях неопределенности исхода рассматривать как игру? 8. На каком множестве осуществляется выбор в случае статистической неопределенности? 9 Каковы основные правила статистической “техники безопасности”? 10. Как решается задача выбора при расплывчатой неопределенности, если критериальные функции отождествляются с функциями принадлежности? 11. Какие причины сужают возможности оптимизации в решении реальных проблем? 12. Какие факторы влияют на работу экспертов? 13. Какими достоинствами обладают человеко-машинные способы выбора? 14. Почему элитная группа может деградировать?
|
