2. книга по теории ДВС 09. 2012. 2. книга по теории ДВС 09. Первый и второй законы термодинамики
 Скачать 18.02 Mb.
|
|
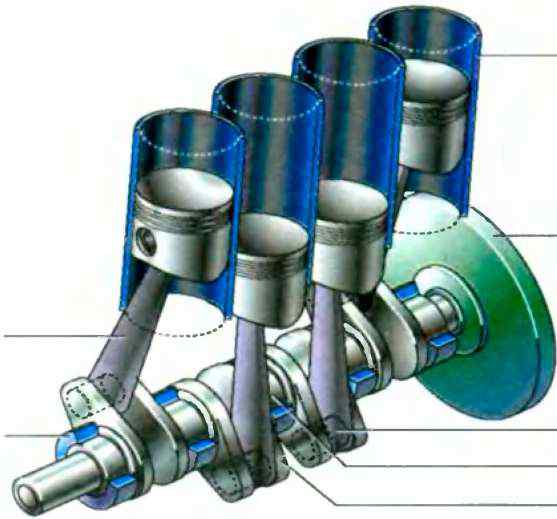С  илы , действующие в кривошипно-шатунном механизмеРасположение кривошипов вала зависит от числа и расположения цилиндров двигателя с учетом обеспечения равномерности чередования рабочих тактов. Кривошипы вала располагают под определенным углом, который для четырехтактных двигателей определяется отношением: а = (720°) \ Z, 360\z---для 2-хтактных двс где Z— число цилиндров двигателя. Например для 6-цилиндрового 4-х тактного ДВС угол заклинки мотылей (кривошипов) будет 720 \ 6 = 120 град При работе двигателя в КШМ каждого цилиндра действуют силы:
С 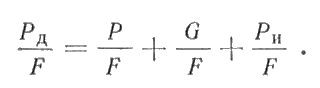 илы трения не поддаются точному расчету; их считают включенными в сопротивление гребного винта и не принимают во внимание. Следовательно, в общем случае на поршень действует движущая сила Pд = Р + G + Pи.Силы, отнесенные к 1 м2 площади поршня, 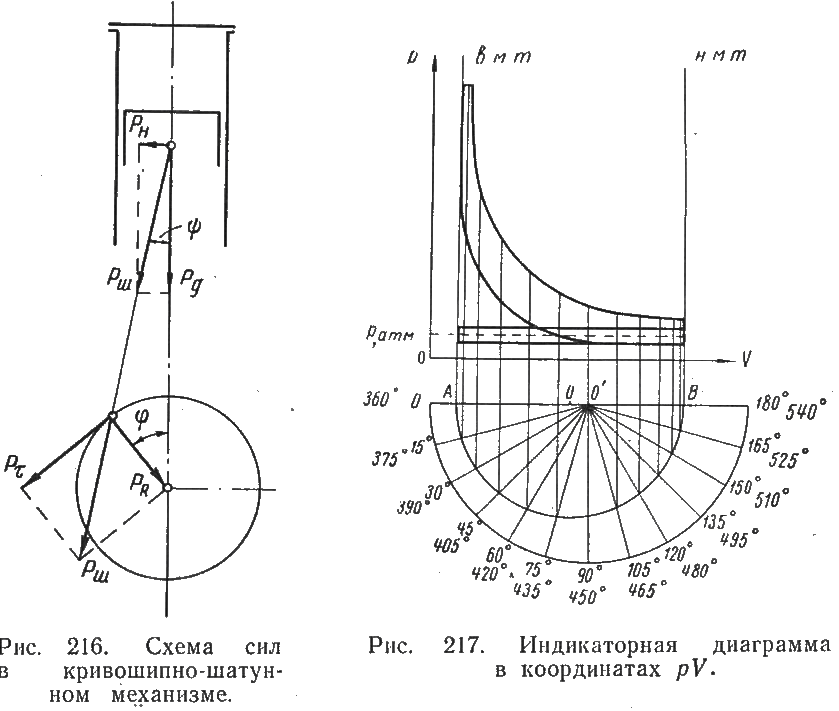 Движущее усилие Рд приложено к центру поршневого пальца (пальца крейцкопфа) и направлено вдоль оси цилиндра (рис. 216). На пальце поршня Pд раскладывается на составляющие: Рн — нормальное давление, действующее перпендикулярно к оси цилиндра и прижимающее поршень к втулке; Рш - усилие, действующее вдоль оси шатуна и передаваемое на ось шейки кривошипа, где оно в свою очередь раскладывается на составляющие Рτ и РR (рис. 216). Усилие Рτ действует перпендикулярно к кривошипу, вызывает его вращение и называется касательным. Усилие РR действует вдоль кривошипа и называется радиальным. Из геометрических соотношений имеем: 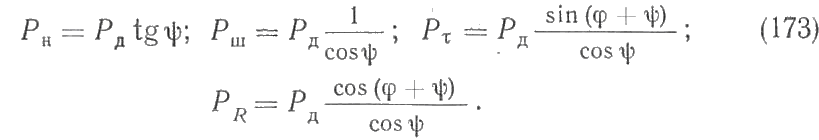 Численное значение и знак тригонометрических величин 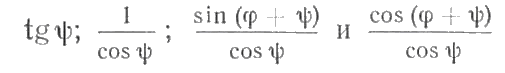 для двигателей с различными постоянными КШМ λ =R / L можно принять по данным Величину и знак Рд определяют из диаграммы движущих сил, представляющей графическое изображение закона изменения движущей силы за один оборот коленчатого вала для двухтактных двигателей и за два оборота для четырехтактных в зависимости от угла поворота коленчатого вала. Чтобы получить значение движущей силы, необходимо предварительно построить следующие три диаграммы. 1  . Диаграмма изменения давления р в цилиндре в зависимости от угла поворота кривошипа φ. По данным расчета рабочего процесса двигателя строят теоретическую индикаторную диаграмму, по которой определяют давление в цилиндре р в зависимости от его объема V. Для того, чтобы перестроить индикаторную диаграмму из координат рV в координаты р—φ (давление — угол поворота вала), линии в. м. т. и н. м. т. следует продлить вниз и провести прямую АВ, параллельную оси V (рис. 217). Отрезок АВ делится точкой О пополам и из этой точки радиусом АО описывается окружность. От центра окружности точки О в сторону н. м. т. откладывают отрезок OO' = 1 / 2 R2 / L поправка Брикса. Так какЗначение постоянной КШМ λ = R / L принимают по опытным данным. Чтобы получить величину поправки OO', в масштабе диаграммы в формулу OO' = 1 / 2 λR вместо R подставляют значение отрезка АО. Из точки О', которая называется полюсом Брикса, описывают произвольным радиусом вторую окружность и делят ее на любое число равных частей (обычно через каждые 15°). Из полюса Брикса О' через точки деления проводят лучи. Из точек пересечения лучей с окружностью радиусом АО проводят вверх прямые, параллельные оси р. Затем на свободном месте чертежа строят с помощью измерителя координаты давления газов р — угол поворота кривошипа φ°; принимая за начало отсчета линию атмосферного давления, снимают с диаграммы р—V значения ординат процессов наполнения и расширения для углов 0°, 15°, 30°, …, 180° и 360°, 375°, 390°, ..., 540°, переносят их в координаты для этих же углов и соединяют полученные точки плавной кривой. Аналогично строят участки сжатия и выпуска, но в этом случае поправку Брикса ОО' откладывают на отрезке АВ в сторону в. м. т. В результате указанных построений получают развернутую индикаторную диаграмму (рис. 218, а), по которой можно определить давление газов р на поршень для любого угла φ поворота кривошипа. Масштаб давлений развернутой диаграммы будет такой же, как и на диаграмме в координатах р—V. При построении диаграммы p = f(φ) силы, способствующие движению поршня, считаются положительными, а силы, препятствующие этому движению,— отрицательными. 2 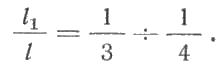 . Диаграмма сил массы возвратно-поступательно-движущихся частей КШМ. В тронковых двигателях внутреннего сгорания масса поступательно-движущихся частей включает массу поршня и часть массы шатуна. В крейцкопфных дополнительно входят массы штока и ползуна. Массу частей можно подсчитать, если имеются чертежи с размерами этих деталей. Часть массы шатуна, совершающая возвратно-поступательное движение, G1 = Gш l1 / l, где Gш— масса шатуна, кг; l — длина шатуна, м; l1 — расстояние от центра тяжести шатуна до оси кривошипной шейки, м: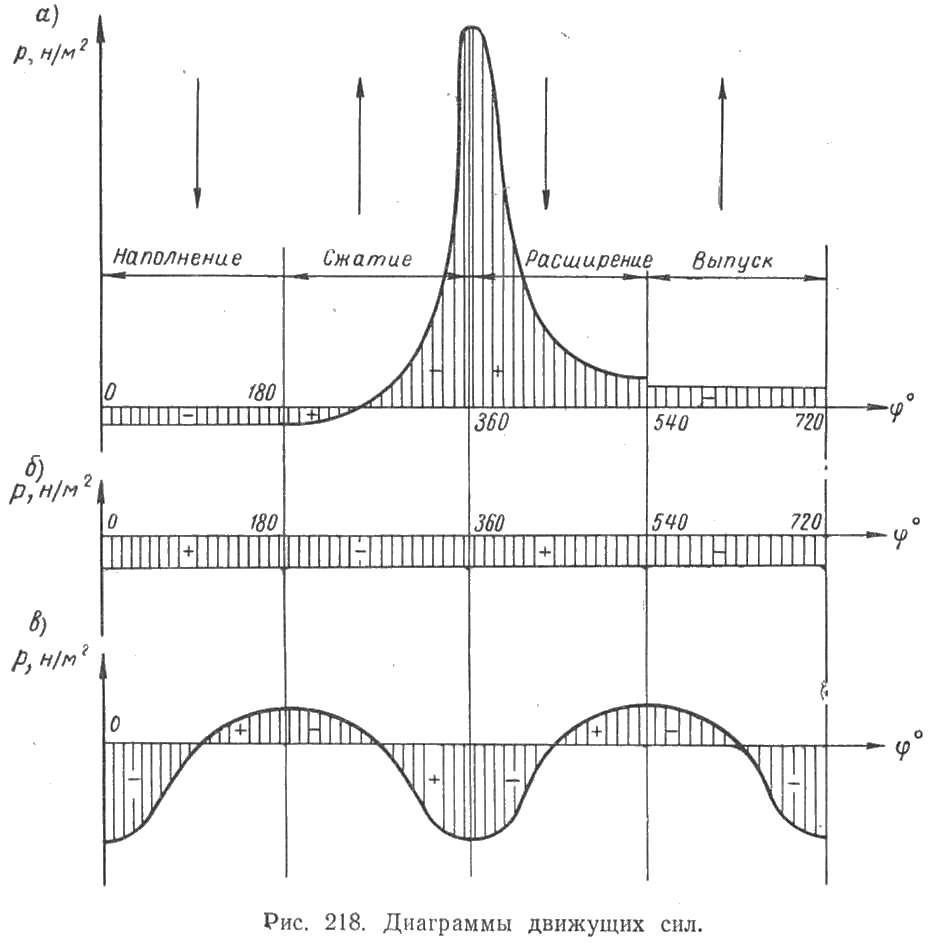 Развернутая диаграмма сил от давления газов. Диаграмма удельных сил масс поступательно движущихся частей. Диаграмма сил инерции поступательно-движущихся частей одного цилиндра. Для предварительных расчетов удельные значения массы поступательно-движущихся частей могут быть приняты: 1) для тронковых быстроходных четырехтактных двигателей 300—800 кг/м2 и тихоходных 1000—3000 кг/м2; 2) для тронковых быстроходных двухтактных двигателей 400—1000 кг/м2 и тихоходных 1000— 2500 кг/м2; 3) для крейцкопфных быстроходных четырехтактных двигателей 3500—5000 кг/м2 и тихоходных 5000—8000 кг/м2; для крейцкопфных быстроходных двухтактных двигателей 2000—3000 кг/м2 и тихоходных 9000—10 000 кг/м2. Так как величина массы поступательно-движущихся частей КШМ и их направление не зависят от угла поворота кривошипа φ, то диаграмма сил массы будет иметь вид, показанный на рис. 218, б. Строится эта диаграмма в том же масштабе, что и предыдущая. На тех участках диаграммы, где сила массы способствует движению поршня, она считается положительной, а там, где препятствует,— отрицательной 3. Диаграмма сил инерции поступательно-движущихся частей. Известно, что сила инерции поступательно-движущегося тела Ри =Gaн (G — масса тела, кг; а — ускорение, м/сек2). Масса поступательно-движущихся частей КШМ, отнесенная к 1 м2 площади поршня, m = G / F. Ускорение движения этой массы определяют по формуле (172). (Формула силы инерции Ри =-мп а , где а = - Rω2(cоsа + R/Lcos 2а) – ускорение поршня.) Таким образом, сила инерции поступательно-движущихся частей КШМ, отнесенная к 1 м2 площади поршня, может быть определена для любого угла поворота кривошипа по формуле 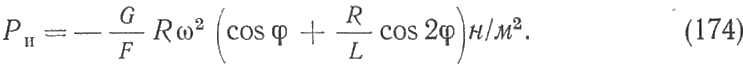 Расчет Ри для различных φ целесообразно производить в табличной форме. По данным таблицы строят диаграмму сил инерции поступательно-движущихся частей в том же масштабе, что и предыдущие. Характер кривой Pи= f (φ) дан на рис. 218, в. В начале каждого хода поршня силы инерции препятствуют его движению. Поэтому силы Ри имеют отрицательный знак. В конце же каждого хода силы инерции Ри способствуют этому движению и поэтому приобретают положительное значение. ОТВЕТИТЬ НА ВОПРОСЫ: 1. КАК ОПРЕДЕЛЯЕТСЯ СИЛА ДАВЛЕНИЯ ГАЗОВ НА ПОРШЕНЬ. 2. КАКАЯ СИЛА (РИС.216) ИЗНАШИВАЕТ ВТУЛКУ ЦИЛИНДРОВ. 3. КАК ОПРЕДЕЛИТЬ УГОЛ ЗАКЛИНКИ МОТЫЛЕЙ КОЛЕНВАЛА. 4. КАКАЯ СИЛА (РИС.216) ИЗНАШИВАЕТ ШЕЙКИ КОЛЕНВАЛА И ВКЛАДЫШИ. 5. ПРИ КАКОМ ПОЛОЖЕНИИ КОЛЕНВАЛА ДОСТИГАЮТСЯ МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ СИЛ ИНЕРЦИИ ВОЗВРАТНО-ПОСТУПАТЕЛЬНО ДВИЖУЩИХСЯ МАСС. 3.7.1 основы теории двс 2012 моменты , действующие в кривошипно-шатунном механизме 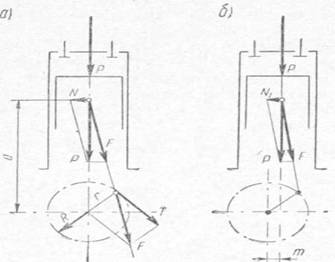 СИЛЫ ДАВЛЕНИЯ ГАЗОВ Р= Pz x F = Рz x пD2 /4 ( 2 ) где F- площадь поршня . По законам механики ее можно сосредоточить в центре поршневого пальца. При повороте коленчатого вала на некоторый угол сила Р разлагается на две составляющие: силу F, действующую по шатуну, и силу N, направленную перпендикулярно стенке цилиндра (нормальная сила). Перенеся силу F по линии ее действия к центру шатунной шейки и затем разложив ее на две составляющие, получим касательную силу Т, действующую по окружности вращения шатунной шейки, и радиальную силу R, направленную по кривошипу к центру вала. Действуя на плечо г (радиус кривошипа), сила Т создает вращение коленчатого вала, равный Вращающему моменту Мвр. = Т х r, где r- радиус кривошипа (3 ) Нормальная сила N прижимает поршень к стенке цилиндра, увеличивая трение поршня и износ цилиндра двигателя; кроме того, сила N, действуя на плечо а, создает опрокидывающий момент, равный Мопр.= N х а (4) где а- расстояние от оси поршневого пальца до оси коленвала стремящийся опрокинуть двигатель в сторону, обратную вращению коленчатого вала. Сила R, действующая по кривошипу, создает давление на коренные подшипники вала. Опрокидывающий момент влияет на износ боковых поверхностей поршня и стенок втулки цилиндра,изнашивая их бочкообразно. В некоторых двигателях для уменьшения действия нормальной силы N ось коленчатого вала смещают на величину m (у двигателей ГАЗ — до 3 мм); такой кривошипно-шатунный механизм называется дезаксиальным. При этом давления на стенку цилиндров несколько выравниваются: на левую стенку давление уменьшается, а на правую, менее нагруженную, увеличивается. Указанные силы при работе периодически меняются по величине и направлению и наибольшего значения достигают при рабочем ходе. 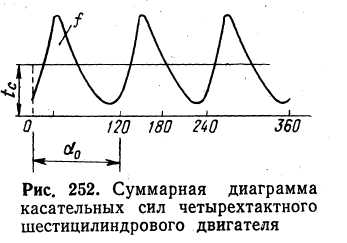 НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ Как видна из суммарной диаграммы касательных сил (см. рис. 252), касательная сила, а следовательно; и крутящий момент не остаются постоянными, вследствие чего коленчатый вал вращается неравномерно. Для; оценки неравномерности его вращения вводится понятие о степени неравномерности. Отношение разности максимальной и минимальной скоростей вращения за цикл работы к средней скорости называется степенью неравномерности и обозначается через δ. Согласно требованию Регистра для судовых двигателей, работающих непосредственно на винт, δ = 1/20-1/40 Работающих на электрогенератор δ = 1/100-1/300 Согласно определению, δ =(Vмакс-Vмин)/ Vср В связи со столь различными требованиями к к неравномерности вращения необходимо знать,от каких факторов она зависит. Известно ,что момент инерции равен произведению массы на квадрат расстояния центра тяжести тела от оси вращения. Тогда сумма моментов инерции ( кг х м2) вращающихся масс двигателя будет : I= Im +IP.o.+I w , где Im- момент инерции маховика, IP.o- момент инерции вращающихся частей ДВС, I w , -момент инерции движущихся частей КШМ. Значит обеспечить заданную степень неравномерности можно только подбором маховика. Для расчета используют величину пропорциональную моменту инерции- маховый момент: I = m D2 / 4g , где g- ускорение свободного падения. Нужное его значение может быть обеспечено как величиной массы, так и диаметра маховика. Однако диаметр маховика ограничивают по максимальному значению окружной скорости ( 70 м/с –для чугунных и 100 м/с – для стальных) для избежания его разрушения от центробежных сил. ОТВЕТИТЬ НА ВОПРОСЫ: 1. ПОКАЗАТЬ НА РИСУНКЕ,КАК ПОЛУЧАЮТСЯ ВРАЩАЮЩИЙ И ОПРОКИДЫВАЮЩИЙ МОМЕНТЫ. 2. ПРИ КАКОМ ПОЛОЖЕНИИ КРИВОШИПА БУДЕТ МАКСИМАЛЬНОЕ ЗНАЧЕНИЕ ВРАЩАЮЩЕГО МОМЕНТА. 3. ПОНЯТИЕ О СТЕПЕНИ НЕРАВНОМЕРНОСТИ ВРАЩЕНИЯ. 4. КАКИЕ ТРЕБОВАНИЯ ПРЕДЪЯВЛЯЕТ Российский Регистр к степени неравномерности судовых дизелей. 5. от каких факторов зависит степень неравномерности вращения. Тема 3.7.2 2012 ПОНЯТИЯ ОБ УРАВНОВЕШЕННОСТИ ДВИГАТЕЛЯ 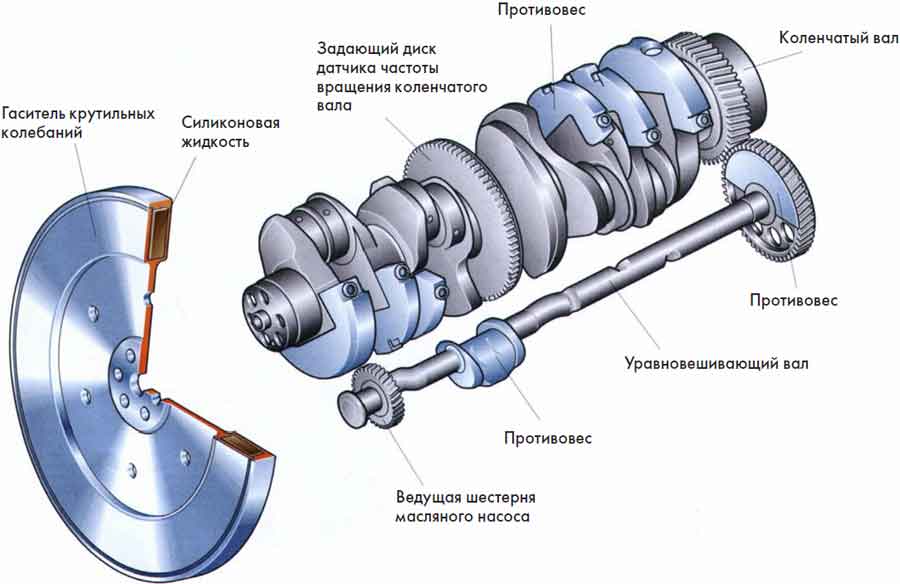 Один из недостатков ДВС –их способность вызывать вибрацию корпуса судна. Причиной являются силы инерции поступательно-движущихся частей ДВС В 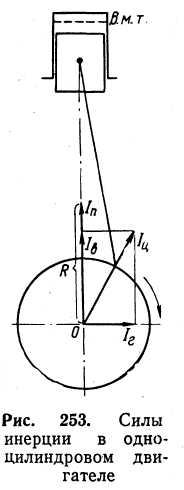 иды сил инерции. Поршневые двигатели во время работы могут вызывать сотрясения различной частоты вследствие действия в них периодических неуравновешенных сил.К периодическим неуравновешенным силам относятся силы инерции поступательно движущихся частей. Они нечем неуравновешенны в ДВС . Формула силы инерции Ри =-мп а , где а = - Rω2(cоsа + R/Lcos 2а) – ускорение поршня. Выполним преобразования ,получим: Ри = - мпRω2cоsа - λмп Rω2cos 2а Т.е сила инерции поступательно движущихся частей являтся суммой двух сил: - мпRω2cоsа = Ри1 ----силы инерции первого порядка. Совпадают с частотой вращения коленвала и вызывают общую вибрацию корпуса λмп Rω2cos 2а = Ри2 -----силы инерции второго прядка. Частота колебаний вдвое больше частоты вращения коленвала . вызывает местные вибрации –переборок,листов и т.д. Неуравновешенными являются также центробежные силы вращающихся частей- кривошип и нижняя часть шатуна. Рц= Мв Rω2 на рисунке- Iц Значение этой силы постоянно, но изменяется ее направление и ее составляющие Ie. Ib будут вызывать вертикальные и горизонтальные вибрации. Обеспечение уравновешенности. При оценке уравновешенности принято лишь об неуравновешенных силах. Ввиду того что неуравновешенные силы инерции вызывают дополнительные напряжения и преждевременный износ отдельных частей двигателя, необходимо стремиться к тому, чтобы силы инерции и их моменты были уравновешены. Существует два условия равновесия работающего двигателя.:
Исследования сумм сил инерции и их моментов позволяют сделать следующий вывод-- полностью уравновешенными являются двигатели с четным числом цилиндров 6 и более при зеркальном расположении кривошипов. В этом случае при работе ДВС суммы всех сил инерции и моментов в любой момент времени равны нулю на установившихся режимах Если при проектировании ДВС это условие не выполняется (нечетное число цилиндров например) то применяют следующие меры.
ОТВЕТИТЬ НА ВОПРОСЫ: 1. КАКУЮ ВИБРАЦИЮ ВЫЗЫВАЮТ СИЛЫ ИНЕРЦИИ 1-ГО И 2-ГО ПОРЯДКА. 2. КАКОЙ ДВИГАТЕЛЬ СЧИТАЕТСЯ ПОЛНОСТЬЮ УРАВНОВЕШЕННЫМ. 3. ДЛЯ ЧЕГО УСТАНАВЛИВАЮТ ПРОТИВОВЕСЫ И ГДЕ. 4. ПОЧЕМУ ВЕС ПОРШНЕЙ И ШАТУНОВ ДОЛЖЕН БЫТЬ ОДИНАКОВ ( В ДОПУСТИМЫХ ПРЕДЕЛАХ ДЛЯ ДАННОЙ МАРКИ ДВС) |