платежная матрица в задачах выбора. STW КР Платежная матрица. Платежная матрица в задачах выбора и принятии решений
 Скачать 124.35 Kb. Скачать 124.35 Kb.
|
1 2 Платежная матрица в задачах выбора и принятии решений  Содержание Введение 3 1. Основные теоретические положения метода платежных матриц 4 2. Пример экономической постановки задачи с использованием платежной матрицы 16 Список литературы 23 Введение Выполнение управленческих функций неразрывно связано с эффективным принятием решений. На этом основании закономерно утверждать, что процесс принятия решений является центральным пунктом теории управления. Теория управления решает ряд задач, наиболее важной среди которых следует признать повышение эффективности функционирования организаций за счет рационального применения способностей, а также расширения знаний руководства в сфере принятия обоснованных управленческих решений в сложных ситуациях с помощью моделей и количественных методов. Большинство известных методов принятия решений, которые используется в процессе управления, можно условно отнести к отдельной разновидности моделирования. Вместе с тем, термин «модель» традиционно относится лишь к общим методам анализа, а также к многочисленным их специфическим разновидностям. Однако, методический инструментарий моделирования включает и ряд методов, пригодных для обоснования выбора среди нескольких имеющихся альтернатив наиболее эффективного решения, которое в наибольшей мере способствует достижению целей. В частности, к таким методам относится платежная матрица. Целью данного исследования является изучение теоретических и методических аспектов применения платежной матрицы в процессе обоснования управленческих решений. Основные теоретические положения метода платежных матриц Как отмечают специалисты в области моделирования, не смотря на простоту, некоторые модели, используемые в производственном менеджменте, настолько сложны, что без компьютера обойтись невозможно. В то же время, концепция моделирования проста. По определению Шеннона: «МОДЕЛЬ - это представление объекта, системы или идеи в некоторой форме, отличной от самой целостности». Одним из примеров модели является схема организации, представляющая ее структуру. Главной характерной особенностью модели принято считать упрощение реальной жизненной ситуации, для которой она используется. Учитывая, что структура и форма модели менее сложна, а не относящиеся к сути проблемы ее параметры, в нее не включаются, модель зачастую способствует более отчётливому пониманию и разрешению проблем, встающих перед субъектом, который принимает решения. Число всевозможных конкретных моделей науки управления чрезвычайно велико и в полной мере отвечает тому количеству проблем, для разрешения которых они были разработаны. В наиболее общем случае суть каждого принимаемого руководством решения сводится к выбору наилучшей из имеющихся альтернатив по конкретным предварительно заданным критериям. Одним из методов статистической теории решений, который является полезным при необходимости обоснования выбора одного из нескольких вариантов, является платежная матрица. Ее практическая значимость возрастает в ситуациях, когда необходимо определить стратегию, которая в наибольшей мере будет способствовать достижению целей. По словам Н. Пола Лумбы: «Платеж представляет собой денежное вознаграждение или полезность, являющиеся следствием конкретной стратегии в сочетании с конкретными обстоятельствами. Если платежи представить в форме таблицы (или матрицы), мы получаем платежную матрицу». При рассмотрении ключевых положений метода платежных матриц принципиально важное значение получают особенности условий применения стратегии, которые возникают в связи с наличием так называемых «конкретных обстоятельств», поскольку они определяют, в каких случаях следует использовать платежную матрицу, а также позволяют определить, когда принятое на ее основе решение будет надежным с наибольшей вероятностью. Вообще, матрица означает, что платеж зависит от определенных событий, которые фактически происходят. Если предусмотренной событие или состояние природы не возникает, платеж неизбежно будет иным. В практике принятия управленческих решений платежная матрица полезна, когда: 1) есть в наличии разумно ограниченное число альтернатив или вариантов стратегии и необходимо сделать обоснованный выбор между ними. 2) сценарии возможных событий с полной определенностью не определены. 3) результаты принятого решения определяются выбранными альтернативами, а также теми событиями, которые имеют место в действительности. Рассмотрим ключевые принципы применения метода платежной матрицы. Макет платежной матрицы представлен в таблице 1. Ее строки соответствует различным альтернативным вариантам событий -x1, x2, …, xM , а столбцы - наиболее вероятным значениям реализации стратегий - S1, S2, …, SN . Общий элемент платежной матрицы Зji - расчетное альтернативное значение стратегии для j-го альтернативного варианта событий и i-го сочетания исходных данных, от которых зависят сценарии развития событий. Таблица 1. Платежная матрица З = ||Зji||
Для руководителя также важно иметь возможность объективной оценки вероятности событий по каждому сценарию, а также владеть инструментарием определения ожидаемой вероятности. Очевидно, руководитель редко располагает таким объемом информации, которая обеспечивает ситуацию полной определенности, в то же время, следует признать, что он также очень редко оказывается в условиях полной неопределенности. В большинстве случаев принятия решений руководителю предстоит оценивать вероятность наступления событий или их возможность. Вероятность событий, как известно, варьирует в интервале от 0 до 1. При этом вероятность равна 1, когда событие определенно произойдет, и 0 - когда событие однозначно не произойдет. Вероятность можно определить объективно, опираясь на прошлые тенденции, или субъективно, исходя из ожиданий руководителя, который руководствуется собственным опытом в подобных ситуациях. В случаях, когда вероятность не была принята в расчет, решение всегда будет тяготеть в направлении наиболее оптимистических последствий. Вероятность является фактором прямого влияния на величину ожидаемого значения результативного показателя платежной матрицы. Исходя из этого, ожидаемое значение альтернативы или варианта стратегии определяется как сумма произведений возможных значений принятых к рассмотрению событий и вероятностей их наступления. На основании информации об ожидаемых значениях для каждого альтернативного варианта событий, а также результатах наступления событий (такая информация должна быть представлена в виде матрицы), руководитель получает возможность обосновать наиболее оптимальное решений при заданных критериях. Как правило, он будет соответствовать наивысшему ожидаемому значению. На первом этапе анализа, на основе платежной матрицы З = ||Зji|| рассчитывается матрица рисков - =||ji|| . Для определения значения риска ji для варианта развития событий xj и сочетания исходных данных применяется следующая формула: 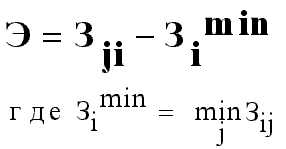 (1) (1)При принятии решений с помощью метода платежной матрицы руководствуются определенными правилами. Прежде всего, речь идет о специальных критериях принятия решения в условиях неопределенности и риска. Среди таких критериев наиболее востребованными являются: Критерий Лапласа (минимумы среднеарифметических затрат Зj ); Критерий Вальда (минимальных затрат или максимальной полезности); Критерий Сэвиджа (минимального риска); Критерий Гурвица. Максиминный критерий Вальда. Согласно критерию Вальда игра с природой рассматривается как игра с разумным, однако, агрессивным противником, который всеми возможными способами препятствует игроку и пытается помешать ему в достижении успеха. По данному критерию оптимальной считается стратегия, при которой игрок гарантированно получает выигрыш в размере, который не может быть меньше, чем "нижняя цена игры с природой": α= 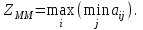 (2) (2)В соответствии с критерием Вальда (максиминным критерием) для обоснования выбора оптимального решения применяется следующее правило: в платёжную матрицу вводится дополнительный столбец из наименьших результатов аir каждой строки. Среди этих вариантов выбрать следует те, по которым в строках матрицы стоят наибольшие значения аir этого столбца. Это позволяет полностью исключить риск для выбранных вариантов, а значит, принимающий решение субъект не может столкнуться с худшим результатом, чем тот, на который он располагает. Независимо от условий, соответствующий результат не может оказаться ниже ZMM. Это свойство позволяет отнести максиминный критерий к категории фундаментальных. Поэтому он чаще всего применяется в технических задачах. Однако утверждение об отсутствии риска также характеризуется различными потерями. Рассмотрим последовательность применения критерия Вальда на примере (см. таблицу 2). Таблица 2. Матрица вариантов решения без учёта риска
Среди предложенных вариантов по критерию Вальда оптимальным является вариант X2, выбирая который мы избегаем неудачного значения 1, реализующего в варианте X1 при внешнем состоянии B1, получая вместо него при этом состоянии немного лучший результат 1,1. Вместе с тем, при развитии событий по варианту Х1 игрок теряет выигрыш 10, который возможен в состоянии В2, получая лишь 1,1. Данный пример доказывает, что во многих практических ситуациях, придерживаясь пессимистической стратегии, исход событий на основании минимаксного критерия может оказаться невыгодным. Применение критерия Вальда оправдано в тех случаях, когда ситуация, для которой принимается решение, соответствует следующим условиям: о возможности появления внешних состояний Вj ничего не известно; приходится считаться с появлением различных внешних состояний Вj; решение выполняется только один раз; необходимо исключить какой бы то ни было риск, т.е. ни при каких условиях Вj не допускается возможность того, чтобы результат оказался меньше, чем ZMM. ZHW = 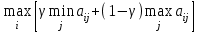 , (3) , (3)где — “степень пессимизма” ("коэффициент пессимизма", весовой множитель), 0 1. Для выбора оптимального решения на основании оценочного критерия Гурвица (HW – критерия) применяется следующее правило: в матрицу решений вводится дополнительный столбец, который содержит средние взвешенные значения наименьшего и наибольшего результатов каждой строки. Среди полученных комбинаций следует выбирать те варианты Xi, в строках которых стоят наибольшие элементы air этого столбца. При =1 критерий Гурвица (3) тождественен критерию Вальда, а при =0 – критерию крайнего оптимизма (критерию азартного игрока), который предполагает делать выбор в пользу стратегии с максимальным выигрышем в строке. Учитывая, что крайне сложно определить значения долей оптимизма и пессимизма, которые имеют место при принятии решения. Исходя из этого, в качестве некоторой "средней" точки зрения чаще всего принимается весовой множитель =0,5. Следует также отметить, что значение степени пессимизма во многом определяется мерой ответственности: чем более значимы последствия ошибочных решений, тем сильнее желание субъекта, принимающего решение, застраховаться. При этом степень его пессимизма ближе к единице. Рассмотрим последовательность применения критерия Гурвица для некоторой комбинации сценариев событий (данные представлены в таблице 2) и степени пессимизма =0,6. Как видно, для стратегии X1 минимальное значение равно 1, а максимальное – 10. Применяя формулу (3), рассчитаем а1r=0,6*1+0,4*10=4,6. Аналогичным способом определим искомый критерий для второй стратегии. Далее определим максимальное значение столбца аir. В результате получим платежную матрицу следующего вида (табл. 3). Таблица 3
Таким образом, по критерию Гурвица при =0,6 следует выбирать стратегию X1. Следует отметить, что в специальной литературе часто находит применение и такая модификация критерия Гурвица: ZHW = 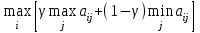 , (4) , (4)где - “степень оптимизма” ("коэффициент оптимизма ", весовой множитель), 01. При =0 критерий Гурвица (4) тождественен критерию Вальда, а при =1 совпадает с максиминным решением. Согласно критерию Гурвица ситуация, в которой принимается решение, должна отвечать следующим условиям: о вероятностях появления Вj ничего не известно; с появлением состояний Вj необходимо считаться; реализуется лишь малое количество решений; допускается некоторый риск. Руководствуясь принципом Сэвиджа, каждому решению соответствует некоторая величина дополнительных потерь, связанных с реализацией такого решения. Тогда, правильное решение не влечет за собой никаких дополнительных потерь, и их величина равна нулю. В свою очередь, для выбранного решения всегда можно рассчитать определенное соотношение дополнительных потерь по сравнению с реализацией решения, правильного при данном состоянии природы. Важно помнить, что при выборе решения, наиболее адекватного различным состояниям природы, необходимо принимать во внимание только эти дополнительные потери, потому что они и показывают следствия ошибок выбора. Алгоритм решения задачи предполагает, что на первом этапе должна быть построена так называемая “матрица рисков”. Ее элементы показывают, какой убыток понесет принимающий решения субъект в результате выбора неоптимального варианта решения. В данном случае принципиальное значение приобретает категория риска. Так, в случае обоснования выбора стратегии i в условиях (состояниях) природы j понятие риска рассматривается как разность между максимальным выигрышем, который можно получить в этих условиях и выигрышем, который получит игрок в тех же условиях, применяя стратегию i. Следуя данной логике, игрок, которому заранее известно будущее состояние природы j, выберет стратегию, которой соответствует максимальный элемент в данном столбце: 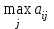 , и тогда риск: , и тогда риск: 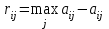 . .Руководствуясь критерием Сэвиджа, в условиях неопределенности следует выбирать решение, которое обеспечивает минимальное значение максимального риска: ZS= 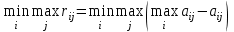 . (4) . (4)Рассмотрим применение критерия Сэвиджа для данных таблицы 3. Строим матрицу "рисков" для этого находим максимальные значения для каждого столбца таблицы 1. Они равны 1.1; 10 и 1.2 соответственно и находим значения рисков по формуле 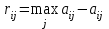 . Далее платежную матрицу необходимо дополнить столбцом наибольших разностей. На следующем этапе необходимо выбрать те варианты, для которых в строках находится наименьшее для этого столбца значение. По результатам произведённых аналитических процедур составим таблицу 4. . Далее платежную матрицу необходимо дополнить столбцом наибольших разностей. На следующем этапе необходимо выбрать те варианты, для которых в строках находится наименьшее для этого столбца значение. По результатам произведённых аналитических процедур составим таблицу 4.Таблица 4. Матрица рисков
Таим образом, по критерию Сэвиджа наиболее оптимальной является стратегия X1 . Критерий Лапласа. В основу критерия положено предположение о том, что в силу неизвестности будущих состояний природы их вероятность следует считать одинаковой. Данный подход называется критерием недостаточного основания Лапласа. Для определения оптимальной стратегии по критерию Лапласа, необходимо для каждого варината подсчитать математическое ожидание выигрыша (вероятности состояний природы полагаются равными qj = 1/n, j = 1:n), и выбирать то решение, при котором значение этого выигрыша является максимальным. ZL= 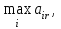 (5) (5)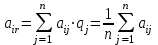 . (6) . (6)Учитывая, что гипотеза о равной вероятности различных состояний природы является довольно искусственной, считается, что принцип Лапласа может применяться в ограниченных случаях. В более общем случае следует считать, что состояния природы не равновероятны и использовать для обоснования выбора стратегии критерий Байеса-Лапласа. Критерий Байеса-Лапласа. Важным отличием критерия является то, что он отступает от условий полной неопределенности. Ученый предположил, что наступление возможных состояний природы характеризуется определенной вероятностью. Тогда, математическое ожидание выигрыша для каждого решения необходимо определять с учетом вероятности состояний природы. Среди полученных результатов следует выбирать тот, который дает наибольшее значение выигрыша: ZBL= 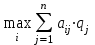 . (7) . (7)Метод Байеса-Лапласа предполагает возможность использования какой-либо предварительной информации о состояниях природы. При этом рассматриваются условия повторяемости состояний природы, а также повторяемости решений, и, прежде всего, наличие достаточно достоверных данных о прошлых состояниях природы. То есть, критерий предполагает возможность прогнозировать будущее состояние природы (статистический принцип), основываясь на предыдущих наблюдениях. Рассмотрим последовательность обоснования выбора стратегии по данным исходной таблицы 1. При этом предположим, что q1=0,4, q2=0,2 и q3=0,4. Последовательность шагов выполнения расчетов по критерию Байеса-Лапласа предусматривает, что на первом этапе таблицу 1 следует дополнить столбцом математических ожиданий. Далее, среди значений матрицы необходимо выбрать максимальное значение, как показано в таблице 5. Таблица 5.
1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||