платежная матрица в задачах выбора. STW КР Платежная матрица. Платежная матрица в задачах выбора и принятии решений
 Скачать 124.35 Kb. Скачать 124.35 Kb.
|
1 2 Таким образом, по критерию Байеса-Лапласа оптимальным является стратегия X1. Ситуации, для которых принимается решение по критерию Байеса-Лапласа, должна соответствовать следующим условиям: вероятности появления состояний Вj известны и не зависят от времени; решение реализуется (теоретически) бесконечное количество раз; для малого числа реализаций решения допускается некоторый риск. При достаточно большом количестве реализаций среднее значение постепенно стабилизируется. Поэтому при полной (бесконечной) реализации какой-либо риск исключён. Исходная позиция применяющего – критерий оптимистичнее, чем в случае с применением критерия Вальда, однако она предполагает более высокий уровень информированности и достаточно длинные реализации. Рассмотренные критерии не исчерпывают всего многообразия критериев выбора решения в условиях неопределенности, в частности, критериев выбора наилучших смешанных стратегий, однако и этого достаточно, чтобы проблема выбора решения стала неоднозначной. Результаты проведенных расчетов систематизированы в таблице 6. Из таблицы 6 видно, что выбор оптимального решения в значительной степени зависит от исходных допущений и выбранного критерия обоснования решения. Таблица 6. Оптимальные варианты, полученные с помощью различных критериев
Таким образом, выбор критерия, так же как и выбор принципа оптимальности, вполне обоснованно относится к категории наиболее сложных и ответственных задач в теории принятия решений. Вместе с тем, специалисты в области принятия решений обращают внимание на то, что конкретная ситуация, как правило, не бывает настолько неопределенной, чтобы нельзя было получить хотя бы частичной информации относительно вероятностного распределения состояний природы. В этом случае, оценив распределение вероятностей состояний природы, следует руководствоваться методом Байеса-Лапласа, либо необходимо провести эксперимент, который позволит уточнить сценарии поведения природы. Как показали результаты теоретического анализа, различные критерии принятия управленческих решений связаны с различными условиями, в которых принимаются такие решения. Именно поэтому, в теории принятия решений чаще всего применяются различные критерии, а затем проводится сравнительная оценка полученных результатов. Не менее важно для получения наиболее обоснованных результатов задействовать дополнительную информацию об изучаемой ситуации. Так, если принимаемое решение относится к сотням объектов с одинаковыми параметрами, то рекомендуется применять критерий Байеса-Лапласа. Если же количество таких объектов невелико, более обоснованно применять критерии минимакса или Сэвиджа. Таким образом, закономерным следует признать то обстоятельство, что различные критерии отдают предпочтение разным стратегиям, а значит, приводят к обоснованию различных выводов в отношении наиболее рационального решения. Вместе с тем, возможность выбора критерия позволяет ответственным исполнителям, принимающим управленческие решения, делать выбор, в зависимости от тех условий, которым соответствует та или иная ситуация. Любой критерий должен согласовываться с намерениями решающего задачу и соответствовать его характеру, знаниям и убеждениям. Следует отметить, что существуют и другие обобщенные критерии принятия решений, которые являются комбинациями выше перечисленных критериев. Однако все они, также не лишены ограничений и условностей и не могут обеспечить однозначного выбора варианта деятельности. Именно поэтому окончательный выбор варианта решения остается в компетенции экспертов и специалистов. 2. Пример экономической постановки задачи с использованием платежной матрицы Фермерскому хозяйству необходимо обосновать выбор наиболее эффективного способа выращивания свеклы на будущий сезон. Рассматриваются четыре возможных способа производства свеклы: Надежный (Н), Обычный (О), Рискованный (Р) и Инновационный (И). Стоимость затрат на производство свеклы каждым из указанных способов задана в таблице 7. Таблица 7. Стоимость затрат на производство свеклы различными способами (млн. руб.)
Урожайность свеклы (тонн) зависит от погодных условий и варианта сельскохозяйственной деятельности так, как задано в таблице 8. Таблица 8. Урожайность свеклы в зависимости от погодных условий при различных способах сельскохозяйственной деятельности (тонн)
Цены на свеклу на рынке зависят от средней урожайности в регионе (см. табл. 9). Таблица 9. Рыночная цена свеклы в регионе в зависимости от погодных условий (тыс. руб. за тонну)
Вероятность той или иной погоды в регионе проживания фермера задается таблицей 10. Таблица 10. Вероятность вариантов погоды в регионе проживания фермера (%)
Кроме того, фермер знает, что по ряду причин на рынке удается продать обычно не более Q тонн свеклы. Оставшуюся свеклу можно сдать перекупщикам по цене C тыс. руб. за тонну. Q = 2000 – 50 х 4 – 100 х 2 = 1600 тонн ; С = 4 – 0,1 (2+4) = 3,4 тыс. руб. ; k = 0,05 (2+4+1) = 0,35. Задание 1. Записать условие задания со своими исходными данными. 2. Определить оптимальную деятельность фермера по каждому из критериев (Байеса, Вальда, Гурвица, Сэвиджа). (Для критерия Гурвица принять коэффициент пессимизма равным k ). 3. Описать для данной конкретной задачи те ситуации (экономические и психологические особенности), при которых фермеру логичнее будет опираться на тот или иной критерий или несколько критериев. 4. Записать четкое управленческое решение, опираясь на один или несколько критериев по своему выбору. Обосновать это решение. Решение Рассмотрим алгоритм расчета критериев оценки оптимальной стратегии. По критерию Байеса для каждой стратегии (строки) определяется средний ожидаемый результат как сумма произведений вдоль строки результатов на их вероятности: 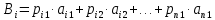 Лучшей является стратегия, для которой значение критерия Байеса наибольшее. Построим матрицу игры с природой для определения прибыли фермера по каждому сценарию событий (табл. 11). Таблица 11. Таблица для построения матрицы игры с природой
Рассчитаем прибыль фермера по каждому сценарию событий. При этом следует также принять во внимание дополнительные ограничения спроса на свеклу Q=1600 тонн и цены на оставшуюся свеклу С=3,4 тыс. руб. за тонну. Эти параметры будут применяться при определении дохода фермера в случае благоприятной погоды (табл. 12). Таблица 12. Матрица игры с природой
Рассчитаем среднюю ожидаемую прибыль фермера (табл. 13). Таблица 13. Таблица определения средней ожидаемой прибыли фермера
В1 = 12100х0,25+14710х0,40+21820х0,35 = 16456 тыс. руб. ; В2 = 16000х0,25+16810х0,40+16720х0,35 = 16576 тыс. руб. ; В3 = 28140х0,25+18310х0,40-5180х0,35 = 12546 тыс. руб. ; В4 = 7140х0,25+19262х0,40+14920х0,35 = 14711,8 тыс. руб. . ВI = max (16456; 16576; 12546; 14711,8) = 16576 = B2  C2 C2  The best (Bayes) The best (Bayes)Таким образом по критерию Байеса наилучший результат возможен по сценарию С2. По критерию Вальда для каждой стратегии (строки) определяется наименьший достижимый результат как минимальный элемент в строке: 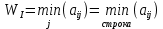 Лучшей при этом считается стратегия (сценарий), для которой этот результат наибольший: 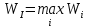 Рассчитаем критерий Вальда для условия задачи: 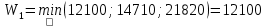 тыс. руб. ; тыс. руб. ;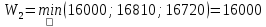 тыс. руб. ; тыс. руб. ;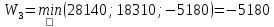 тыс. руб. ; тыс. руб. ;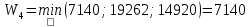 тыс. руб. тыс. руб. WI = max (12100; 16000; -5180; 7140) = 16000 = W2  C2 C2  The best (Wald) The best (Wald)Таким образом, по критерию Вальда наилучшей является стратегия (сценарий) С2, то есть при благоприятной погоде при стандартном способе производства свеклы. В критерии Гурвица для каждой стратегии определяется «взвешенный» результат из самого пессимистического и самого оптимистического для данной стратегии (сценария). Вес каждого определяется так называемыми коэффициентами пессимизма и оптимизма, сумма которых равна единице. После задания коэффициента пессимизма k и коэффициента оптимизма (1-k) для каждой стратегии (сценария) необходимо определить пессимистический Вi оптимистический Оi варианты и вычисляют критерий Гурвица : Hi = k·Bi + (1-k)·Oi Лучшей по критерию Гурвица считается стратегия (сценарий), для которой этот результат наибольший: 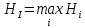 Рассчитаем критерий Гурвица для случая в нашей задаче. По условию, коэффициент пессимизма установлен на уровне 0,35. Тогда коэффициент оптимизма составляет 1-0,35 = 0,65. 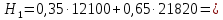 18418 тыс. руб. ; 18418 тыс. руб. ;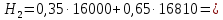 16526,5 тыс. руб. ; 16526,5 тыс. руб. ;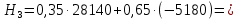 6482 тыс. руб. ; 6482 тыс. руб. ;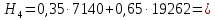 15019,3 тыс. руб. 15019,3 тыс. руб. HI = max (18418; 16526,5; 6482; 15019,3) = 18418 = H1  C1 C1  The best (Hurwich) The best (Hurwich)Таким образом, по критерию Гурвица наилучшей является стратегия (сценарий) С1, т.е. по этому критерию наиболее благоприятным для фермера представляется сценарий производства свеклы надежным способом. По критерию Сэвиджа сначала строится матрица (таблица) рисков, руководствуясь следующим алгоритмом: - матрица строится по столбцам; - в каждом столбце находим самое большое значение выигрыша; - из этого значения по очереди вычитают все значения в данном столбце и записывают результат в те же позиции. Символьно данная процедура имеет вид: 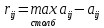 Построим матрицу рисков для условия нашей задачи. Максимальный элемент в первом столбце исходной матрицы равен 28140. Вычитая из этого значения остальные элементы столбца, получаем: 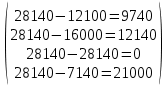 , т.е. первый столбец матрицы рисков равен , т.е. первый столбец матрицы рисков равен 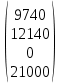 . .Аналогично находим элементы других столбцов: 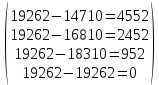 = =  ; ;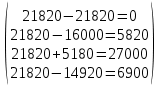 = = 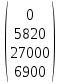 . .Таким образом, матрица рисков имеет вид:  = = 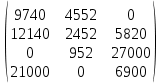 . .Элементы матрицы рисков показывают «недополучение» оптимальной прибыли из-за неверного выбора стратегии при данном состоянии природы. Далее в каждой строке матрицы рисков определяется наибольший результат (максимальный элемент в строке): 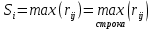 . . Лучшей по критерию Сэвиджа является стратегия, для которой этот результат наименьший: 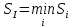 Определим критерий Сэвиджа для условий задачи. 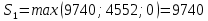 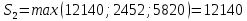 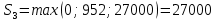 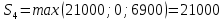 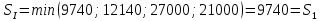  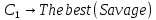 Таким образом, по критерию Сэвиджа наилучшей является стратегия С1, которая предусматривает производство свеклы надежным способом, в данном случае мы рискуем потерять наименьшую прибыль среди возможных вариантов получения. Для формирования окончательных выводов систематизируем результаты расчетов по разным критериям. C2 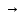 The best (Bayes) The best (Bayes)C2  The best (Wald) The best (Wald)C1  The best (Hurwich) The best (Hurwich)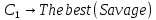 Как видно, фермер может воспользоваться стратегиями С1 и С2, которые обеспечивают ему возможность получения наилучших результатов деятельности. Таким образом, по совокупности критериев фермеру целесообразно применить стратегии С1 или С2 – использовать для производства свеклы надежный или стандартный способ производства. Список литературы Грешилов А. А. Математические методы принятия решений — М.: Издательство МГТУ им. Н. Э. Баумана, 2006 .— 583, [1] с.: ил. Дорогов, В. Г. Введение в методы и алгоритмы принятия решений: Учебное пособие / В.Г.Дорогов, Я.О.Теплова. – М.: ИД ФОРУМ: ИНФРА-М, 2012. - 240 с. – режим доступа http://znanium.com. Исследование операций в экономике : учеб. пособие / под ред. Н.Ш. Кремера – 2-е изд., перераб. и доп. – М. : Юрайт, 2010. – 430с. Петровский А. Б. Теория принятия решений — М.: Издательский центр «Академия», 2009 .— 398, [1] с.: ил. Соколов, А. В. Методы оптимальных решений. В 2 т. Т. 1. Общие положения. Математическое программирование: Учебное пособие / Соколов А.В., Токарев В.В. − М.: ФИЗМАТЛИТ, 2011. – 564 с. Токарев, В.В. Методы оптимальных решений. В 2 т. Т.2. Многокритериальность. Динамика. Неопределенность.: Учебное пособие / Токарев В.В. – М.: ФИЗМАТЛИТ, 2011. – 420 с. Фатхутдинов, Р. А. Управленческие решения: Учебник / Р.А. Фатхутдинов. − М.: ИНФРА-М, 2010. − 344 с. – режим доступа http://znanium.com. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении. — М.: Дело, 2000. — 431 с. Эддоус М., Стэнсфилд Р. Методы принятия решений. — М.: Аудит, ЮНИТИ, 1997. — 590 с. 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
