Контрольная работа №1 (2). Площадь трапеции
 Скачать 51.23 Kb. Скачать 51.23 Kb.
|
|
Контрольная работа №1 Вариант № 1 1. Решите старинную задачу разными способами (арифметическим, алгебраическим): Для перевозки 25 зеркал нанят извозчик с условием заплатить ему по 1р.50 к. за доставку каждого зеркала в целости и вычесть с него по 5 рублей за каждое разбитое им зеркало. На дороге извозчик действительно разбил несколько зеркал и за перевозку получил только 18 рублей. Сколько зеркал он доставил в целости? 2. Во время педпрактики студент проводил урок геометрии в 8 классе по теме «Площадь трапеции». Работу с теоремой он начал с вопроса: «Не знаете ли вы формулу площади трапеции?». Не получив ответа, он сделал на доске рисунок, ввел обозначения и записал формулу. Далее он спросил: «Не знаете ли вы доказательство этой теоремы?». Никто не ответил и тогда он сам начал доказывать её. а) Проанализируйте данную педагогическую ситуацию. б) Сформулируйте теорему, сделайте чертеж, введите обозначения, запишите кратко условие теоремы; в) докажите теорему со ссылками на используемые факты, известные определения, теоремы. г) Рассмотрите всевозможные случаи разбиения трапеции. Предложите вариант методики организации групповой формы деятельности учащихся при доказательстве теоремы. д) Какие знания и умения понадобятся учащимся для решения поставленной задачи? Ответы на вопросы представьте в виде наглядных схем. 3. Даны две функции у= 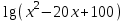 и у = и у =  . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти).К какому уровню дифференциации Вы отнесете каждую из них? 4. При решении уравнения 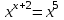 ученик привел такое решение ученик привел такое решение 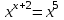 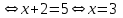 . В чем причина ошибок? Какова методика работы учителя с такими ошибками? Приведите правильное решение. . В чем причина ошибок? Какова методика работы учителя с такими ошибками? Приведите правильное решение. Вариант № 2 1.. Решите задачу из «Арифметики» Л.Ф. Магницкого разными способами (арифметическим, алгебраическим): "Некий человек нанял работника на год, обещал ему дать 12 руб. и кафтан. Но тот, отработав 7 месяцев, захотел уйти и просил достойной платы с кафтаном. Хозяин дал ему по достоинству расчет 5 р. и кафтан. Спрашивается, а какой цены тот кафтан был?" 2. Представьте, что в период педпрактики в школе Вы присутствуете на уроке геометрии в 8 классе. Как только учитель записал на доске новую тему «Свойства и признаки равнобедренной трапеции», его вдруг неожиданно вызвали с урока. Чтобы не прерывать урок, он попросила Вас продолжить урок. Чтобы выиграть хоть несколько минут и вспомнить свойства и признаки, Вы предложили детям по группам исследовать свойства равнобедренной трапеции. а) Какие задания Вы дадите группам? б) Сформулируйте свойства, сделайте чертеж, введите обозначения, запишите кратко условия теорем; в) докажите теоремы со ссылками на используемые факты, известные определения, теоремы. г) Сформулируйте признаки равнобедренной трапеции и докажите их. д) Может ли равнобедренная трапеция быть прямоугольной? А, наоборот? Почему? Ответы на вопросы представьте в виде наглядных схем. 3. Даны две функции у= 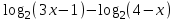 и у = и у =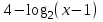 . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них? . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них?4. На выпускных экзаменах была предложена задача: найти область определения выражения ( х- 8)1/3 + lg  . Вася, претендующий на медаль, написал ответ: х Î . Вася, претендующий на медаль, написал ответ: х Î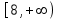 . Петя, претендующий на медаль, написал ответ: х Î ( -µ-1) È (2, + µ). Кто из них прав ? Какова методика работы учителя с такими ошибками? Приведите правильное решение. . Петя, претендующий на медаль, написал ответ: х Î ( -µ-1) È (2, + µ). Кто из них прав ? Какова методика работы учителя с такими ошибками? Приведите правильное решение. Вариант № 3 1. Решите старинную задачу разными способами (арифметическим, алгебраическим): Некто согласился работать с условием получить в конце года одежду и 10 флоринов. Но по истечении 7 месяцев прекратил работу и при расчете получил одежду и 2 флорина. Во сколько оценивалась одежда? 2. В курсе геометрии 7 класса учащиеся изучают теорему о сумме углов треугольника. А) Сформулируйте ее. Б) Какие свойства прямоугольных треугольников можно получить с помощью этой теоремы? Сформулируйте свойства в виде теорем. В) Докажите их. Г) Какая форма учебной деятельности учащихся будет эффективной при изучении этих свойств прямоугольного треугольника? Д)Какие знания и умения необходимы для их доказательства? Ответы на вопросы представьте в виде наглядных схем. 3. Даны две функции у=  и у =1 - и у =1 - 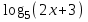 . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них? . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них?4. При решении уравнения  , ученик не находя ОДЗ, пришел к системе: , ученик не находя ОДЗ, пришел к системе: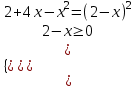 , утверждая, что этот переход обеспечивает равносильность. Прав ли ученик? Каков же правильный ответ? Какова методика работы учителя с такими ошибками? Приведите правильное решение. , утверждая, что этот переход обеспечивает равносильность. Прав ли ученик? Каков же правильный ответ? Какова методика работы учителя с такими ошибками? Приведите правильное решение. Вариант № 4 1. Решите старинную задачу разными способами (арифметическим, алгебраическим): Один путник идет от города в дом, а ходу его будет 17 дней, а другой путешественник от дома до города тот же путь может пройти в 20 дней. Оба эти человека пошли в один и тот же час от своих мест, и спрашивается, в сколько дней сойдутся? 2. Каждому студенту знакома теорема о средней линии треугольника, которую учащиеся изучают в курсе геометрии 8 класса. А) Сформулируйте теорему о средней линии треугольника. Б) Докажите её на основе признаков подобия треугольников; В) векторным методом. Г) Какой из способов доказательства Вы предпочтете, если эта тема попадется Вам в период педпрактики? Д) Какие знания и умения необходимы для доказательства каждым способом? Ответы на вопросы представьте в виде наглядных схем. 3. Даны две функции у= 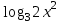 и у =. и у =. . . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них? 4. Прав ли ученик, представивший такое решение:  Ответ: ( - ; - 2) 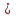 (2;).Какова методика работы учителя с такими ошибками? Приведите правильное решение. (2;).Какова методика работы учителя с такими ошибками? Приведите правильное решение. Вариант № 5 1. Решите старинную задачу разными способами (арифметическим, алгебраическим): "Подрядчик нанял работника с условием за каждый день платить ему по 75 коп., а за каждый праздный день удерживать с него по 15 коп. По происшествии 30 дней работнику следовало выдать 18 руб. Сколько дней он работал? 2 Каждому студенту знакома теорема Пифагора, которую учащиеся изучают в курсе геометрии 8 класса. А) Вспомните формулировку теоремы Пифагора. Б) Какое ей можно дать истолкование, используя понятие площади? В) Как, используя теорему Пифагора можно получить с учащимися на уроке различные следствия, например: выражение длины высоты любого треугольника через длины его сторон; Г) формулу Герона? Д) Какие знания и умения необходимы для доказательства каждого следствия? Ответы на вопросы представьте в виде наглядных схем. 3. Даны две функции у= 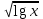 и у = и у = . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них? . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них? 4. Ученик, решая уравнение  , нашел корень х = -8, который отбросил, как посторонний. В ответе он записал, что уравнение не имеет корней. Какая ошибка могла быть допущена учеником? Каковы причины допущенной ошибки? Какова методика работы учителя с такими ошибками? Приведите правильное решение. , нашел корень х = -8, который отбросил, как посторонний. В ответе он записал, что уравнение не имеет корней. Какая ошибка могла быть допущена учеником? Каковы причины допущенной ошибки? Какова методика работы учителя с такими ошибками? Приведите правильное решение. Вариант №6 1. Решите старинную задачу разными способами (арифметическим, алгебраическим): "Трем работникам поручено некоторое дело. Первый и второй кончили бы вместе данную работу в 12 дней, второй и третий в 20 дней, а первый и третий в 15 дней. Во сколько дней каждый может кончить работу без помощи других? 2. В курсе геометрии 8 класса учащиеся изучают тему «Параллелограммы и его свойства«. Ромб и квадрат - частные случаи параллелограммов, у них много общих свойств. а) Дайте определение ромба и квадрата через параллелограмм. Б)Какие общие свойства имеют ромб и квадрат? в) Докажите их. г) А в чем отличие ромба от квадрата? д)Сформулируйте их отличительные свойства и докажите их. Ответы на вопросы представьте в виде наглядных схем. 34. Даны две функции у=  и у = и у = . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них? . Сформулируйте различные вопросы к этому условию. Решите составленные вами задачи (не менее пяти). К какому уровню дифференциации Вы отнесете каждую из них? 4. На выпускных экзаменах была предложена задача: найти область определения выражения (2х- 7)1/3 + lg  . Миша, претендующий на медаль, написал ответ: х Î[3,5; +]. Коля, претендующий на медаль, написал ответ: х Î( -µ-2) È (1, + µ). Кто из них прав ? Какова методика работы учителя с такими ошибками? Приведите правильное решение. . Миша, претендующий на медаль, написал ответ: х Î[3,5; +]. Коля, претендующий на медаль, написал ответ: х Î( -µ-2) È (1, + µ). Кто из них прав ? Какова методика работы учителя с такими ошибками? Приведите правильное решение.Указание: Решить один вариант предложенной контрольной работы. |
