Статистика. По исходным данным к задаче 1 произведите группировку предприятий по фактическому выпуску продукции, образовав следующие группы в млн руб
 Скачать 142 Kb. Скачать 142 Kb.
|
Практическое задание
дисциплине
Пермь 20___ Задача 2 По исходным данным к задаче № 1 произведите группировку предприятий по фактическому выпуску продукции, образовав следующие группы (в млн. руб.): до 600, от 601 до 1200, от 1201 до 2000, от 2001 до 2800, от 2801 до 3800, свыше 3800. Для каждой группы подсчитайте: число предприятий, стоимость основных средств, выпуск продукции по плану, фактически в среднем на одно предприятие и процент выполнения плана, а также фактическую стоимость выпущенной продукции на один рубль основных средств. Вычислите удельный вес отдельных групп по числу предприятий. Результаты группировки изложите в табличной форме и сделайте краткие выводы, назовите вычисленные в таблице относительные величины. Исходные данные:
Решение: Сначала разнесём показатели по указанным группам и подсчитаем итоги. Для этого используем разработочную таблицу (таблица 1.1): Таблица 1.1 Разработочная таблица группировки предприятий по фактическому выпуску продукции.
Результаты группировки занесём в сводную таблицу и определим общие итоги по совокупности единиц наблюдения по каждому показателю (таблица 1.2). Таблица 1.2 Группировка предприятий по фактическому выпуску продукции
Более конкретный анализ взаимосвязи показателей можно сделать на основе аналитической группировки. Построим аналитические группировки и вычислим показатели: фактического выполнения плана в среднем на одно предприятие (таблица 1.3), процент выполнения плана (таблица 1.4), фактическую стоимость выпущенной продукции на один рубль основных средств (таблица 1.5). Таблица 1.3 Анализ фактического выпуска продукции
Таблица 1.4 Анализ выполнения плана
Исходя из данных таблицы 1.4, можно сделать вывод, что план максимально перевыполнили предприятия с фактическим выпуском более 3800 млн. руб., на втором месте по показателю реализации плана группа предприятий с фактическим выпуском продукции 1201-2000 млн. руб. Таблица 1.5 Зависимость фактического выпуска продукции предприятий от стоимости основных средств
Из таблицы 1.5 видно, что существует прямая зависимость фактического выпуска продукции от стоимости основных средств: чем выше стоимость основных средств, тем больше фактический выпуск продукции. В таблице 1.6 показан удельный вес отдельных групп по числу предприятий. Таблица 1.6 Удельный вес отдельных групп по числу предприятий
Задача 9 Численность населения и студентов в отдельных странах в первой половине 80-х годов характеризовалась следующими данными:
Определите численность студентов, приходившихся на 10000 человек населения в различных странах. Какую относительную величину вы вычислили? Прокомментируйте полученные результаты. Решение: Вычислим относительный показатель интенсивности: ОПИ = 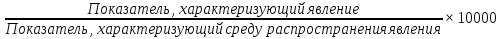 Вычисленные данные поместим в таблицу: Численность населения и студентов в отдельных странах в первой половине 80-х годов.
Таким образом, высокая численность студентов на 10000 чел. населения в США, СССР, Кубе. Низкая численность студентов на 10000 чел. населения наблюдалась в Китае, ГДР и Венгрии. Задача 16 Имеются следующие данные о выполнении месячного плана производства продукции металлургическими предприятиями:
Определите по пяти предприятиям средний процент выполнения плана. Решение: Для расчётов используем формулу нахождения средней арифметической: X = (106+102+105+98+110)/5 = 521/5 = 104,2% Вывод: средний процент выполнения месячного плана производства продукции равен 104,2%. Задача 23 Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
Требуется определить среднюю величину затрат рабочего времени и среднеквадратическое отклонение по способу моментов; коэффициент вариации; моду и медиану. Решение: Для расчета требуемых показателей составим таблицу:
Средняя величина затрат рабочего времени на 1 рабочего: 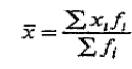 где 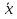 -среднее значение признака, серединное значение интервала, f-частота. -среднее значение признака, серединное значение интервала, f-частота.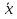 =3650/150=24,33 мин. =3650/150=24,33 мин.Следовательно, для данной совокупности типично, характерно тратить на однородную технологическую операцию 24,33 мин. Среднеквадратическое отклонение: 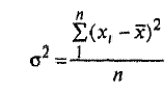 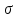 = =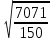 =6,87 мин. =6,87 мин.То есть длительность каждой однородной технологической операции отличается от средней величины на 6,87 мин. Коэффициент вариации: 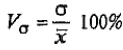 где σ - среднеквадратическое отклонение, 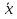 - средняя величина затрат. - средняя величина затрат.V=6,87/24,33*100%=28,23% Так как коэффициент вариации < 33%, данная совокупность является однородной. Определить моду:  М0[20-25]=20+5* 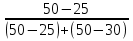 =22.78 мин., то есть наибольшая затрата рабочего времени на однородную технологическую операцию составляет 22,78 мин. =22.78 мин., то есть наибольшая затрата рабочего времени на однородную технологическую операцию составляет 22,78 мин.Определить медиану: Для нахождения медианы необходимо найти номер медианы (N): N= 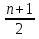 = =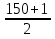 =75,5 чел. =75,5 чел.Из графы 7 таблицы видно, что 75,5 чел. приходится на интервал 20-25. Находи медиану на данном интервале по формуле: 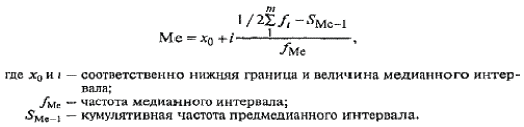 Me=20+5* 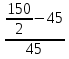 =23,33 мин., то есть половина (50%) рабочих тратит на однородную технологическую операцию менее 23,33 мин., а другая половина более 23,33 мин. =23,33 мин., то есть половина (50%) рабочих тратит на однородную технологическую операцию менее 23,33 мин., а другая половина более 23,33 мин.Задача 30 Имеются следующие данные о поступлении материалов на металлургическое предприятие:
Замените ряд ежемесячного поступления материала: 1) рядом квартального поступления; 2) рядом среднемесячного поступления материала по кварталам; 3) скользящими средними, приняв период сглаживания, равный трем месяцам. Нанесите на график фактические данные и средние показатели и произведите экономический анализ. Ответьте на вопрос: какова тенденция развития явления? Решение:
Расчет средних ведётся способом скольжения, то есть постепенным исключением из принятого периода скольжения первого уровня и включением следующего: 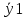 = = 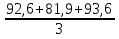 = = 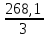 = 89,37 = 89,37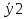 = =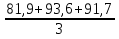 = = 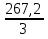 = 89,07 и т.д. = 89,07 и т.д.Полученные результаты заносим в таблицу:
Построим график: Рис. 1. Фактические данные и средние показатели Из рисунка 1 видно, что наблюдается общая тенденция роста, фактическое снижение объёмов поступления в некоторых месяцах сглаживается за счёт повышения поставок в другие месяцы. Задача 37 Имеются следующие данные по кирпичным заводам:
Определите:
а) переменного состава, б) постоянного состава;
Решение: Для расчета требуемых показателей составим таблицу:
1) Индекс динамики производительности труда найдём по формуле: 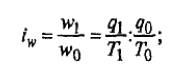 где w0, w1 - выработка за 1 день в базисном и отчётном периодах; q0, q1 - объём изготовленной продукции в базисном и отчётном периодах; Т0, Т1 - количество отработанных человеко-дней в базисном и отчётном периодах. iw1= 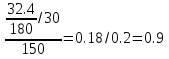 или 90% - снижение производительности труда на заводе №1 на 10% или 90% - снижение производительности труда на заводе №1 на 10%iw2= 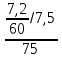 = 0,12/0,1=1,2 или 120% рост производительности труда на заводе №2 на 20%. = 0,12/0,1=1,2 или 120% рост производительности труда на заводе №2 на 20%.2) Индекс производительности труда: а) переменного состава: Iпс = 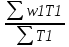 : :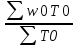 = = 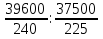 = 165:166,67 = 0,989 или 98,99% = 165:166,67 = 0,989 или 98,99%Снижение производительности труда на 1,01% б) постоянного состава: Iфс= 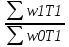 = =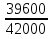 =0.943 или 94,28% =0.943 или 94,28%Если бы структура производительности труда не изменилась, то производительность снизилась на 5,72%. 3) Структурные сдвиги: Iстр= 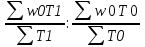 = =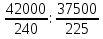 =1,0499 или 104,499% =1,0499 или 104,499%За счёт структурных сдвигов, а именно увеличения отработанных человеко-дней, при неизменной дневной выработке производительность увеличилась бы на 4,99%. 4) Абсолютный прирост: ΔwT(T)= 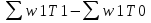 =39600-36000=3600 тыс. т =39600-36000=3600 тыс. тУвеличение средней производительности на 3600 тыс. т вследствие увеличения количества отработанных человеко-дней. ΔwТ(w)= 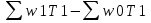 =39600-42000=-2400 тыс. т =39600-42000=-2400 тыс. тУменьшение средней производительности на 2400 тыс. т. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
