Математика. По классическому определению вероятности, вероятность события а равна
 Скачать 174.68 Kb. Скачать 174.68 Kb.
|
|
По классическому определению вероятности, вероятность события А равна 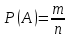 , где m – число благоприятных исходов, n – общее количество исходов , где m – число благоприятных исходов, n – общее количество исходовВ нашем случае, m=5, n=50 Тогда, вероятность вытащить окрашенную деталь: Р(А)=5/50=0,1 Площадь прямоугольника: Sпрям=a*b=3*4=12 (кв.ед) Т.к круг вписан в прямоугольник, то его радиус равен половине стороны а, т.е.3/2=1,5 Площадь круга: Sкруга=ПR2=3,14*1,5*1,5=7,065 (кв.ед) Тогда вероятность, что наугад брошенная точка попадет в круг: Р(А)=7,065/12=0,58875 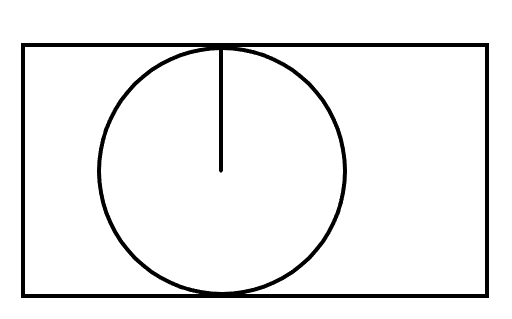 Т.к испытания независимые друг от друга, то чтобы найти общую вероятность, необходимо перемножить благоприятные исходы друг с другом. Тогда вероятность того, что все стрелки одновременно попадут в цель: Р(А)=0,8*0,7*0,65=0,364 4 из 6 МАЗ: 4/6 2 из 6 Вольво: 2/6 Сначала берут в аренду три авто, затем два. Благоприятный исход для трех автомобилей МАЗ 3 из 4: 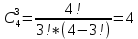 . Благоприятный исход для трех автомобилей Вольво 2 из 2 (их всего 2): . Благоприятный исход для трех автомобилей Вольво 2 из 2 (их всего 2): 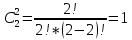 Всего берут в сумме 5 автомобилей из 6: 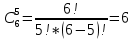 Т.к испытания независимые друг от друга, то чтобы найти общую вероятность, необходимо перемножить благоприятные исходы друг с другом. 4*1=4 По классическому определению вероятности, Р(А)=4/6=0,667 – вероятность того, что первая организация получит три МАЗА, а вторая – два Вольво По классическому определению вероятности, вероятность события А равна 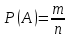 , где m – число благоприятных исходов, n – общее количество исходов , где m – число благоприятных исходов, n – общее количество исходовВ нашем случае, m=21+19=40 (количество изготовленных деталей второй и третьей бригадой, n=60 Р(А)=40/60=0,667 – вероятность поступления на сборку детали, изготовленной 2 или 3 бригадой Вероятность того, что первый шар будет белым равна количеству исходов вытащить белый шар из всей суммы шаров, находящихся в ящиках, т.е Всего белых шаров: 6+7+3=16, всего шаров в ящиках: 6+4+7+8+3+7=35 Тогда Р(А)=16/35=0,457. Вероятность того, что второй шар будет черным равна количеству исходов вытащить черный шар из всей оставшейся суммы шаров: Всего черных шаров: 4+8+7=19, всего шаров в ящиках: 6+4+7+8+3+7-1 (т.к. один шар уже вытащили) = 34 Тогда Р(В) = 19/34=0,559 Т.к испытания независимые друг от друга, то чтобы найти общую вероятность, необходимо перемножить благоприятные исходы друг с другом. Р(С)=0,457*0,559=0,225 – вероятность, что первым появится белый шар, а вторым - черный. Относительная частота (частость) – это отношение числа испытаний, в которых событие фактически появилось, к общему числу проведенных испытаний. Тогда для того, чтобы частость была равна 0,5016 при 12000 испытаниях, число удачных исходов должно быть равно: m=0,5016*12000=6019 Применим локальную теорему Лапласа. Если производится n независимых испытаний (n – велико), и вероятность наступления события А в каждом испытании постоянна и равна р, то вероятность того, что в n независимых испытаниях событие А наступит m раз, определяется по формуле: 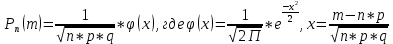 Вероятность выпадения герба равна вероятности выпадения решки и равна 0,5. Тогда, 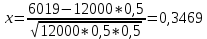 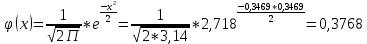 Таким образом Р(А) = 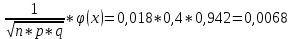 – вероятность появления частости 0,5016 при повторном опыте. – вероятность появления частости 0,5016 при повторном опыте.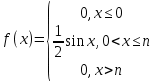 Найдем функцию распределения F(x) по определению 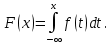 Получаем: Получаем:Пусть x≤0, тогда f(x) = 0, тогда 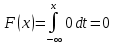 Пусть 0 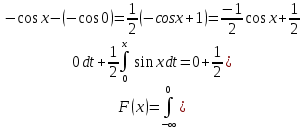 Пусть x>п, тогда f(x) = 0, тогда 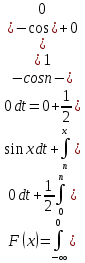 Таким образом, 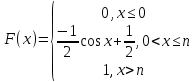 Построим график f(x): 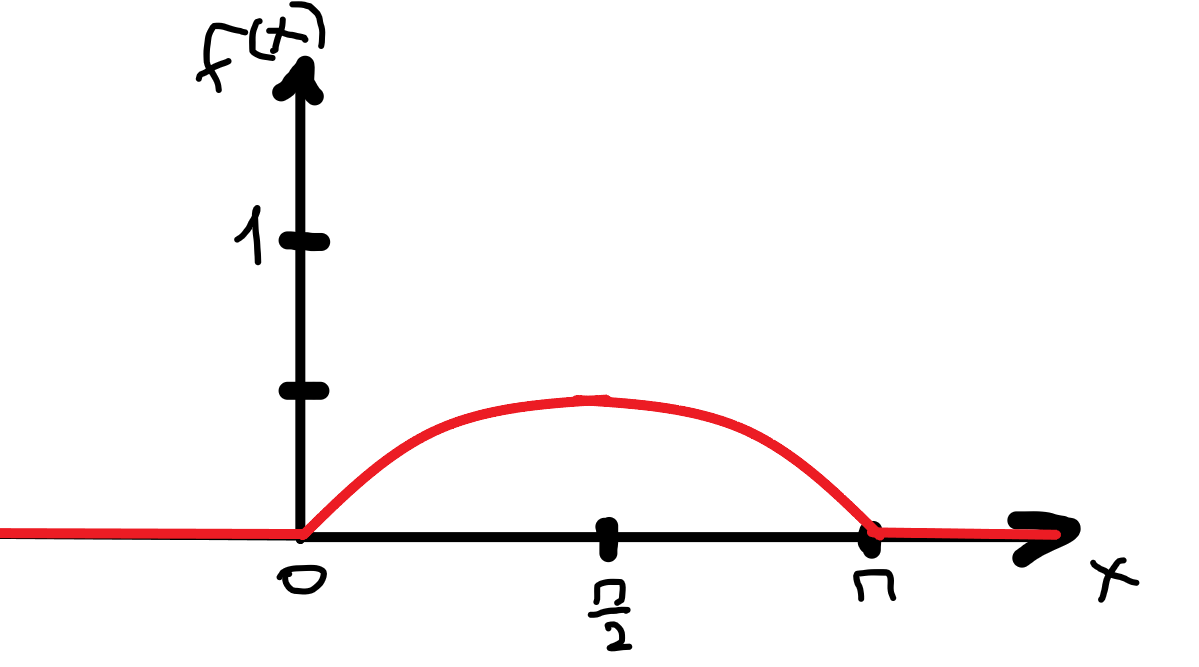 Построим график F(x): 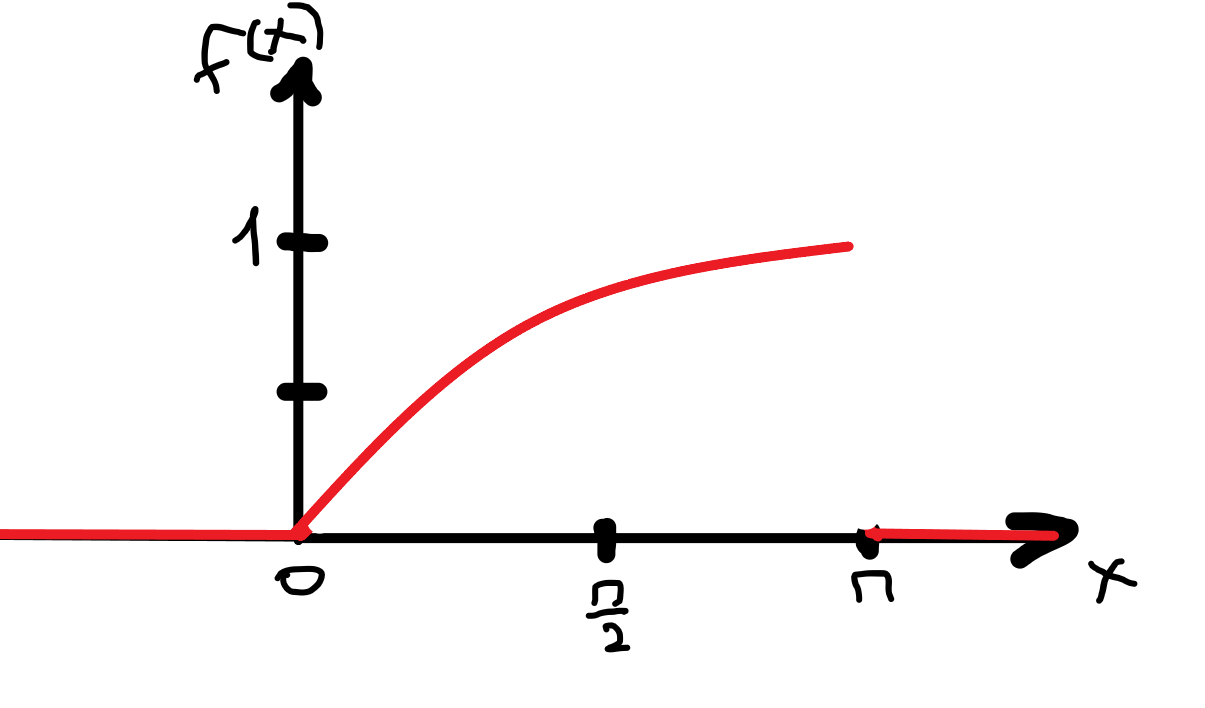 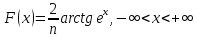 , (1,3) , (1,3) Вероятность попадания случайной величины в интервал (1,3) равна 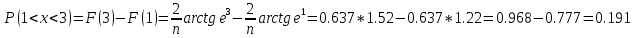 Найдем плотность распределения по формуле 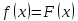 , откуда , откуда 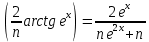 Построим график F(x): 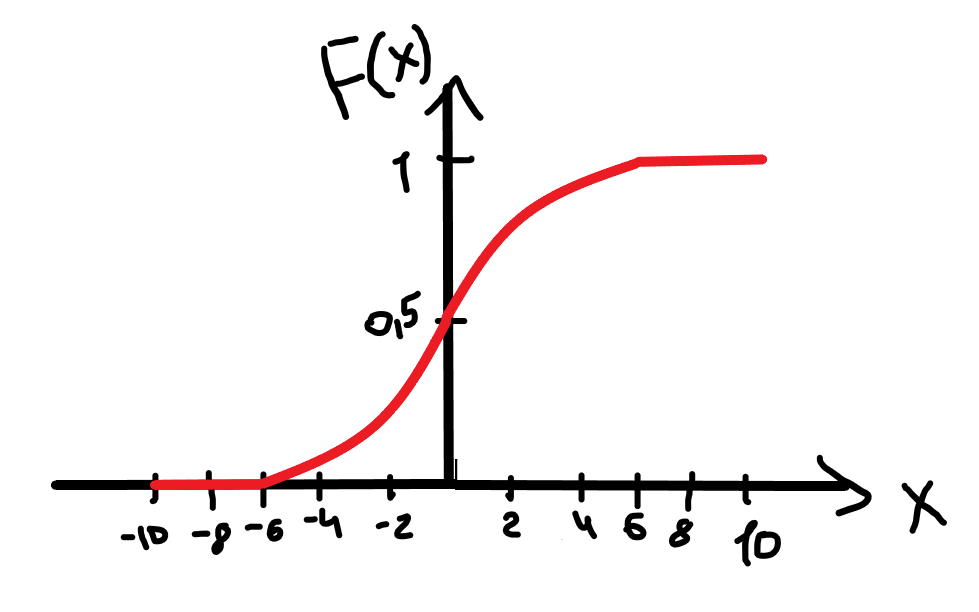 Построим график f(x): 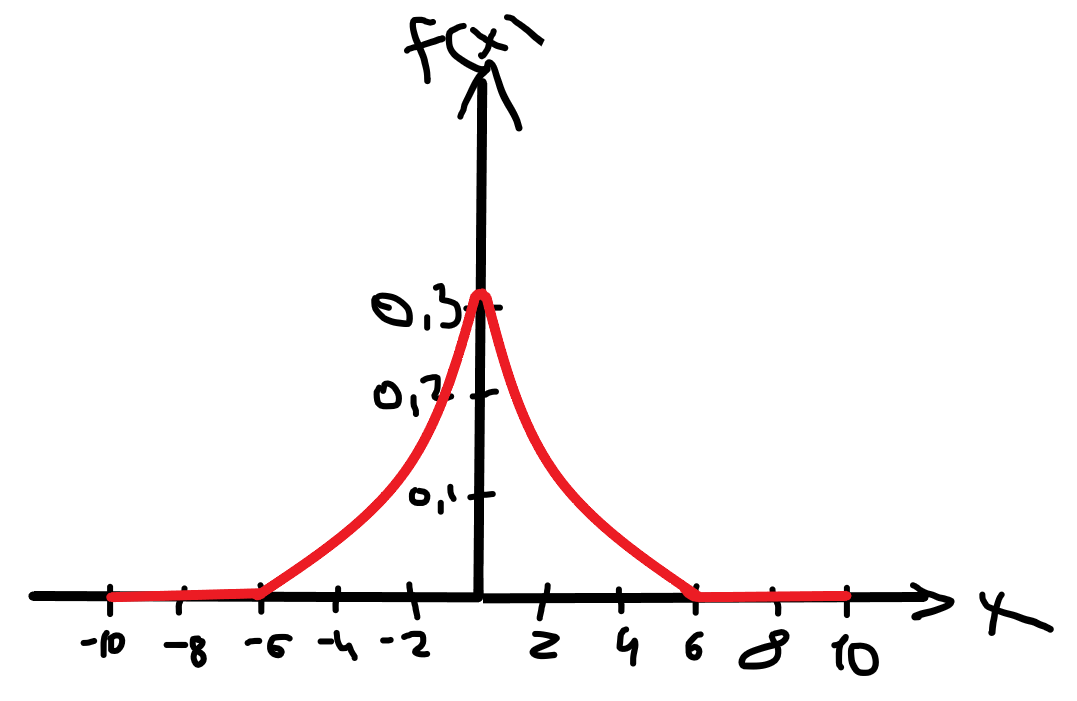 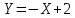
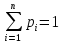 , следовательно, Z находим из уравнения: , следовательно, Z находим из уравнения:0,1+0,6+0,2+Z=1, Z=0,1 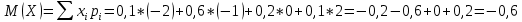 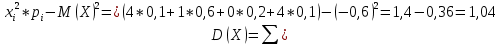 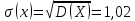 Построим график: 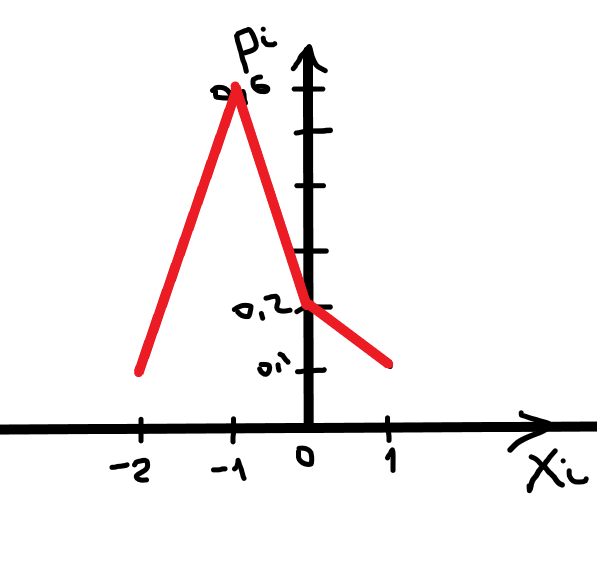 F(x) = 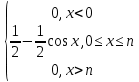 Найдем плотность 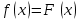 f(x) = 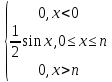 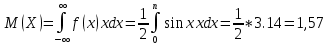 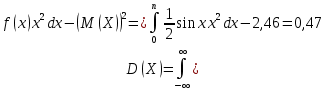 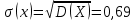 Закон распределения:
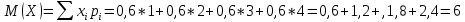 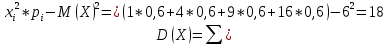 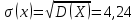 СВ принимает значения 0,1,2,3,4,5,6. Определяем вероятности по формуле Бернулли. 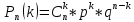 Р(0)=0,000001 Р(1)=0,000054 Р(2)=0,001215 Р(3)=0,01458 Р(4)=0,098415 Р(5)=0,35429 Р(6)=0,53144 Закон распределения СВ имеет вид:
Вычислим F(x). По определению 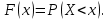 Тогда ТогдаF(x) = 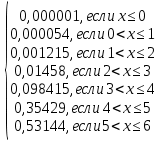 Используем формулу Пуассона: 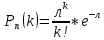 , где л=n*p=2000*0,0005=1 , где л=n*p=2000*0,0005=1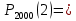 0,185 – откажут ровно 2 элемента 0,185 – откажут ровно 2 элемента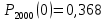 – ни один элемент не откажет – ни один элемент не откажетМенее 3 элементов откажет, т.е 0,1, или 2 Р= 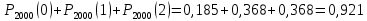 Хотя бы один элемент Р=1- 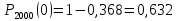 Имеем равномерное распределение на отрезке [0,10]. 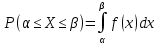 В данном случае, 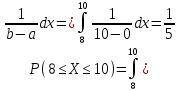 - вероятность ожидания троллейбуса более 8 минут - вероятность ожидания троллейбуса более 8 минут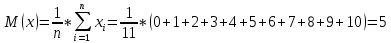 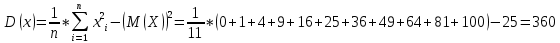 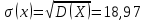 Рассмотрим случайную величину Х – отклонение размера от проектного. Деталь будет признана годной, если случайна величина принадлежит интервалу [-8;8]. Вероятность изготовления годной детали найдём по формуле (см. нормальный закон распределения): 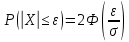 По условию 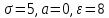 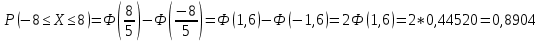 89,04% годных деталей изготавливает автомат.
Коэффициент корреляции: 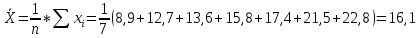 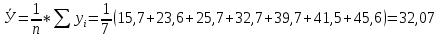 Найдем размах выборки: R=Xmax-Xmin=23,8-0,3=23,5 Рассчитаем шаг (длину интервала): h= R/10=23,5/10=2,35
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
