МУ ПР МДК03.02. По проведению практических занятий

• Название: По проведению практических занятий
• Дата: 09.01.2023
• Размер: 0.71 Mb.
• Имя файла: МУ ПР МДК03.02.docx
• Тип: Методические указания; #878031
• страница: 6 из 22

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1. Специфика контрактных предложений на рынке страхования, позволяющие управлять рисками в цепях поставок

Цель занятия: актуализация теоретических знаний в области контрактных предложений на рынке страхования, позволяющие управлять рисками в цепях поставок и формирование практических навыков расчета

Страхование как метод управления риском получило широкое распространение в связи с так называемым «синергетическим» эффектом диверсификации. Такой эффект возникает в результате синтеза достаточно большого количества предложений. Именно это и происходит, когда страховая компания (за вознаграждение) принимает на себя последствия независимых неблагоприятных событий для большого числа участников рынка.

Суть данного эффекта заключается в том, что совокупный риск, принимаемый на себя страховой компанией, с ростом числа ее клиентов становится в расчете на одного клиента (в среднем) существенно меньше.

Обычно лицо, принимающее решение (ЛПР), располагает предложениями, сформированными страховой компанией на ее условиях, и не может оказывать на них решающего влияния. Тем не менее, для ЛПР важно уметь оценивать эффективность страхования для своего бизнеса и иметь возможность выбирать стратегию, соответствующую его отношению к риску. Предложения страховой компании формализуются, как известно, с использованием следующих характерных параметров:

• 
  С - стоимость страхового полиса, которую страхователь при заключении страхового контракта заплатит страховой компании (в качестве компенсации за риск, принимаемой ею на себя);
  
• 
  h - коэффициент возмещения, показывающий какая компенсация полагается ЛПР на каждый рубль стоимости страхового полиса при наступлении страхового случая;
  

-- P = С·h - величина страхового возмещения, выплачиваемая страховой компанией ЛПР при наступлении страхового случая.

Предположим, что в формате анализа процедур некоторого звена цепи поставок ЛПР планирует заключить сделку, которая предполагает вложение капитала на сумму S.

Ожидается, что при благоприятном развитии событий он получит сумму

(1+r)·S,

где r - норма прибыли для сделок такого рода.

При этом для упрощения модели и удобства интерпретации пусть учитываются только два сценария:

1. 
   события могут развиваться благоприятно; вероятность этого обозначим через p; при этом страховой случай не наступит и экономический результат будет определяться суммой (1+r)·S;
   
2. 
   соответственно, с вероятностью q = 1-p события будут развиваться неблагоприятно; при этом наступает страховой случай, а экономический результат для выручки от самой сделки (без учета предложения страховой компании) будет нулевым.
   

Пусть, снова для упрощения модели ЛПР анализирует именно две альтернативы:

• 
  А1 - совершить сделку без страхования;
  
• 
  А2 - воспользоваться конкретным предложением страховой компании при известных параметрах C и h (например, при максимальном покрытии риска в формате обсуждаемой сделки).
  

Рассмотрим данную ситуацию, структурируя ее виде дерева решений на рис. 1.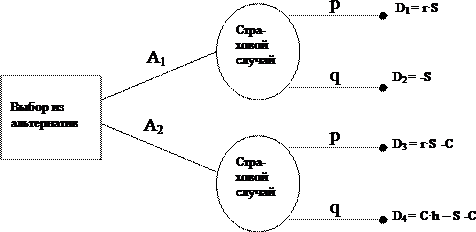



Рис. 1. Дерево решений при страховании
Как видно на рис. 1, применительно к альтернативе А1 (в ситуации без страхового контракта) при благоприятном стечении обстоятельств ЛПР получит в виде выручки, как и ожидал, сумму
D1 = (1+r)S,
где D1 – выручка в ситуации без страхового контракта при благоприятном развитии событий, т.е. без страхового случая.

При неблагоприятном развитии событий без страхового контракта (в случае наступления страхового случая) ЛПР потеряет вложенную сумму S и конечный результат выручки составит D2 = 0.

Применительно к альтернативе А2 приобретение страхового полиса дополнительно требует вложения суммы C. При этом без наступления страхового случая выручка ЛПР составит сумму

D3 = (1+r)·S – C,

где D3 – выручка ЛПР в случае приобретения страховки и без наступления страхового случая; C – стоимость страхового полиса;

r - норма прибыли.

При наступлении страхового случая из-за наличия страховки ЛПР полагается страховое возмещение: в итоге сумма выручки составит

D4 = C·h,

где D4 – выручка ЛПР в случае приобретения страховки и наступления страхового случая; C – стоимость страхового полиса;

h - коэффициент возмещения.

Владея методом дерева решений, ЛПР при конкретном отношении к риску всегда может самостоятельно определить, целесообразно ли приобретать страховой полис при известных параметрах (и на какую сумму денежных средств его приобретать). Тем не менее, для ЛПР еще до того, как станет известна цена страхового полиса, важно уметь определять безрисковую стратегию

и рентабельность¹, полагая их как исходные эталонные точки отсчета для дальнейших рассуждений.

В рассмотренной ситуации найдем условия, когда ЛПР при помощи страхового контракта может полностью исключить для себя те риски, которые страховая компания берет на себя. Нетрудно убедиться в следующем. Безрисковый для ЛПР результат в указанной ситуации возможен тогда и только тогда, когда будет выполнено равенство:
D1 = D4 .
Указанное равенство перепишем в виде:
(r+1) · S = C·h .
Действительно, ЛПР полностью исключит указанные риски при равенстве следующих конечных экономических результатов

1. 
   без страховки для случая благоприятного развития событий;
   
2. 
   со страховкой при наступлении страхового случая с учетом соответствующего страхового возмещения.
   

Если такое равенство имеет место, то при наступлении неблагоприятного события ЛПР ничего не теряет и получает ровно столько, сколько соответствует благоприятному результату. При этом возможно определить и стоимость страхового полиса, обеспечивающего такие условия для ЛПР при известном коэффициенте страхового возмещения. А именно, находим показатель С из равенства:
(r+1) · S = C · h.
Это равенство можно записать в виде:
С = (1 + r) S / h.
Страхование на условиях полного исключения риска и составляет безрисковую стратегию ЛПР (в формате рисков, которые страховая компания берет на себя). При этом управление риском требует затрат, которые в данном случае совпадают со стоимостью страхового полиса, что отразится и на безрисковой рентабельности. Соответственно, если максимально возможная (в расчете на везение) рентабельность при стратегии без страхования² характеризуется множителем 1+r при анализируемом преобразовании исходного капитала

S > S · (1 + r),

¹ Рентабельность показывает, сколько прибыли приносит каждая вложенная единица денежных средств.

² Если при вложении суммы S в сделку с нормой прибыли r предприниматель в безрисковом случае получит обратно свою вложенную сумму S и прибыль, равную Sr, или (1+r)·S, то рентабельность такой сделки равна отношению


S
^{1r·S} , или при сокращении дроби – множителю (1+r).

^{то безрисковая рентабельность характеризуется соответствующим множителем (1+r}0^{), где r}0 ^{– норма прибыли в случае безрисковой сделки. Безрисковая рентабельность (1+r}0^{) определяется} отношением суммы, полученной ЛПР в результате наступления страхового случая (страхового возмещения Р), к суммарным затратам (S + C):
^{1 + r}0 ^{= Р / (S + C) = C · h/(S + C) = (1 + r)h/(h + r + 1).}
Проиллюстрируем соответствующие выводы численными расчетами. Это позволит сравнить ^{порядок величин 1 + r и 1 + r}0^.

Пример 1. Компании, специализирующейся в области производства лекарственных средств, предложен контракт на сумму 150 тыс. у.е. на изготовление нового лекарства. Необходимое фармакологическое сырье (далее субстанция) предполагается закупить в Китае (при условиях доставки до российской таможни за счет китайских партнеров). Стоимость данной субстанции составляет 100 тыс. у.е.

Требуется найти безрисковую рентабельность, если стоимость страхового полиса составляет 0,5% от величины страхового возмещения (коэффициент возмещения h = 200).

Решение

При стоимости контракта 150 тыс. у.е. стоимость страхового полиса в таких условиях составит 0,75 тыс. у.е., соответственно.

^{Безрисковую рентабельность (r}0^{) находим по формуле:
1 + r}0 ^{= C · h / (S+C) = (0,75*200)/(100+0,75) = 1,489}
Соответственно, норма прибыли для безрисковой сделки составит:

^r0 ^{= 0,489 .}
При этом рентабельность предложения в расчете только на «везение» и благоприятный исход составит r+1 = 150/100 = 1,5, откуда норма прибыли при стратегии без страхования r = 0,5.

Таким образом, решая вопрос страховать доставку или нет, ЛПР по сути выбирает между следующими альтернативами:

• 
  с одной стороны, в формате альтернативы А1 ЛПР может надеяться или рассчитывать только на везение. При этом норма прибыли сделки составит 50% (если повезет). Но в этой же ситуации рентабельность может составить и -100% (потеря вложенного капитала, если не повезет).
  
• 
  с другой стороны, в формате альтернативы А2 ЛПР может обеспечить норму прибыли 48,9% при любом исходе сделки. Соответственно, риск будет исключен.
  

Как видим, за исключение риска надо «платить» некоторым снижением гарантированной нормы прибыли: 48,9% вместо возможных (если повезет) 50%, то есть уступим 1,1% в прибыли за исключение риска.

Какая альтернатива лучше? Выбор всегда за ЛПР.

Другим способом безрисковую рентабельность можно было получить из приведенного выше равенства:

^{1 + r}0 ^{= (1+r)h/(h+r+1) = (1+0,5)*200/(200+0,5+1) = 1,489 .}
Соответственно, имеем тот же результат:

^r0 ^=0,489.
Таким образом, зная параметры страхового контракта можно оценить безрисковую рентабельность предложения при использовании метода страхования рисков. Это поможет оценить и «плату» за исключение риска. Дальнейшее решение зависит от отношения ЛПР к риску. В данном примере рассматривались только два сценария – благополучный исход и крайне неблагополучный. При этом при неблагополучном исходе предполагалось, что происходит потеря всей партии товара, что требует и выплаты всей суммы страхового возмещения. На практике страховое возмещение по контракту может быть пропорционально доле потерянного товара. Такое

условие может быть учтено при введении дополнительных сценариев.

Рассмотрим решение некоторых задач.