вычеслительная математика. Вычеслительная математика. Почта
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
10.01.2022
Лекция 1(конспект) Вычислительная математика Концепция итерационных вычислений в вычислительной математике на примере: Решение алгебраических и трансцендентных уравнений В практике вычислений приходится решать уравнения вида f(x) = 0, где f(x) определена на некотором конечном или бесконечном интервале (a, b). Если f(x) — многочлен, то f(x) =0 — алгебраическое уравнение, иначе f(x) = 0 — трансцендентное уравнение. Всякое значение x* такое, что f(x*) Этапы решения: Отделение корней, то есть отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения. Вычисление корней с заданной точностью. Комментарий 1. Для выделения областей, в которых находятся действительные корни уравнения, можно воспользоваться тем, что если на концах отрезка непрерывная функция f(x) принимает значение разных знаков, то на этом отрезке f(x) = 0 имеет хотя бы один корень. Для выделения областей, содержащих один и только один корень можно воспользоваться, например, графическим способом. Комментарий 2. Для решения 2-й задачи существуют многочисленные методы: метод итераций, метод Ньютона, метод половинного деления и т.д. Считаем, что нам известен отрезок Уравнение f(x) =0 представим в виде x = В общем случае: Выберем на отрезке x1= x2= … xn= Процесс последовательного вычисления чисел xn (n=1, 2, …) по формуле xn= Если на Процесс итераций следует продолжать до тех пор, пока для 2-х последовательных приближений xn-1 и xn не будет обеспечено выполнение неравенства Если g Итак, | Действительно : пусть x* — корень, то есть x* = xn = xn-x* = xn-x* = 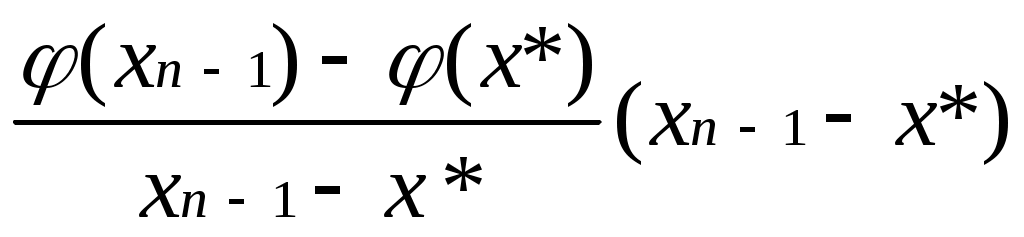 Используем теорему о среднем значении: если Или Пусть m = max  | xn-x* | | xn-x* || xn-1-x* |  | xn--x* | | xn--x* || xn-x* | Если k = n, то | xn--x* | Если m<1, то с ростом n: xn При | 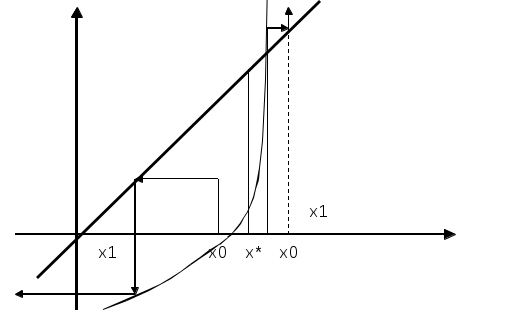 расходится расходится 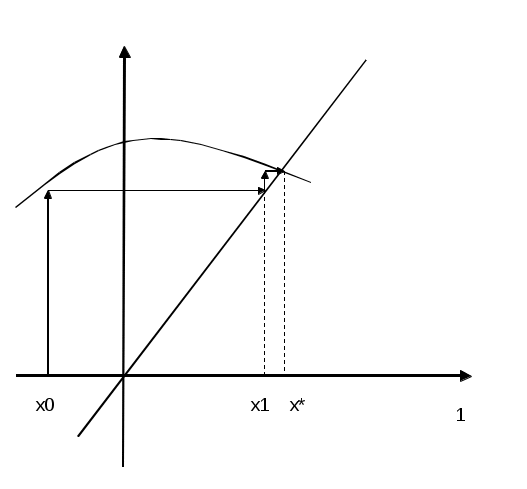 сходится сходится 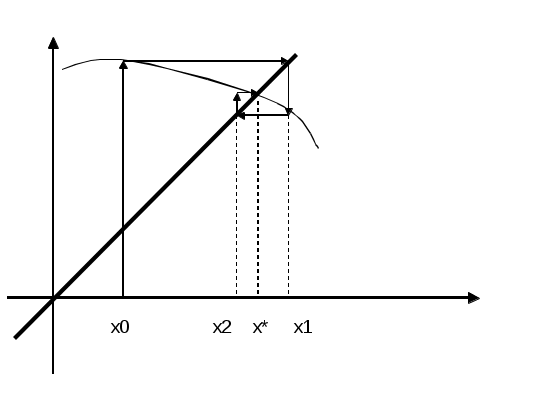 сходится сходится 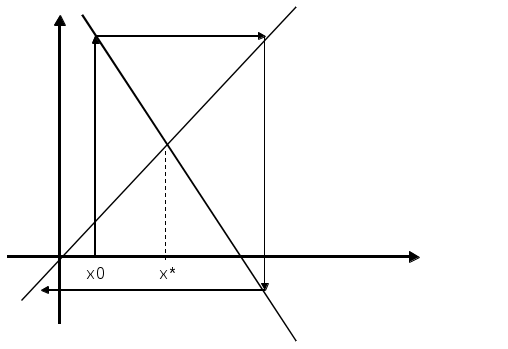 расходится расходится Для приведения уравнения к виду x = Пусть 0<m1 M1 = max f’(x) на [ (если f’<0, то вместо уравнения f(x) = 0 рассматриваем уравнение –f(x) = 0). Заменим уравнение f(x) = 0 эквивалентным ему уравнением x = x - П  одберем параметр одберем параметр Пример: Sin·x + 0.25 – x = 0 f(x) = Sin·x + 0.25 – x = 0; Так как x = Пусть x0 = 1.2; 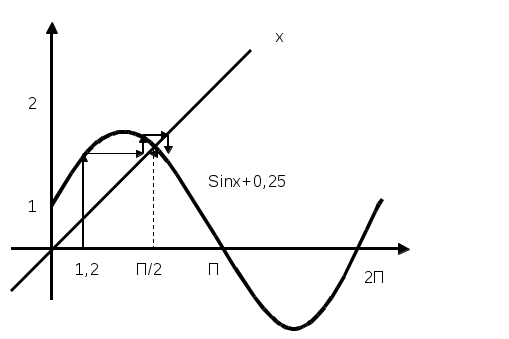 Function Sinus (t) Sinus = Sin (t) + 0.25 End Function ' /—//—//—//—//—//—//—// Sub Itera () Dim fi As Single Dim x As Single x = CSng( InputBox (“Задайте начальное приближение”) Metka: fi = sinus (x) if abs ( x- fi) < = 0.000001 then MsgBox (x, 1, “Решение”) : goto Metka_1 End if x = fi goto Metka Metka_1: end Sub 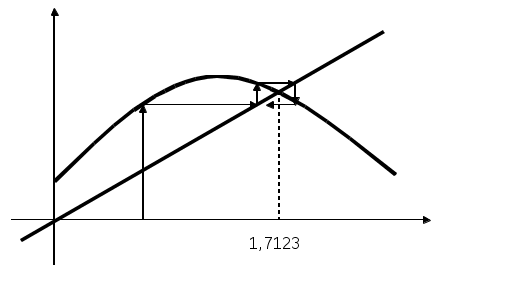 Метод Ньютона – Рафсона 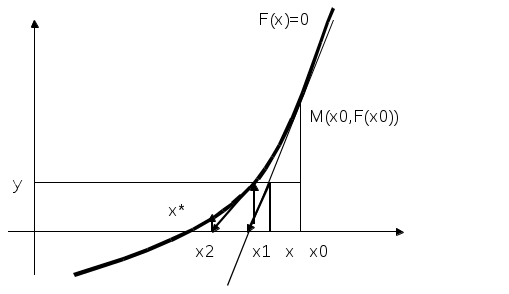 Уравнение имеет вид F(x) = 0 Запишем уравнение касательной к F(x) в точке x0: tg y = F(x0) + F'(x0)(x-x0) Пусть y = 0 x2 = x1- … xn = xn-1- |xn- xn-1 | < M2 = max F''(x) на [ x0 выбирается так, что F(x0) · F''(x0)>0 Пример: 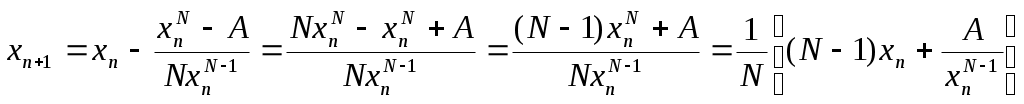 N = 2; N = 3; Или Лекция 2 (конспект) Вычислительная математика (Методы) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
