вычеслительная математика. Вычеслительная математика. Почта
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
(для нелинейных алгебраических и трансцендентных уравнений) Усовершенствованный метод последовательный приближений 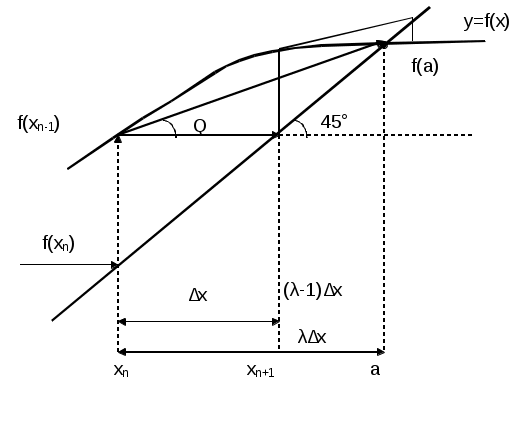 f(xn-1) = xn; f(xn) = xn+1 ∆x = xn-1 – xn = f(xn) - xn xn+1 = xn + ∆x, лучше взять xn+1 = xn + λ *∆x, λ>1 tg t 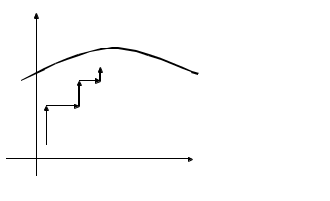 g gf'( f'( Геометрический процесс отыскания следующего приближения xn-1 сводится к тому, что проводится хорда через точки (xn, f(xn)) и (xn-1, f(xn-1)) и определяется точка ее пересечения с прямой y = x. Сходимость: 1) 0<f'(x)<1 поправки ∆x малы, но 1< 2) -1 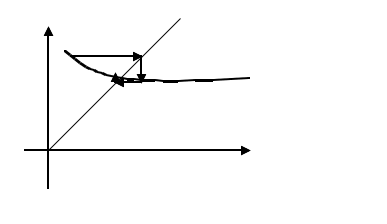 поправки велики, а Расходится: 3) f'(x)>1 Т 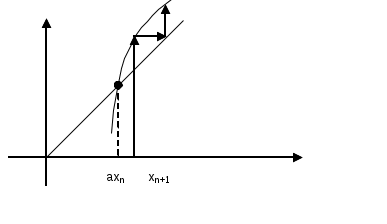 ак как ак как 4) f'(x)<-1 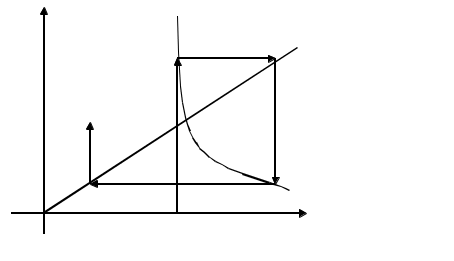 Каждая поправка умножается на коэффициент между 0 и Описанная модификация метода итераций принадлежит Векштейну (1958 г) Метод Ньютона – Рафсона Пусть xn Если 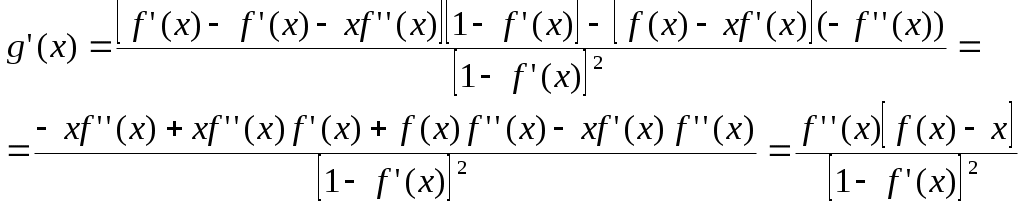 Так как f (x) = x, (F (x) = 0 = x – f (x)), то для x, близких к «a», (f (x) - x) – мало. Поэтому (1) сходится, если: 1) 2) f ''(x) – не становится слишком большой. 3) f ' (x) не слишком близка к 1. Это и есть знаменитый метод Ньютона – Рафсона. Или: 1) 2) 3) «3)» означает, что никакие два корня не находятся слишком близко один к другому. Геометрическое толкование. а) 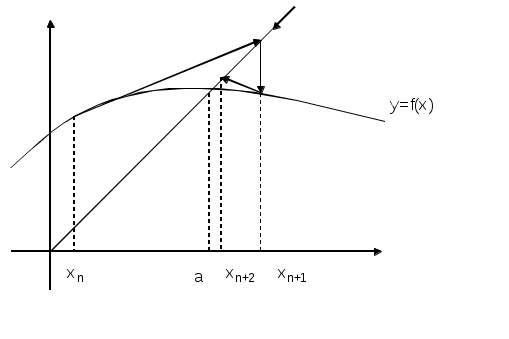 б) 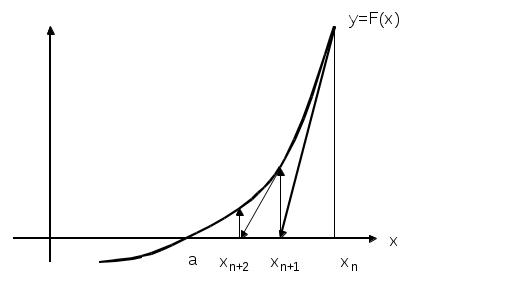 Уравнение касательной: Пусть 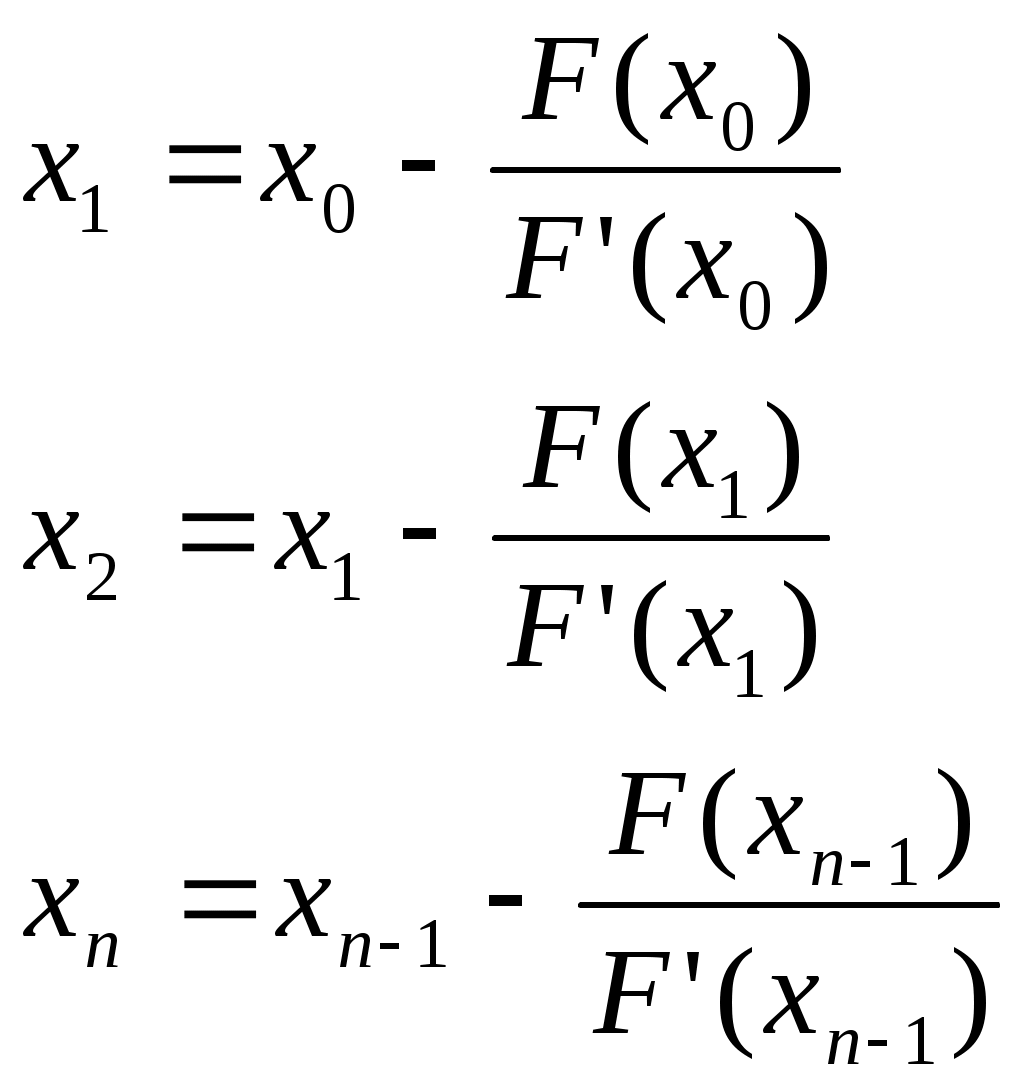 Пример: F (x) = sinx – x + 0.15 = 0 на отрезке [0.5; 1] с погрешностью 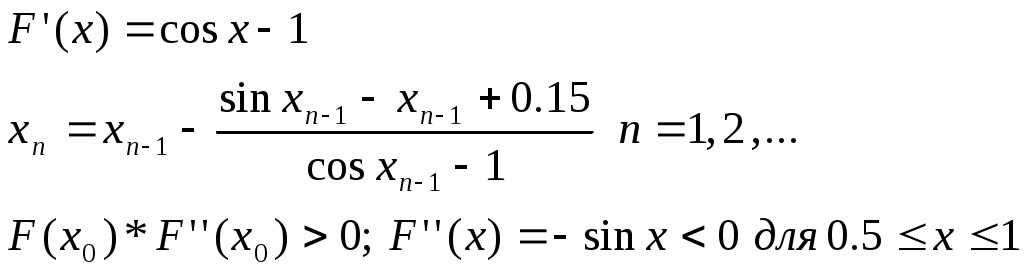 То необходимо найти Это верно при 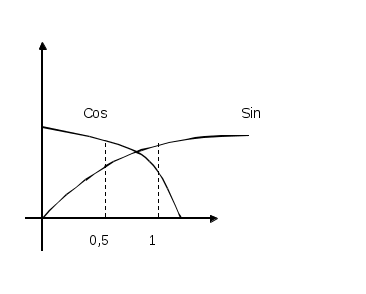 Примечание: если 1) 2) 3) Вычисляем 4) Проверяем Случай почти равных корней 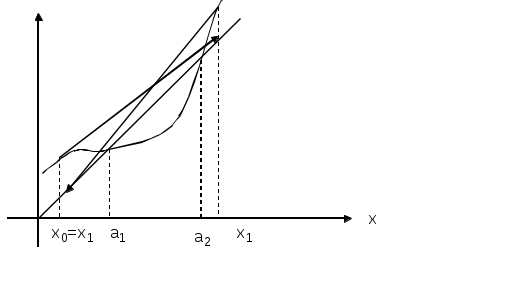 (Масштаб сильно увеличен: на самом деле х0 очень близок к х1 ) Производная На основании теоремы о среднем 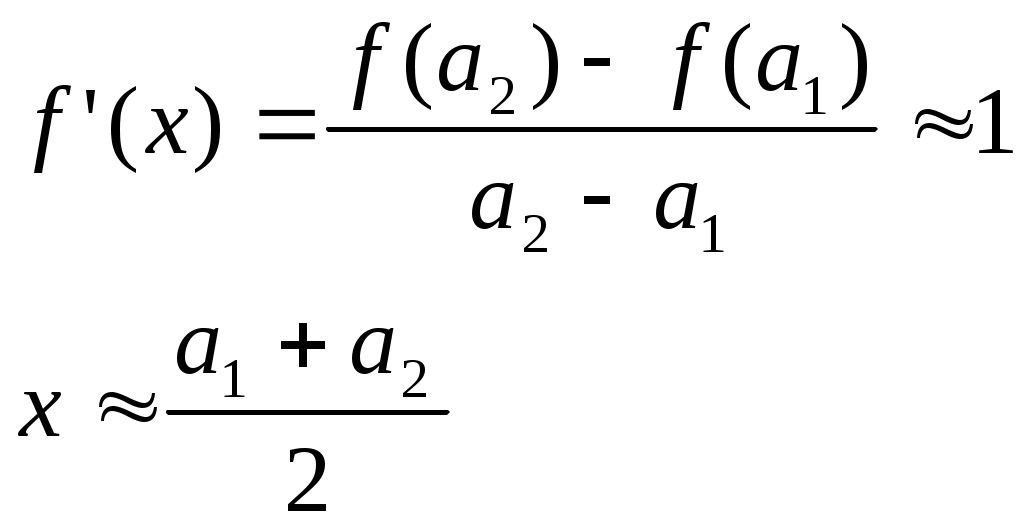 Итерационный процесс осциллирует (колеблется) между Трудности возникают, так как Мейкон (1963) предложил метод, согласно которому сначала находят значение x, где Пусть Положим для начального приближения Пусть Разложим f (x) в ряд Тейлора в окрестности точки Так как Пусть Но по условию 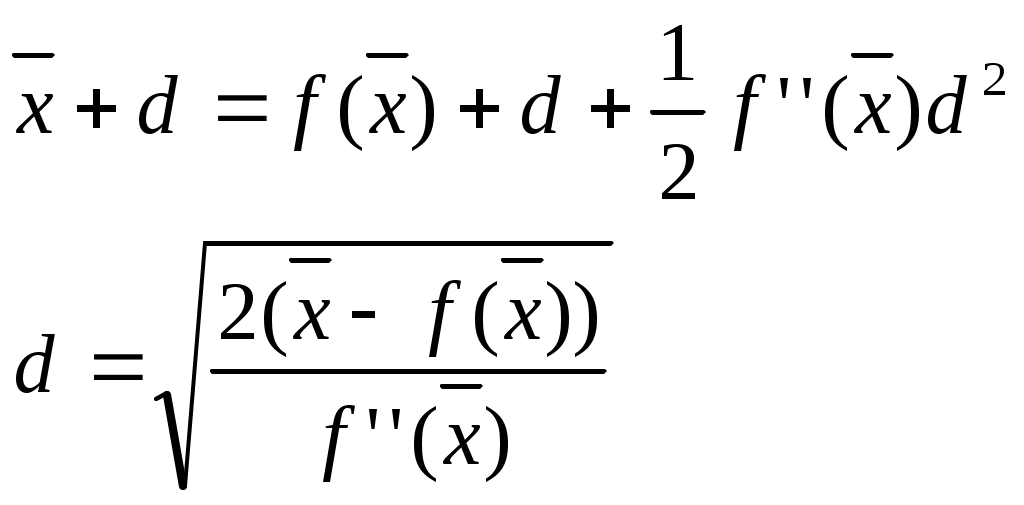 Если 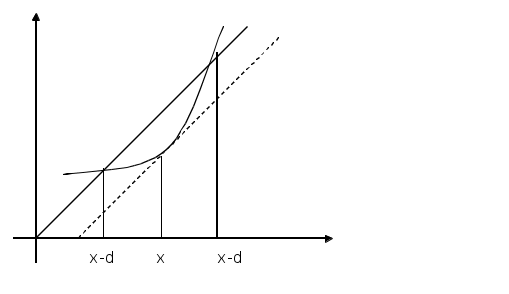 Сначала решаем: Потом ищется: Затем начальные приближения для Если Метод хорд Каждое значение xn+1 находится как точка пересечения оси абсцисс с хордой, проведенной через точки F(a) и F(b) , причем одна из этих точек фиксируется — та, для которой F(x)·F''(x)>0. Если неподвижен конец хорды x = a, то xn+1 = xn - Если неподвижен конец хорды x = b, то xn+1 = xn - Если |xn+1 - xn|> При использовании метода хорд полагается, что корень 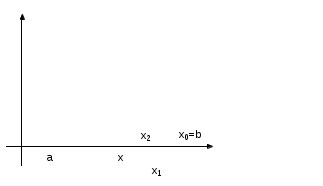 Метод секущих (графическая иллюстрация) |
