вычеслительная математика. Вычеслительная математика. Почта
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
Реализуется алгоритмом, описанным выше, если абсцисса a и b взяты с одной стороны от корня. Необходимость вычисления F'(x) и выбора одной из двух формул затрудняют практическое применение методов хорд и секущих в отдельности. 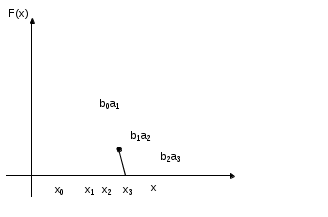 Примечание. Студент выбирает вариант задания по своему № в списке таблицы с электронными адресами. Если номер больше, чем Ваш № в списке, то надо сложить цифры своего двузначного номера и взять задание с полученным таким образом №. ЗАДАНИЯ (для КР и зачёта) Отделить корни уравнения графически (используя мастер диаграмм среды Excel 2000) и уточнить один из них методом итераций (используя среду VBA для Excel 2000 и «выше») с точностью до 0,001. Вариант №1 Вариант №2 Вариант №3 Вариант №4 Вариант №5 Вариант №6 Вариант №7 Вариант №8 Вариант №9 Вариант №10 Вариант №11 Вариант №12 Вариант №13 Вариант №14 Вариант №15 Необходимо вычислить приближенное значение корней уравнения с заданной точностью методом итераций и методом Ньютона-Рафсона. Необходимо построить график y(x) для этих уравнений, отделить корни на соответствующих отрезках.
Решение систем линейниых (СЛАУ) и нелинейных уравнений (СНАУ) Метод Ньютона - Рафсона для систем нелинейных уравнений Будем искать решение системы нелинейных уравнений 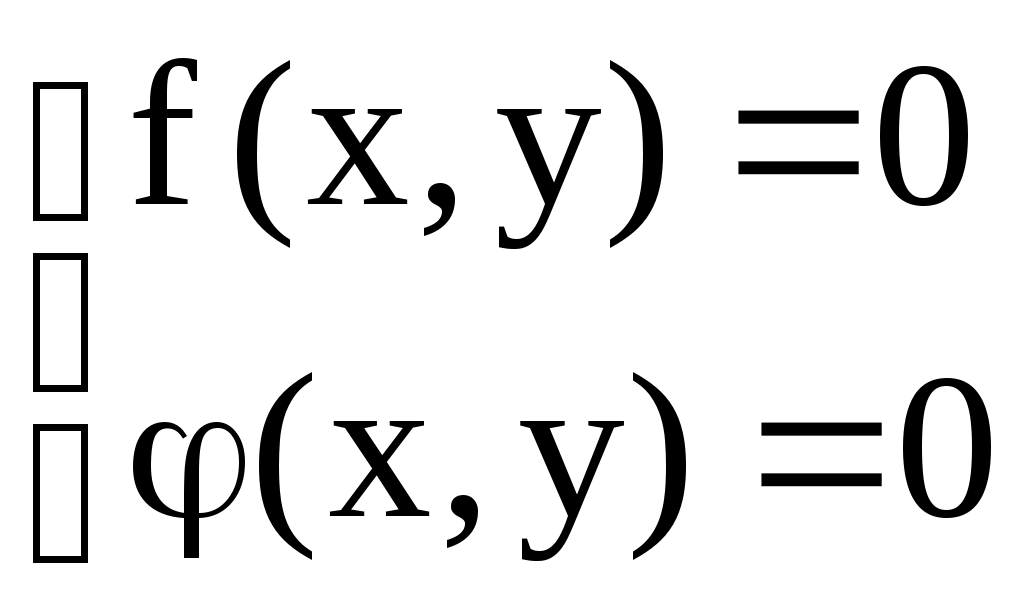 . .Считая заданными начальные приближения корней (x0, y0), будем искать поправки к ним h и k: 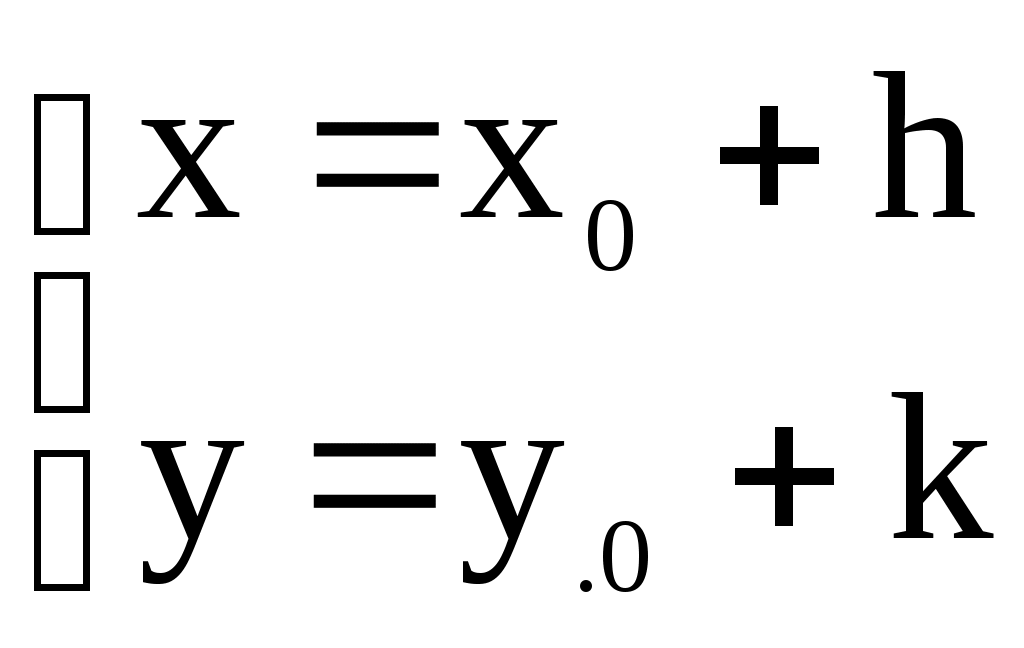 или в общем виде или в общем виде 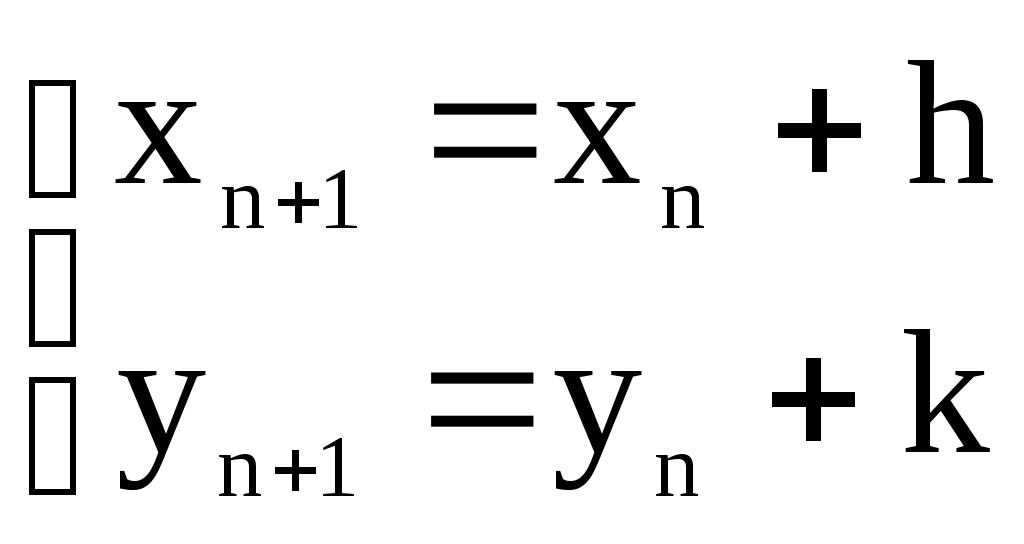 . .Таким образом, имеем систему:  Раскладывая функции в ряд Тейлора, имеем: 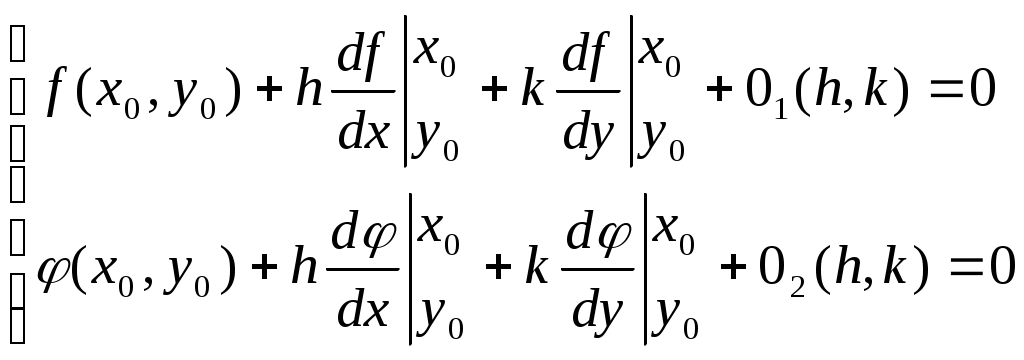 Уравнения системы содержат члены более высокого порядка малости, чем h и k. Пренебрегая ими, получим систему относительно h1 и k1: 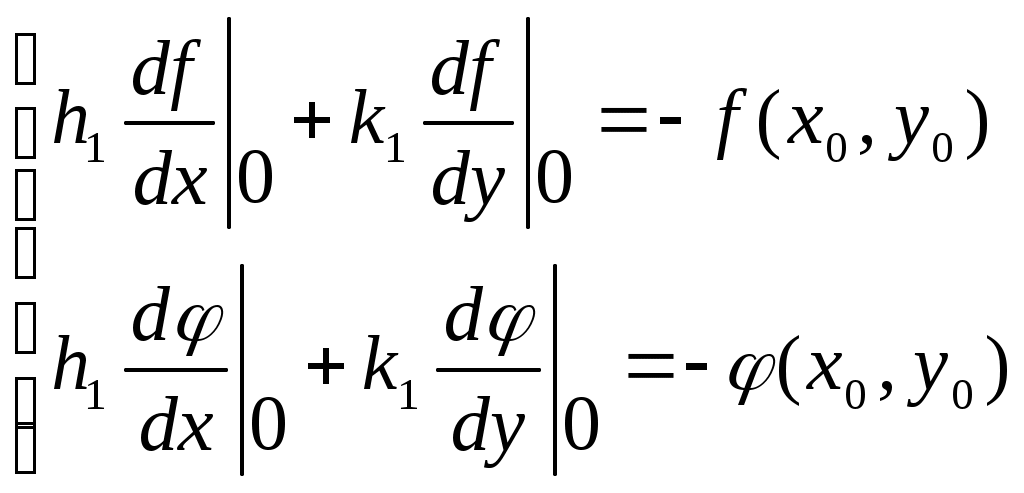 Отсюда 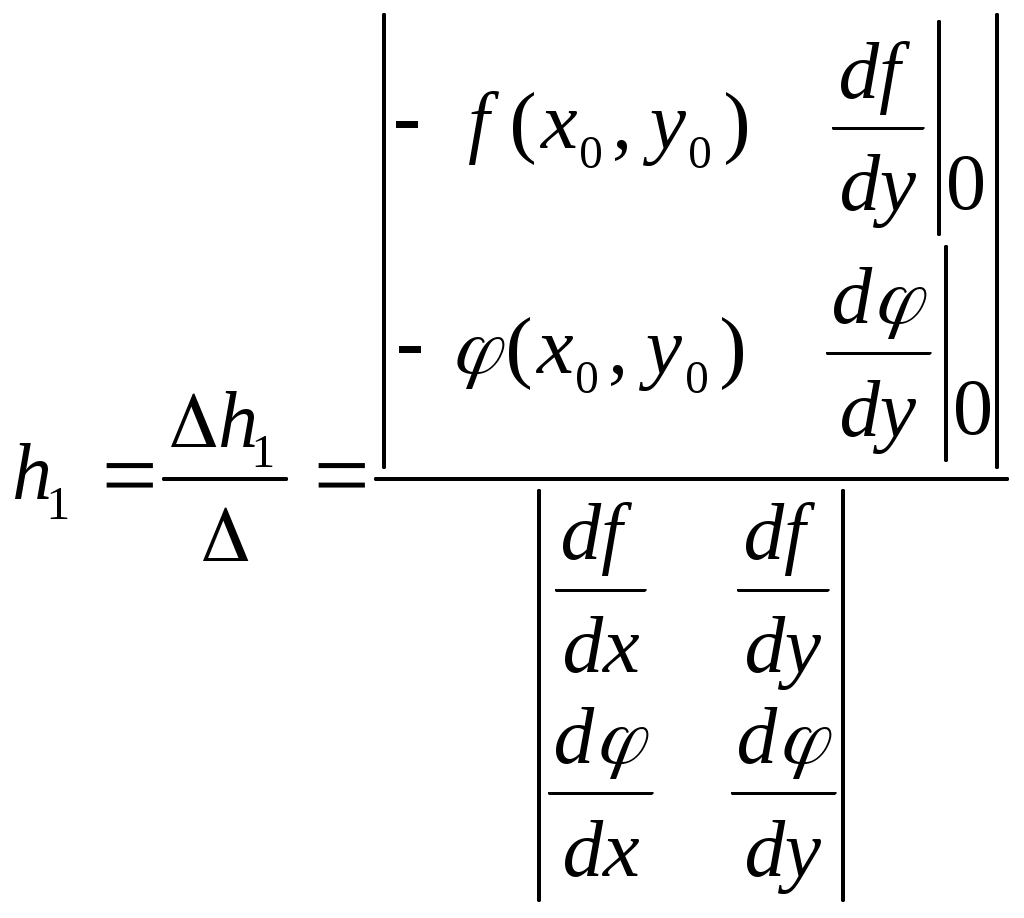 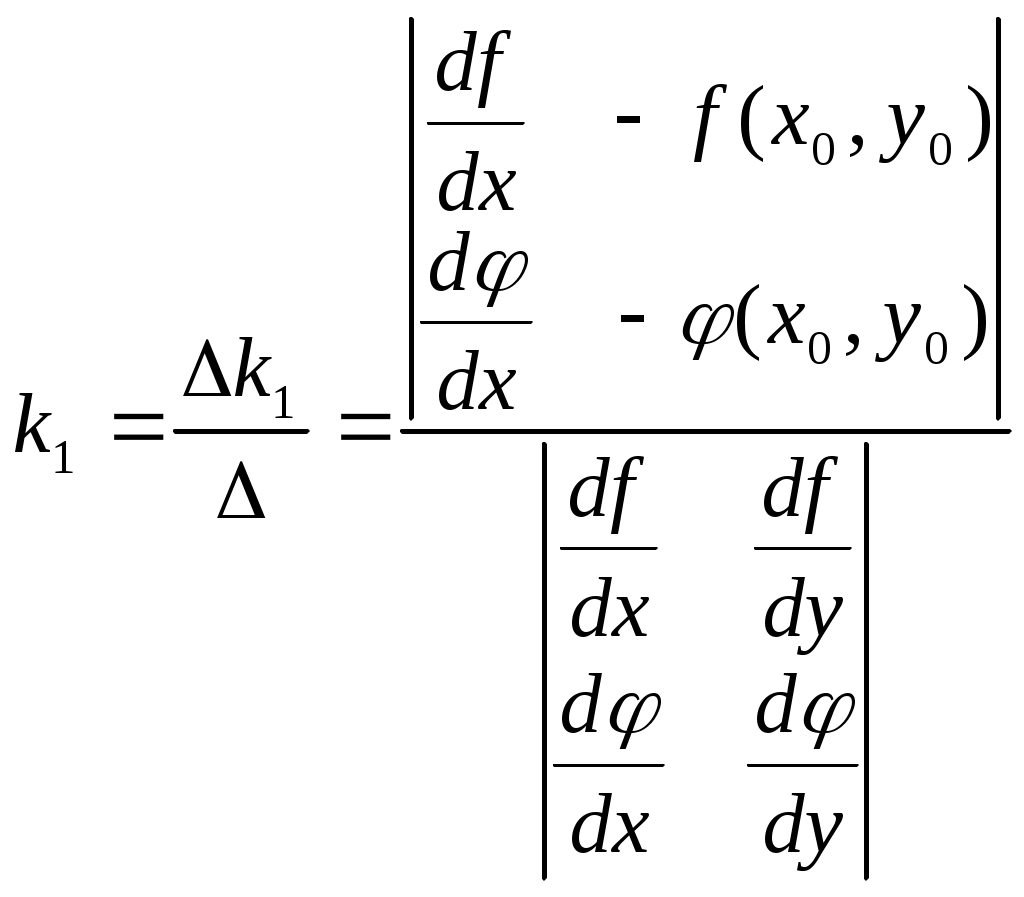 Тогда Пример. Найти корни системы уравнений: 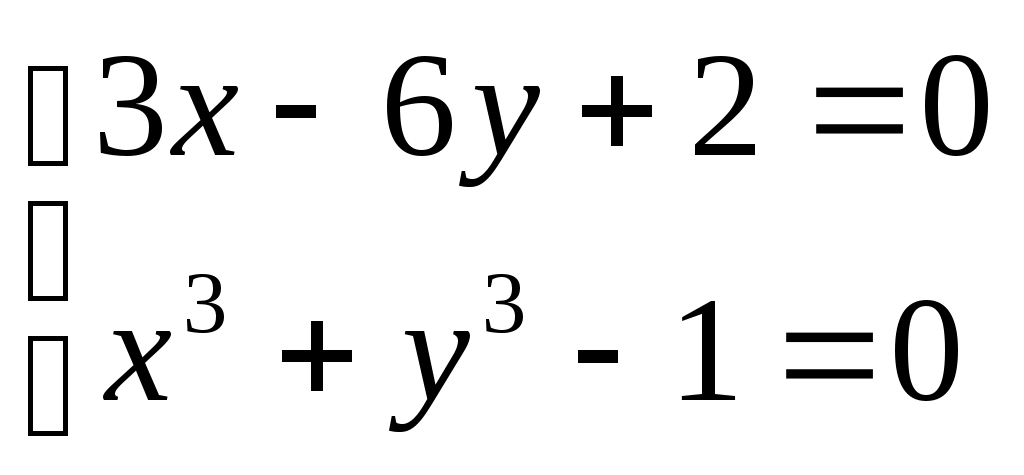 Пусть 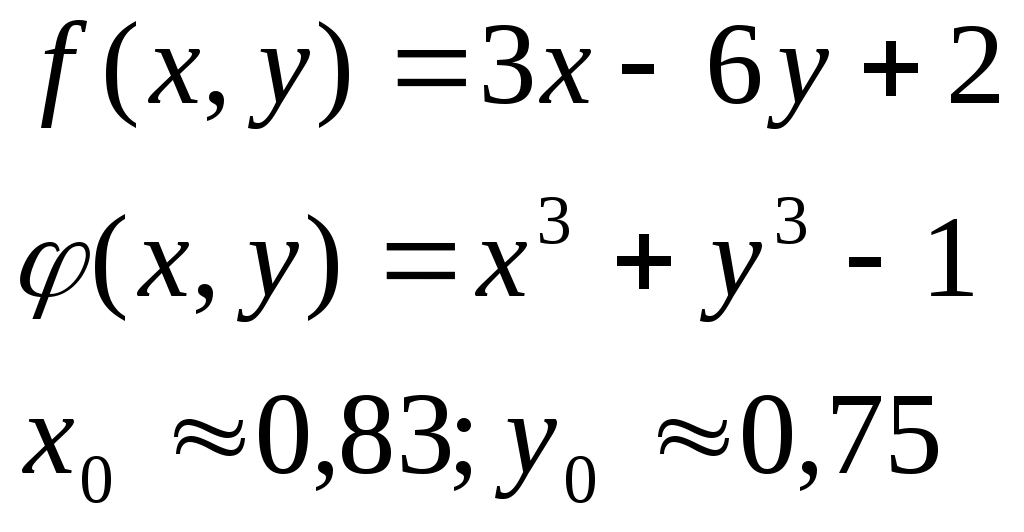 Тогда 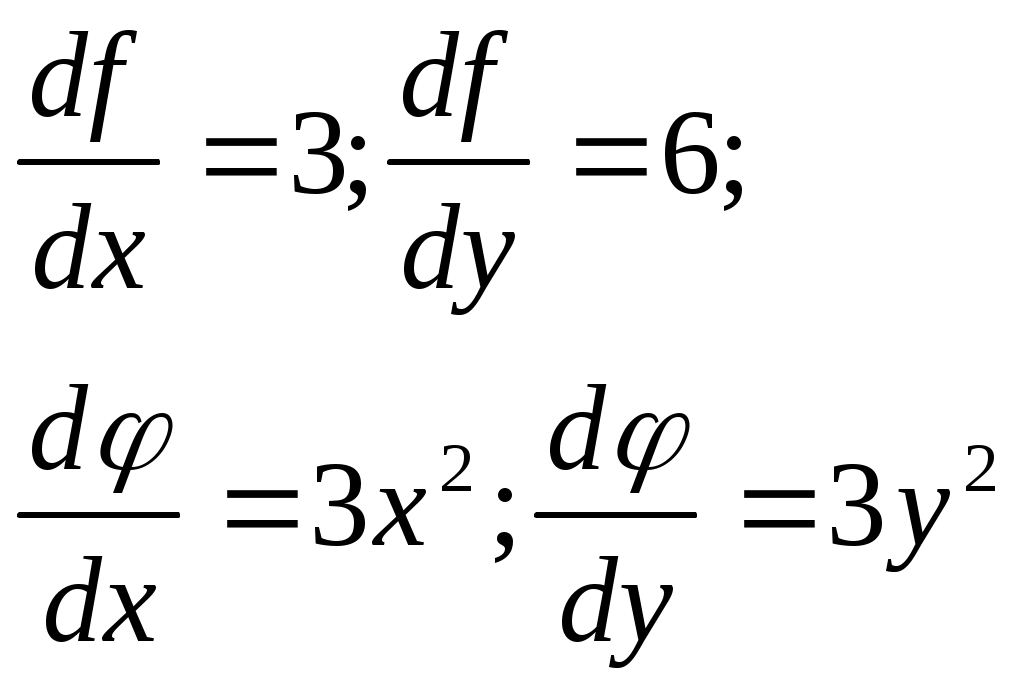 Получаем 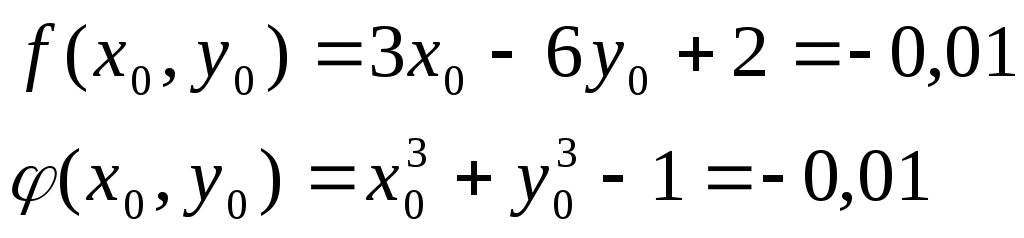 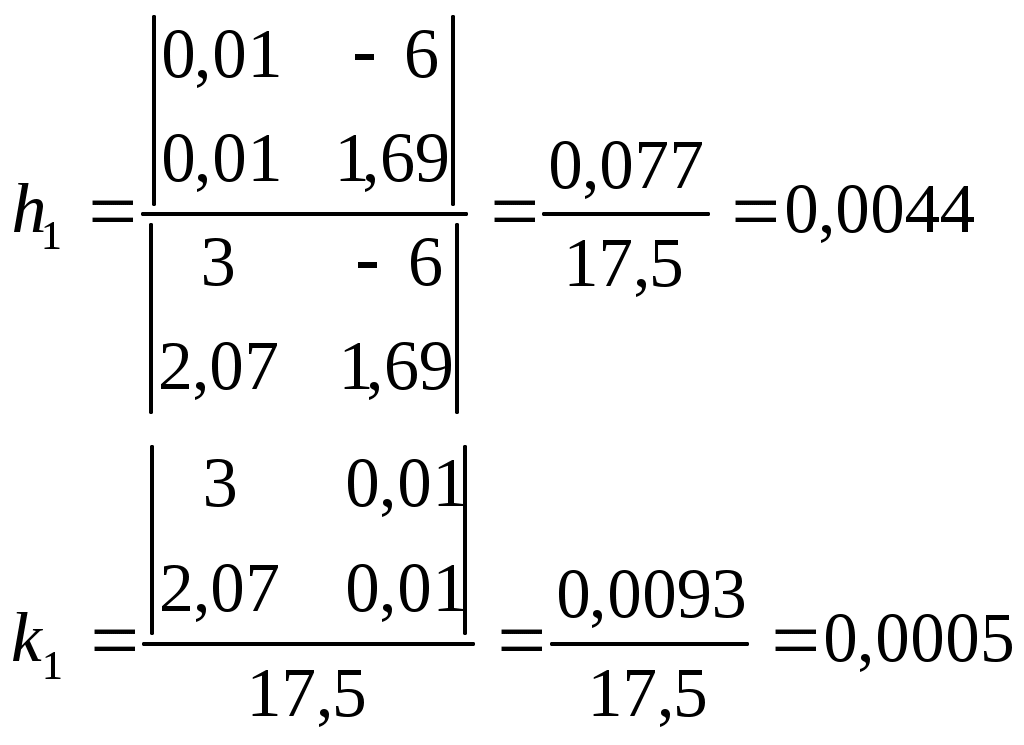 Метод итерациЙ для систем нелинейных уравнений Пусть дана система уравнений с двумя неизвестными: 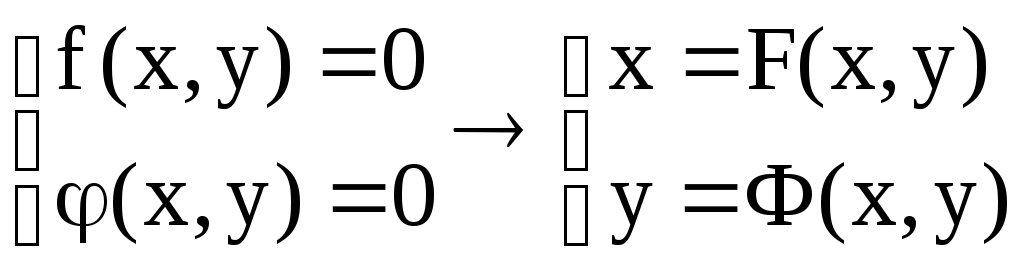 . .Функции 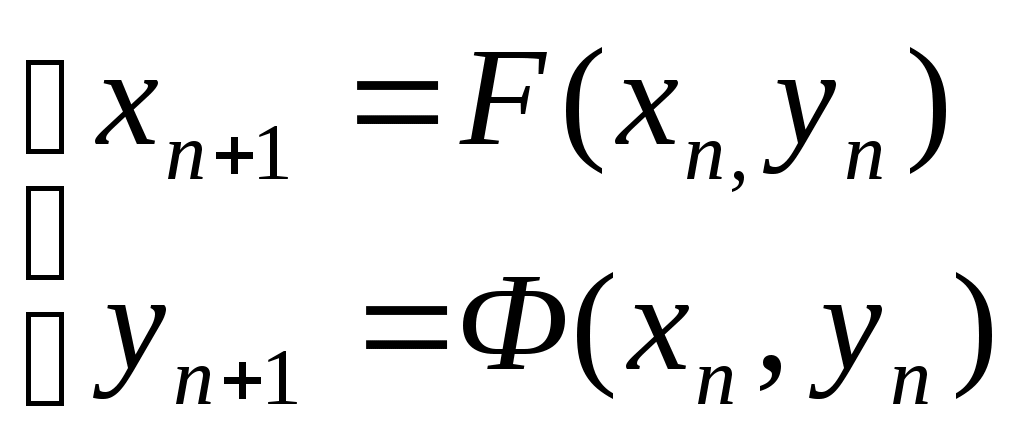 Если функции F (x, y) и Ф (x, y) непрерывны и последовательности Исследуем сходимость. Пусть Где Пример. 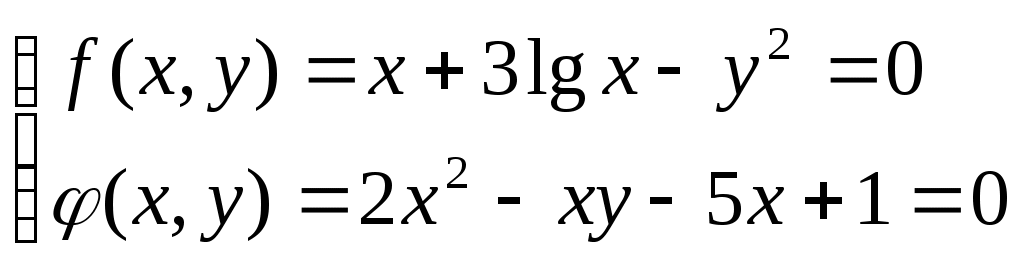 Рассмотрим точку x0 = 3,4; y0 = 2,2 Приведём систему (различными путями) к виду: 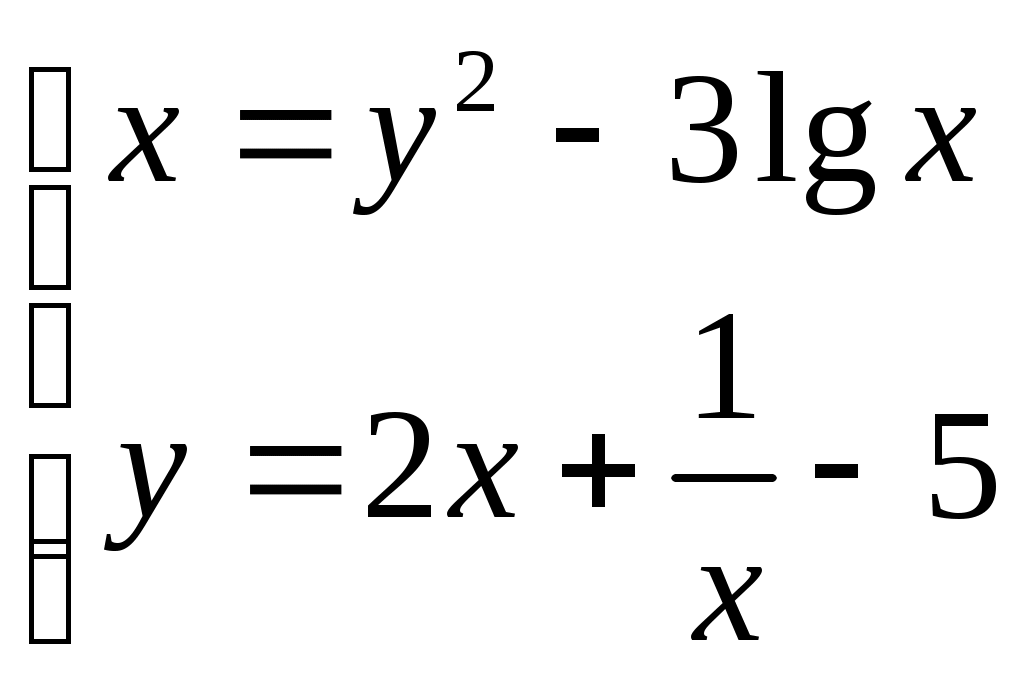 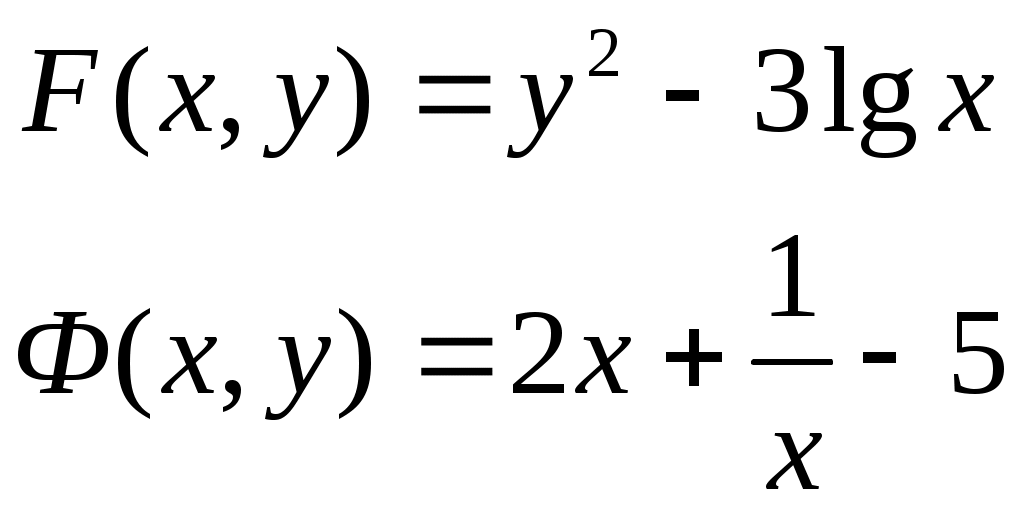 Для Поэтому, определим x из 2-го уравнения; y — из 1-го: 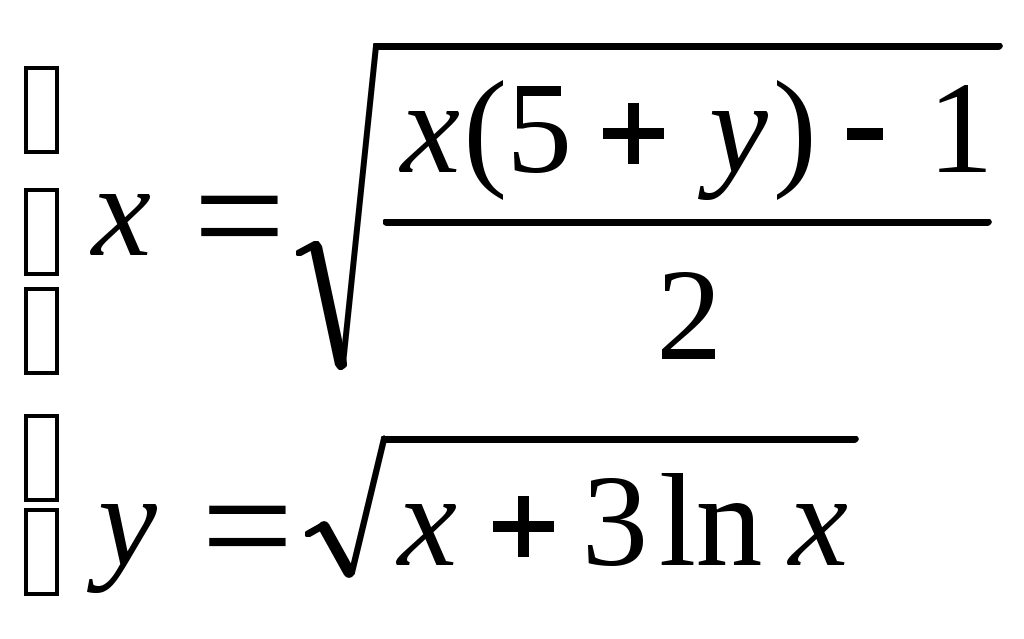 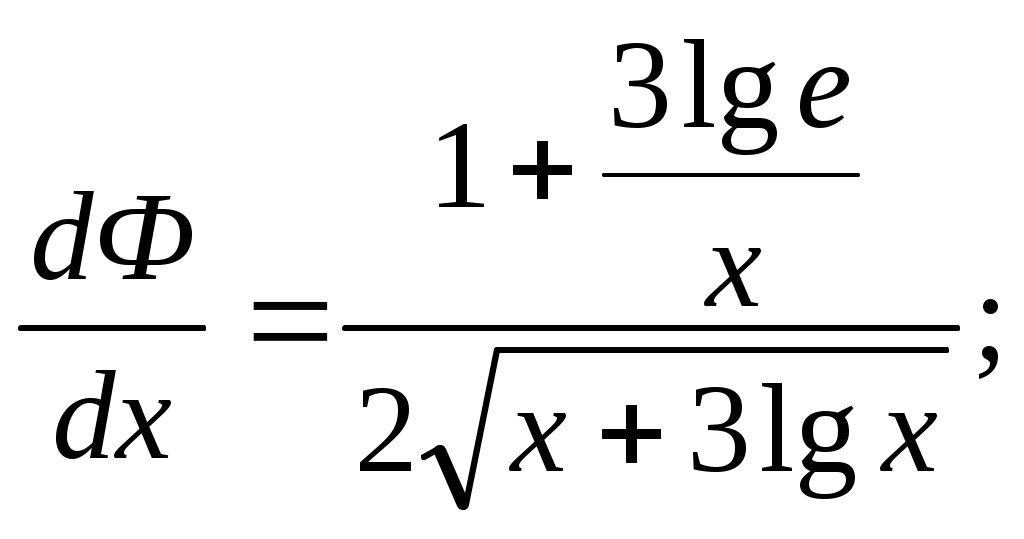 За область изоляции корня можно принять прямоугольник 3 < x < 4; 2 < y < 2,5 Процесс сходится, но так как 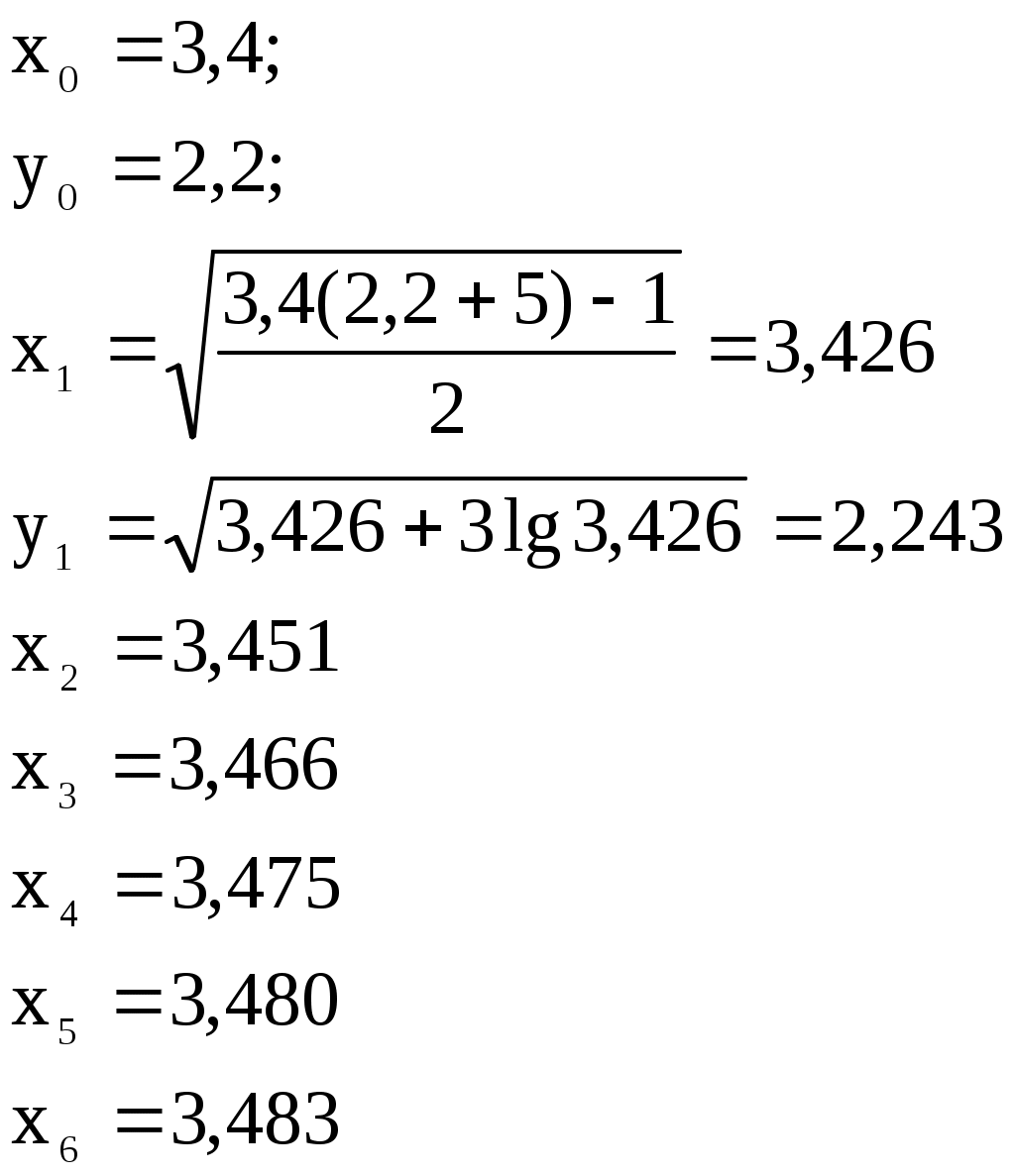 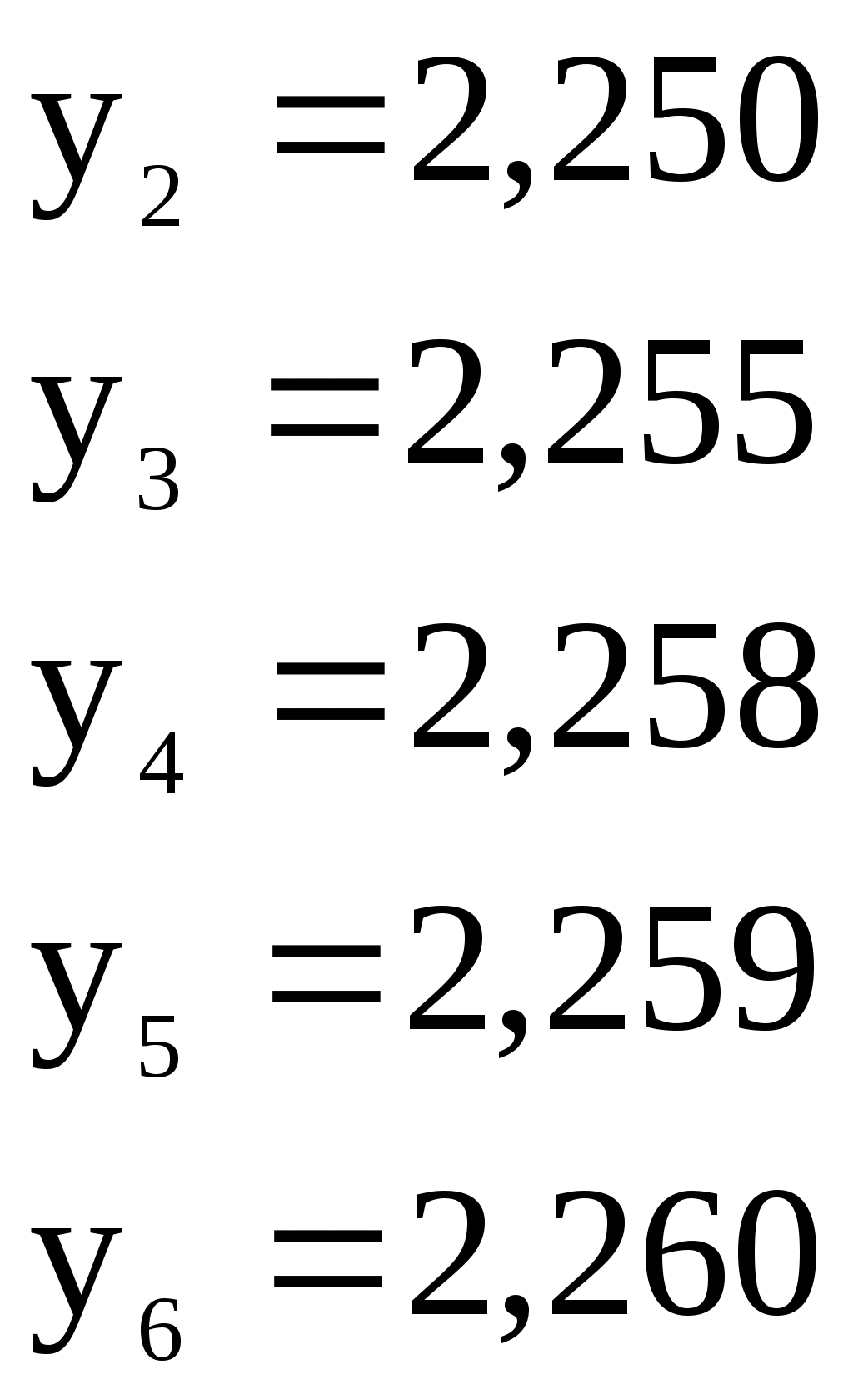 ЗАДАНИЯ (для КР и зачёта) Решить при помощи метода Ньютона–Рафсона системы уравнений, определив точку начального приближения графически: 1) 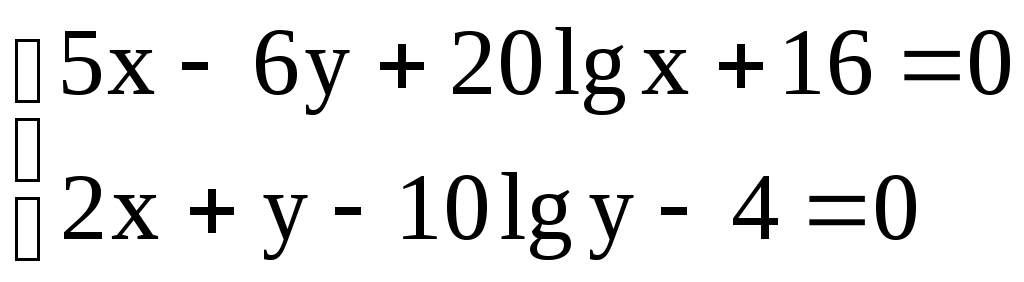 , , 2) 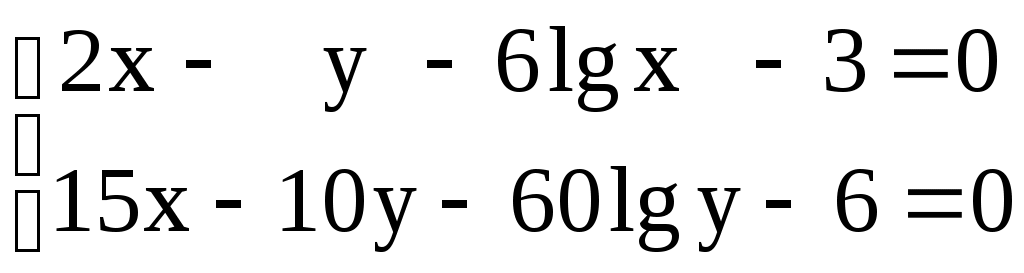 , ,3) 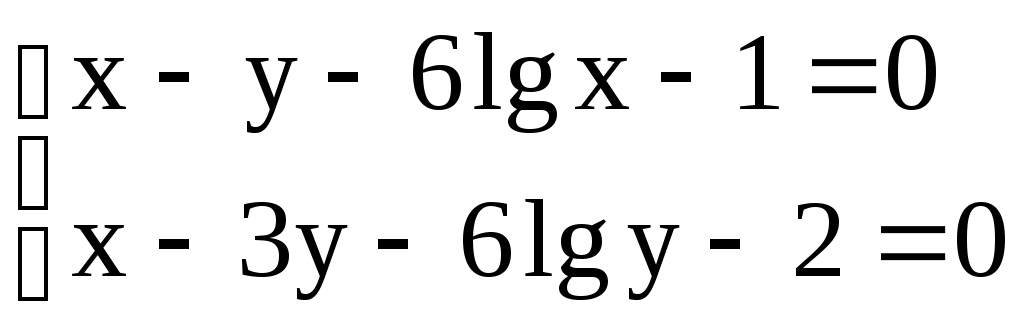 , , 4) 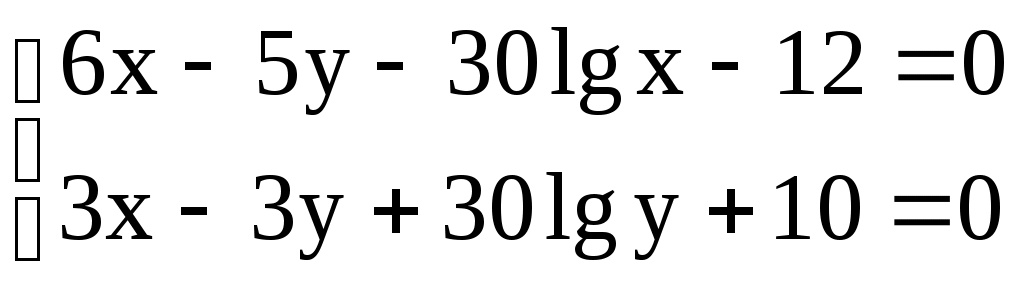 , ,5) 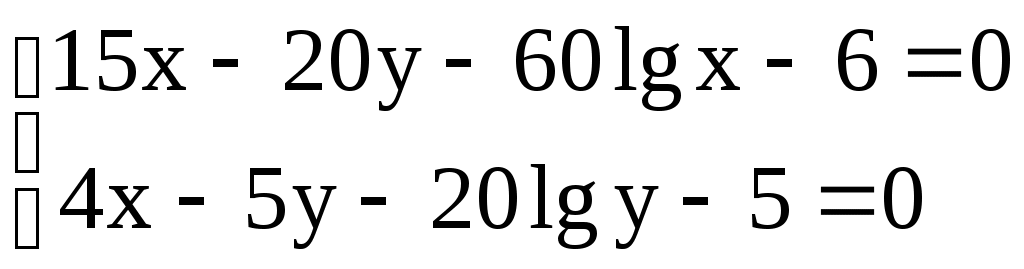 , , 6) 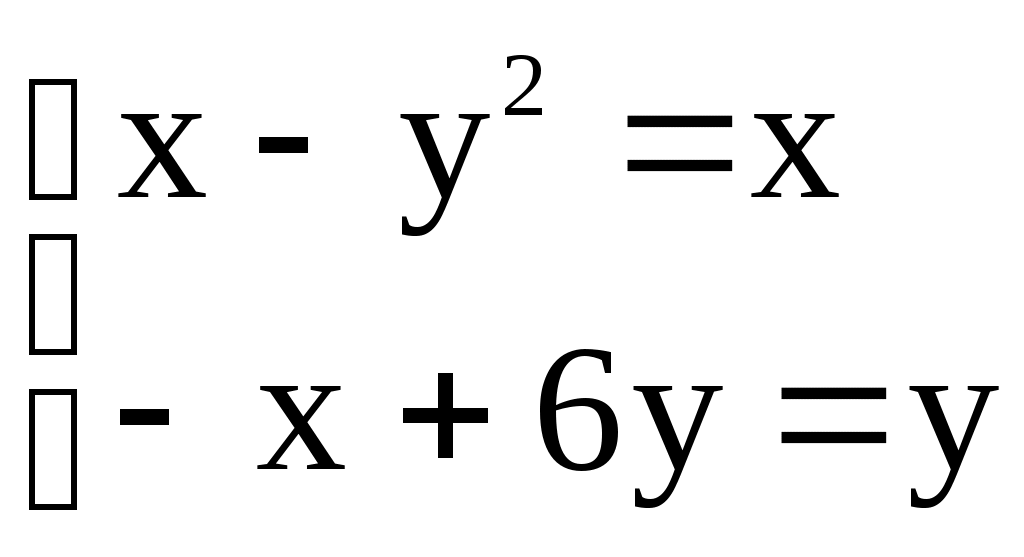 , ,7) 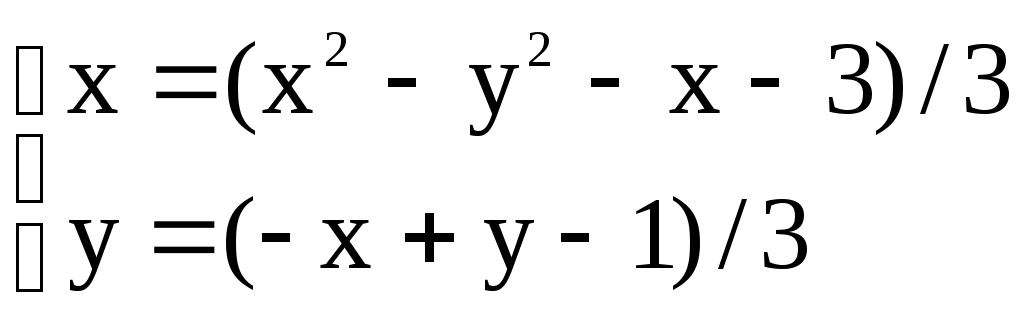 , , 8) 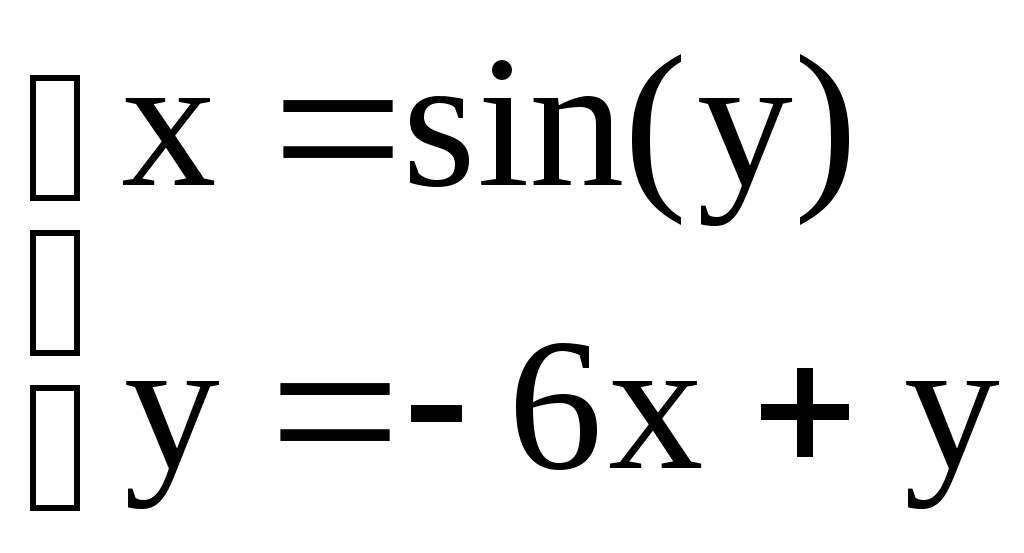 , ,9) 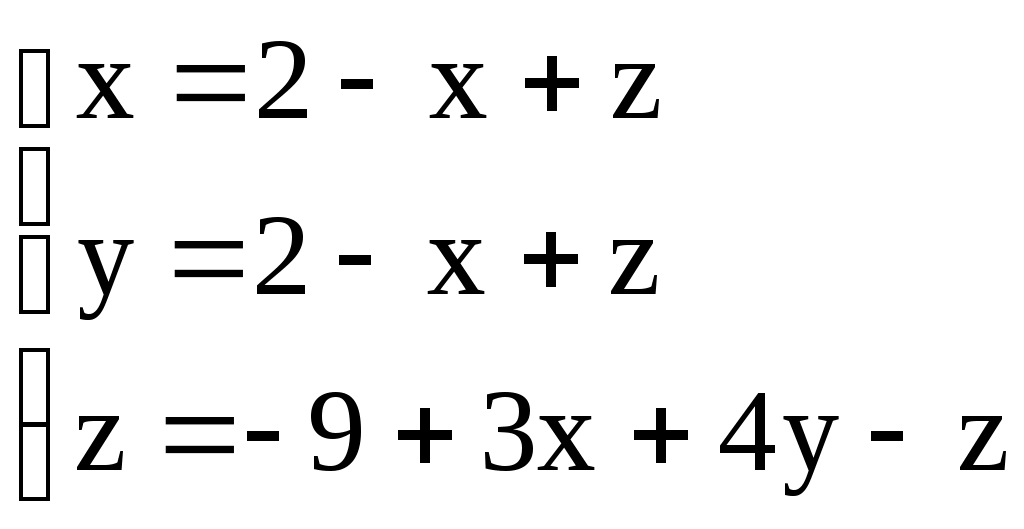 , ,10) 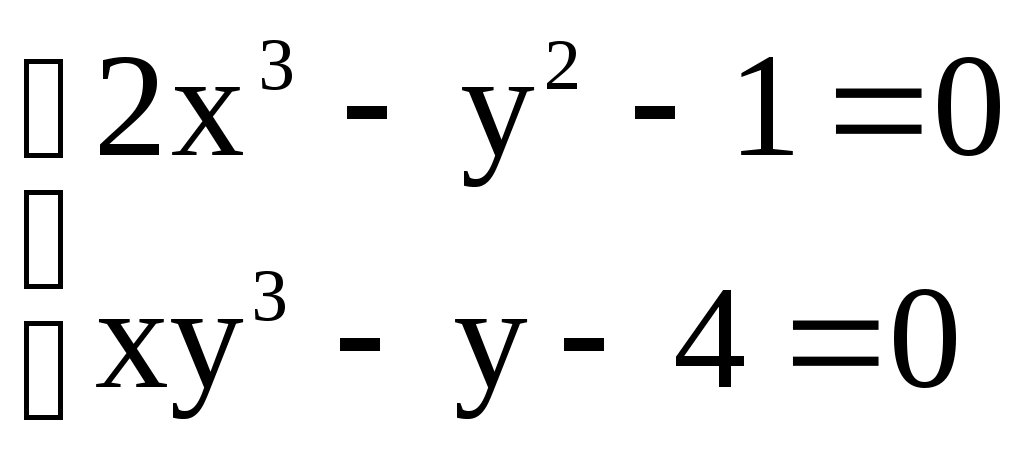 Системы линейных уравнений Метод Простой итерации Пусть дана система n линейных алгебраических уравнений с n неизвестными 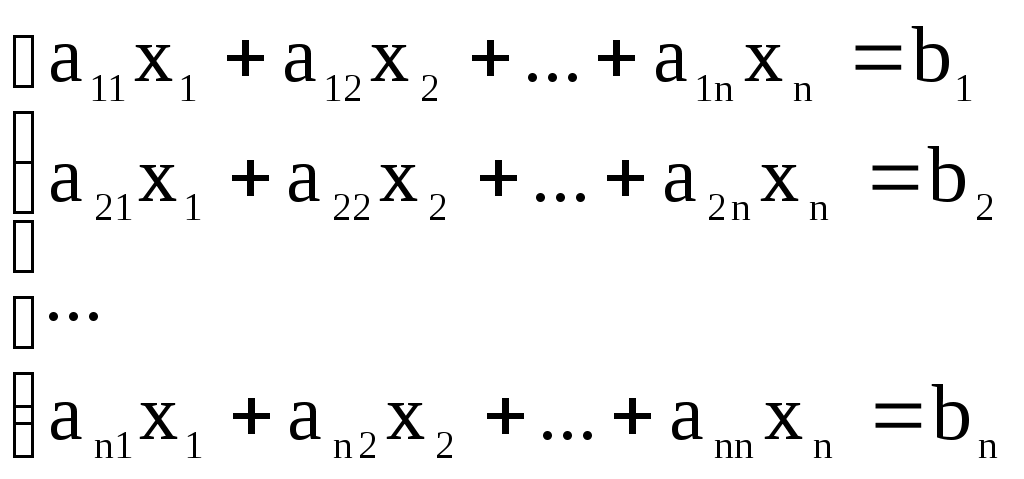 Перепишем систему уравнений в виде: 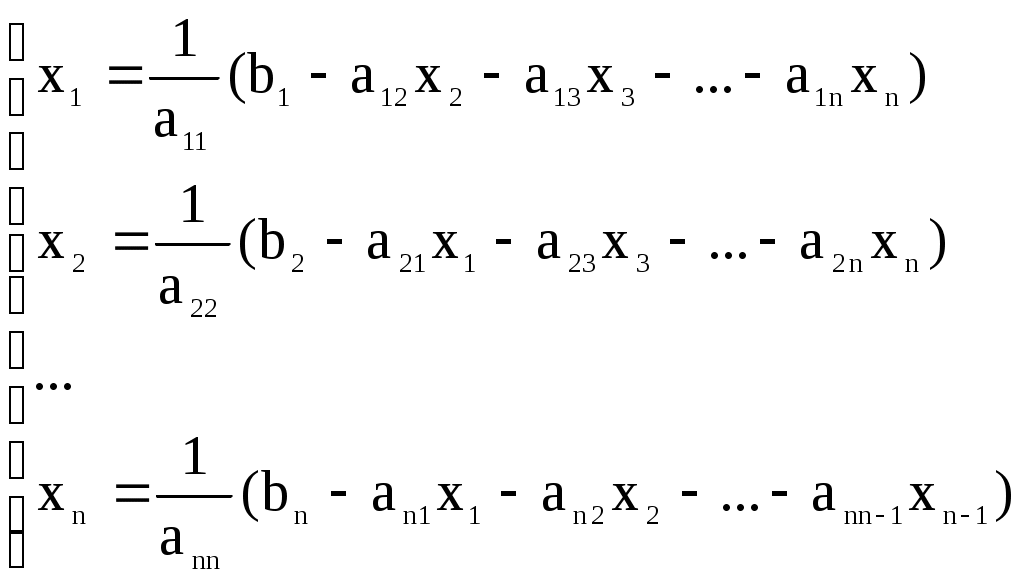 Обозначим правую часть i-го уравнения через 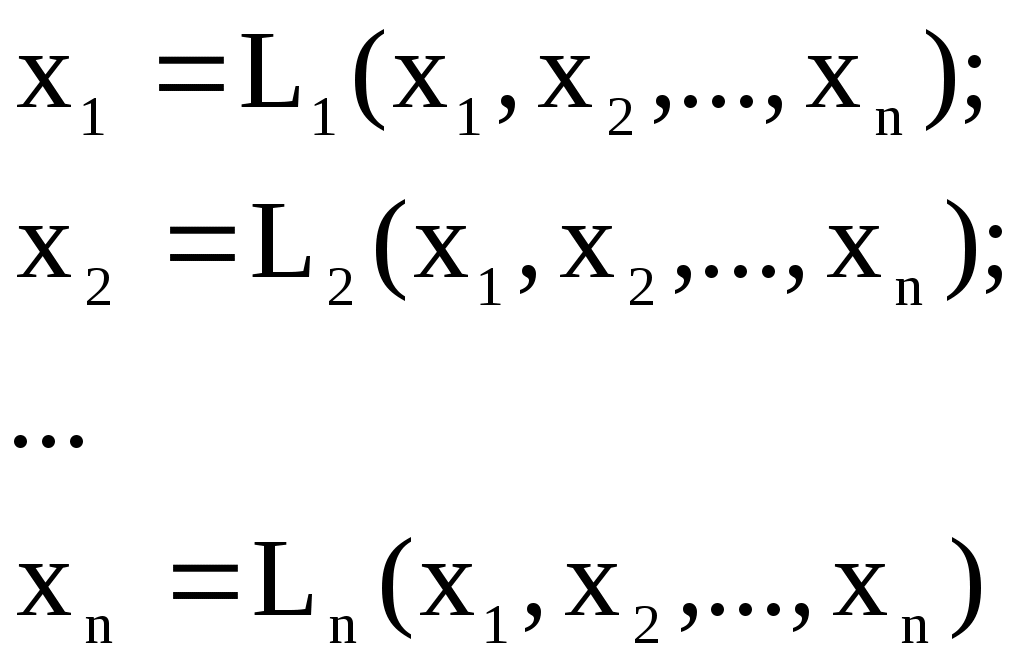 Зададимся начальными приближениями корней системы 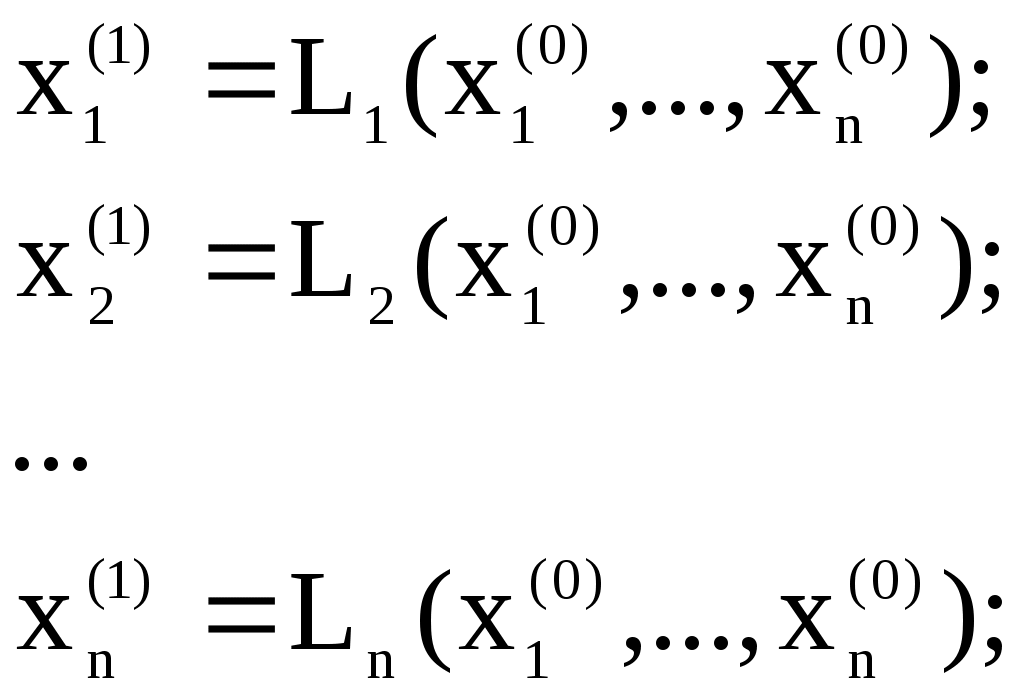 |
