вычеслительная математика. Вычеслительная математика. Почта
 Скачать 1.21 Mb.
|
|
Итерационный процесс продолжается до тех пор, пока все  не станут достаточно близки к  , где i = 1, 2, 3, …, n, то есть: Лучше сравнивать с E относительные разности: 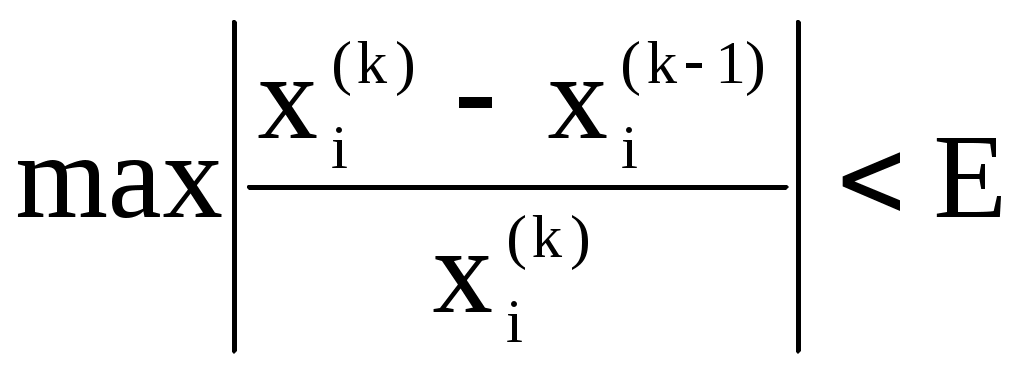 Исследуем сходимость. Пусть  , где xi — истинное значение i-го корня. Так как xi— истинное значение корня, то: Кроме того:  Поэтому:  Иначе:  Обозначим наибольшее из  через  . Тогда  .Если взять:  то  . Так как это справедливо при любых k, то: 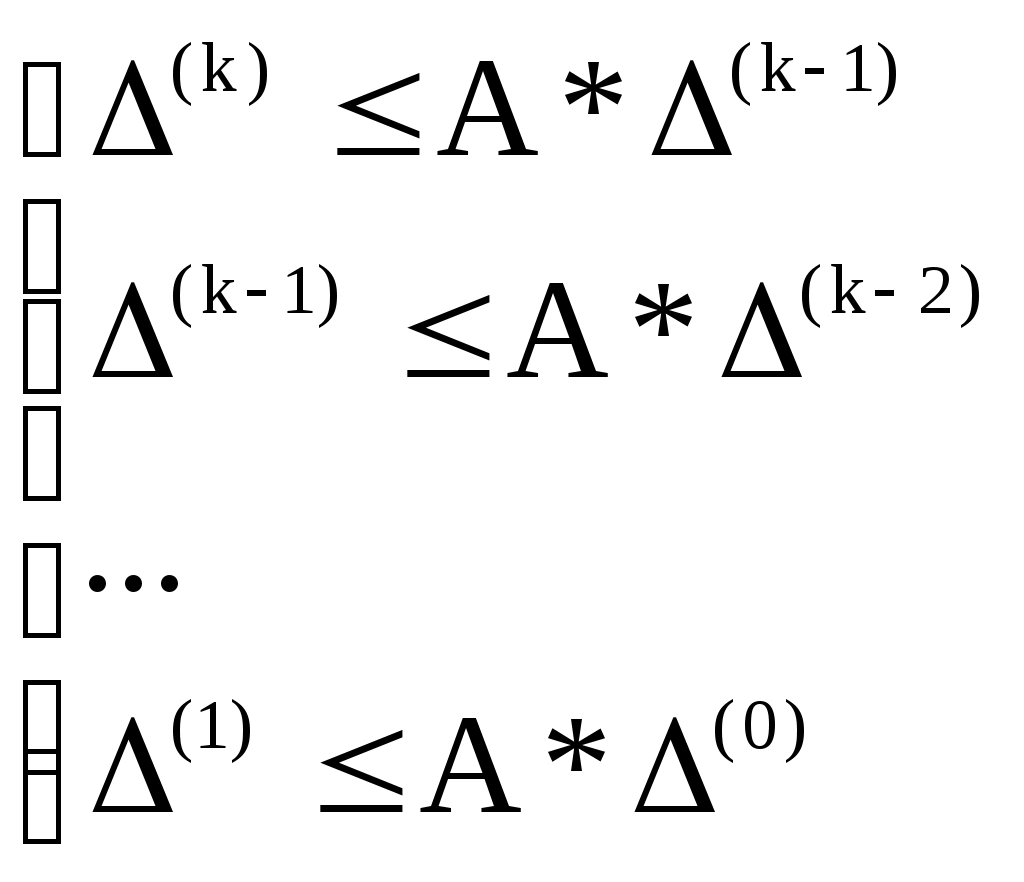 Откуда  . Если A < 1, то  или  при  . Таким образом, условие сходимости  , то есть диагональные элементы системы удовлетворяют условию  . Пример: 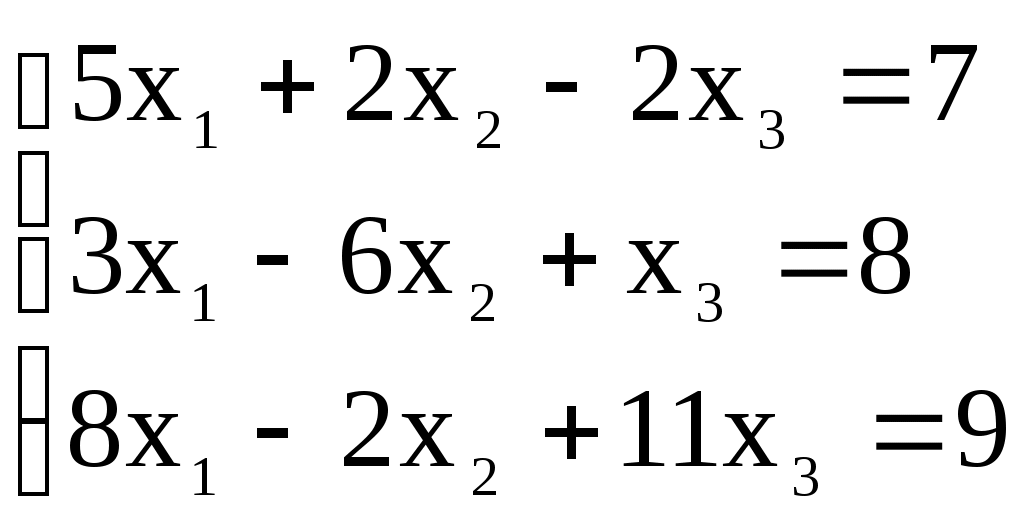 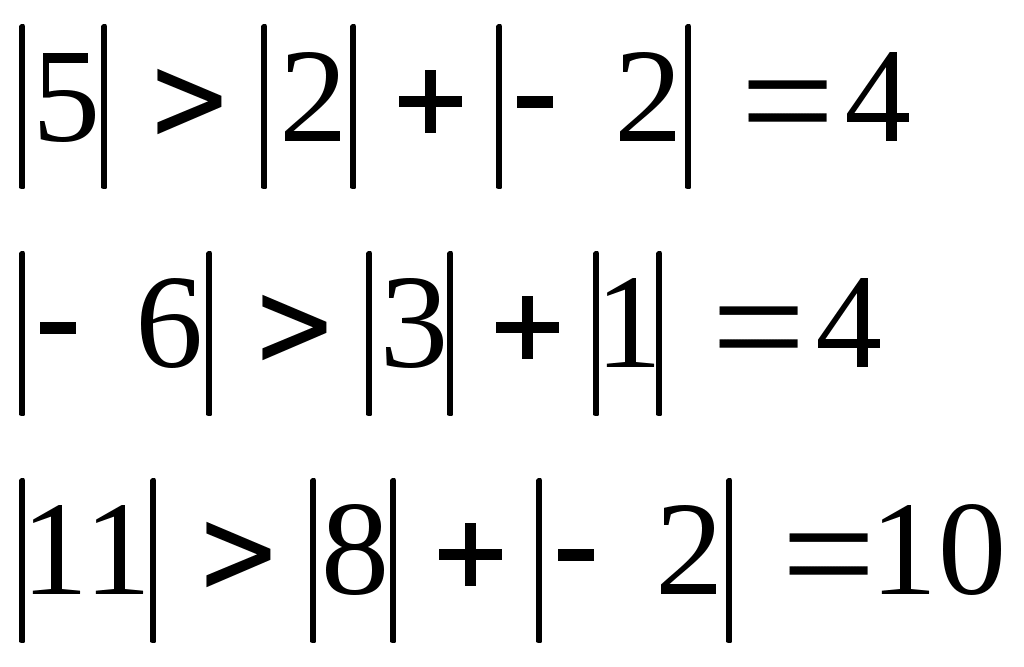 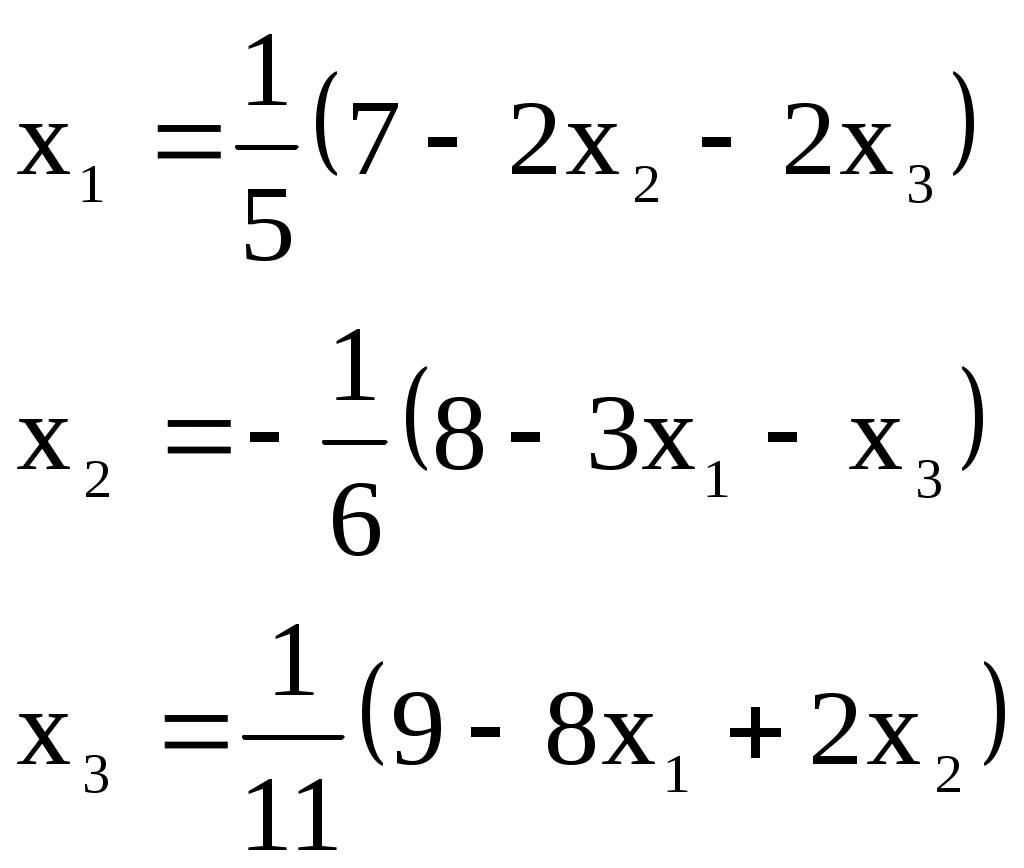 Выбор начальных приближений не влияет на условия сходимости, поэтому чаще всего полагают  .Метод Зейделя Метод Зейделя является модификацией метода простой итерации. Итак дана система уравнений: 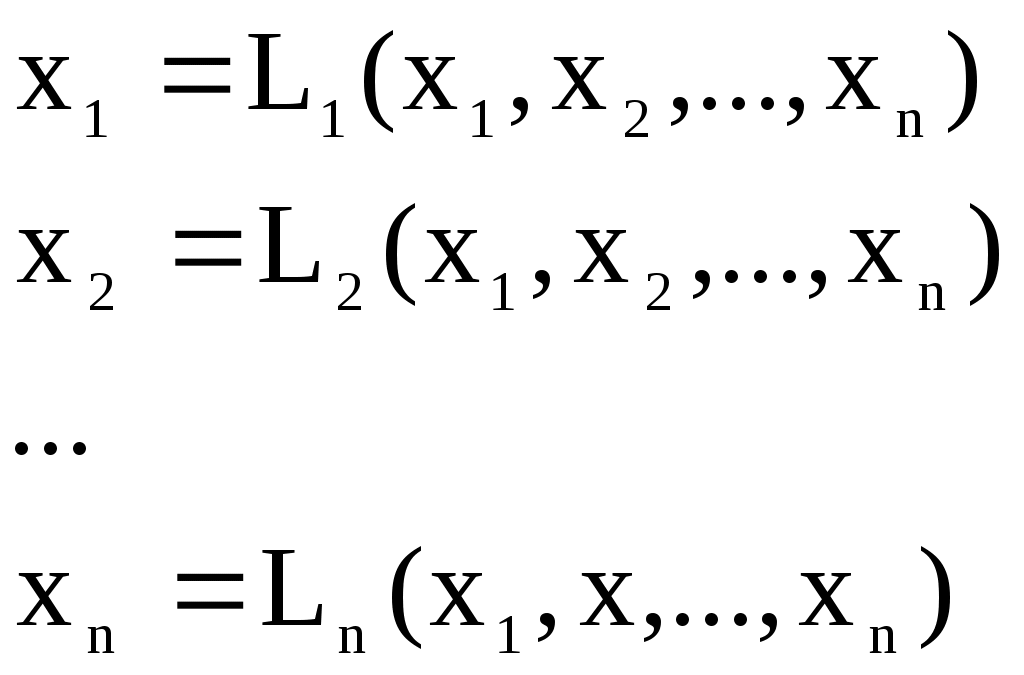 .Для вычисления (k + 1)-го приближения  в методе итераций мы использовали  , где i = 1, 2, …, n, но так как к моменту вычисления  уже найдены  то возникает идея: при нахождении использовать найденные ранее  . В этом и заключается метод Зейделя: для вычисления (k + 1)-го приближения  используется не только k-e, но и (k+1)-e приближения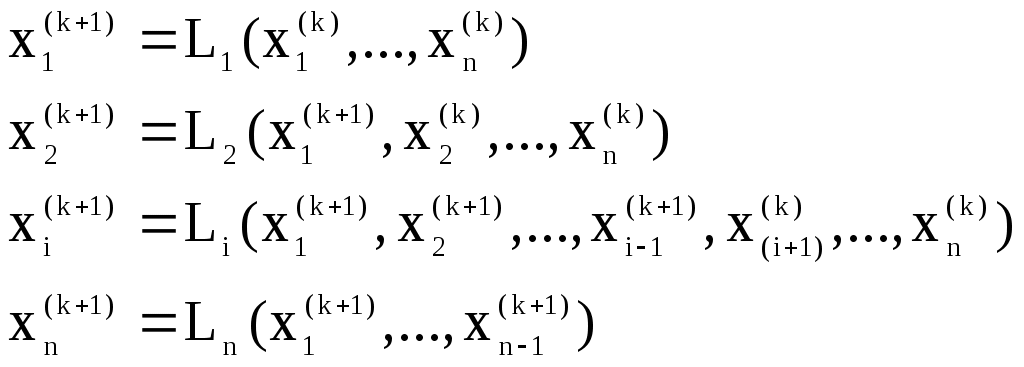: Пример. 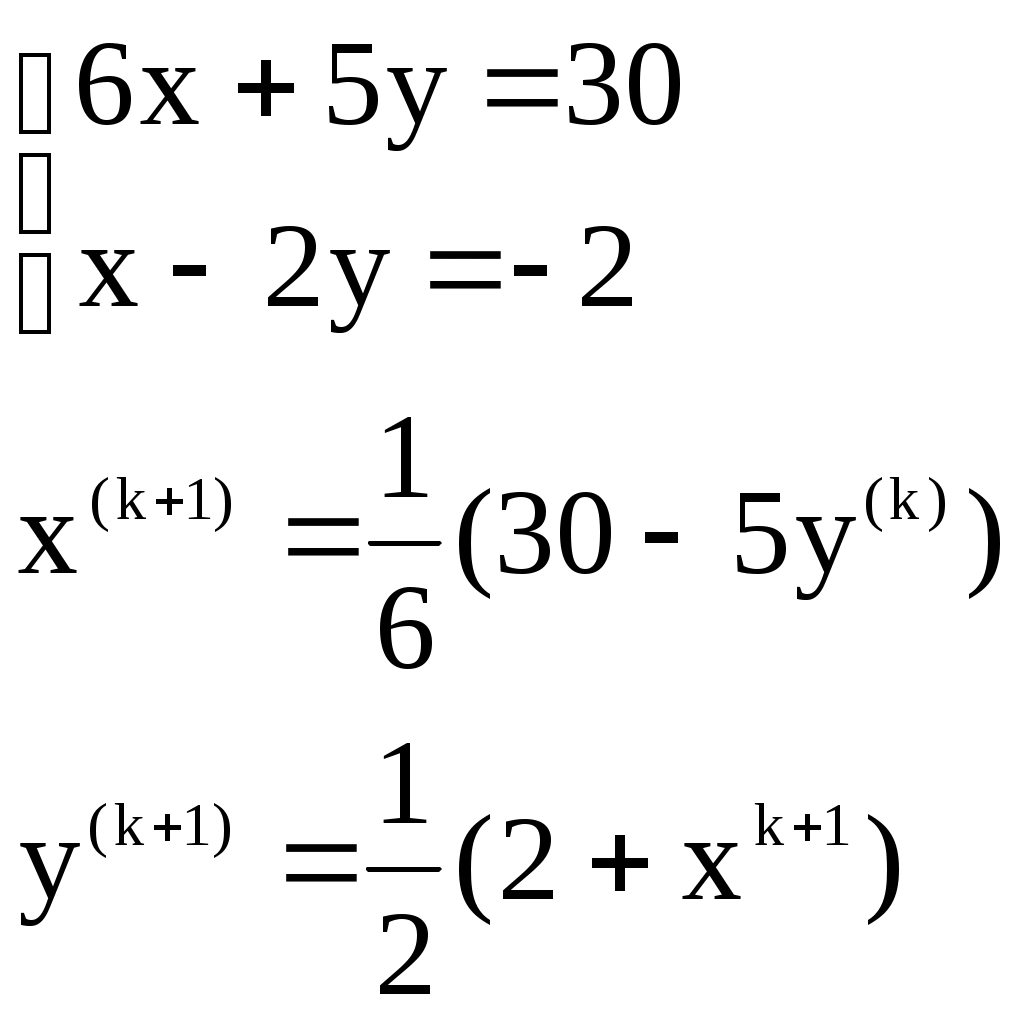 В случае, если коэффициенты решаемой системы не удовлетворяют условию сходимости, то с помощью линейного комбинирования уравнений исходной системы получают новую, для которой сходимость обеспечивается. Для этого выбирают из системы уравнений такие, модули коэффициентов в которых больше суммы модулей остальных коэффициентов. Выбранные уравнения записывают так, чтобы наибольший по модулю коэффициент оказался диагональным. 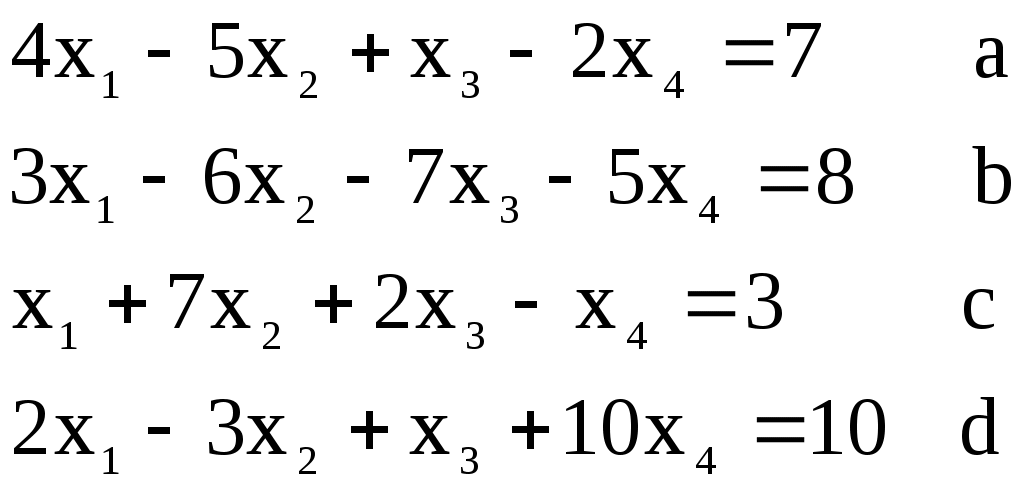 Уравнение с):  - будет 2-е уравнениеУравнение d): 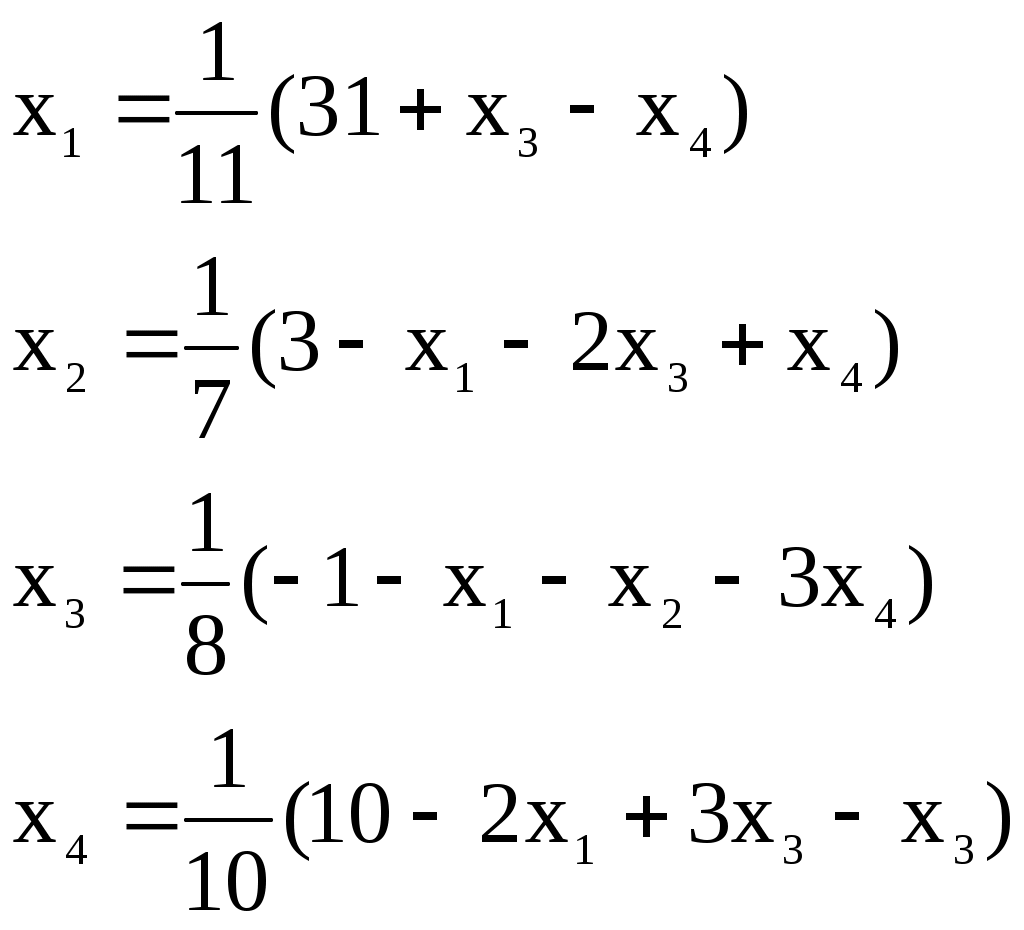 - будет 4-е уравнениеa) - b):  - будет 3-е уравнение,  .a) + b) + 2c) + d):  - 1-е уравнение,   При получении системы уравнений, удовлетворяющей условиям сходимости метода итераций, необходимо, чтобы каждое уравнение исходной системы, не вошедшее в явном виде в новую систему, попало хотя бы в одну из линейных комбинаций. Примеры. Программные реализации некоторых численных методов в среде VBforApplications Sub Метод_Гаусса() Dim m As Integer 'кол-во ур-й СЛАУ или кол-во строк Dim n As Integer 'кол-во столбцов в матрице коэффициентов Dim a(100, 101) As Single 'матрица коэффициентов Dim c(1 To 100) As Single 'матрица для хранения результатов Dim i As Integer 'счетчик цикла Dim l As Integer 'счетчик цикла Dim z As Integer 'счетчик Dim j As Integer 'счетчик цикла Dim d As Integer 'счетчик Dim f As Single 'переменная для хранения эл-ов массива Dim b As Single 'переменная для хранения эл-ов массива Dim x As Single 'вспомогательная переменная Dim p As Integer 'счетчик цикла x = 0 Worksheets(1).Cells(1, 1).Value = "Метод Гаусса" 'выводим пояснения на лист1 Worksheets(1).Cells(2, 1).Value = "Коэффициенты системы" Stop 'останов исп-ся для того, чтобы задать коэффициенты системы m = CInt(InputBox("Введите кол-во ур-й СЛАУ")) 'переменной m присваиваем кол-во ур-й СЛАУ n = m + 1 'коэффициентов будет на 1 больше, чем уравнений СЛАУ Worksheets(1).Cells(m + 3, 1).Value = "Результат:" 'выводим пояснение на лист1 For i = 1 To m 'с листа считываем коэффициенты в массив коэффициентов For j = 1 To n a(i, j) = Worksheets(1).Cells(i + 2, j).Value Next j Next i z = 0 d = 0 1 For i = 1 To (m - z) 'Методом исключения Гаусса преобразуем матрицу коэффициентов СЛАУ b = a(i + z, z + 1) For j = 1 To (n - z) If (d = 0) Then f = a(i + z, j + z) For l = (1 + z) To n a(i + z, l) = a(i + z, l) / f Next l d = d + 1 If z = (m - 1) Then GoTo 3 GoTo 4 Else: a(i + z, j + z) = a(i + z, j + z) - a(z + 1, j + z) * b End If Next j 4 Next i z = z + 1 d = d - 1 GoTo 1 3 For i = m To 1 Step -1 'выведем преобразованную матрицу коэффициентов СЛАУ на лист2 For j = n To 1 Step -1 Worksheets(2).Cells(i, j).Value = a(i, j) Next j Next i c(m) = a(m, n) 'запоминаем найденную переменную в матрицу резудьтата For i = (m - 1) To 1 Step -1 'ищем значения остальных переменных x = a(i, n) For j = (n - 1) To (i + 1) Step -1 x = x - a(i, j) * c(j) Next j 5 c(i) = x 'заносим найденное значение в матрицу результата Next i For i = 1 To m 'выводим корни СЛАУ на лист1 Worksheets(1).Cells(m + 4, i).Value = c(i) Next i End Sub Sub Метод_Простых_итераций() Dim n As Integer 'порядок матрицы системы Dim a(100, 100) As Double 'преобразованная матрица Dim x(100) As Double 'матрица для хранения результатов Dim f(100) As Double 'матрица для хранения результатов Dim b(100) As Double 'столбец свободных членов Dim e As Double 'погрешность Dim i As Integer 'счетчик цикла Dim j As Integer 'счетчик цикла Dim c As Boolean 'Переменная для принятия возвращаемого функцией значения n = CInt(InputBox("Введите порядок матрицы системы")) 'переменной m присваиваем порядок матрицы системы Worksheets(3).Cells(1, 1).Value = "Метод простых итераций" 'выводим пояснения на лист1 Worksheets(3).Cells(2, 1).Value = "Преобразованная матрица" Worksheets(3).Cells(2, n + 2).Value = "Столбец свободных членов" Worksheets(3).Cells(2, n + 6).Value = "Столбец начальных приближений" Worksheets(3).Cells(n + 3, 1).Value = "Результат" Worksheets(3).Cells(n + 3, 3).Value = "Счетчик числа итераций" Stop 'останов исп-ся для того, чтобы задать коэффициенты системы e = CDbl(InputBox("Введите погрешность")) For i = 1 To n 'с листа считываем элементы в матрицу a For j = 1 To n a(i, j) = Worksheets(3).Cells(i + 2, j).Value Next j Next i For j = 1 To n 'с листа считываем элементы в матрицу b b(j) = Worksheets(3).Cells(j + 2, n + 2).Value Next j For j = 1 To n 'с листа считываем элементы(начальные приближения) в матрицу x x(j) = Worksheets(3).Cells(j + 2, n + 6).Value Next j c = Itera(n, a(), b(), x(), f(), e) 'Вызываем ф-ю Itera и возвращаемое значение присваиваем переменной с If (c = False) Then MsgBox ("Условие сходимости не выполняется"): GoTo 1 'Если ф-я вернула False For j = 1 To n 'Выводим решение на лист1 Worksheets(3).Cells(n + 3 + j, 1).Value = x(j) Next j 1 End Sub Function Itera(n As Integer, a() As Double, b() As Double, x() As Double, f() As Double, e As Double) As Boolean Dim i As Integer, j As Integer, p As Integer 'Счетчики цикла Dim s As Double 'Переменная для суммирования элементов уравнения всех, кроме диагонального Dim m As Double 'Переменная для хранения модуля разности между ближайшими приближениями Dim s1 As Double Dim k As Integer ' счетчик числа итерации Dim v As Double 'Переменная для хранения передыдущего приближения k = 0 For i = 1 To n 'Проверяем выполняется ли условие сходимости s = 0 For j = 1 To n If j <> i Then s = s + Abs(a(i, j)) 'Если элемент не диагональный Next j If s >= Abs(a(i, i)) Then Itera = False: GoTo 2 'Если условие сходимости не выполняется Next i Do m = 0 For i = 1 To n 'Просматриваем строки матрицы коэффициентов s1 = 0 For j = 1 To n 'Просматриваем столбцы матрицы коэффициентов s1 = s1 + a(i, j) * x(j) Next j v = x(i) 'Запоминаем приближение f(i) = x(i) - (1 / a(i, i)) * (s1 - b(i)) 'Высчитываем следующее приближение If (Abs(v - f(i)) > m) Then m = Abs(v - f(i)) 'Запоминаем модуль разности ' соседних приближений для сравнения его затем с заданной точностью Next i For p = 1 To n x(p) = f(p) Next p k = p + 1 'Увеличиваем значение счетчика Loop While m >= e 'Продолжаем вычисления пока не достигнута точность Itera = True Worksheets(3).Cells(n + 4, 3).Value = k 'Выводим значение счетчика на лист 2 End Function Sub Метод_Зейделя() Dim n As Integer 'порядок матрицы системы Dim a(100, 100) As Double 'преобразованная матрица Dim x(100) As Double 'матрица для хранения результатов Dim b(100) As Double 'столбец свободных членов Dim e As Double 'погрешность Dim i As Integer 'счетчик цикла Dim j As Integer 'счетчик цикла Dim c As Boolean 'Переменная для принятия возвращаемого функцией значения n = CInt(InputBox("Введите порядок матрицы системы")) 'переменной m присваиваем порядок матрицы системы Worksheets(2).Cells(1, 1).Value = "Метод Зейделя" 'выводим пояснения на лист1 Worksheets(2).Cells(2, 1).Value = "Преобразованная матрица" Worksheets(2).Cells(2, n + 2).Value = "Столбец свободных членов" Worksheets(2).Cells(2, n + 6).Value = "Столбец начальных приближений" Worksheets(2).Cells(n + 3, 1).Value = "Результат" Worksheets(2).Cells(n + 3, 3).Value = "Счетчик числа итераций" Stop 'останов исп-ся для того, чтобы задать коэффициенты системы e = CDbl(InputBox("Введите погрешность")) For i = 1 To n 'с листа считываем элементы в матрицу a For j = 1 To n a(i, j) = Worksheets(2).Cells(i + 2, j).Value Next j Next i For j = 1 To n 'с листа считываем элементы в матрицу b b(j) = Worksheets(2).Cells(j + 2, n + 2).Value Next j For j = 1 To n 'с листа считываем элементы(начальные приближения) в матрицу x x(j) = Worksheets(2).Cells(j + 2, n + 6).Value Next j c = Zeidel(n, a(), b(), x(), e) 'Вызываем ф-ю Zeidel и возвращаемое значение присваиваем переменной с If (c = False) Then MsgBox ("Условие сходимости не выполняется"): GoTo 1 'Если ф-я вернула False For j = 1 To n 'Выводим решение на лист1 Worksheets(2).Cells(n + 3 + j, 1).Value = x(j) Next j 1 End Sub Function Zeidel(n As Integer, a() As Double, b() As Double, x() As Double, e As Double) As Boolean Dim i As Integer, j As Integer 'Счетчики цикла Dim s As Double 'Переменная для суммирования элементов уравнения всех, кроме диагонального Dim m As Double 'Переменная для хранения модуля разности между ближайшими приближениями Dim s1 As Double Dim p As Integer ' счетчик числа итерации Dim v As Double 'Переменная для хранения предыдущего приближения p = 0 For i = 1 To n 'Проверяем выполняется ли условие сходимости s = 0 For j = 1 To n If j <> i Then s = s + Abs(a(i, j)) 'Если элемент не диагональный Next j If s >= Abs(a(i, i)) Then Zeidel = False: GoTo 2 'Если условие сходимости не выполняется Next i Do m = 0 For i = 1 To n 'Просматриваем строки матрицы коэффициентов s1 = 0 For j = 1 To n 'Просматриваем столбцы матрицы коэффициентов s1 = s1 + a(i, j) * x(j) Next j v = x(i) 'Запоминаем приближение x(i) = x(i) - (1 / a(i, i)) * (s1 - b(i)) 'Высчитываем следующее приближение If (Abs(v - x(i)) > m) Then m = Abs(v - x(i)) 'Запоминаем модуль разности ' соседних приближений для сравнения его затем с заданной точностью Next i p = p + 1 'увеличиваем счетчик Loop While m >= e 'Продолжаем вычисления пока не достигнута точность Zeidel = True Worksheets(2).Cells(n + 4, 3).Value = p 'Выводим значение счетчика на лист 2 End Function ЗАДАНИЯ (для КР и зачёта) Методом Зейделя решить с точностью 0,001 систему линейных уравнений, приведя ее к виду, удобному для итераций. Программу реализовать в среде VBA MS Excel. Вариант №1 Вариант №2 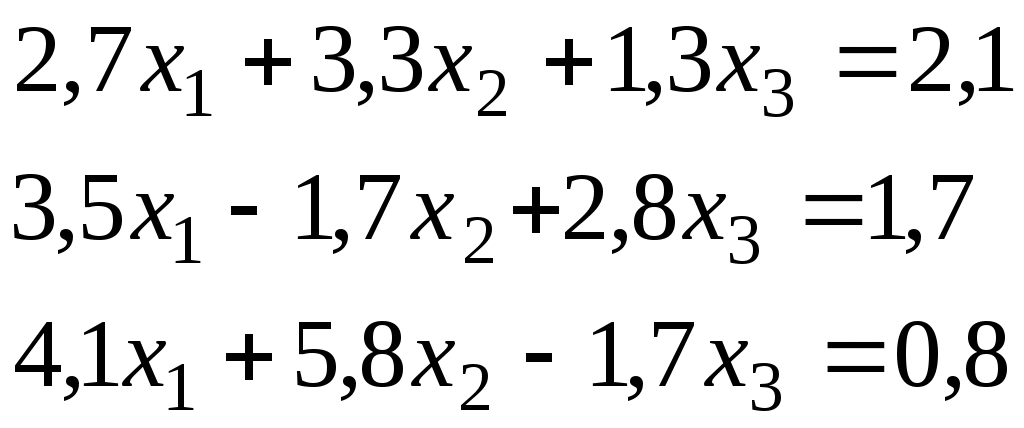 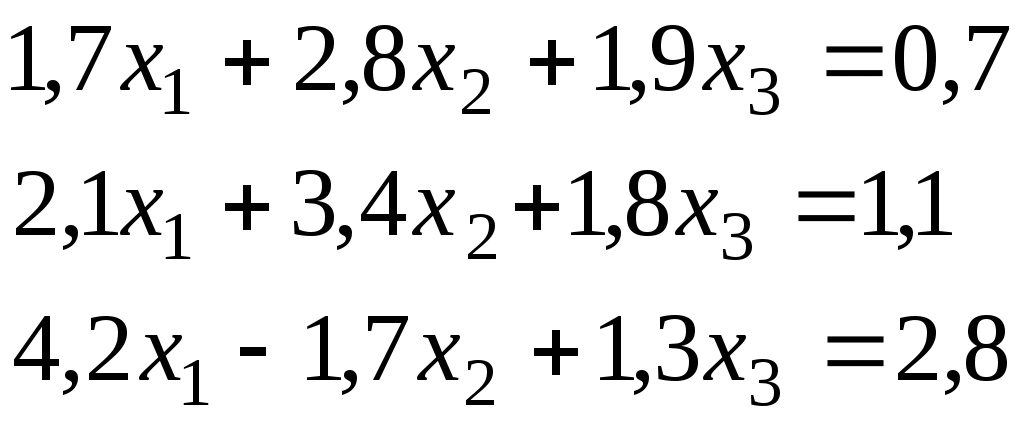 Вариант №3 Вариант №4 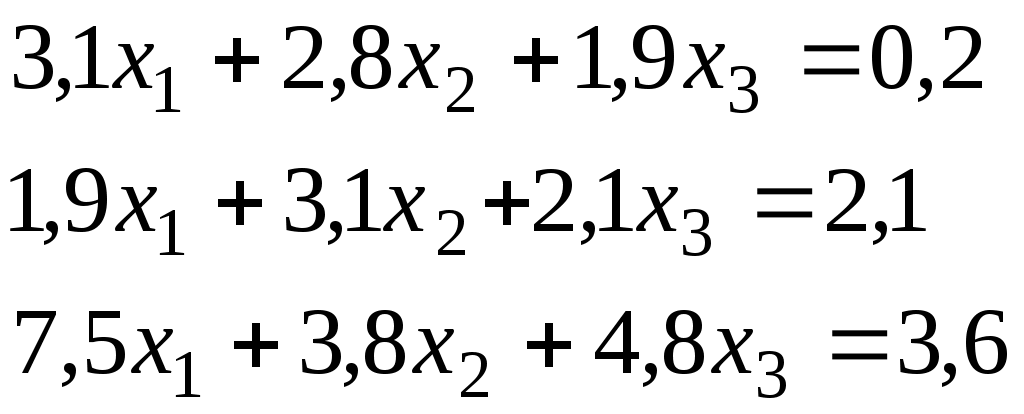 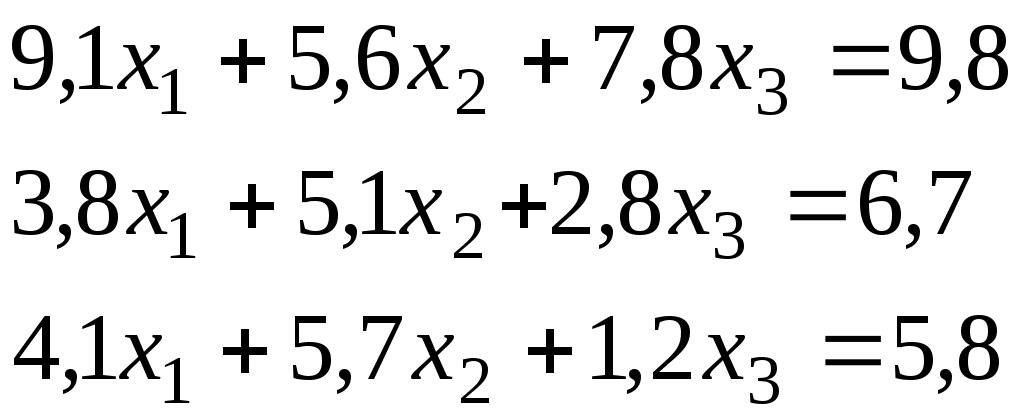 Вариант №5 Вариант №6 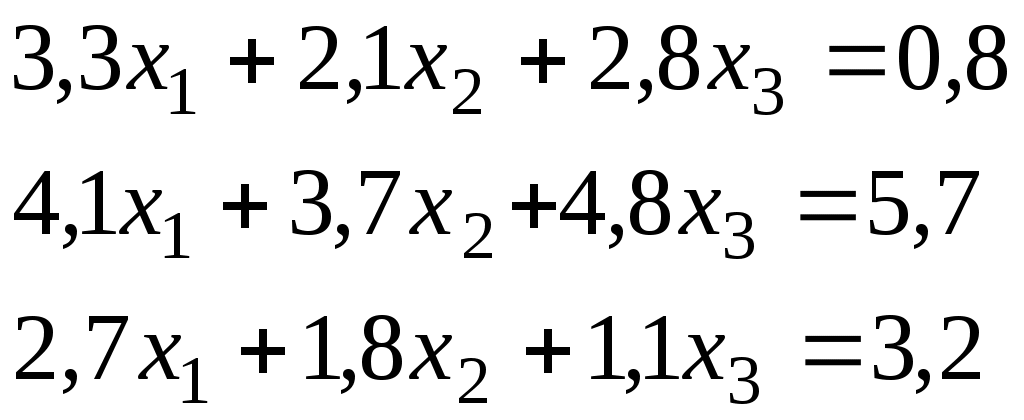 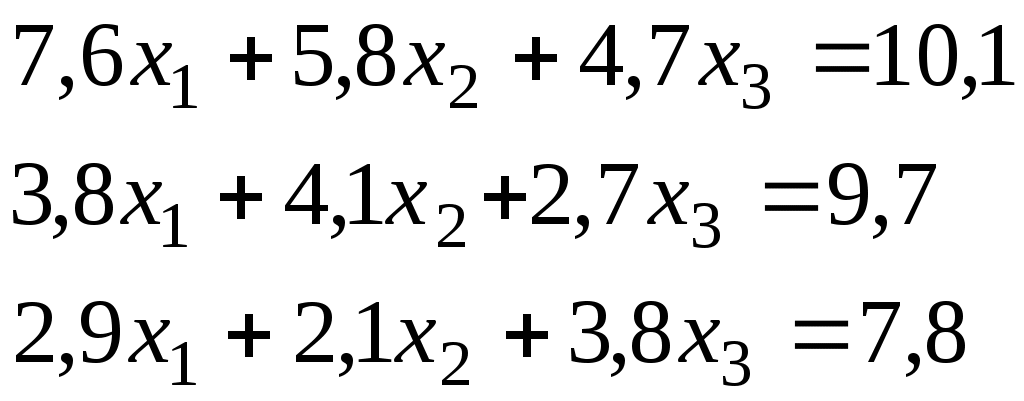 Вариант №7 Вариант №8 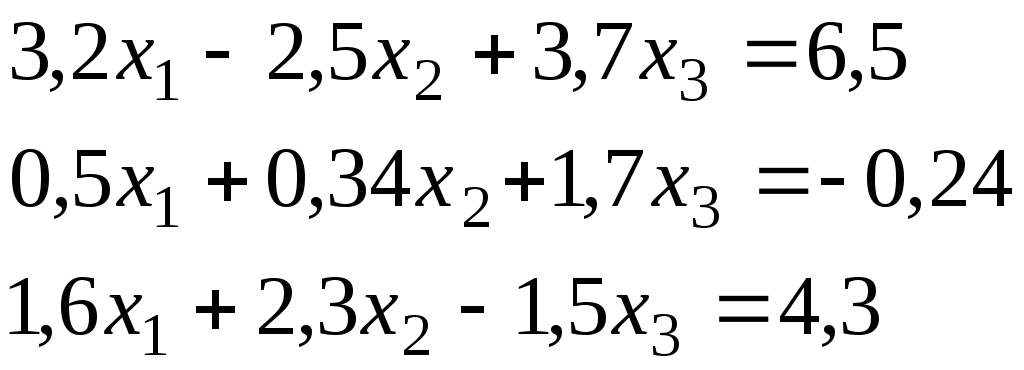 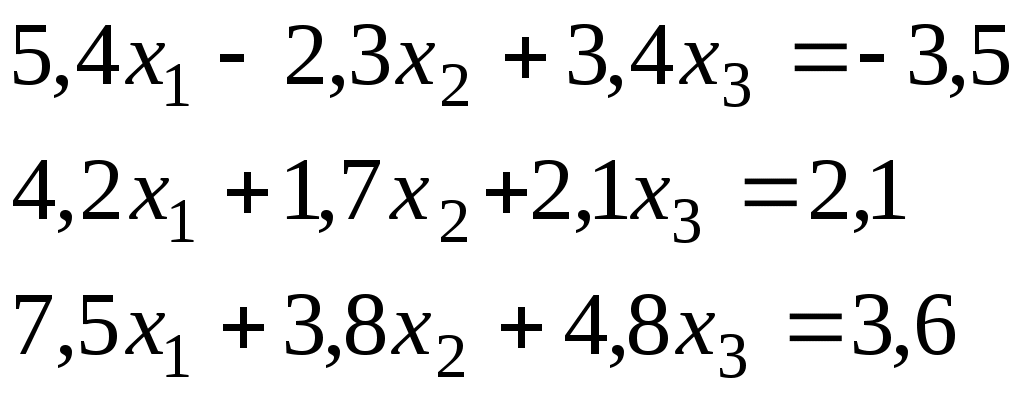 Вариант №9 Вариант №10 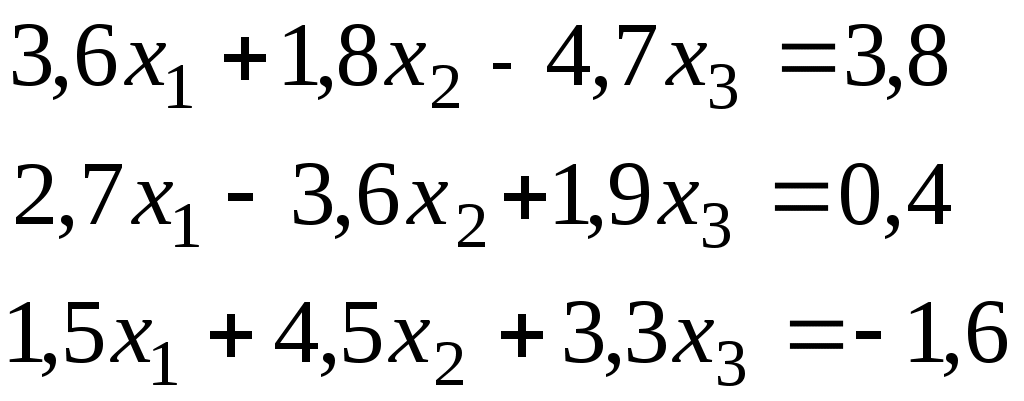 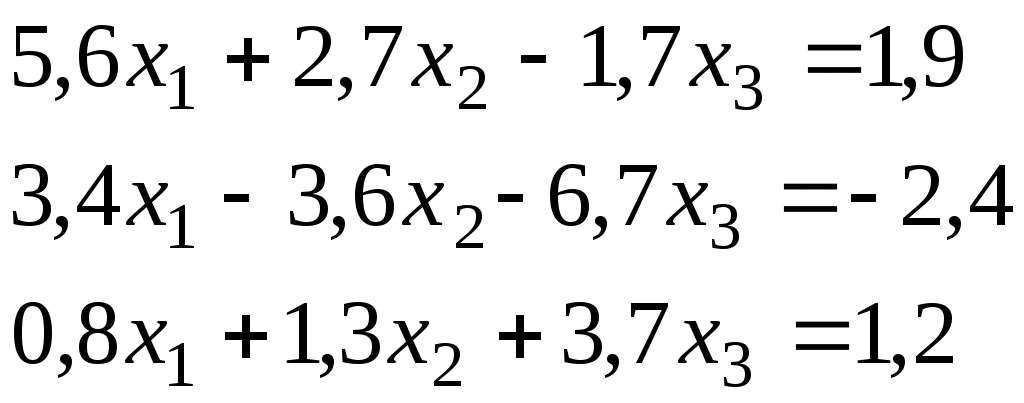 Вариант №11 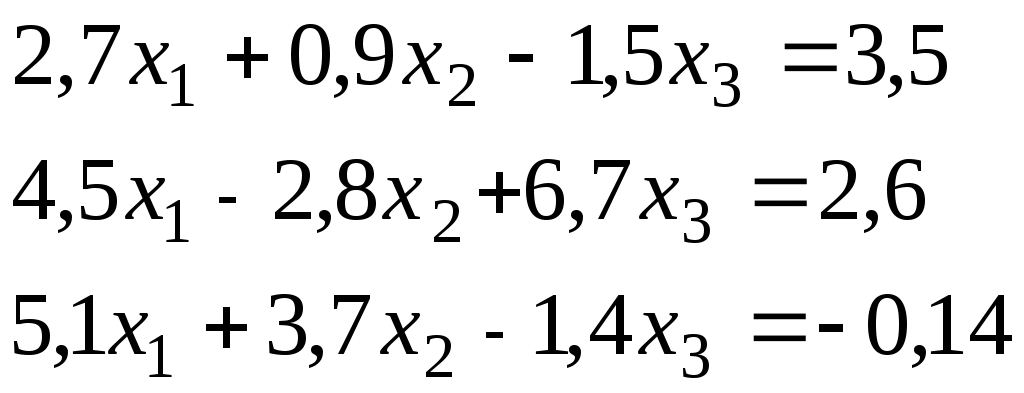 |