ГЛАВА 7. Полевые транзисторы

• Название: Полевые транзисторы
• Дата: 28.02.2018
• Размер: 0.73 Mb.
• Имя файла: ГЛАВА 7.doc
• Тип: Документы; #37396
• страница: 1 из 6

ГЛАВА 7

ПОЛЕВЫЕ ТРАНЗИСТОРЫ

7.1. Общие сведения

Полевые транзисторы – это полупроводниковые приборы, уп­равление током в которых осуществляется изменением проводи­мости токопроводящего канала при воздействии электрического поля, поперечного к направлению тока. Ток в канале создается в результате дрейфового движения основных носителей заряда ка­нала, вызванного продольным электрическим полем. Электрод, от которого носители уходят в канал, называется истоком, а элект­род, принимающий носители в конце канала, – стоком. Исток, ка­нал и сток имеют одинаковый тип электропроводности (n или р). Уп­равляющее поперечное поле создается с помощью электрода, на­зываемого затвором.

Различают полевые транзисторы (ПТ) с изолированным за­твором и затвором на основе электрического перехода (управля­ющим переходом). В качестве управляющего перехода использу­ется р-n-переход и контакт металл-полупроводник (барьер Шотки). В первом случае металлический затвор изолирован от канала тонким слоем диэлектрика, и поэтому полевые транзисторы с изо­лированным затвором сокращенно называют МДП-транзисторами (М – металл, Д – диэлектрик, П – полупроводник). МДП-транзисторы подразделяются на транзисторы со встроенным каналом и с индуцированным каналом. В первом проводящий канал создан технологически («встроен») путем введения соответствующей примеси (донорной для получения n-канала или акцепторной для получения р-канала). Во втором канал возникает (индуцируется) только при подаче на изолированный затвор напряжения опреде­ленной полярности и величины.

В МДП-транзисторе со встроенным каналом и в транзисторе с управляющим переходом при нулевом напряжении на затворе су­ществует канал и в нем протекает начальный ток, если между сто­ком и истоком приложено напряжение. Эти разновидности транзи­сторов принято называть МДП-транзисторами обедненного типа, так как управление током будет заключаться в уменьшении тока (обеднении канала). МДП-транзисторы с индуцированным каналом называют транзисторами обогащенного типа, так как канал в нем появляется при подаче напряжения на затвор. Названия разновид­ностей полевых транзисторов и условные графические обозначе­ния их на схемах приведены в табл. 7.1 (в скобках указаны приня­тые в книге сокращенные названия электродов: И – исток, 3 – за­твор, С – сток, П – подложка). Направление стрелки около подлож­ки указывает на тип канала.

7.2. Полевой транзистор с управляющим р-n-переходом

7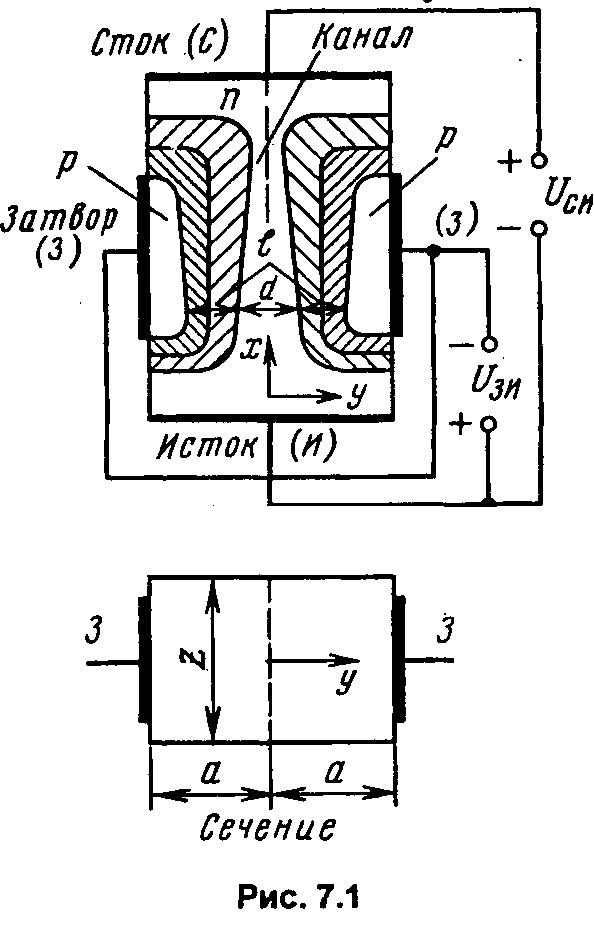.2.1. Устройство и принцип действия

На рис. 7.1 схематично показано устройство двухзатворного ПТ с управляющим р-n-переходом и каналом n-типа. На полупроводни­ковом образце n-типа с двух боковых сторон созданы р-области, так что образуются два электронно-дырочных перехода (обедненные области). Границы переходов создают канал n-типа, выводы с концов которого являются истоком и стоком. Каждая область р-типа яв­ляется затвором. Будем считать сечение образца прямоугольным (ширина Z, толщина 2а), а длину его равной L. Два затвора, распо­ложенные на противоположных гранях образца, для наглядности соединены.

На р-n-переходы подается обратное напряжение, чтобы ток в цепи затвора, а следова­тельно, и необходимая для управления ПТ мощность были ма­лыми. На рис. 7.1 приведена наиболее распространенная схема включения с общим истоком (ОИ).

Положительная разность по­тенциалов между стоком и истоком (U_си > 0) обеспечивает дрей­фовое движение электронов в канале от истока к стоку, т.е. полу­чение тока во внешней цепи, называемого током стока I_с. При изменении обратного напряжения U_зи происходит изменение толщины обедненных слоев р-n-переходов и, следовательно, площади сечения канала и тока I_с.

Профиль канала в состоя­нии равновесия U_си = 0, U_зи = 0) показан на рис. 7.2,а. Увеличи­вая абсолютную величину U_зи. можно добиться совмещения гра­ниц слоев (рис. 7.2,б). Требуемое для этого напряжение называют напряжением отсечки (U_{зи отc}). Значение U_{зи отс} легко найти, используя формулу (3.21) для толщины резкого р-n-перехода, счи­тая напряжение между стоком и истоком равным нулю (U_си = 0):

(7.1)

где N_Д, N_а – концентрации доноров и акцепторов; φ_к – контактная разность потенциалов; q– заряд электрона; ε, ε_о– диэлектричес­кая проницаемость вакуума и относительная диэлектрическая проницаемость.

Напряжение U_зи < 0, но для удобства записи в формуле (7.1) мы далее будем опускать модульные скобки, считая, что U_зи есть абсо­лютная величина обратного напряжения.

Чтобы обедненная область каждого перехода располагалась в основном в n-области и эффективно влияла на сечение канала, необходимо р-n-структуры делать несимметричными (N_Д << N_а). В этом случае вместо (7.1) можно написать:

(7.2)

Для нахождения абсолютного значения напряжения отсечки не­обходимо в (7.2) положить l= а (см. рис. 7.1). Тогда

(7.3)

где

(7.4)

Если можно пренебречь значением контактной разности потенциа­лов, то

(7.5)

Так как мы полагали U_си = 0, то это означает, что толщина обед­ненной области определяется только напряжением на затворе U_зи и остается неизменной во всех сечениях подлине канала (от истока к стоку). Следовательно, остается постоянной и площадь сечения ка­нала S = d·Z. Однако в рабочем режиме ПТ, когда U_си ≠ 0, существу­ет распределение потенциала по координате х вдоль канала. Будем приблизительно считать, что в начале канала у истока (при х = 0) U(0) = 0, а в конце у стока (х = L)U(L) = U_си. Напряжение на р-n-переходе в произвольном сечении складывается из напряжения на за­творе U_зи и U(x). Очевидно, что U(x) увеличивает обратное напря­жение на р-n-переходе. Поэтому для абсолютных значений напря­жения можно написать:

(7.6)

Таким образом, модуль обратного напряжения на переходе при уве­личении х растет, а толщина перехода l соответственно увеличива­ется; толщина канала d и площадь сечения канала S = d·Zуменьша­ются, как показано на рис. 7.1 и 7.2,в.

Для последующего анализа используется так называемое прибли­жение плавного канала, суть которого заключается в том, что толщина обедненной области под затвором считается медленно изменяющей­ся функцией координаты. Другими словами, предполагается, что по­тенциал U(x) вдоль канала изменяется достаточно медленно и в каж­дой точке толщина обедненного слоя может быть найдена по формуле (7.2), если в нее вместо модуля U_зиподставить U_p-n(x) из (7.6). Тогда

(7.7)

Соответственно толщина канала в любом его сечении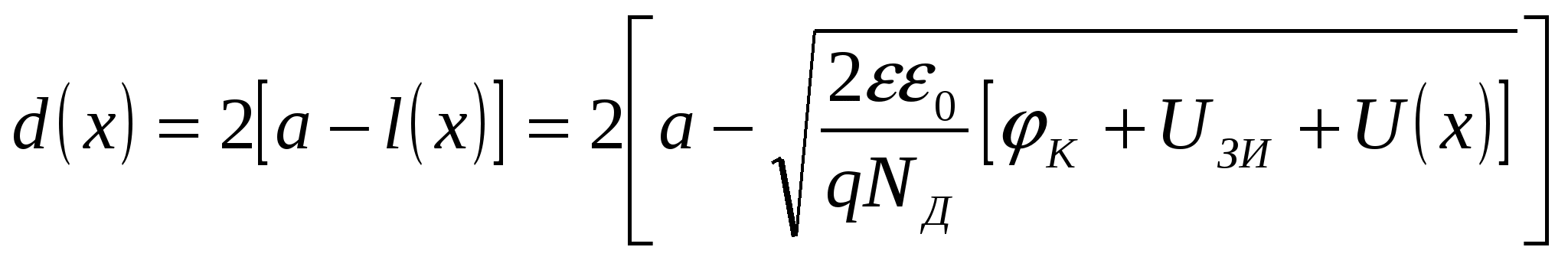

(7.8)

Сумма под корнем – это высота потенциального барьера в произ­вольном сечении. При х = LU(L) = U_си, а толщина канала из (7.7)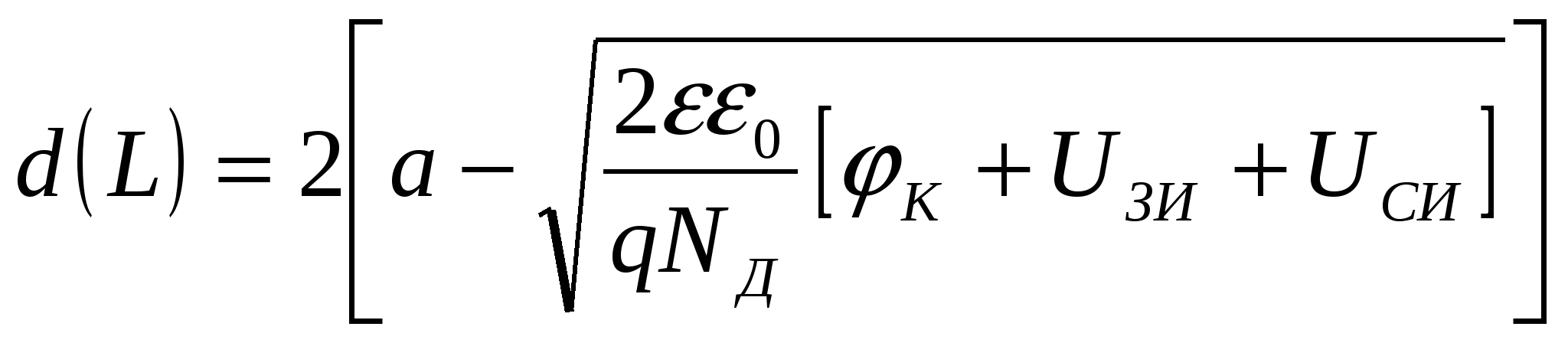

(7.9)

Очевидно, что d(L) = 0 при

(7.10)

Значение U_си в (7.10), соответствующее перекрытию канала около стока (см. рис. 7.2, в) при выбранном значении U_зи, принято назы­вать напряжением насыщения:

(7.11)

В частном случае, когда U_зи = 0 (рис. 7.2,г),

(7.12)

Легко видеть, сравнивая (7.12) и (7.3), что

(7.13)

Напомним, что U_{зи отс} определялось при U_си = 0 как напряжение, при котором происходило смыкание канала по всей его длине (отсечка всего канала, как на рис. 7.2,б). Результат (7.13) очевиден, так как на­пряжение U_зи, необходимое для смыкания канала при U_си = 0, долж­но быть таким же для данного размера а, как и напряжение U_си при U_зи = 0. Различие состоит лишь в том, что в первом случае смыкание происходит по всей длине канала, а во втором – около стока, как пока­зано на рис. 7.2,г. Отсутствие канала при U_{зи отс} означает, что в кана­ле не протекает ток. Будет ли ток во втором случае, мы обсудим поз­же, после того, как выведем формулу для тока в канале (тока стока).

Плотность тока в любом сечении канала определяется законом Ома в дифференциальной форме:

(7.14)

где σ – удельная проводимость; Ex = –dU(x)/dx– продольная напря­женность поля.

Для n-канала при подвижности электронов μ_n и объемной кон­центрации n ≈ N_Д

(7.15)

Ток в канале (ток стока) не зависит от координаты, хотя плотность тока и площадь сечения могут от нее зависеть:

(7.16)

где S(x) = Zd(x) – площадь сечения канала.

Используя (7.16) и (7.14), получаем

(7.17)

Используя (7.8), приведем (7.17) к дифференциальному уравнению вида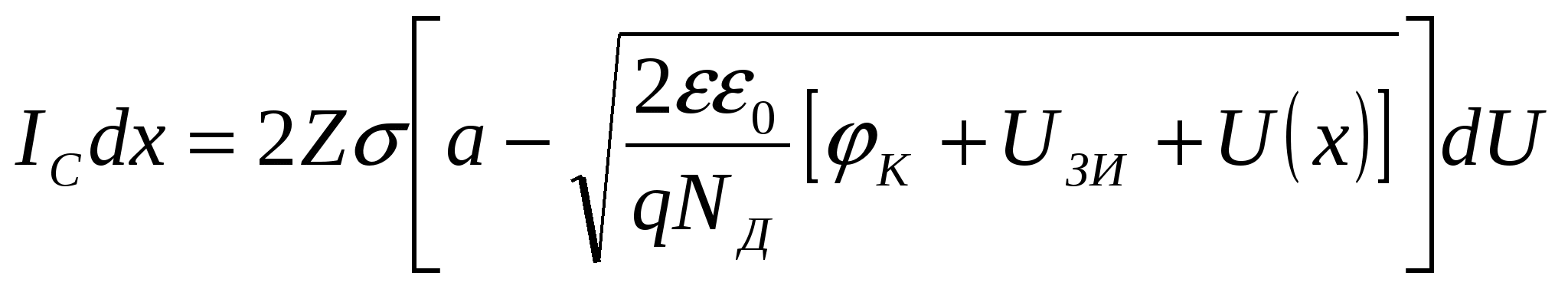

(7.18)

Считая I_с = const, проведем интегрирование от х = 0, когда U(0) = 0, до х=L, когда U(L) = U_си. Опуская промежуточные операции, запи­шем окончательно решение в виде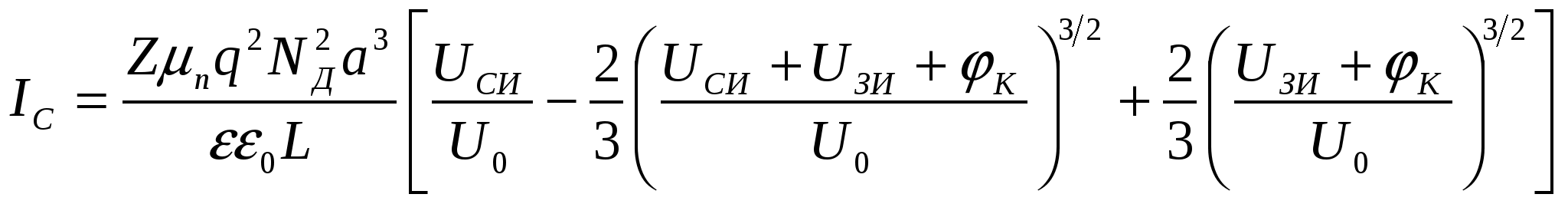

(7.19)

Выражение (7.19) можно представить в ином виде:

(7.20)

где

(7.21)

– проводимость прямоугольного образца n-типа с размерами или проводимость канала при отсутствии обедненного слоя.

Вместо (7.20) можно использовать выражения, в которые не вхо­дит отношение напряжений:

(7.22)

Выражение (7.22) позволяет определить токи стока при любых соот­ношениях напряжений U_си, U_зи и найти статические характеристики полевого транзистора.

7.2.2. Статические характеристики

Выходные характеристики. Идеализированные выходные ха­рактеристики I_с = f(U_cu) при U_зи = const, рассчитанные по формуле (7.22), изображены на рис. 7.3.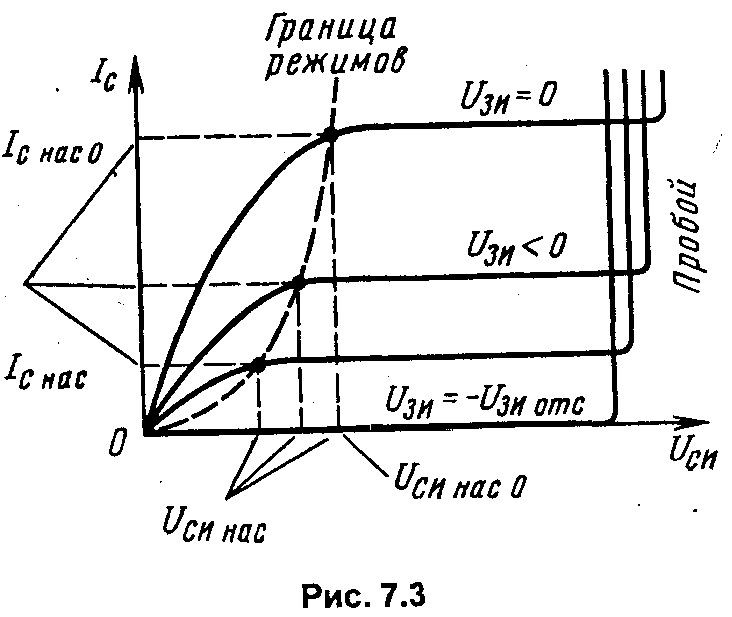

При отсутствии напряжения на электродах (U_си = U_зи = 0) ПТ на­ходится в термодинамическом равновесии, а токи электродов равны нулю. При фиксированном нулевом напряжении на за­творе (U_зи = 0) ток канала сначала линейно увеличи­вается с ростом напряже­ния U_си, затем скорость ро­ста уменьшается и при не­котором напряжении U_си рост прекращается. Это происходит при значении U_{си нас0} , соответствующем смыканию канала около стока (см. рис. 7.2,г). Напря­жение насыщения опреде­ляется по формуле (7.11).

Легко показать с помощью выражений (7.19), (7.20) или (7.22), что при любом фиксированном напряжении затвора (U_зи = const) ток стока проходит через максимальное значение, соответствующее ус­ловию dI_c/d U_си = 0. Это условие выполняется, когда наступает пере­крытие канала около стока, т.е. при U_си = U_{си нас0о}.

Подставив U_{си нас} из (7.11) в (7.22), получим значение тока (тока насыщения):

(7.23)

Формально из (7.22) при U_си > U_{си нас} после максимума должно начаться уменьшение тока. Однако вывод этот не правомочен. Дело в том, что уравнение (7.22) справедливо, пока не наступило перекрытие канала. При перекрытии канала у стока использован­ное при выводе уравнения для тока приближение плавного кана­ла становится неприменимым. Кроме того, становится неправдо­подобным и предположение о существовании резкой границы обедненной области, использованное для расчета ширины обед­ненной области (3.21), так как, когда сливаются два перехода, те­ряет смысл понятие перехода. В связи с неприменимостью фор­мулы (7.22) после наступления перекрытия канала у стока вопрос о величине тока при напряжениях U_си > U_{си нас} требует дополни­тельного рассмотрения.

Штриховая линия на рис. 7.3 ограничивает область применимо­сти выражения (7.19). Пересечение этой линии с расчетными харак­теристиками определяет для каждого заданного напряжения (пара­метра) U_зи напряжение U_{си нас}, при котором происходит перекрытие канала у стока, и соответствующие им токи насыщения I_{с нас}. В идеа­лизированной модели ток при U_си>U_{си нас} принимают равным току насыщения (7.23), т.е. считают верхние участки характеристик гори­зонтальными, а область этих участков – областью (режимом) насы­щения. Очевидно, что при U_си > U_{си нас} точка перекрытия канала смещается от стока в направлении к истоку и имеет, например, коор­динату х = L' < L (см. рис. 7.2, д). Интервал ∆L = L–L' определяет об­ласть перекрытия. Рассмотренная особенность называется эффек­том модуляции длины канала.

Таким образом, штриховая линия на рис. 7.3 соответствует нача­лу насыщения тока при различных значениях параметра U_зи. Как же объяснить существование тока в перекрытой области ∆L бывшего канала, но теперь области, обедненной носителями?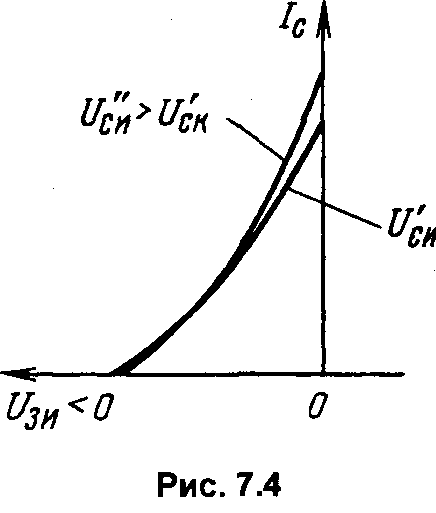

Дело в том, что на области перекрытия ∆L существует паде­ние напряжения, равное разности приложенного напряжения к стоку U_си и напряжения насыщения U_{си нас}, действующего меж­ду точкой перекрытия (х = L') и истоком: ∆U = U_си–U_{си нас}. Эта разность потенциалов создает продольное электрическое поле, которое складывается с полем обедненных областей переходов. Каждое поле в отдельности и результирующее поле являются ускоряющими для подходящих к области перекрытия из канала электронов. Ускоряющее поле переводит подошедшие электро­ны через область перекрытия к стоку, вызывая в этой области и в цепи стока ток.

Более того, экспериментально установлено, что с ростом U_си в области насыщения происходит некоторый рост тока стока. Объяс­нить это можно тем, что с ростом U_си реальная длина канала L' уменьшается, а напряжение на канале (на длине L') остается не­изменным, равным напряжению U_{си нас}. Напряженность продольно­го поля E_x в канале, а значит, и ток увеличиваются. Этот эффект осо­бенно сильно выражен в транзисторах с короткими каналами. В транзисторах с большой длиной канала (более 3...4 мкм) рост тока невелик и может быть учтен заменой в расчетных формулах (например, (7.19), (7.21)) величины L на L' < L.

Обратим теперь внимание на возмож­ность лавинного пробоя при дальнейшем увеличении U_си. Причиной пробоя явля­ются большие значения напряженности электрического поля, появляющиеся в переходе сток-затвор. Поля максималь­ны вблизи края затвора около стока. В этом месте происходит ударная генера­ция пар носителей электрон-дырка.

Электроны переносятся к стоку, а дырки двигаются к затвору, име­ющему отрицательный потенциал. В результате этого увеличива­ется обратный ток затвора (ток утечки), а также ток стока, как пока­зано на рис. 7.3. Напряжение лавинного пробоя U_{сз проб} является константой для прибора. Так как напряжение на переходе около стока равно сумме напряжений U_зии U_си, то очевидно, что с рос­том U_зи уменьшается напряжение U_си, при котором произойдет пробой. Поэтому в области лавинного пробоя наблюдается «пере­хлест» характеристик.

Стокозатворные (передаточные) характеристики. Это зави­симости тока стока от напряжения U_зи при фиксированных значени­ях напряжения U_си. Эти зависимости для U_си >U_{си нас} показаны на рис. 7.4. Они могут быть рассчитаны по формуле (7.23) в предполо­жении, что токи при U_си > U_{си нас} мало отличаются от I_{с нас}, харак­терного для начала области насыщения.

Для упрощения можно пренебречь контактной разностью потен­циалов φ_к. Тогда из (7.23)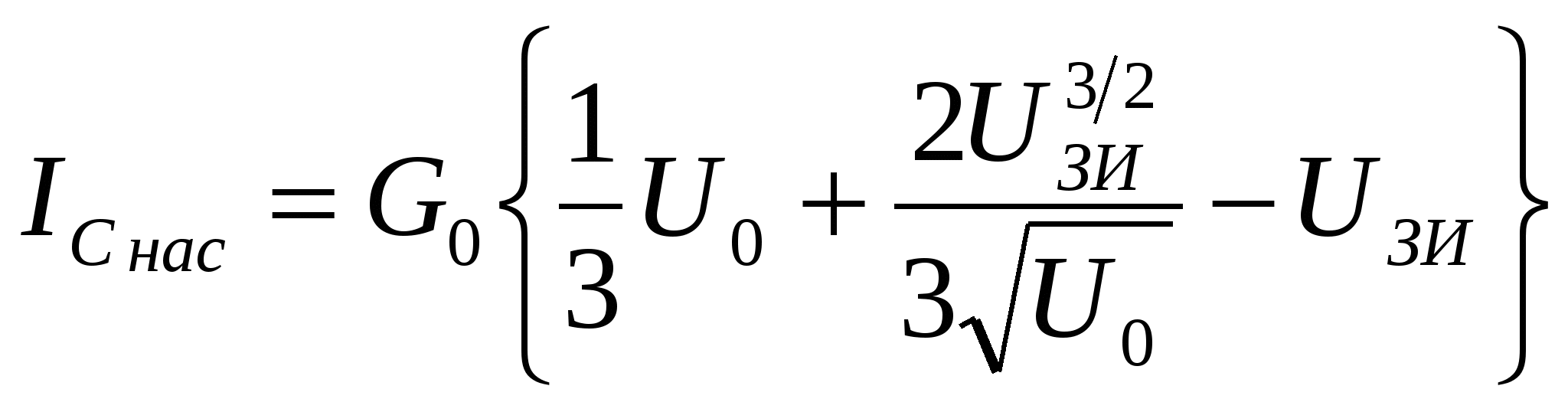

(7.24)

При U_зи = 0

(7.25)

и вместо (7.24) можно записать

(7.26)

Результаты, относящиеся к ВАХ транзисторов, были получе­ны для варианта исполнения, когда распределение концентрации примесей в объеме канала однородное. В реальных транзисторах с р-n-переходом распределение легирующих примесей в пределах канала по толщине (ось у)­ может быть разным и находится между двумя предельными случаями (рис. 7.5): однородным распределением 1, когда они равномерно распределены во всем объеме канала, и распределени­ем 4, когда основная часть примесей сосредоточена в узкой области около оси канала (так называемое пиковое распределение). Кривые 2 и 3 относят­ся к линейному и экспоненциальному распределению соответственно.

Кроме распределения примеси важную роль играет распре­деление подвижного заряда, создающее ток в канале, по толщи­не канала. Контактная разность потенциалов р-n-перехода и внешние напряжения на электродах транзистора приводят к то­му, что из канала будут удаляться именно свободные носители, а не обеспечивающие их появление атомы примеси. Свободные носители заряда в большинстве конструкций приборов сосредо­точены около оси канала, а их закон распределения будет отли­чаться от закона распределения примесей. В работе [29] указы­вается, что распределение носителей канала по оси у, перпенди­кулярной к оси канала, будет иметь пик, т.е. носители будут со­средоточены в узкой области около оси канала независимо от ха­рактера распределения примесей (от технологии изготовления прибора). Здесь же приведено решение для предельного случая такого распределения. Ток стока в этом случае описывается вы­ражением

(7.27)

которое справедливо в ненасыщенном режиме (крутые участки вы­ходных ВАХ). В точке насыщения, когда выполняется условие (7.11), ток насыщения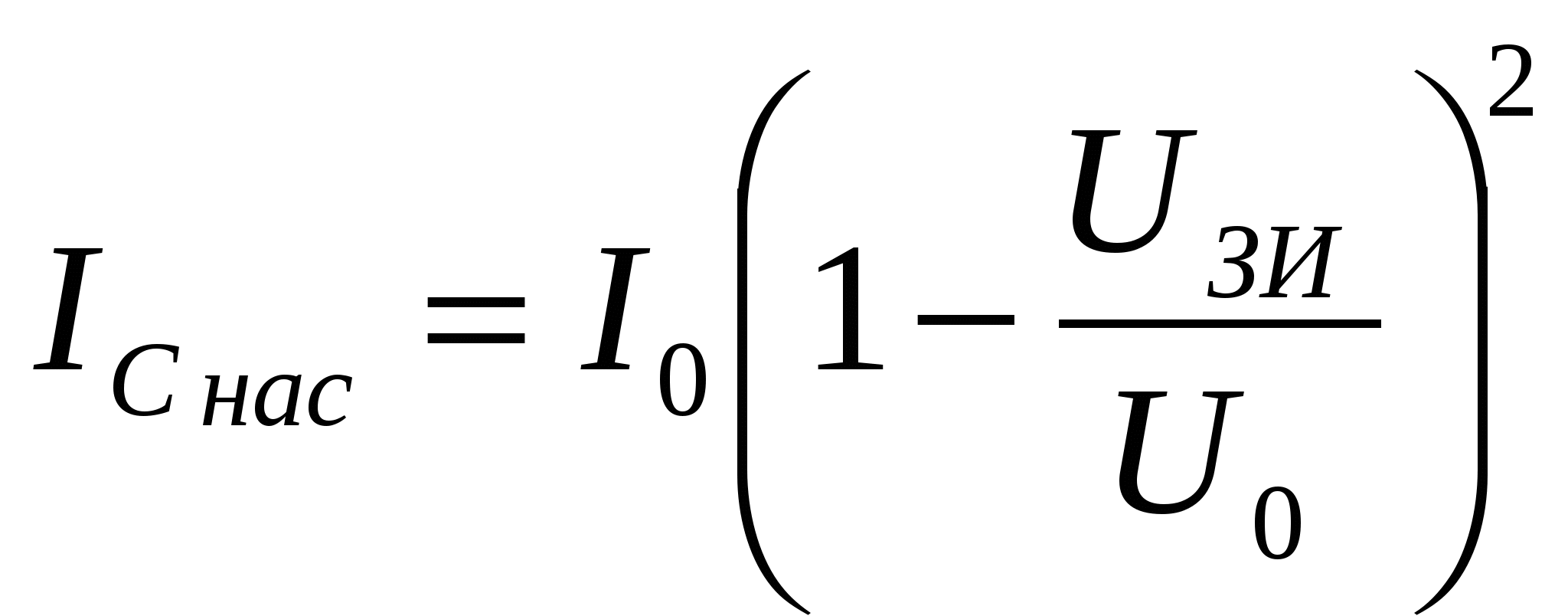

(7.28)

Сравним аналогичные выражения (7.26) и (7.28). Величина тока насыщения в (7.28) при U_зи= 0 I_{с нас} = I₀. При выводе форму­лы (7.28) за I₀ принята величина в 3 раза больше, чем I_{с нас} в фор­муле (7.25). Такое различие связано с разными принятыми зако­нами распределения заряда в канале. Уравнение (7.28) парабо­лическое. Если построить графики по уравнениям (7.26) и (7.28) в одной системе координат, то окажется, что пределы, в которых изменяются характеристики передачи в относительном масшта­бе I_{с нас}/I_{с нас0}, малы.

Ввиду простоты квадратичной (параболической) зависимости (7.28) по сравнению с (7.26) ее очень удобно применять для пред­ставления характеристик прямой передачи полевого транзистора при инженерных расчетах. Позже мы увидим, что квадратичный вид зависимости существует и в МДП-транзисторах, которые ис­следованы более подробно. Поэтому из теории последних прибо­ров ряд результатов можно перенести на полевые транзисторы с управляющим р-n-переходом с пиковым распределением подвиж­ного заряда в канале.