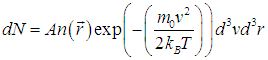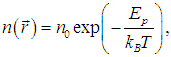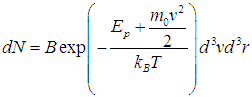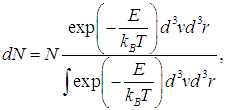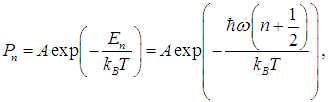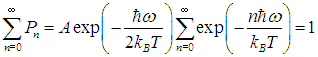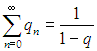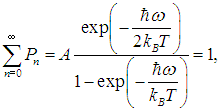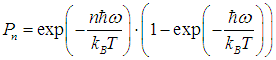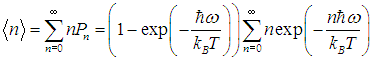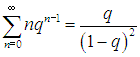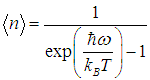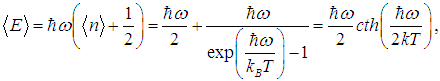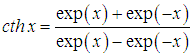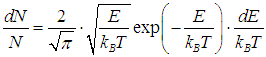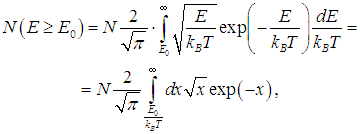13 Распределение Молекул по скоростям. Положение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют

• Название: Положение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют
• Дата: 29.04.2023
• Размер: 0.61 Mb.
• Имя файла: 13 Распределение Молекул по скоростям.docx
• Тип: Закон; #1097495
• страница: 3 из 3

3.5. Распределение Максвелла — Больцмана

Мы установили функцию, описывающую распределение молекул по скоростям (распределение Максвелла), и зависимость, характеризующую распределение молекул по значениям потенциальной энергии (распределение Больцмана). Обе зависимости можно объединить в одно обобщенное распределение.

 

Рассмотрим бесконечно малый объем dV газа, расположенный в точке с радиусом-вектором   в большой системе, представляющей идеальный газ при постоянной температуре во внешних силовых полях. Число молекул в выделенном объеме есть n(   ) d³r. Поскольку объем невелик, в его пределах плотность частиц можно считать постоянной. Это означает, что выполнено условие справедливости распределения Максвелла. Тогда для числа молекул dN, имеющих скорости от v до v + dv и находящихся в объеме d³r, в результате объединения зависимостей (3.11) и (3.27), получаем следующую формулу:

(3.54)

 

Но концентрация молекул n(r) зависит от расположения этого объема во внешних силовых полях:

(3.55)

где n₀ — концентрация молекул в точке, где Е_p = 0. Тогда

(3.56)

Поскольку выражение

(3.57)

представляет собой полную энергию частицы во внешнем потенциальном силовом поле, мы приходим к обобщенному распределению Максвелла — Больцмана по энергиям молекул:

(3.58)

 

где N — полное число частиц в системе, a dN — число частиц с координатами между r и r + dr и (одновременно) со скоростями между v и v + dv.  

Средняя энергия квантового осциллятора. Распределение Максвелла — Больцмана было получено в классической физике, но оно оказалось справедливым и в квантовой механике, где были подвергнуты пересмотру многие казавшиеся незыблемыми положения. В качестве примера рассмотрим задачу о грузе массой т, закрепленном на конце пружинки с жесткостью k. Уравнение движения хорошо известно, и его решением являются гармонические колебания тела с круговой частотой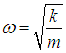



Классическая энергия системы, моделирующей колебания атомов в молекуле дается формулой (3.62) и может принимать любые значения в зависимости от амплитуды колебаний. Как нам известно из квантовой механики, энергия колебаний квантуется, то есть принимает дискретный ряд значений, определяемых формулой: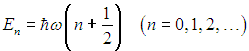



В соответствии с общими принципами статистической физики вероятность Р_n найти осциллятор в состоянии, характеризуемом неким значением n колебательного квантового числа, определяется формулой

(1)

где А — нормировочная постоянная. Для ее определения надо воспользоваться условием нормировки вероятности

(2)

Для этого в известную формулу для геометрической прогрессии

(3)

подставим значение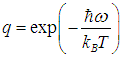



Получаем тогда вместо (2)

(4)

откуда следует выражение для постоянной А. Используя его в выражении (1), приходим к вероятности

(5)

Видно, что чем больше значение квантового числа n, тем меньше вероятность обнаружить осциллятор в таком состоянии. Чем выше температура, тем большие значения n становятся практически значимыми для системы. При



к нулю стремятся все вероятности Р_n с n > 1, и лишь



Иными словами, при нулевой температуре нет тепловых возбуждений, и осциллятор совершает «нулевые колебания» — находится в основном состоянии с наименьшей энергией



Распределение осцилляторов по энергиям в зависимости от температуры системы показано на рис. 3.9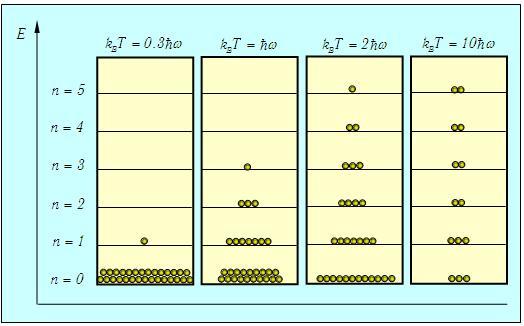



Рис. 3.9. Примерное распределение N = 30 квантовых осцилляторов по энергетическим уровням в зависимости от температуры. Показаны только основной и пять первых возбужденных уровней энергии. При Т = 0 все осцилляторы находятся в основном состоянии. По мере роста температуры становятся доступными все более высокие энергии, и распределение осцилляторов по уровням становится все более равномерным

Для наглядности мы взяли систему из небольшого (N = 30) числа осцилляторов (строго говоря, статистические законы применимы к системам с гораздо большим числом частиц).

 

Возникает вопрос: каково среднее значение  колебательного квантового числа n при некоторой температуре T? Для ответа мы должны подсчитать сумму:

(6)

Чтобы сделать это, продифференцируем по q обе части равенства (3.67) для геометрической прогрессии: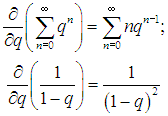



откуда получаем

(7)

Используя (7) при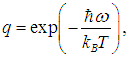



получаем из (6) выражение для искомого среднего

(8)

 

Теперь легко получить среднюю энергию осциллятора

(9)

где функция cth — гиперболический котангенс определена соотношением

(10)

На рис. 3.10 сплошной линией изображена средняя энергия квантового осциллятора, измеренная в единицах ħω,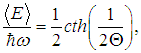



в зависимости от «безразмерной температуры»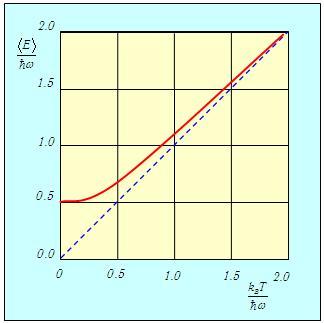





Рис. 3.10. Средняя энергия квантового осциллятора в зависимости от температуры

Пунктирная линия



соответствует результату классической физики. Действительно, энергия



приходящаяся на одну степень свободы, является средним значением как кинетической, так и потенциальной энергий классического осциллятора, так что среднее значение полной энергии как раз равно



Видно, что квантовые поправки важны при низких температурах: при q < 0,3 средняя энергия осциллятора близка к энергии основного состояния ħω/2. В таком случае говорят, что колебательные степени свободы «заморожены», то есть тепловой энергии недостаточно для возбуждения колебаний. Но уже при q = 2 обе энергии практически совпадают, то есть квантовые поправки малы. Значение q = 1 можно принять за условную границу между квантовой и классическими областями. Ее смысл прозрачен: при



тепловая энергия равна минимальной энергии возбуждения осциллятора, то есть разности между энергией



первого возбужденного состояния и энергией



основного состояния осциллятора.

 

Какие же температуры можно считать низкими для осциллятора, моделирующего реальную систему, например молекулу водорода Н₂? Характерные частоты молекулярных колебаний располагаются обычно в инфракрасной области и имеют порядок n = 10¹⁴ Гц. Этому соответствуют энергия



и температура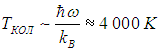



Средняя энергия квантового ротатора. Таким образом, привычные для нас комнатные температуры оказываются достаточно низкими с точки зрения возбуждения колебаний молекул. Посмотрим, что происходит с молекулами при температурах Т < Т_К0Л. Так как колебания отсутствуют, двухатомную молекулу можно представить в виде «гантели» — двух атомов, жестко соединенных между собой. Такая система называется ротатором и, как мы видели ранее, имеет пять степеней свободы - три поступательных (движение центра масс) и две вращательных. Энергия вращательного движения классического ротатора имеет вид (3.61). Учитывая связь

 

между угловой частотой вращения ω, моментом инерции I и моментом импульса L, записываем классическую энергию вращения молекулы как



В квантовой механике квадрат момента импульса квантуется,



Здесь J — ротационное квантовое число, поэтому квантуется и энергия вращательного движения молекулы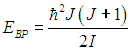



Используя это соотношение и распределение Максвелла — Больцмана, можно получить выражение для средней энергии квантового ротатора. Однако в этом случае формулы достаточно сложны, и мы ограничимся качественными результатами. При высоких температурах средняя энергия стремится к классическому значению k_BТ, соответствующему двум степеням свободы (вращение вокруг двух ортогональных осей). При низких температурах ротатор будет находиться в основном состоянии, соответствующем значению J = 0 (отсутствие вращения). «Переход» между двумя этими предельными случаями осуществляется, очевидно, при такой температуре Т_ВР когда тепловое движение способно возбудить вращательные степени свободы. Минимальная (отличная от нуля) энергия вращения равна



как это следует из формулы для Е_ВР при J = 1. Поэтому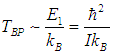



Для момента инерции молекулы можно принять оценку



где m_р = 1,67·10^–27 кг (масса протона), а а_В = 5·10^–11 м — радиус Бора. Получаем тогда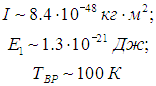



Полученные оценки подтверждаются измерениями молярной теплоемкости при постоянном объеме с_nV, которые мы уже обсуждали в предыдущей главе. При температурах ниже 100 К в тепловом движении участвуют только поступательные степени свободы молекулы. Средняя энергия молекулы равна 3kBТ/2, а энергия одного моля — 3N_Ak_BT/2=3RT/2, откуда следует выражение для теплоемкости с_nV = 3R/2. В диапазоне температур от 100 К до 200 К молярная теплоемкость увеличивается до значения с_nV = 5R/2, что свидетельствует о «размораживании» двух дополнительных (вращательных) степеней свободы (то есть о добавлении k_BT энергии на молекулу). В районе температур от 4 000 К до 5 000 К молярная теплоемкость снова увеличивается, на этот раз до значения с_nV = 7R/2. Это «разморозилась» колебательная степень свободы, что принесло дополнительную энергию k_BT на молекулу.

 

Скорость химических реакций. У химиков есть эмпирическое правило, что при повышении температуры на 10 °С скорость реакции удваивается. Это — всего лишь грубое обобщение, из него есть множество исключений, но все же в целом оно более или менее верно. Объяснение можно и здесь дать на основе распределения Максвелла — Больцмана.

 

Для протекания многих химических реакций необходимо, чтобы энергия участвующих в них частиц превышала некое пороговое значение, которое мы обозначим Е₀. Чем больше таких частиц, тем выше скорость реакции. Из формул (3.28), (3.29) следует распределение частиц по энергиям. В них надо лишь выразить скорость частицы v через ее кинетическую энергию Е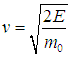



и учесть, что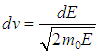



В результате получаем распределение частиц по энергиям

(11)

Отсюда находим число частиц с энергией Е > Е₀:

(12)

где мы сделали замену переменных интегрирования



Для численных оценок мы примем пороговую энергию равной энергии возбуждения колебаний молекулы: Е₀ = 6·10^–20 Дж. Тогда для комнатной температуры Т₁ = 300 К получаем величину E₀/k_BT₁ = 14,5, а для температуры Т₂ = 310 К это отношение равно Е₀/k_BТ₂ = 14,0. Числа частиц, участвующих в реакции, определяются соотношениями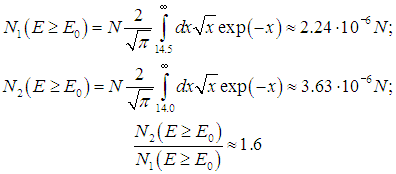



Действительно, повышение температуры всего на 10 градусов привело к увеличению на 60 % числа частиц, энергия которых превышает пороговое значение.