Полупроводниковые диоды. Полупроводниковый диод

Название	Полупроводниковый диод
Анкор	Полупроводниковые диоды.docx
Дата	09.02.2018
Размер	1.64 Mb.
Формат файла
Имя файла	Полупроводниковые диоды.docx
Тип	Документы #15375
страница	7 из 15

1 2 3 4 5 6 7 8 9 10 ... 15

Применение[править | править исходный текст]

Метод эквивалентного генератора используется при расчёте сложных схем, в которых одна ветвь выделяется в качестве сопротивления нагрузки, и требуется исследовать и получить зависимость токов в цепи от величины сопротивления нагрузки.

В соответствии с данным методом неизменная часть схемы преобразовывается к одной ветви, содержащей ЭДС и внутреннее сопротивление эквивалентного генератора.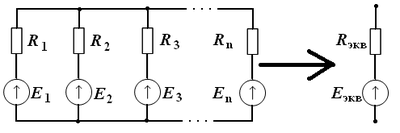

http://upload.wikimedia.org/wikipedia/commons/thumb/1/1f/equivalent_generator.png/400px-equivalent_generator.png

Применение метода эквивалентного генератора

ЭДС эквивалентного генератора определяется по формуле:

$e_{eqv} = \frac {\sum^{n}_{i=1} {e_i g_i}}{\sum^{n}_{i=1} {g_i}} = \frac{{e_1 g_1} + {e_2 g_2} + {e_3 g_3} + ... + {e_i g_i}}{g_1 + g_2 + g_3 + ... + g_i},$

где: — проводимость участка цепи, равная

Для определения эквивалентного сопротивления генератора применяется расчет последовательно и параллельно соединённых сопротивлений, а также, в случае более сложных схем, применяют преобразование треугольник-звезда.

После определения параметров эквивалентного генератора можно определить ток в нагрузке при любом значении сопротивления нагрузки по формуле:

$i_h = \frac{e_{eqv}}{r_{eqv} + r_h}.$

Любой сколь угодно сложный активный двухполюсник можно представить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на зажимах двухполюсника, а внутреннее сопротивление равно входному сопротивлению пассивного двухполюсника со стороны тех же зажимов.При определении входного сопротивления все источники должны быть заменены своими внутренними сопротивлениями – источники ЭДС закорачиваются, а источники тока размыкаются.

Метод узловых потенциалов.

Метод узловы́х потенциалов — метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.

Теоретические основы[править | править исходный текст]

Если в цепи, состоящей из У узлов и Р рёбер, известны все характеристики звеньев (полные сопротивления R, величины источников ЭДС E и тока J), то возможно вычислить токи I_i во всех рёбрах и потенциалы φ_i во всех узлах. Поскольку электрический потенциал определён с точностью до произвольного постоянного слагаемого, то потенциал в одном из узлов (назовём его базовым узлом) можно принять равным нулю, а потенциалы в остальных узлах определять относительно базового узла. Таким образом, при расчёте цепи имеем У+Р–1 неизвестных переменных: У–1 узловых потенциалов и Р токов в рёбрах.

Не все из указанных переменных независимы. Например, исходя из закона Ома для участка цепи, токи в звеньях полностью определяются потенциалами в узлах:

$\ i_i = \frac{\phi_a-\phi_b+e_i}{r_i} + j_i.$

С другой стороны, токи в рёбрах однозначно определяют распределение потенциала в узлах относительно базового узла:

$\ \phi_b = \phi_a + e_i + (j_i-i_i)r_i.$

Таким образом, минимальное число независимых переменных в уравнениях цепи равно либо числу звеньев, либо числу узлов минус 1, в зависимости от того, какое из этих чисел меньше.

При расчёте цепей чаще всего используются уравнения, записываемые, исходя из законов Кирхгофа. Система состоит из У–1 уравнений по 1-му закону Кирхгофа (для всех узлов, кроме базового) и К уравнений по 2-му закону Кирхгофа для каждого независимого контура. Независимыми переменными в уравнениях Кирхгофа являются токи звеньев. Поскольку согласно формуле Эйлера для плоского графа число узлов, рёбер и независимых контуров связаны соотношением

$\ y - p + k = 1$

или

$\ p = y + k - 1,$

то число уравнений Кирхгофа равно числу переменных, и система разрешима. Однако число уравнений в системе Кирхгофа избыточно. Одним из методов сокращения числа уравнений является метод узловых потенциалов. Переменными в системе уравнений являются У–1 узловых потенциалов. Уравнения записываются для всех узлов, кроме базового. Уравнения для контуров в системе отсутствуют.

Уравнение для потенциала в узлах[править | править исходный текст]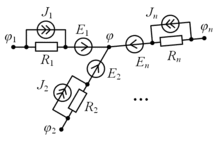

http://upload.wikimedia.org/wikipedia/commons/thumb/1/1f/%d0%a4%d1%80%d0%b0%d0%b3%d0%bc%d0%b5%d0%bd%d1%82_%d1%86%d0%b5%d0%bf%d0%b8.gif/220px-%d0%a4%d1%80%d0%b0%d0%b3%d0%bc%d0%b5%d0%bd%d1%82_%d1%86%d0%b5%d0%bf%d0%b8.gif

Рис. 1. Фрагмент цепи: узел с примыкающими звеньями

Рассмотрим фрагмент цепи, состоящий из узла и примыкающих к нему звеньев (рис. 1). Согласно 1-му закону Кирхгофа сумма токов в узле равна нулю:

$\sum_{i=1}^n i_i = 0.$

Ток в звене определим, исходя из закона Ома для участка цепи:

$i_i = \frac{\phi_i-\phi+e_i}{r_i} + j_i$

откуда

$\sum_{i=1}^n \left( \frac{\phi_i-\phi+e_i}{r_i} + j_i \right) = 0;$

$\phi \sum_{i=1}^n \frac{1}{r_i} - \sum_{i=1}^n \frac{\phi_i}{r_i} = \sum_{i=1}^n \left( \frac{e_i}{r_i} + j_i \right).$

Обозначив проводимости рёбер через

получим окончательное уравнение для узла

$\phi \sum_{i=1}^n y_i - \sum_{i=1}^n \phi_i y_i = \sum_{i=1}^n (e_i y_i + j_i).$

Последнее уравнение получено, исходя из предположения, что все источники тока и ЭДС направлены в сторону рассматриваемого узла. Если какой-либо источник направлен в противоположную сторону, его ЭДС или ток необходимо взять с обратным знаком.

Записав последнее уравнение для каждого узла цепи, кроме базового, получим систему уравнений для узловых потенциалов.

Метод контурных токов.

Ме́тод ко́нтурных то́ков — метод сокращения размерности системы уравнений, описывающей электрическую цепь.
Метод контурных токов — метод расчёта электрических цепей, при котором за неизвестные принимаются токи в контурах, образованных некоторым условным делением электрическую цепь

1 2 3 4 5 6 7 8 9 10 ... 15