Задачи по моделированию. Помощь с дистанционным обучением
 Скачать 303.87 Kb. Скачать 303.87 Kb.
|
|
Работа выполнена авторами сайта ДЦО.РФ Помощь с дистанционным обучением:тесты, экзамены, сессия.Почта для заявок: INFO@ДЦО.РФМоделирование систем массового обслуживания 2.1 Одноканальная система массового обслуживанияЗадачиВыполните имитацию работы банка, осуществляющего прием вкладов. Размер депозита является случайной величиной с нормальным законом распределения (среднее значение - 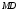 ; среднее квадратическое отклонение - ; среднее квадратическое отклонение - 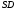 ). Время между приходом двух вкладчиков – случайная величина с показательным законом распределения (среднее значение - ). Время между приходом двух вкладчиков – случайная величина с показательным законом распределения (среднее значение - 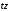 ), а время обслуживания равномерно распределено на интервале [a;b]. Пусть исходные значения равны величинам: ), а время обслуживания равномерно распределено на интервале [a;b]. Пусть исходные значения равны величинам: 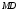 =30000 руб.; =30000 руб.; 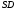 =10000 руб.; =10000 руб.; 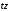 =1 час; a=20 мин.; b=30 мин.; =1 час; a=20 мин.; b=30 мин.; 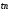 =9 ч., число заявок равно 5. Определите время прихода последнего клиента, среднее время пребывания клиента в системе. Какой общий размер вкладов будет осуществлен а) после прихода пяти клиентов; б) к моменту времени 12:00 ч.? =9 ч., число заявок равно 5. Определите время прихода последнего клиента, среднее время пребывания клиента в системе. Какой общий размер вкладов будет осуществлен а) после прихода пяти клиентов; б) к моменту времени 12:00 ч.?  Рис.2.7 – Система массового обслуживания «Банк» Проведите 10 экспериментов и рассчитайте величины: среднее время ожидания; среднее число обслуженных заявок за период с 9:00 до 15:00 ч. Предположите, что 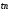 =0 и выполните имитацию описанным на рис. 2.3 способом. =0 и выполните имитацию описанным на рис. 2.3 способом. Пусть банковская автоматизированная система может выходить из строя, что приводит к необходимости вызова специалистов, устраняющих неполадку. Выполните имитацию периодов нормальной работы системы и ее ремонта, если данные величины являются случайными с показательным законом распределения, а 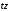 =30 дней, =30 дней, 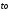 =3 ч. Рассмотрите процесс поступления 5 заявок (отказов). =3 ч. Рассмотрите процесс поступления 5 заявок (отказов).2.2 Двухканальная система массового обслуживанияЗадачиМагазин, располагающий двумя кассами, занимается продажей продовольственных товаров (рис. 2.10). Время между приходом двух покупателей – случайная величина с показательным законом распределения (среднее значение -tz), а время обслуживания равномерно распределено на интервале [a;b]. Сумма покупки является случайной величиной с нормальным законом распределения (среднее значение - 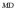 ; среднее квадратическое отклонение -SD). Пусть исходные значения равны величинам: MD=400 руб.; SD=100 руб.; tz=10 мин.; a=3 мин.; b=7 мин.; tn=9 ч. Выполните моделирование поступления семи заявок (покупателей). Определите время прихода седьмого клиента. Какой размер выручки получит магазин а) после того, как было обслужено семь покупателей; б) к моменту времени 10:00 ч.? ; среднее квадратическое отклонение -SD). Пусть исходные значения равны величинам: MD=400 руб.; SD=100 руб.; tz=10 мин.; a=3 мин.; b=7 мин.; tn=9 ч. Выполните моделирование поступления семи заявок (покупателей). Определите время прихода седьмого клиента. Какой размер выручки получит магазин а) после того, как было обслужено семь покупателей; б) к моменту времени 10:00 ч.?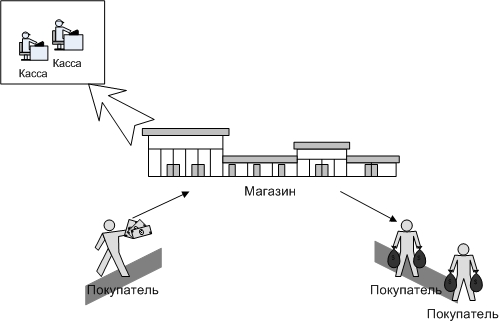 Рис.2.10 – Система массового обслуживания «Магазин» Предположите, что рассматриваемый поток клиентов – это потенциальные покупатели, которые с вероятностью  могут совершить покупку ( могут совершить покупку ( =0,6). =0,6). Пусть время обслуживания – дискретная случайная величина со следующим законом распределения
Выполните имитацию, учитывая данное условие. Проведите 10 экспериментов и рассчитайте величины: среднее время ожидания; средний размер выручки. 2.3 Система массового обслуживания с ограниченным по времени ожиданиемЗадачиМенеджер фирмы принимает заказы от клиентов на выполнение различных работ (рис.2.14). Заказы поступают посредством телефонной связи. Время между двумя звонками является случайной величиной с показательным законом распределения (среднее значение -  ), время обслуживания (принятия заказа) – случайная величина с нормальным законом распределения (среднее значение - ), время обслуживания (принятия заказа) – случайная величина с нормальным законом распределения (среднее значение -  , среднее квадратическое отклонение - , среднее квадратическое отклонение - 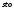 ). В том случае, если звонок поступил в то время, когда менеджер занят приемом другого заказа, то он получает отказ в обслуживании. Стоимость заказа клиента равномерно распределена на интервале [ ). В том случае, если звонок поступил в то время, когда менеджер занят приемом другого заказа, то он получает отказ в обслуживании. Стоимость заказа клиента равномерно распределена на интервале [ ; ;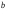 ]. Выполните моделирование данной системы при следующих исходных данных: ]. Выполните моделирование данной системы при следующих исходных данных:  =15 мин.; =15 мин.;  =15 мин.; =15 мин.; 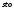 =2 мин.; =2 мин.;  =5000 руб.; =5000 руб.; 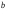 =15000 руб.; =15000 руб.;  =9 ч. Рассмотрите поступление шести звонков и определите следующие величины: число отказов в обслуживании; общая сумма заказов; время поступления последнего звонка. =9 ч. Рассмотрите поступление шести звонков и определите следующие величины: число отказов в обслуживании; общая сумма заказов; время поступления последнего звонка.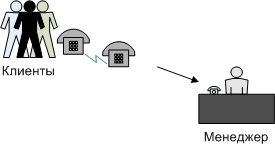 Рис.2.14 – Система обслуживания «Прием заказов» Проведите 10 экспериментов и рассчитайте величины: среднее число отказов в обслуживании; среднюю сумму заказов; среднее время завершения моделирования (время окончания обслуживания последней заявки). Выполните моделирование, считая, что вероятность совершения заказа клиентом равна  ( ( =0,7). =0,7). Предположите, что фирма наняла еще одного менеджера и вновь поступивший звонок направляется к свободному в данный момент работнику. Пусть новое оборудование фирмы позволяет поступившим звонкам ожидать освобождения менеджера в течение времени 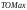 . Выполните моделирование при . Выполните моделирование при 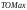 =2 мин. (число каналов обслуживания равно единице), рассчитайте среднее число отказов (за 10 реализаций) и сравните данное значение с полученным во втором задании. =2 мин. (число каналов обслуживания равно единице), рассчитайте среднее число отказов (за 10 реализаций) и сравните данное значение с полученным во втором задании.Рассмотрите ситуацию, когда максимальное время ожидания каждой заявки определяется также поведением клиентов и его значение – случайная величина с дискретным законом распределения:
2.4 Система массового обслуживания с очередьюЗадачиПарикмахерская занимается обслуживанием клиентов (рис. 2.17). Время между приходом двух клиентов является случайной величиной с показательным законом распределения (среднее значение -  ), а время обслуживания распределено по нормальному закону. В том случае, если в момент прихода нового клиента мастер занят, то клиент встает в очередь. При этом имеются места ожидания, число которых равно ), а время обслуживания распределено по нормальному закону. В том случае, если в момент прихода нового клиента мастер занят, то клиент встает в очередь. При этом имеются места ожидания, число которых равно 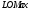 . Если же все места заняты, то клиент уходит и не ждет обслуживания. Выручка от одного клиента, а также его время обслуживания зависит от типа прически. В таблице 2.1 приведены характеристики этих данных. . Если же все места заняты, то клиент уходит и не ждет обслуживания. Выручка от одного клиента, а также его время обслуживания зависит от типа прически. В таблице 2.1 приведены характеристики этих данных.Таблица 2.1 – Характеристики причесок
Кроме того, имеются следующие статистические данные о том, сколько людей выбрало тот или иной тип прически (всего 100 человек)
Выполните моделирование поступления 9 заявок, используя следующие исходные данные:  =20 мин.; =20 мин.; 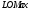 =2; =2;  =9 ч. =9 ч. 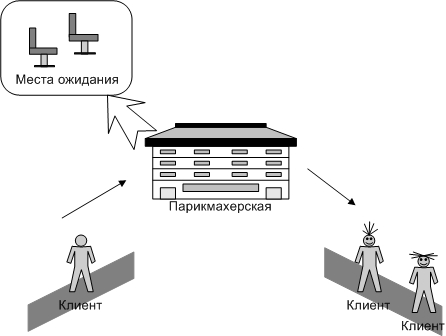 Рис. 2.17 - Система массового обслуживания «Парикмахерская» Рассчитайте следующие значения: максимальная длина очереди; общее время пребывания заявок в очереди; сумма выручки. Проведите 10 экспериментов и рассчитайте величины: среднее число отказов в обслуживании; среднюю выручку; среднее время завершения моделирования (время окончания обслуживания последней заявки). 2.5 Система с групповым обслуживанием заявокЗадачиВ парке развлечений расположен аттракцион, стоимость билета на который составляет  руб. (рис.2.20). Время между приходом двух желающих попасть на него является случайной величиной с показательным законом распределения (среднее значение равно руб. (рис.2.20). Время между приходом двух желающих попасть на него является случайной величиной с показательным законом распределения (среднее значение равно  ). Обслуживание начинается после того, как пришло ). Обслуживание начинается после того, как пришло 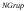 человек, а его продолжительность равна человек, а его продолжительность равна 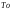 . Расходы, связанные с использованием аттракциона в течение времени обслуживания, равны . Расходы, связанные с использованием аттракциона в течение времени обслуживания, равны  руб. Выполните моделирование данной системы массового обслуживания при поступлении 10 заявок и исходных данных: руб. Выполните моделирование данной системы массового обслуживания при поступлении 10 заявок и исходных данных:  =50 руб.; =50 руб.;  =5 мин.; =5 мин.; 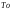 =10 мин.; =10 мин.; 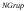 =3; =3;  =70 руб.; =70 руб.;  =9 ч.Рассчитайте общую выручку и прибыль, время ожидания, время прихода последнего клиента. =9 ч.Рассчитайте общую выручку и прибыль, время ожидания, время прихода последнего клиента.Используя различные значения 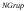 ( (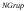 =1; 2; 3; 4), определите, как изменится прибыль и время ожидания. =1; 2; 3; 4), определите, как изменится прибыль и время ожидания. Проведите 10 экспериментов и найдите: среднее значение выручки; среднее значение общего времени ожидания; вероятность того, что общее время ожидания будет больше или равно 10 мин. 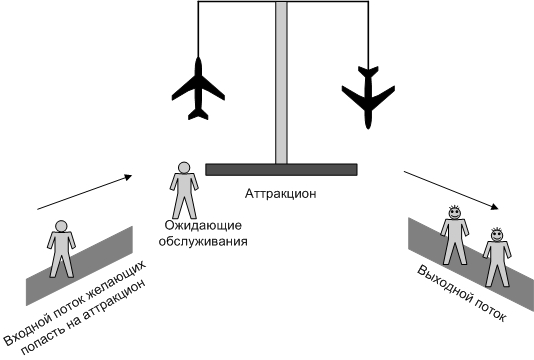 Рис.2.20 – Система массового обслуживания «Аттракцион» 2.6 Система массового обслуживания с групповым поступлением заявокЗадачиТакси занимается перевозкой людей (рис.2.22). Заявки от клиентов поступают через случайные промежутки времени, распределенные по показательному закону (среднее значение равно  ). Время доставки в одном направлении является случайной величиной, равномерно распределенной на интервале [ ). Время доставки в одном направлении является случайной величиной, равномерно распределенной на интервале [ ; ;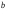 ]. Число клиентов с различными направлениями, осуществивших один вызов, может быть 1, 2 или 3. В этом случае доставка ведется по различным направлениям. Стоимость доставки зависит от числа направлений, по которым нужно доставить пассажиров. В таблице 2.2 приведены значения вероятности появления группы определенного размера и стоимость доставки. Выполните моделирование работы такси (пусть поступило 8 заявок), используя следующие исходные данные: ]. Число клиентов с различными направлениями, осуществивших один вызов, может быть 1, 2 или 3. В этом случае доставка ведется по различным направлениям. Стоимость доставки зависит от числа направлений, по которым нужно доставить пассажиров. В таблице 2.2 приведены значения вероятности появления группы определенного размера и стоимость доставки. Выполните моделирование работы такси (пусть поступило 8 заявок), используя следующие исходные данные:  =30 мин.; =30 мин.;  =15 мин.; =15 мин.; 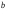 =30 мин.; =30 мин.;  =9 ч. Рассчитайте полученную таксистом выручку. =9 ч. Рассчитайте полученную таксистом выручку.Таблица 2.2 – Характеристики размера группы
Рассмотрите случай, когда оплата проезда производится пассажирами следующим образом: стоимость вызова равна 40 руб.; цена 1 мин. проезда составляет 40 руб. Проведите 10 экспериментов и рассчитайте: среднюю выручку; среднее время ожидания; вероятность того, что выручка будет менее 850 руб. 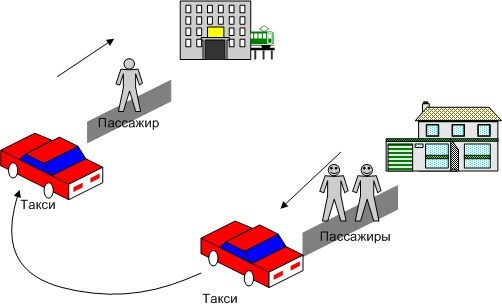 Рис. 2.22 – Система массового обслуживания «Такси» |
