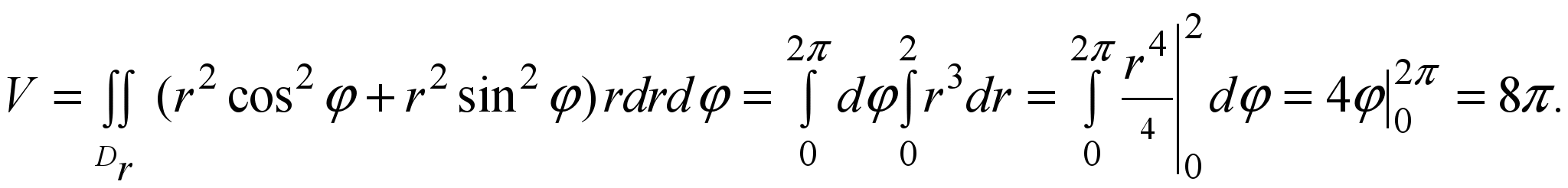Пусть задана область
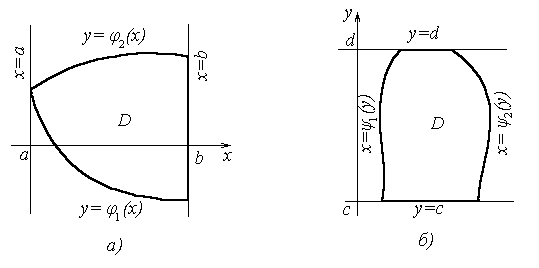
Рисунок 1
D ={(x, y): a ≤ x ≤ b, φ1(x)≤ y≤ φ2(x)} (6)
Область Dзаключена в полосе между прямыми x = a, y = b, снизу и сверху ограничена соответственно кривыми y = φ1(x) и y = φ2(x) .
Двойной интеграл (1) по области D (4) вычисляется переходом к повторному интегралу:
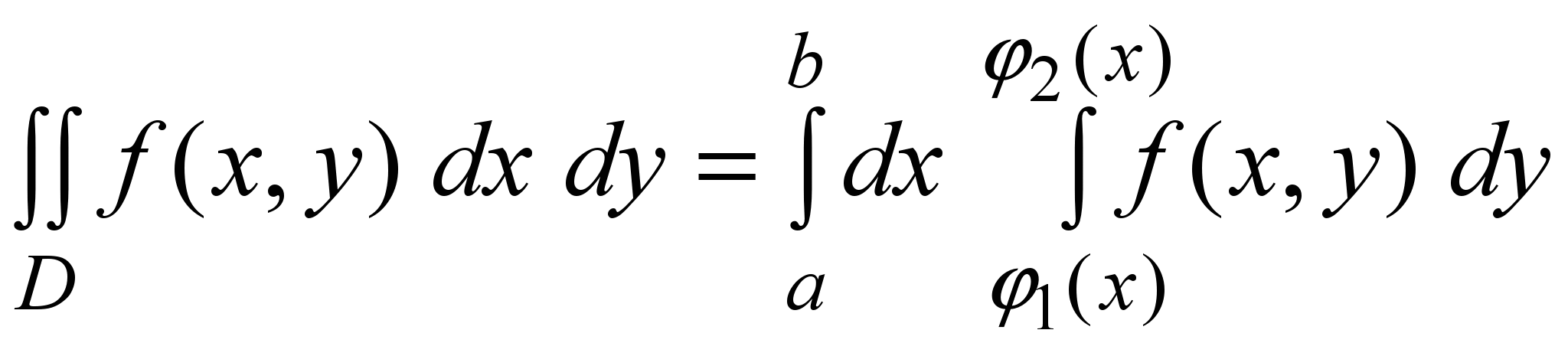 (7) (7)
Этот повторный интеграл вычисляется следующим образом. Сначала вычисляется внутренний интеграл
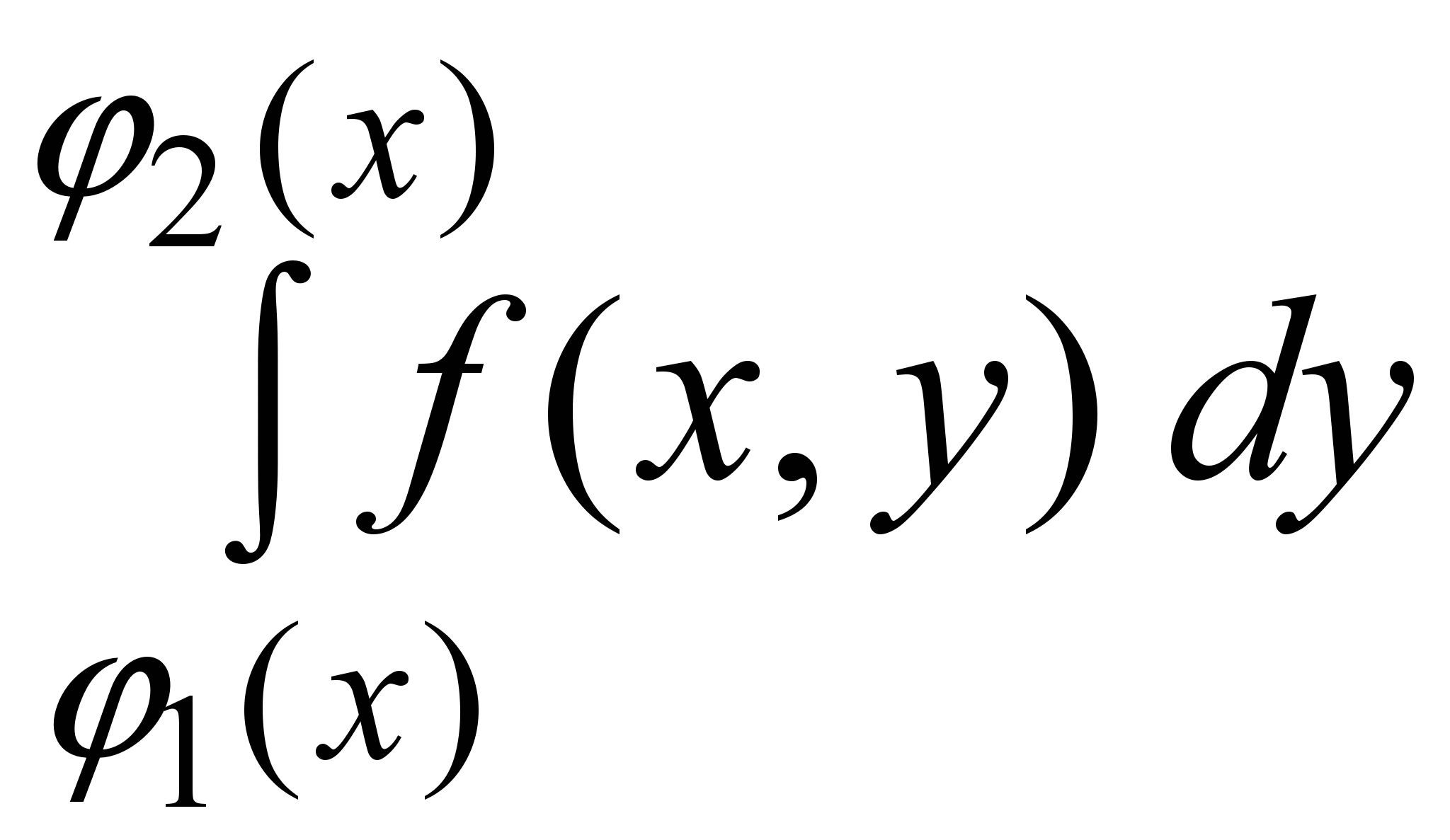
по переменной y, при этом x считается постоянной. В результате получится функция от переменной x, а затем вычисляется «внешний” интеграл от этой функции по переменной x.
Замечание. Процесс перехода к повторному интегралу по формуле (7) часто называют расстановкой пределов интегрирования в двойном интеграле. При расстановке пределов интегрирования нужно помнить два момента. Во-первых, нижний предел интегрирования не должен превышать верхнего, во-вторых, пределы внешнего интеграла должны быть константами, а внутреннего должны в общем случае зависеть от переменной интегрирования внешнего интеграла.
Пусть теперь область D имеет вид
D ={ (x, y) : c ≤ y ≤ d, ψ1(y)≤ x ≤ ψ2(y)} . (8)
Тогда
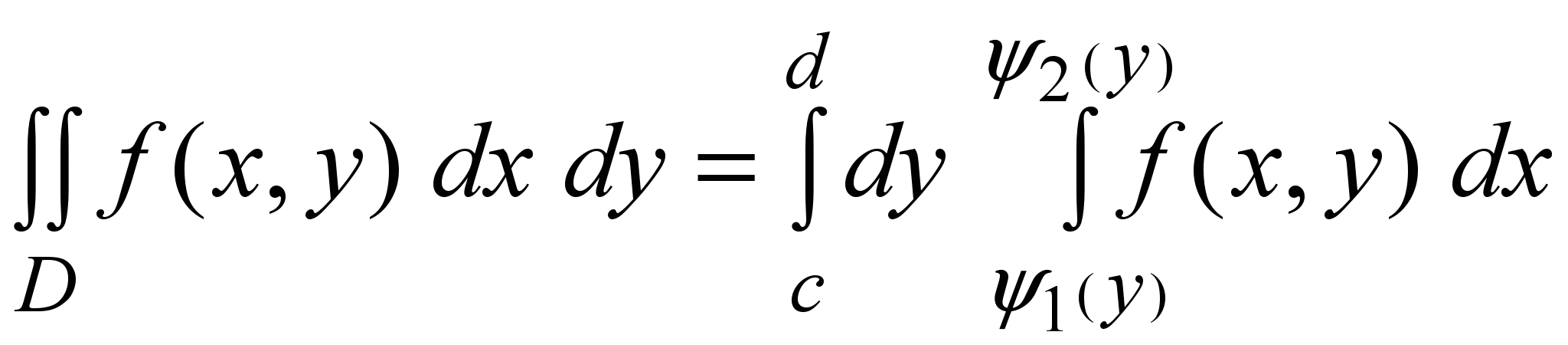 . (9) . (9)
Предположим, что область D можно представить в виде (6) и (8) одновременно. Тогда имеет место равенство
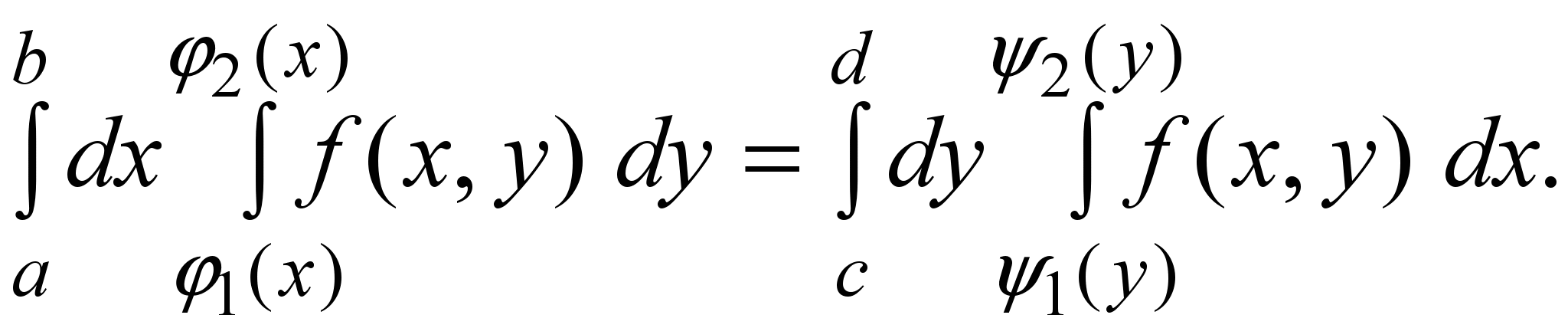 (10) (10)
Переход од одного повторного интеграла к другому в равенстве (10) называется изменением порядка интегрирования в двойном интеграле.
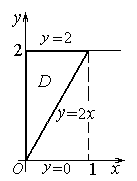
Примеры.
1) Изменить порядок интегрирования в интеграле
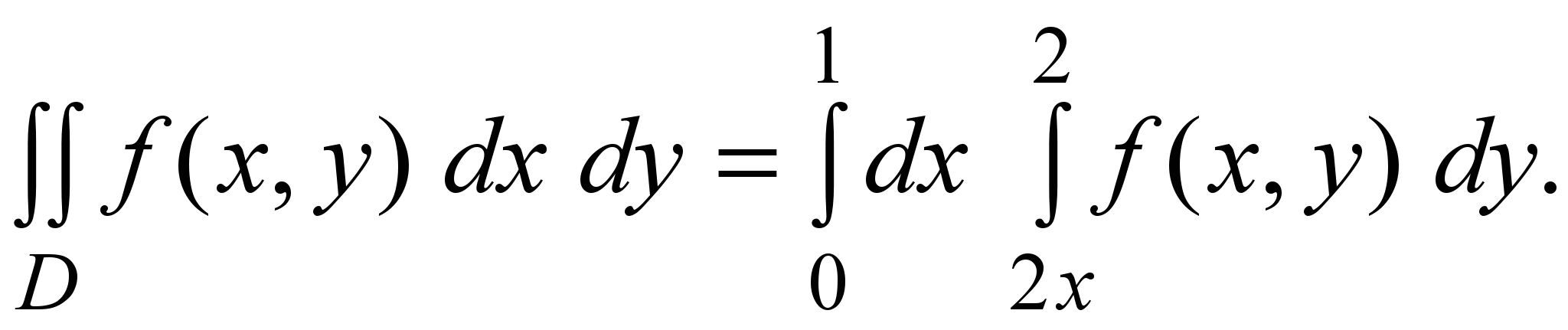
Решение. По виду повторного интеграла находим область
D ={(x, y): 0≤ x ≤1, 2x ≤ y≤2} .
Изобразим область D. По рисунку видим, что эта область расположена в горизонтальной полосе между прямыми y=0, y=2 и между линиями x =0и x = y 2. Это значит, что
D ={(x, y): 0≤ y ≤2, 0≤ x≤ y/2} .
Тогда по формуле (10) получаем
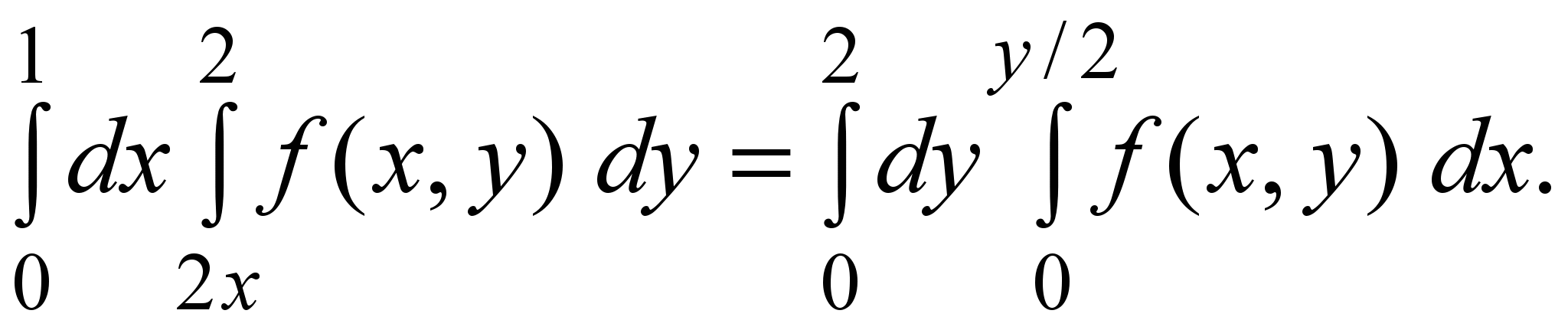
2)Вычислить интеграл 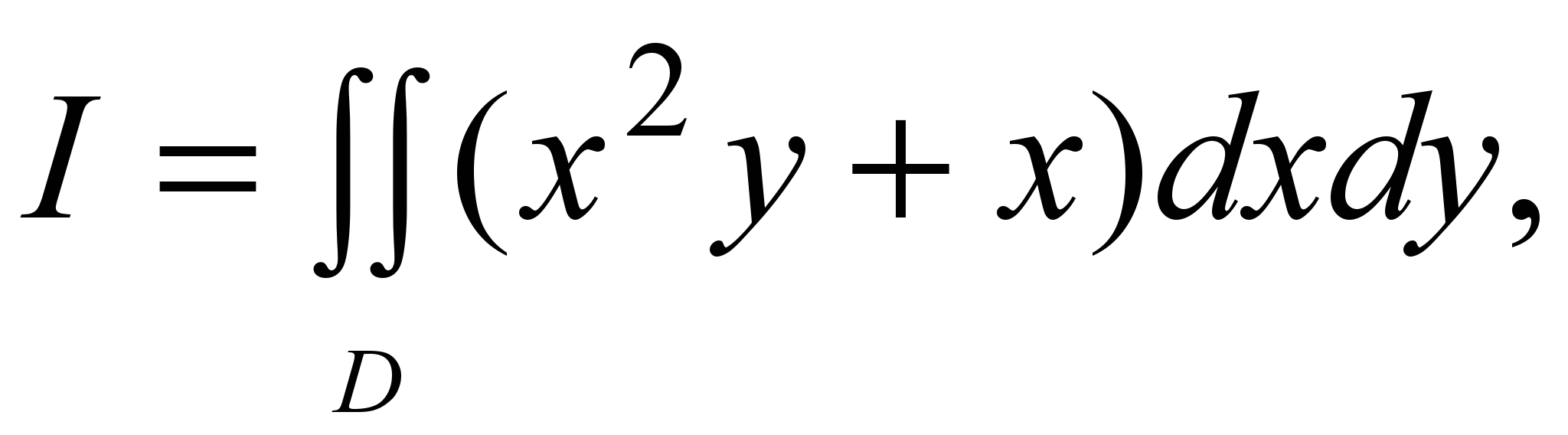 где D область из примера 1. где D область из примера 1.
Решение. Расставим пределы интегрирования в интеграле подобно примеру 1:
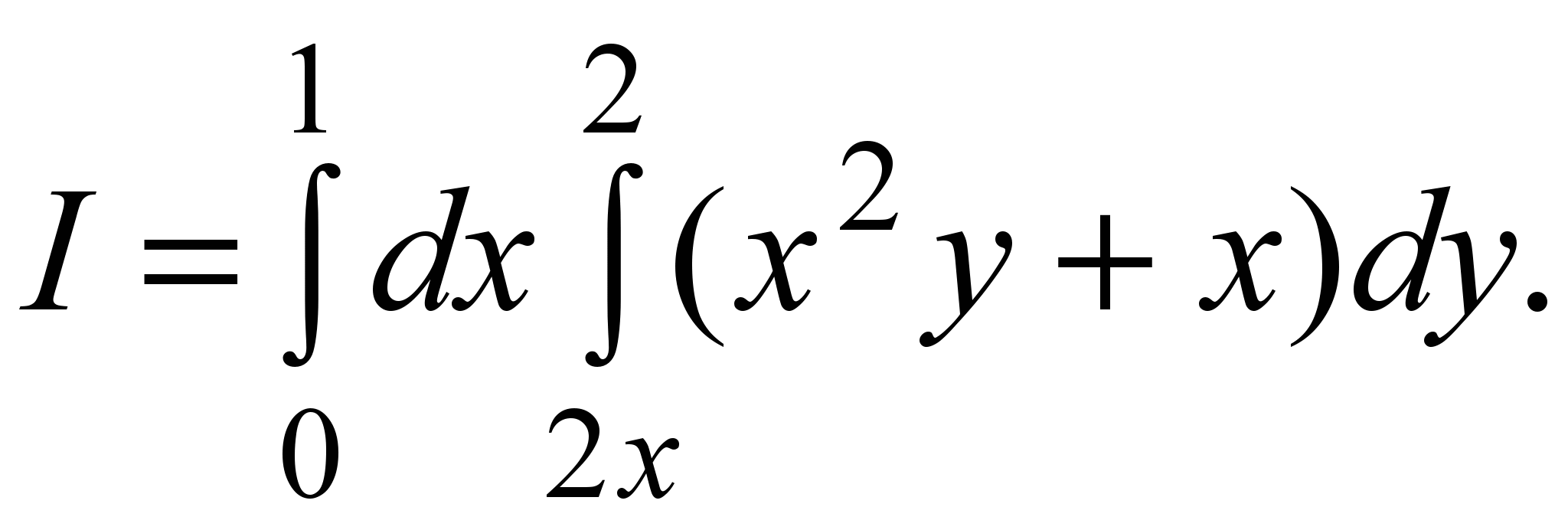
Вычислим внутренний интеграл по переменной y, считая x константой:
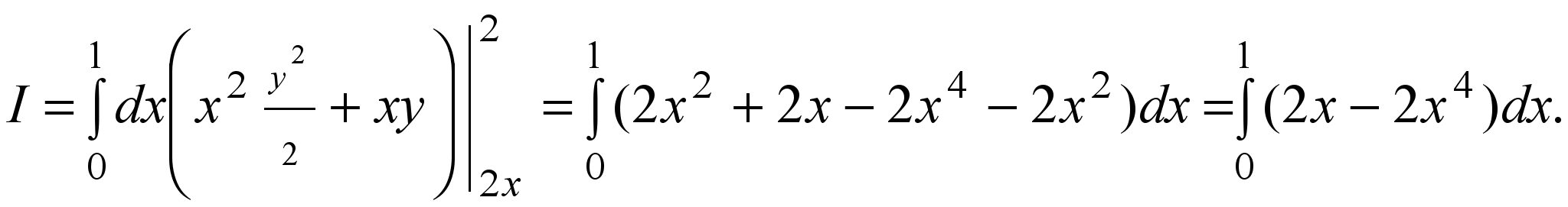
Теперь вычислим внешний интеграл по x:
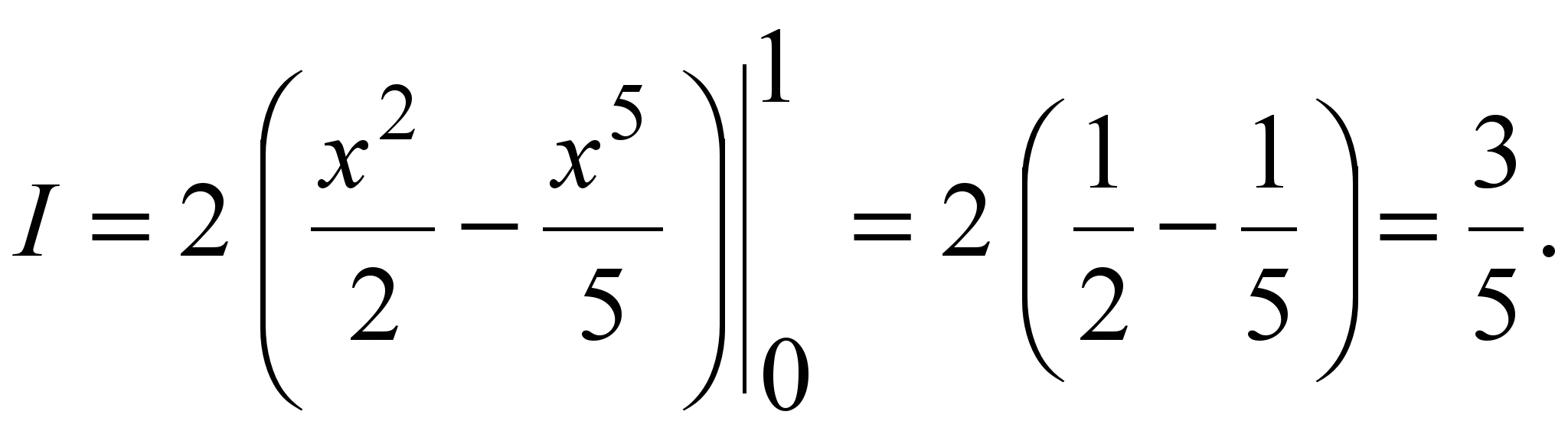
Замена переменных в двойном интеграле.
Иногда для упрощения вычислений делают замену переменных:
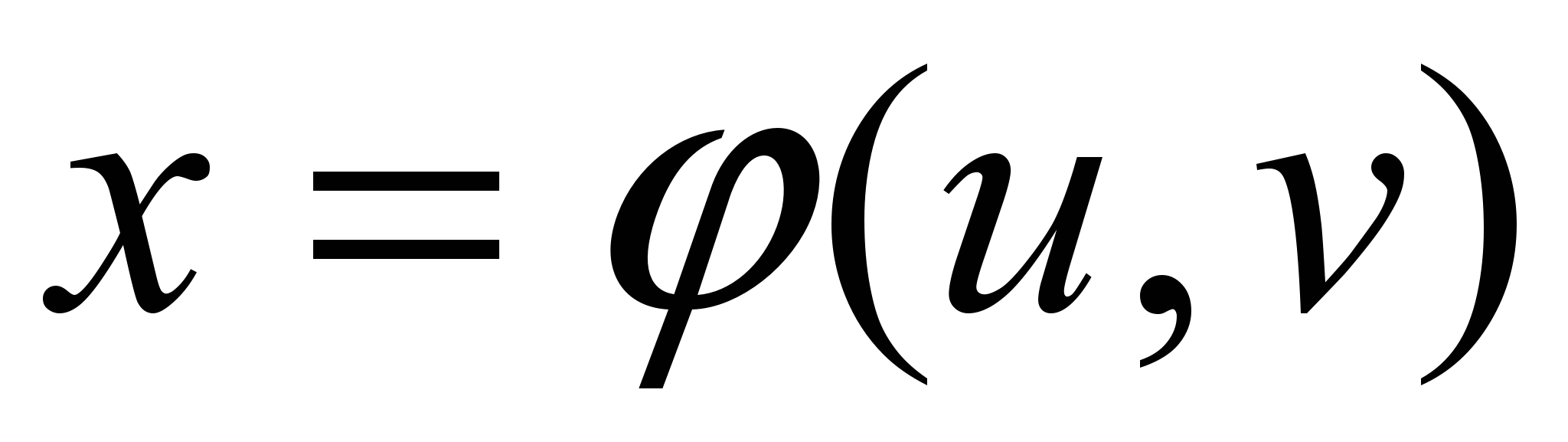 , , 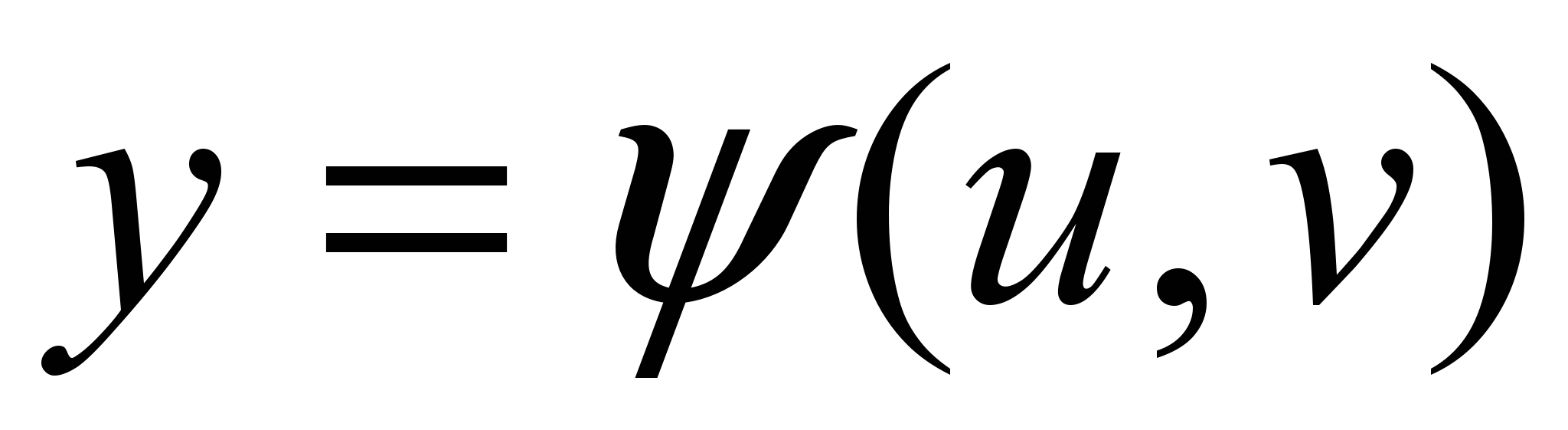 (11) (11)
Если функции (11) непрерывно дифференцируемы и определитель (Якобиан) отличен от нуля в рассматриваемой области:
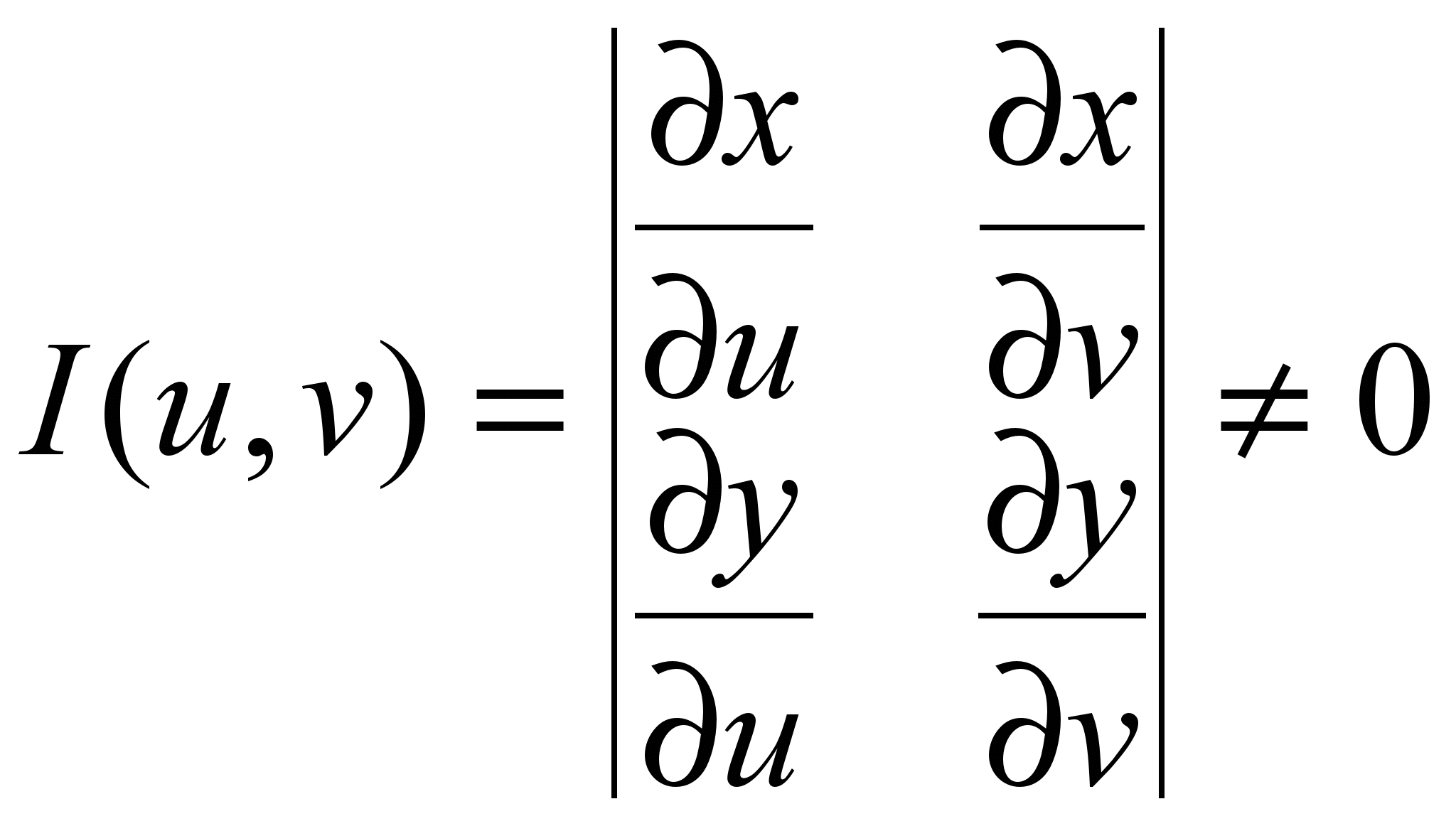 (12) (12)
то: 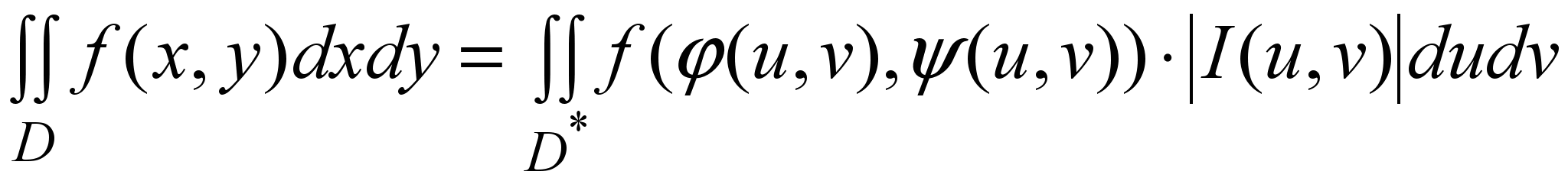 (13) (13)
Двойной интеграл в полярных координатах
В полярных координатах точка 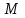 однозначно определяется полярным углом однозначно определяется полярным углом 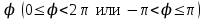 и полярным радиусом и полярным радиусом  . Для начала координат . Для начала координат  радиус радиус 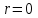 , а полярный угол не определен. , а полярный угол не определен.
Пусть декартовая полуось 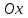 совпадает с полярным лучом .Декартовые координаты выражаются через полярные по формулам совпадает с полярным лучом .Декартовые координаты выражаются через полярные по формулам 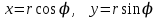 . .
Полярные координаты выражаются через декартовые
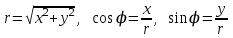 . .

Пусть область D в декартовых координатах преобразуется в область Dr в полярных координатах согласно формулам (10).
Якобиан в данном случае равен:
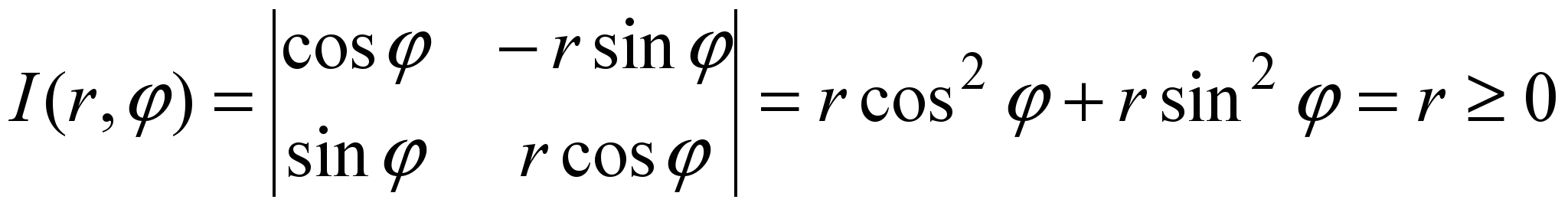
Тогда интеграл (2) преобразуется в двойной интеграл в полярных координатах по формуле
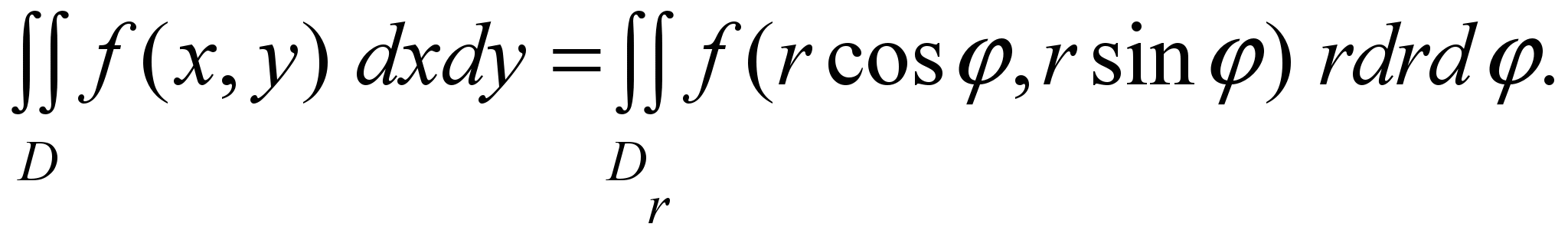 (16) (16)
Двойной интеграл (16) вычисляется переходом к повторному интегралу в полярных координатах. Пусть область Dr имеет вид
Dr= { (r, φ) : α ≤φ≤ β, r1(φ)≤ r≤ r2 (φ)},
где лучи φ= α и φ= β ограничивают сектор, в котором находится фигура Dr , кривые r = r1(φ), r = r2 (φ) ограничивают ее в этом секторе. Тогда
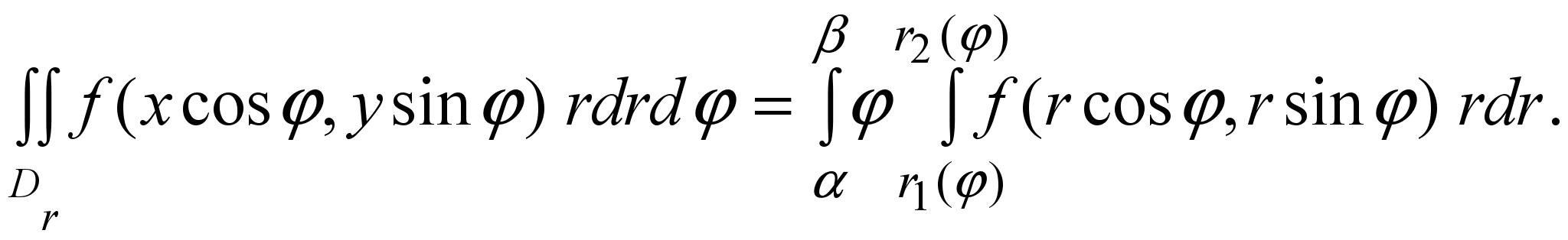 (17) (17)
Замечание. При расстановке пределов интегрирования в повторном интеграле нужно учесть, что изменение полярного угла определяется поворотом луча, исходящего из начала O вокруг него против хода часовой стрелки, а изменение полярного радиуса определяется движением точки вдоль луча в сторону его возрастания.
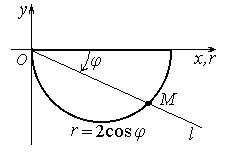
Рисунок 5
Примеры. 1). Расставить пределы интегрирования в повторном интеграле в полярных координатах
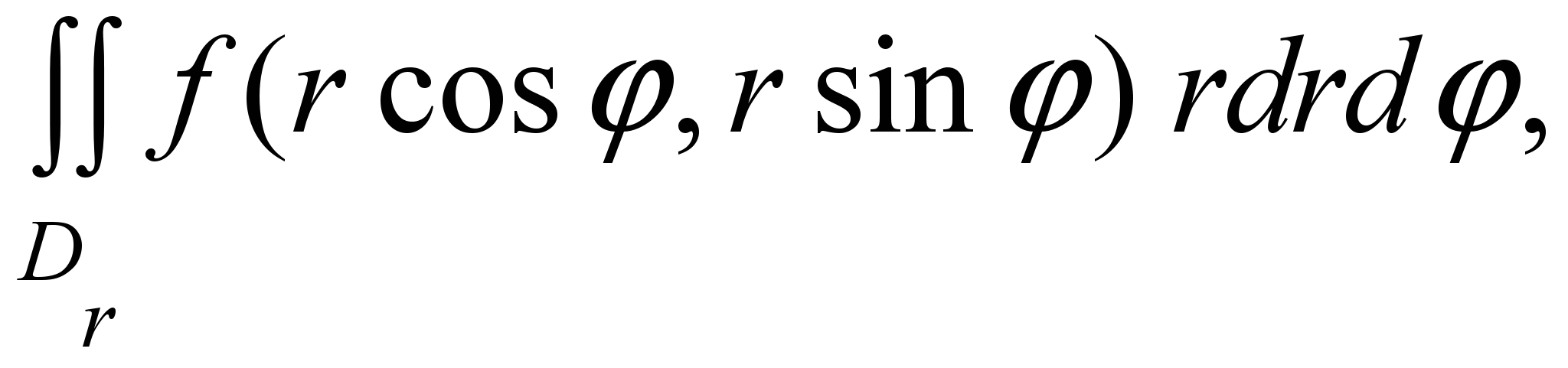
где Dr полукруг из рисунка 5.
Решение. Все точки этого полукруга будут охвачены, если луч Оl будет поворачиваться от 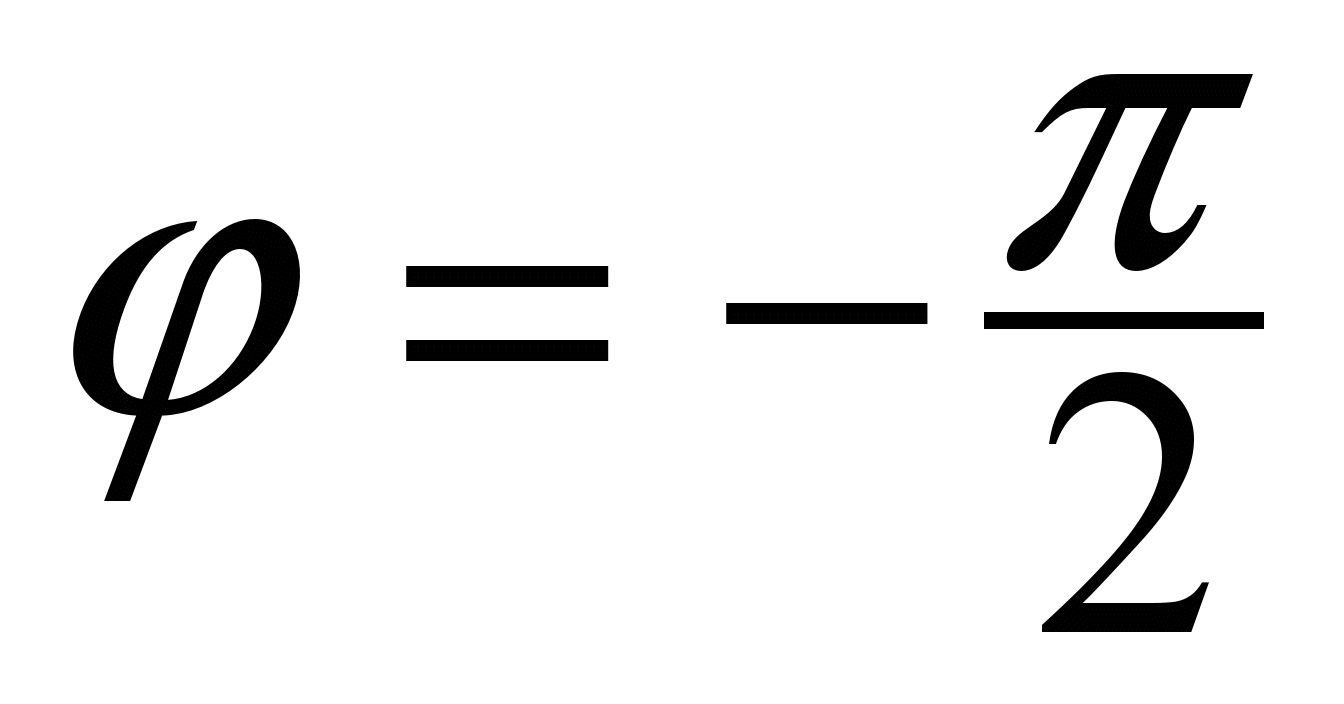 до φ = 0 против хода часовой стрелки. Значит, до φ = 0 против хода часовой стрелки. Значит, 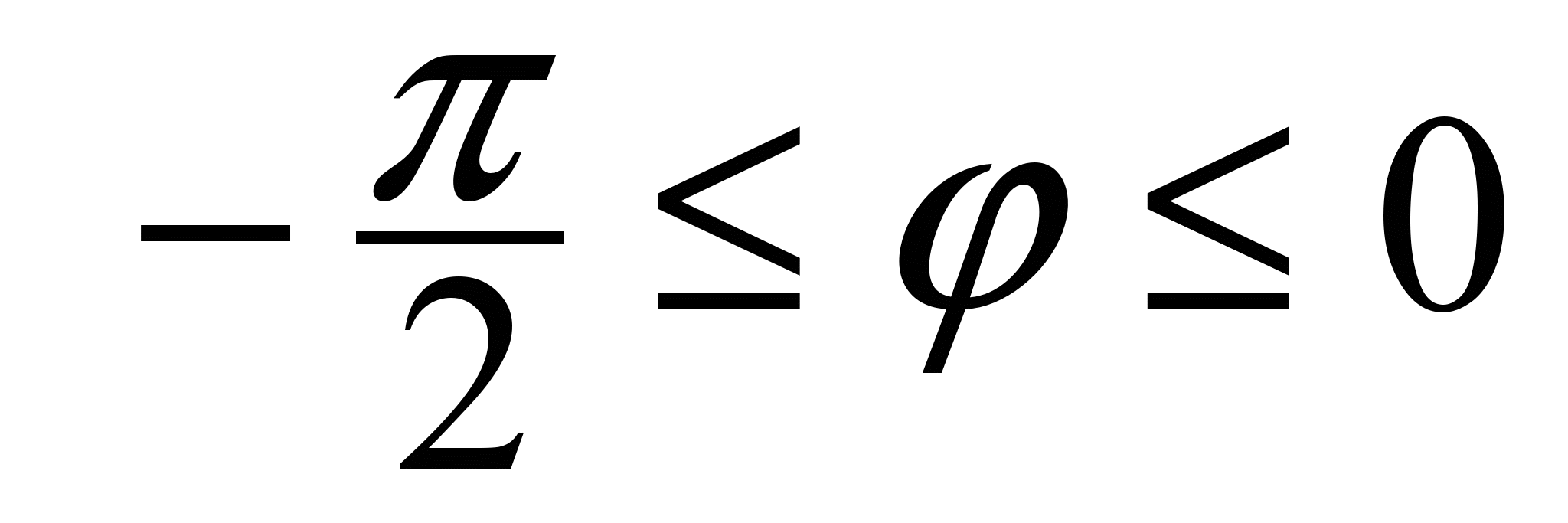 . Пусть теперь луч Оl имеет полярный угол . Пусть теперь луч Оl имеет полярный угол 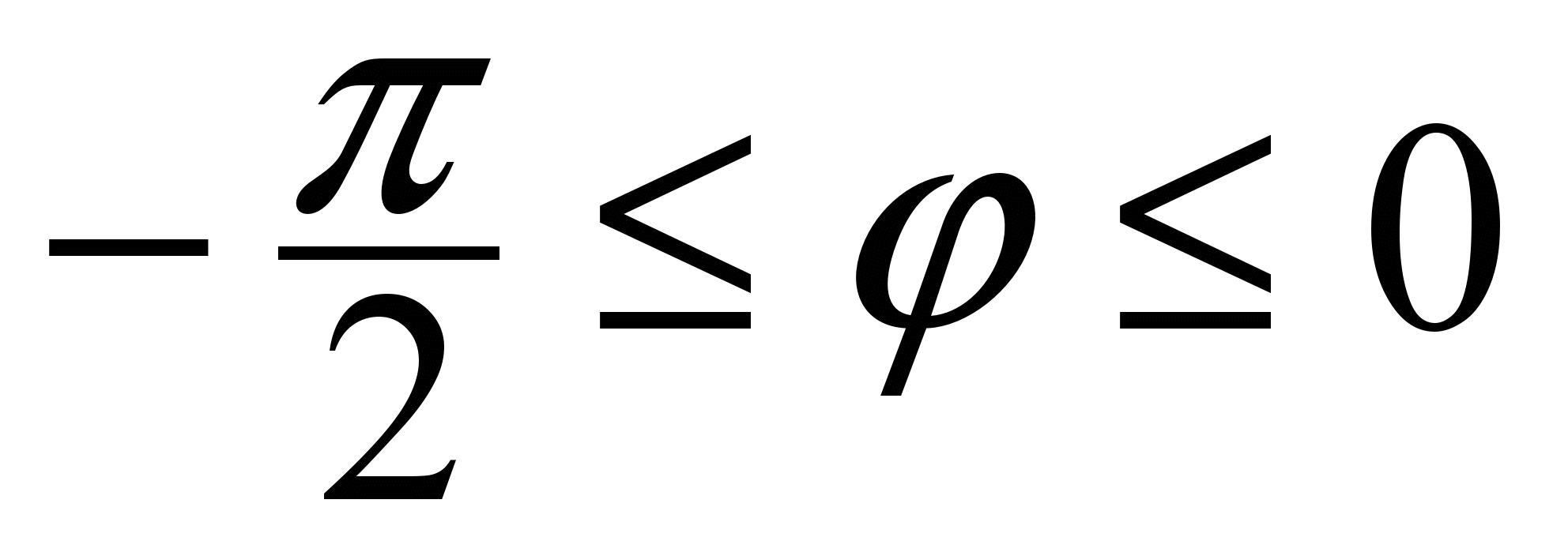 . Тогда при движении точки полукруга по лучу Оl (рис. 5) от точки О до точки Mполярный радиус rизменяется от 0 до координаты r=2cosφ точки M. Значит, . Тогда при движении точки полукруга по лучу Оl (рис. 5) от точки О до точки Mполярный радиус rизменяется от 0 до координаты r=2cosφ точки M. Значит,
0 ≤ r ≤ 2cos φ. Таким образом, Dr ={(r, φ): 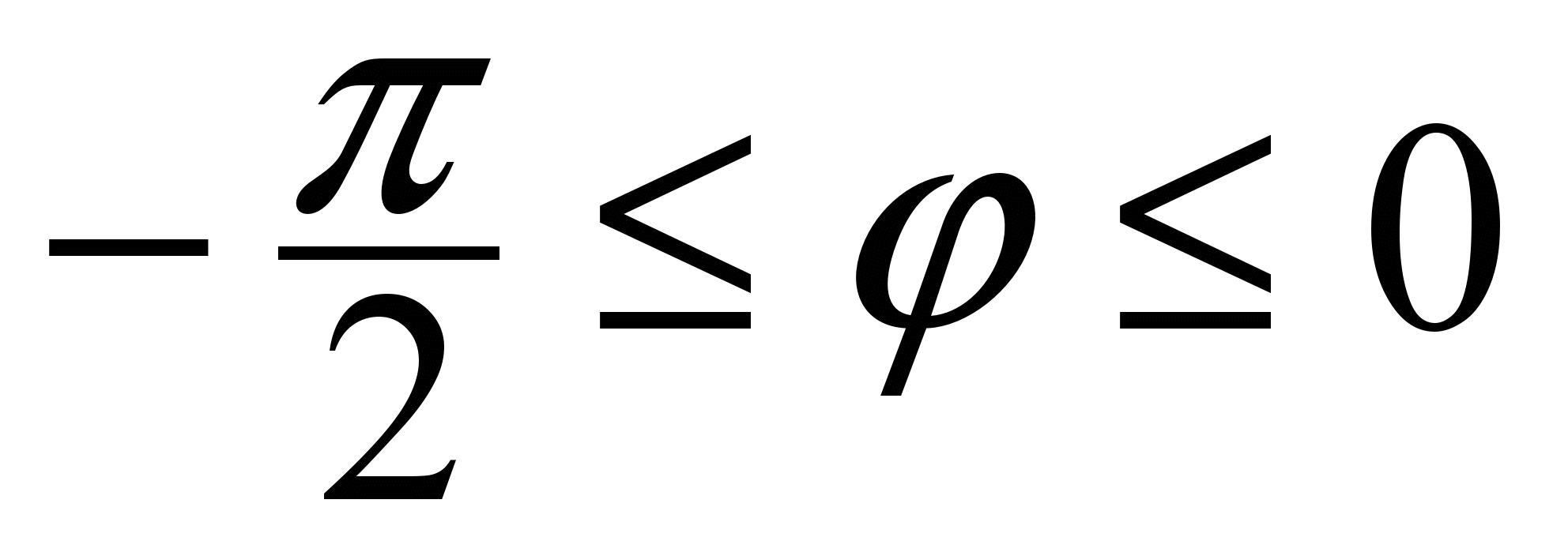 , 0 ≤ r ≤ 2 cos φ}. Следовательно, , 0 ≤ r ≤ 2 cos φ}. Следовательно,
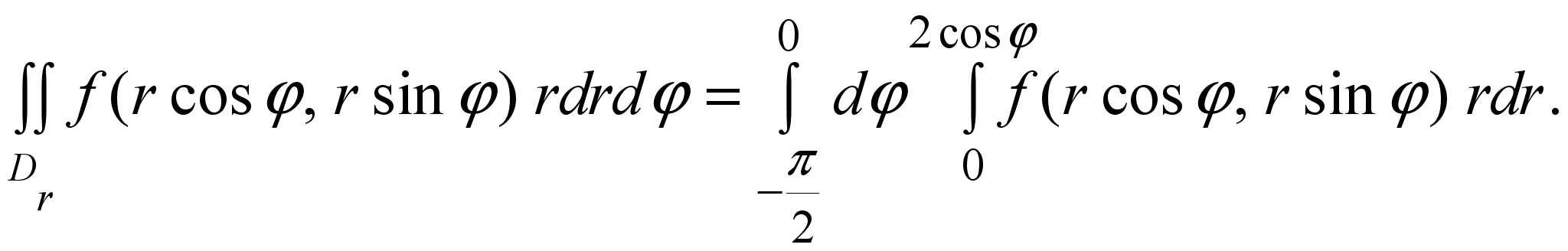
2) Вычислить 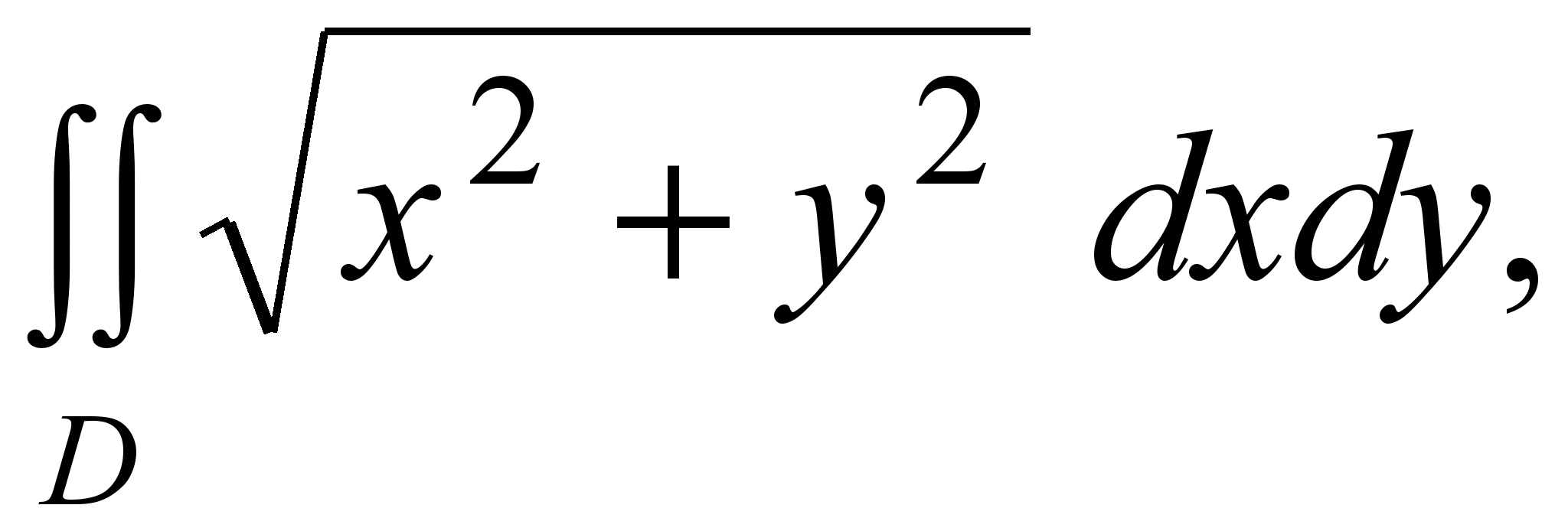 где D ={(x, y): x2+ y22x ≤0, y≤0}. где D ={(x, y): x2+ y22x ≤0, y≤0}.
Решение. Подставим в уравнение окружности x2+y22x =0 полярные координаты (9) и преобразуем: r22 rcosφ= 0  r =2cosφ. Мы получили уравнение полуокружности в полярных координатах из рисунка 5. Поскольку y≤0, то D полукруг из примера 3. Расставим пределы интегрирования как в этом примере и вычислим: r =2cosφ. Мы получили уравнение полуокружности в полярных координатах из рисунка 5. Поскольку y≤0, то D полукруг из примера 3. Расставим пределы интегрирования как в этом примере и вычислим:
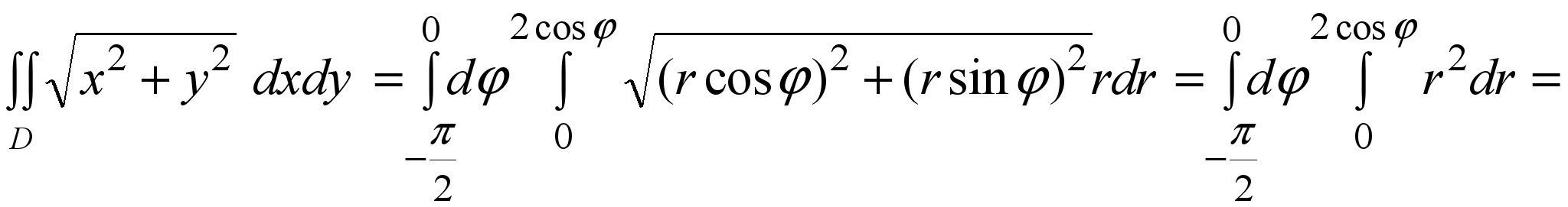
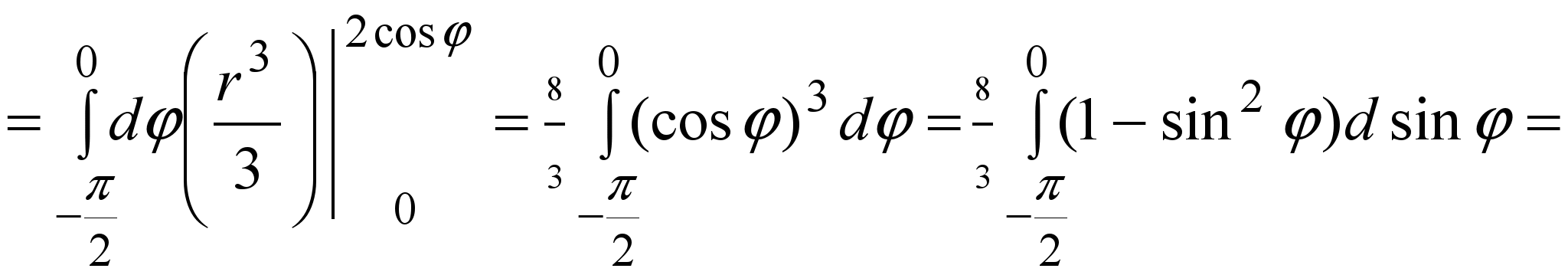
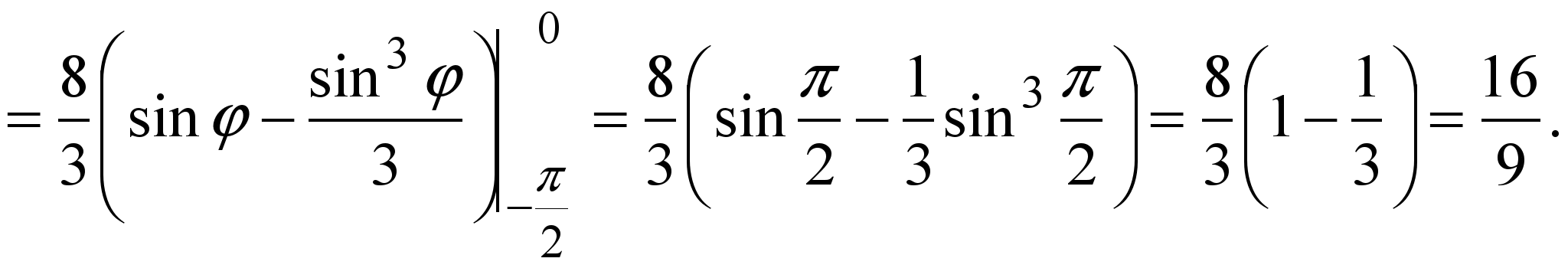
Вычисление площади фигуры.
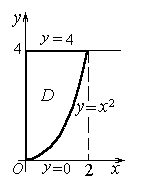
Площадь плоской фигуры вычисляется по формуле 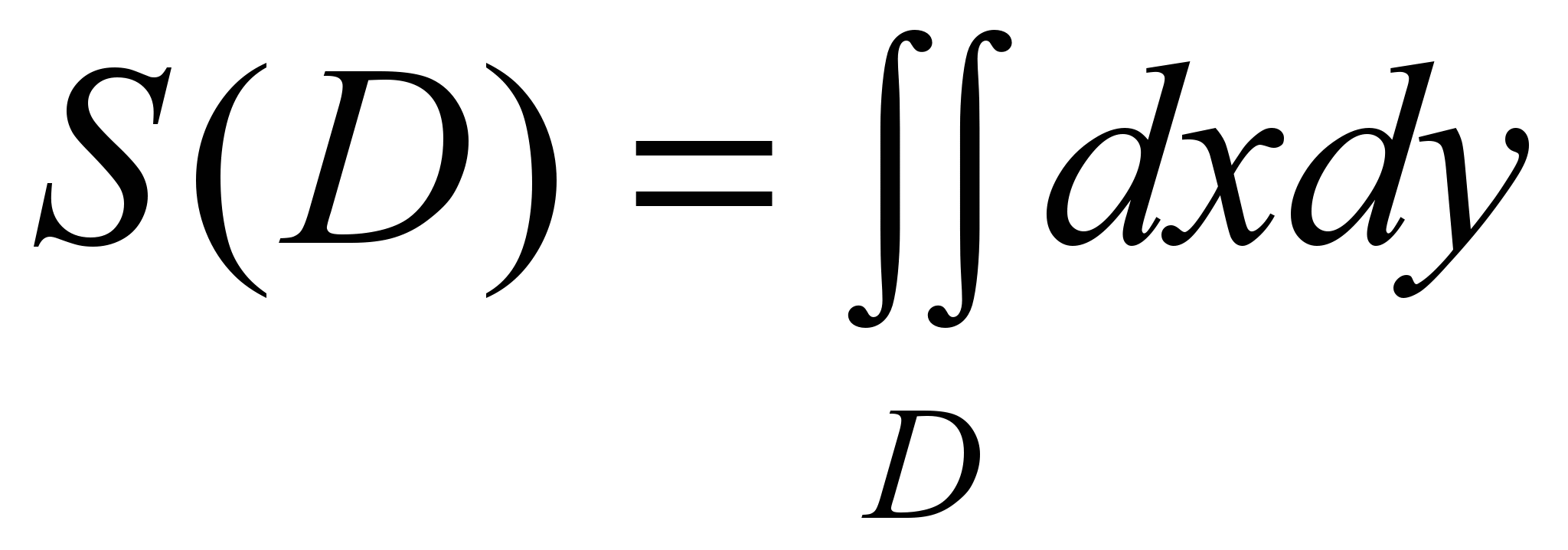
Пример. Вычислить площадь фигуры, ограниченной линиями 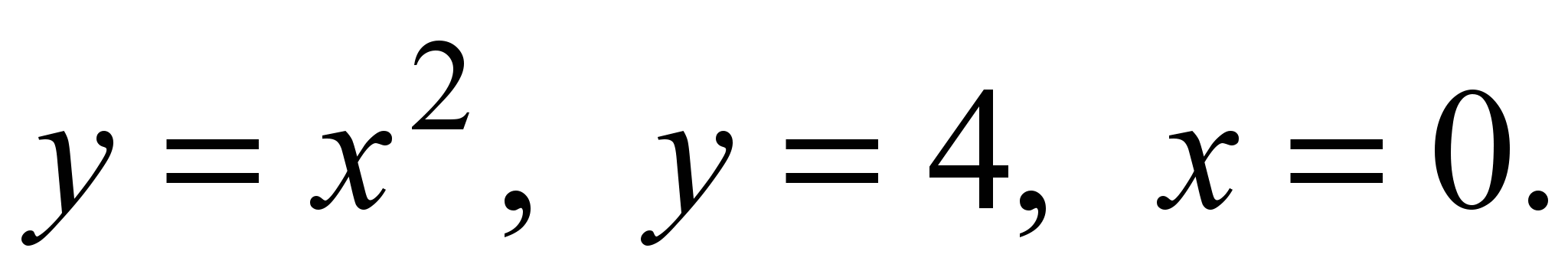
Решение. Данная фигура D расположена в вертикальной полосе 0 ≤ x ≤ 2, а в ней ограничена снизу параболой y = x2, сверху прямой y =4 (рис. 6). По формуле (5) имеем
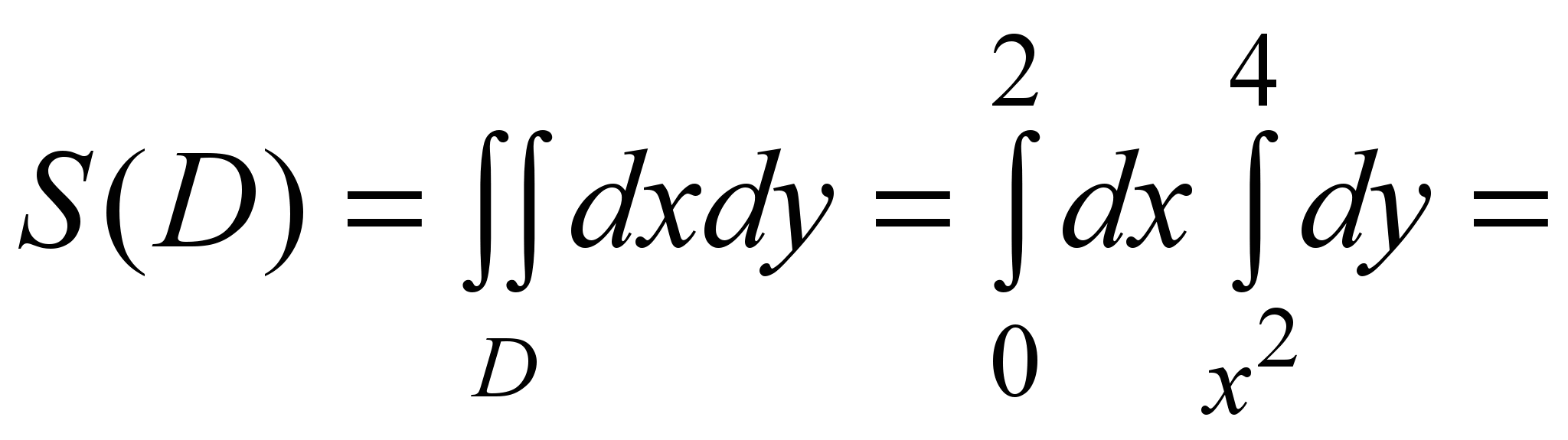 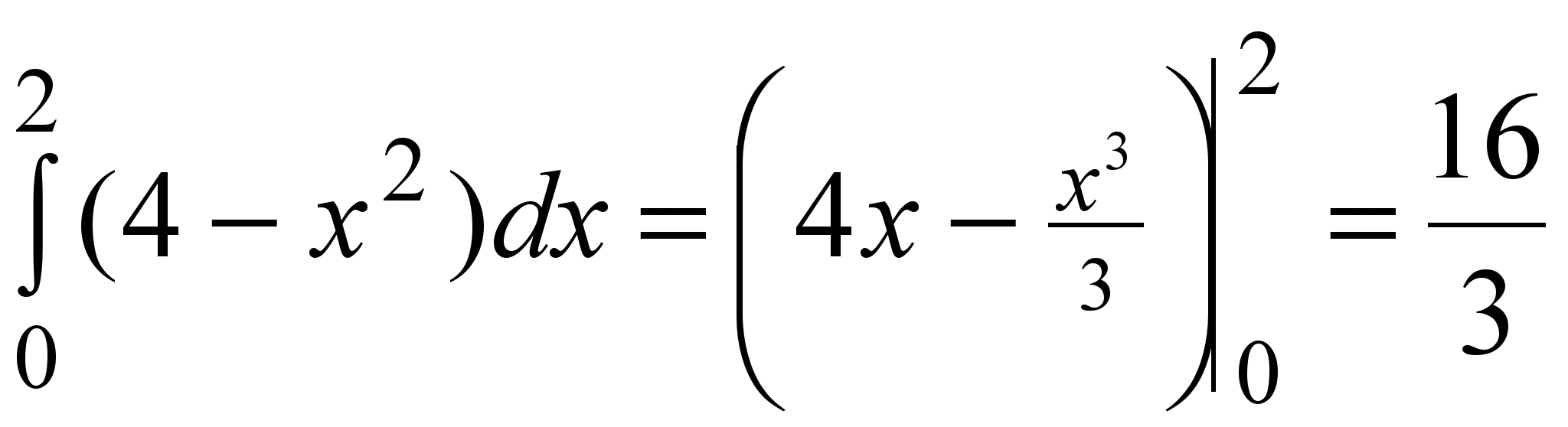 . .
Вычисление объема цилиндрического тела.
Если f (x,y) ≥ 0 в ограниченной области D, то объем цилиндрического тела (рис.1) вычисляется по формуле V = 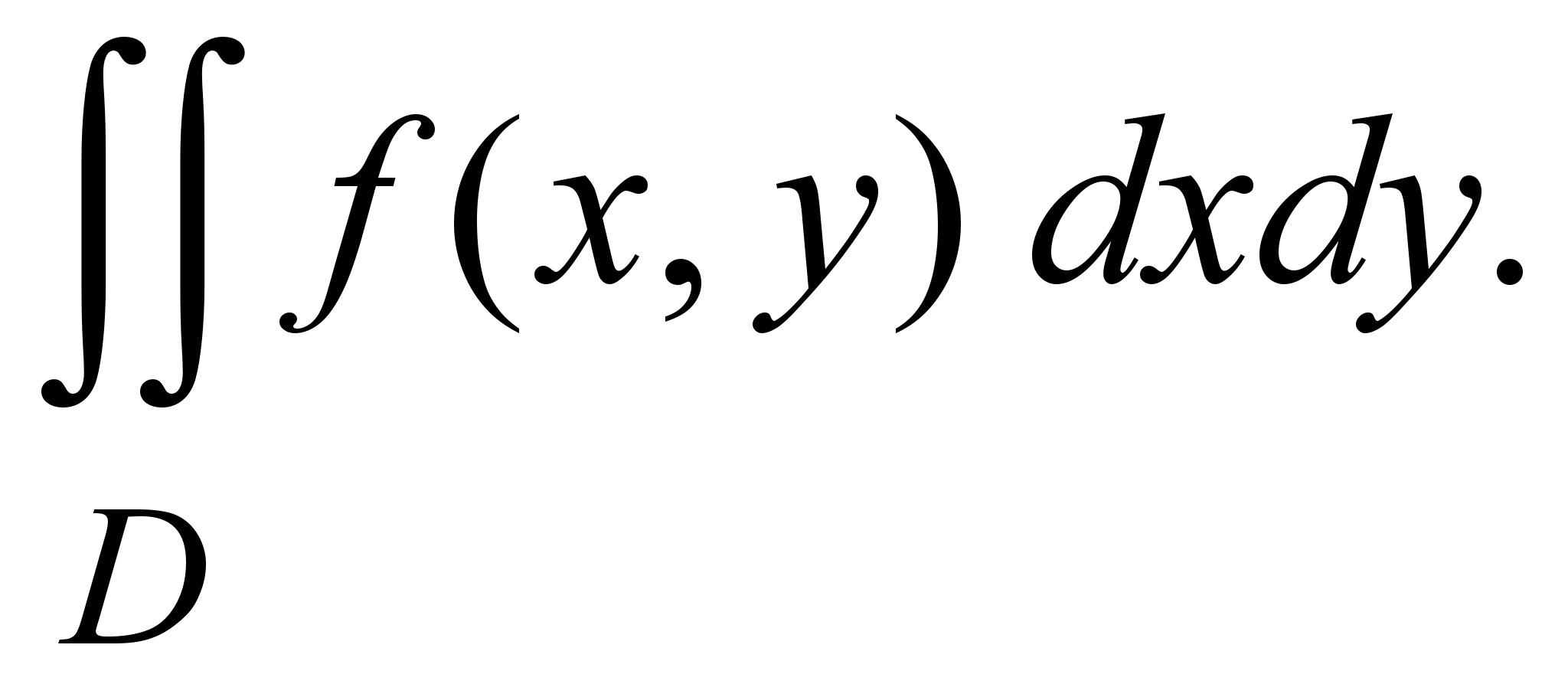
Пример. Найти объем тела, ограниченного поверхностями
z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. x2 + y2 = 4 это круговой цилиндр радиуса 2, ось которого совпадает с Оy. z = x2 + y2 параболоид, который пересекает цилиндр по окружности радиуса 2 в плоскости z = 4 . z=0 координатная плоскость xOy. Таким образом, тело ограничено сверху параболоидом
z = x2 + y2 , снизу кругом D , с боков цилиндрической поверхностью x2 + y2 = 4. Так как данное тело цилиндрическое и
z = x2 + y2 ≥ 0, то для вычисления его объема можно использовать формулу

где D ={ (x, y) : x2 + y2 ≤ 4, z = 0}круг в плоскости xOy. Для вычисления этого интеграла перейдем к полярным координатам. При этом круг Dпреобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }. По формуле (17) получим

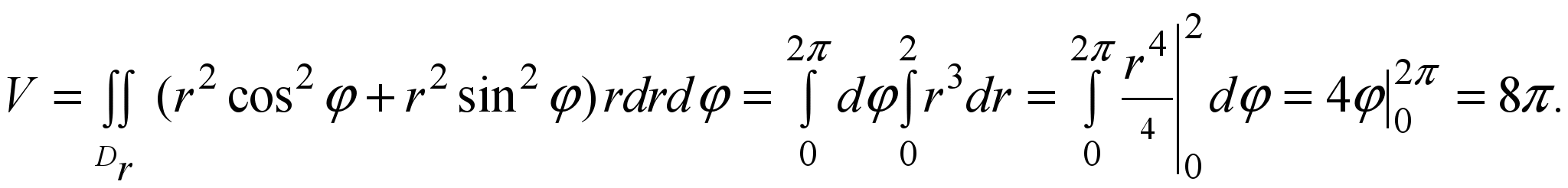 
Занятие 27. Тема «Двойной интеграл и его свойства. Приложение двойного интеграла»
План лекции:
Понятие двойного интеграла
Свойства двойного интеграла
Правила вычисления двойного интеграла
Понятие двойного интеграла
Определение: Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функции двух переменных. В этом случае вместо отрезка интегрирования будет присутствовать какая-то плоская фигура.
Двойной интеграл в общем виде записывается следующим образом:
, где – знак двойного интеграла;
D – область интегрирования (плоская фигура);
f(x;y) – подынтегральная функция двух переменных;
dx, dy – элементы площади интегрирования.
Пусть D – некоторая замкнутая ограниченная область, а f(x,y) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y=f(x) или x=g(y), где f(x) и g(y) – непрерывные функции.
Свойства двойного интеграла
Если С – числовая константа, то ,
Если область D “разбита” на области D1 и D2, то
.
Правила вычисления двойного интеграла
Чтобы вычислить двойной интеграл, нужно для начала построить область D в системе координат и определить границы этой области по оси Ох и по оси Оу. Затем выбрать один из видов области интегрирования по правилу 2, подставить в функцию и вычислить двойной интеграл по 3 правилу.
Различают два основных вида области интегрирования.
Область интегрирования D ограничена слева и справа прямыми х=а и х=b (ab), а снизу и сверху – непрерывными кривыми y= и y= ( ).
Для такой области интеграл вычисляется следующим образом
Область интегрирования D ограничена снизу и сверху прямыми у=с и y=d (cd), а слева и справа – непрерывными кривыми x= и y= ( )
Для такой области интеграл вычисляется следующим образом
При вычислении двойного интеграла сначала вычисляется внутренний интеграл, используя формулу Ньютона-Лейбница, считая одну из переменных постоянным числом:
здесь х считается постоянным числом.
здесь у считается постоянным числом.
Затем, вычисляется внешний интеграл также по формуле Ньютона-Лейбница.
Пример1. Вычислить двойной интеграл , где
Решение. 1. Строим область интегрирования D
2 . Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования .
Вычисляем внутренний (правый) интеграл, считая у - числом, которое можно вынести за знак интеграла. Получаем .
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл ,
где .
Решение. 1. Строим область интегрирования D
2. Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования
Вычисляем внутренний (правый) интеграл, считая х - число. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Ответить на контрольные вопросы:
Что называется двойным интегралом?
Перечислите основные свойства двойного интеграла.
На какие виды делится область интегрирования?
Каким образом вычисляется двойной интеграл?
Что делать с переменной, если она в интеграле не является интегрируемой?
Пользуясь учебником П.Е. Данко «Высшая математика в упражнениях и задачах» часть 2, разобрать №4 стр.8 рис.3, выписать в тетрадь.
Тройной интеграл.
Контрольные вопросы.
Тройной интеграл, его свойства.
Вычисление тройного интеграла в декартовых координатах.
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
Вычисление тройного интеграла в сферических координатах.
Пусть функция u = f(x,y,z) определена в ограниченной замкнутой области V пространства R3. Разобьём область V произвольным образом наn элементарных замкнутых областей V1, … , Vn, имеющих объемы V1, …,Vn соответственно. Обозначим d – наибольший из диаметров областей V1, … , Vn. В каждой области Vk выберем произвольную точку Pk (xk , yk , zk) и составим интегральную сумму функции f(x, y, z)
S =
Определение. Тройным интегралом от функции f(x, y, z) по области V называется предел интегральной суммы , если он существует.
Таким образом,
(1)
Замечание. Интегральная сумма S зависит от способа разбиения области Vи выбора точек Pk (k=1, …, n). Однако, если существует предел, то он не зависит от способа разбиения области V и выбора точек Pk . Если сравнить определения двойного и тройного интегралов, то легко увидеть в них полную аналогию.
Достаточное условие существования тройного интеграла. Тройной интеграл (13) существует, если функция f(x, y, z) ограничена в V и непрерывна в V, за исключением конечного числа кусочно-гладких поверхностей, расположенных в V .
В дальнейшем будем считать, что все рассматриваемые тройные интегралы существуют.
Некоторые свойства тройного интеграла.
1) Если С – числовая константа, то
3) Аддитивность по области. Если область Vразбита на области V1и V2, то
.
4) Объем тела V равен
(2)
Вычисление тройного интеграла в декартовых координатах.
Пусть D проекция тела V на плоскость xOy, поверхности z=φ1(x, y), z=φ2(x, y) ограничивают тело V снизу и сверху соответственно. Это значит, что
V = {(x, y, z): (x, y)D, φ1(x, y) ≤ z ≤ φ2(x, y)}.
Такое тело назовем z-цилиндрическим. Тройной интеграл (1) по z-цилиндрическому телу V вычисляется переходом к повторному интегралу, состоящему из двойного и определенного интегралов:
(3)
В этом повторном интеграле сначала вычисляется внутренний определенный интеграл по переменной z, при этом x, y считаются постоянными. Затем вычисляется двойной интеграл от полученной функции по области D.
Если V x-цилиндрическое или y-цилиндрическое тело, то верны соответственно формулы
В первой формуле D проекция тела V на координатную плоскость yOz, а во второй на плоскость xOz
Примеры. 1) Вычислить объем тела V, ограниченного поверхностями z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. Вычислим объём при помощи тройного интеграла по формуле (2)
Перейдем к повторному интегралу по формуле (3).
Пусть D круг x2 + y2 ≤ 4, φ1(x, y)= 0, φ2(x, y)= x2 + y2 . Тогда по формуле (3) получим
Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }.
2) Тело Vограничено поверхностями z=y, z= –y, x=0, x=2, y=1. Вычислить
Плоскости z = y, z = –y ограничивают тело соответственно снизу и сверху, плоскости x=0, x=2 ограничивают тело соответственно сзади и спереди, а плоскость y=1 ограничивает справа. V – z-цилиндрическое тело, его проекцией D на плоскость хОу является прямоугольник ОАВС. Положим φ1(x, y)= –y, φ2(x, y)= y и применим формулу (3):
|
 Скачать 1.34 Mb.
Скачать 1.34 Mb.
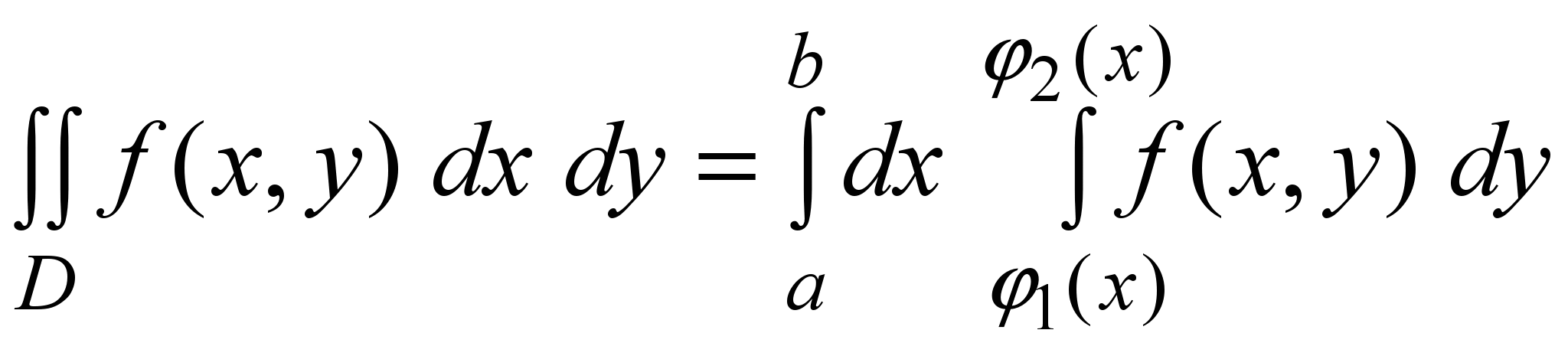 (7)
(7)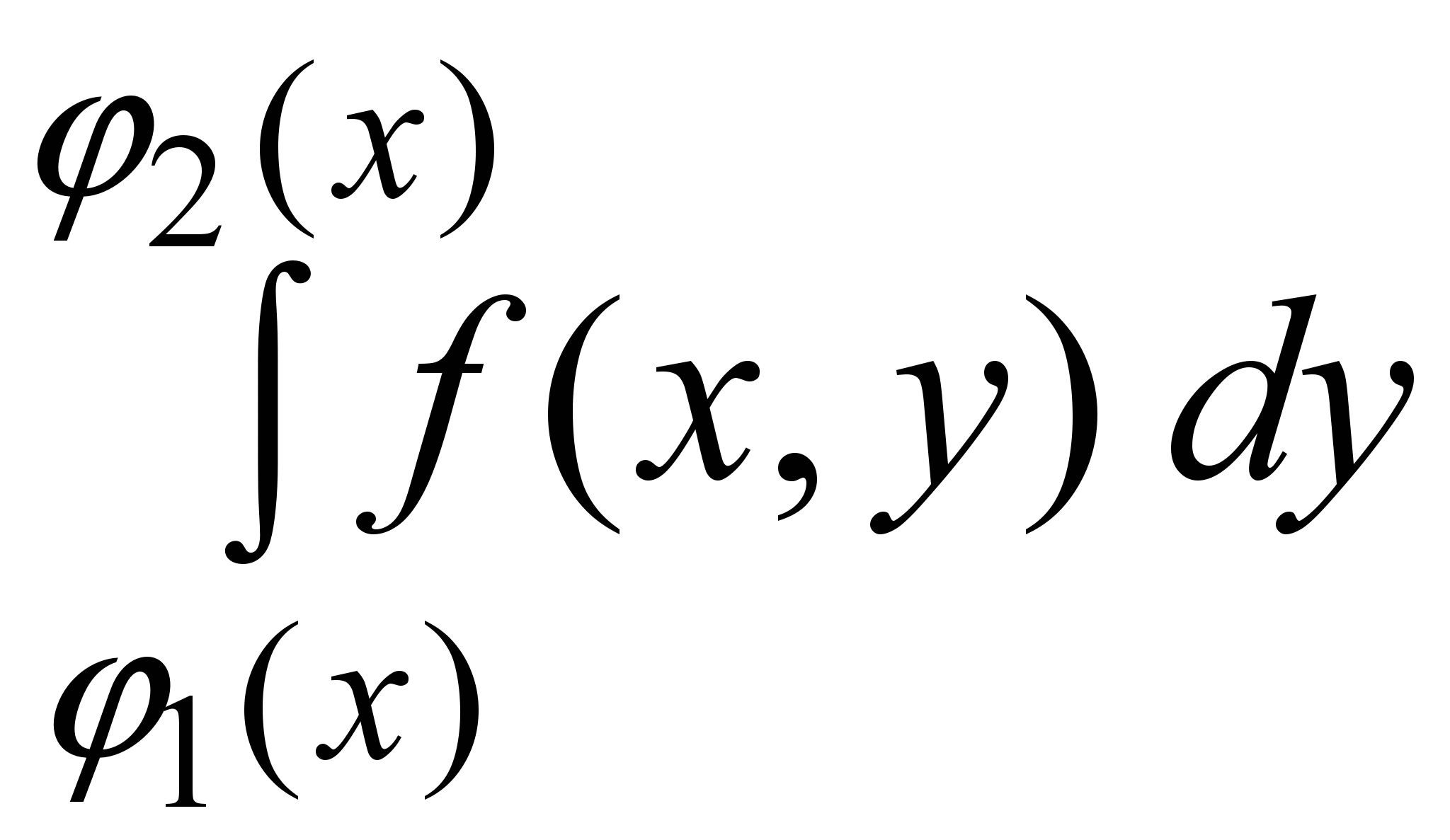
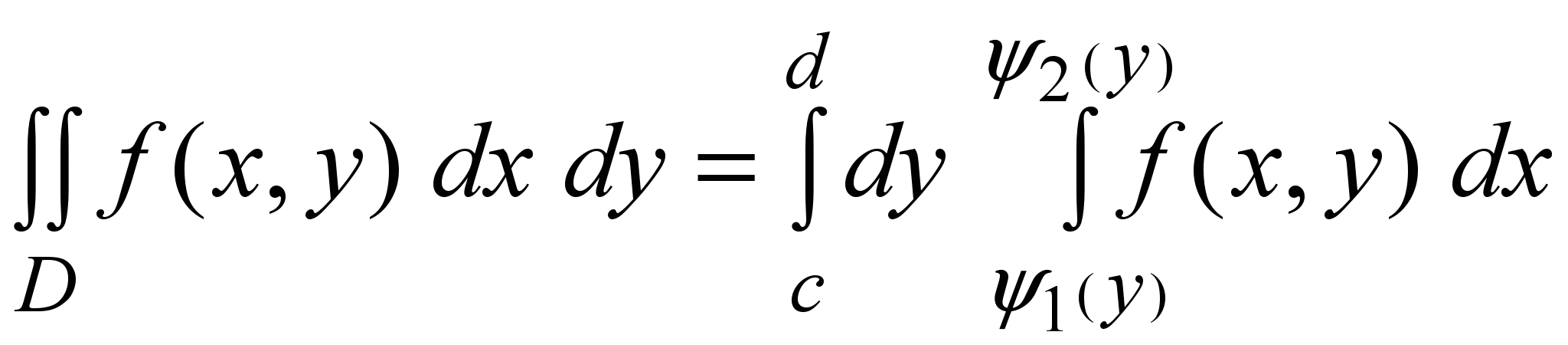 . (9)
. (9)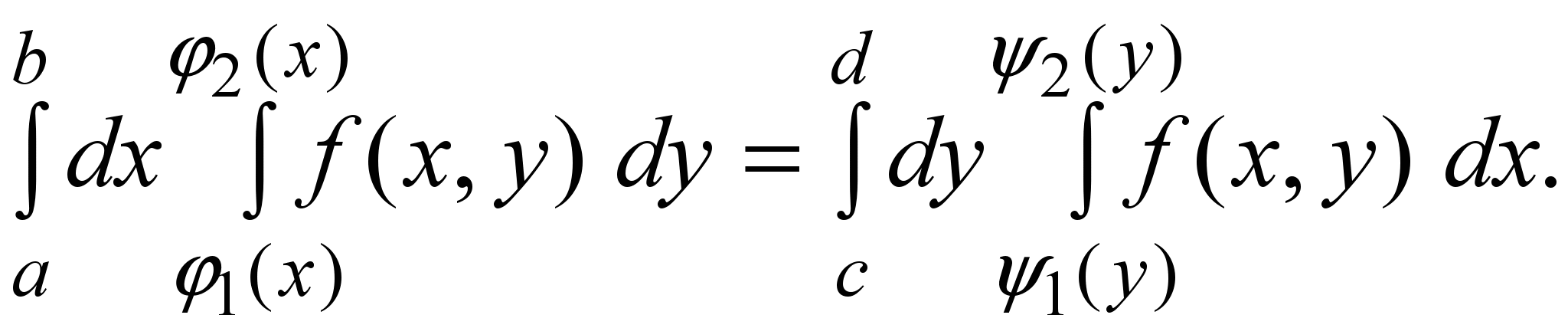 (10)
(10)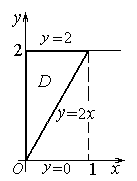
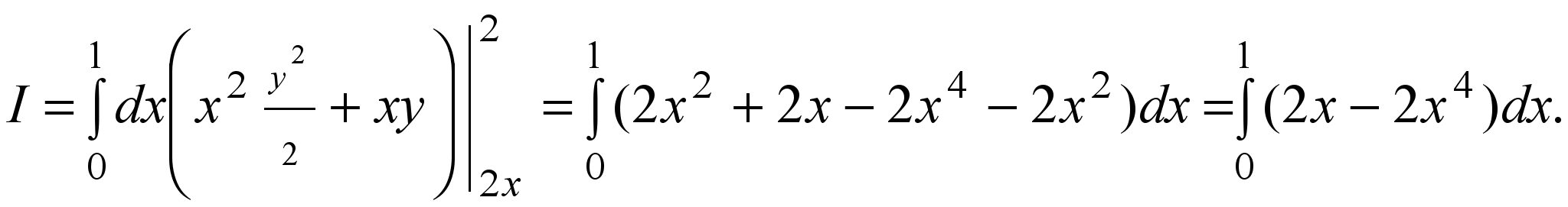
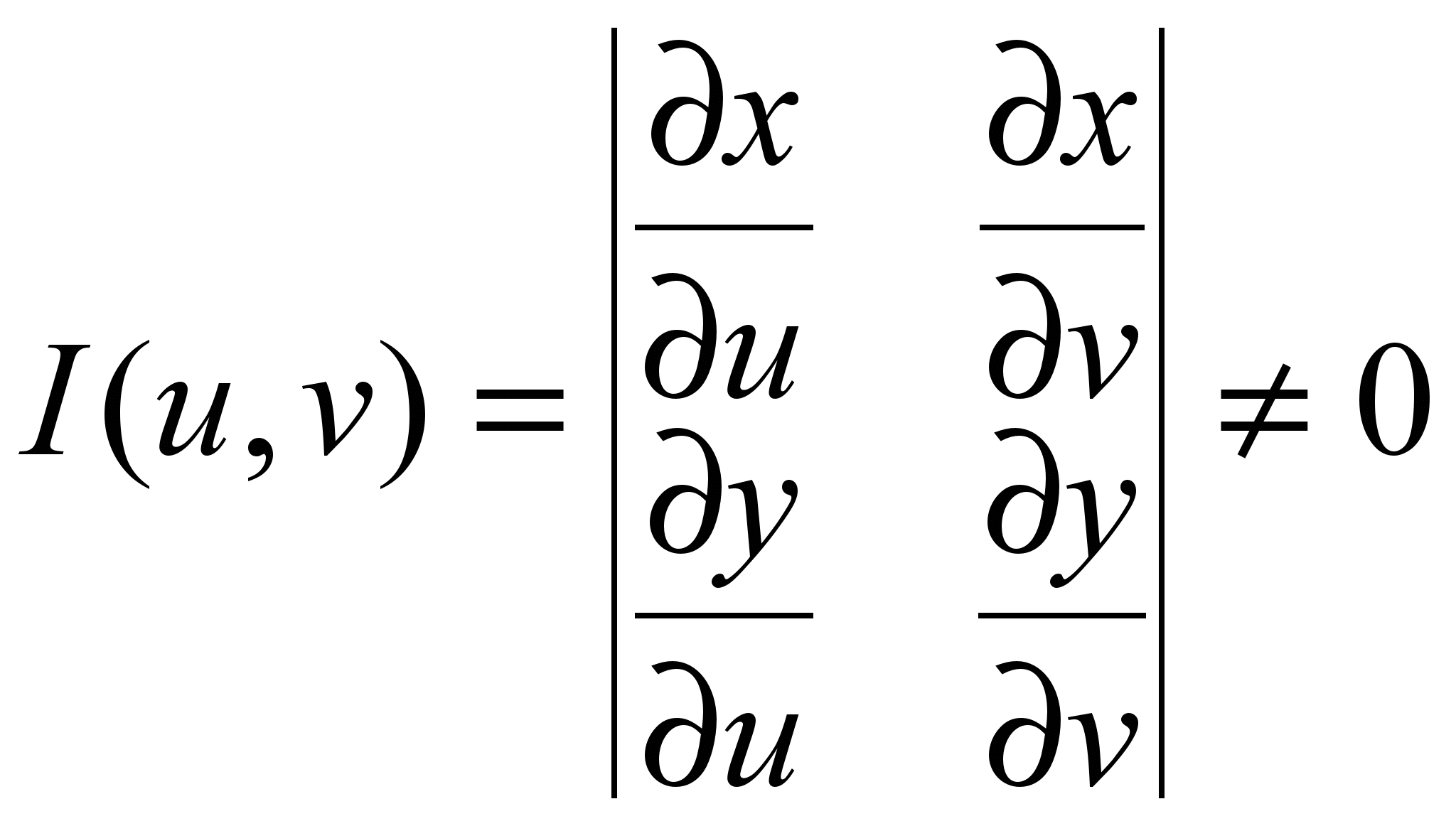 (12)
(12)
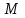 однозначно определяется полярным углом
однозначно определяется полярным углом 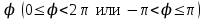 и полярным радиусом
и полярным радиусом  . Для начала координат
. Для начала координат  радиус
радиус 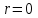 , а полярный угол не определен.
, а полярный угол не определен.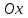 совпадает с полярным лучом .Декартовые координаты выражаются через полярные по формулам
совпадает с полярным лучом .Декартовые координаты выражаются через полярные по формулам 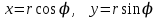 .
.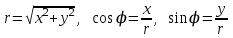 .
.
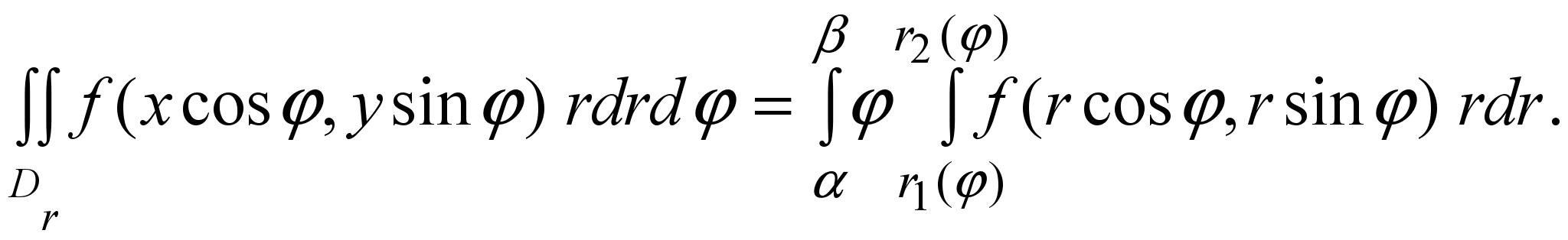 (17)
(17)
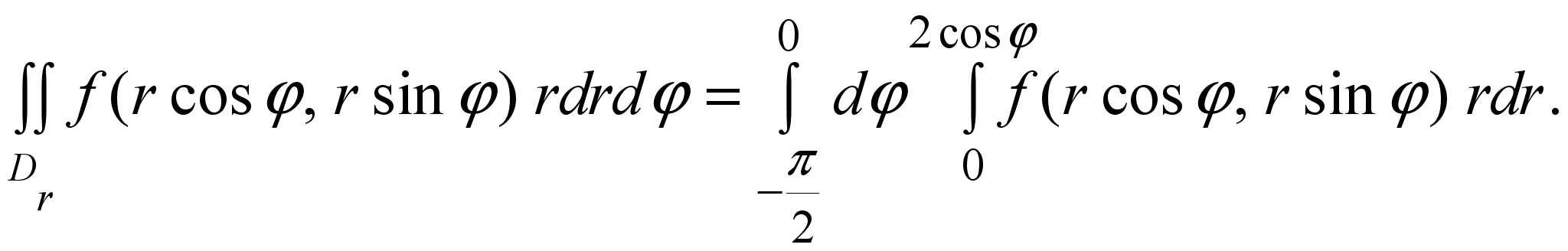
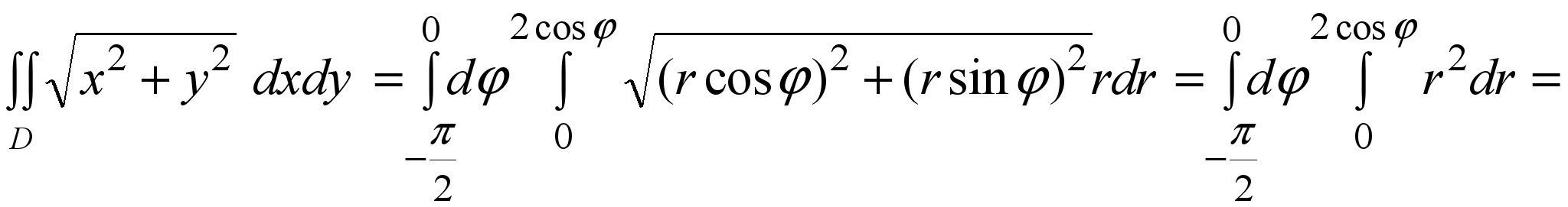
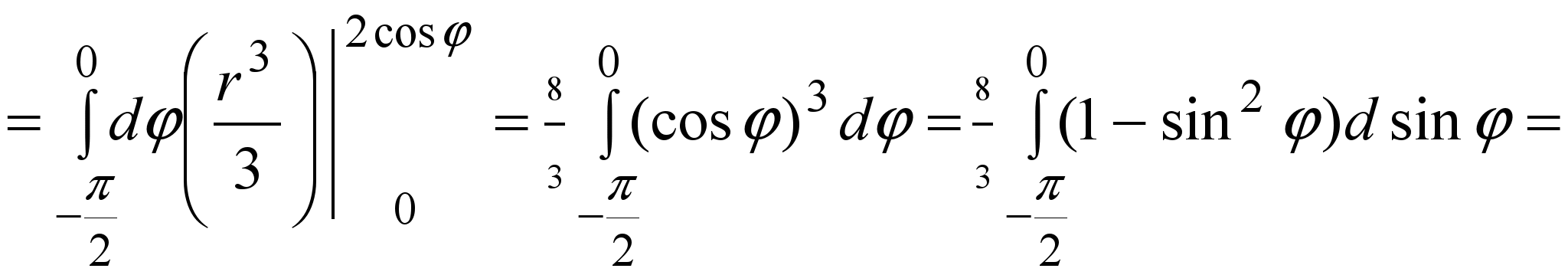
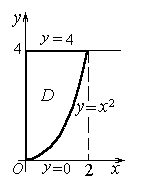
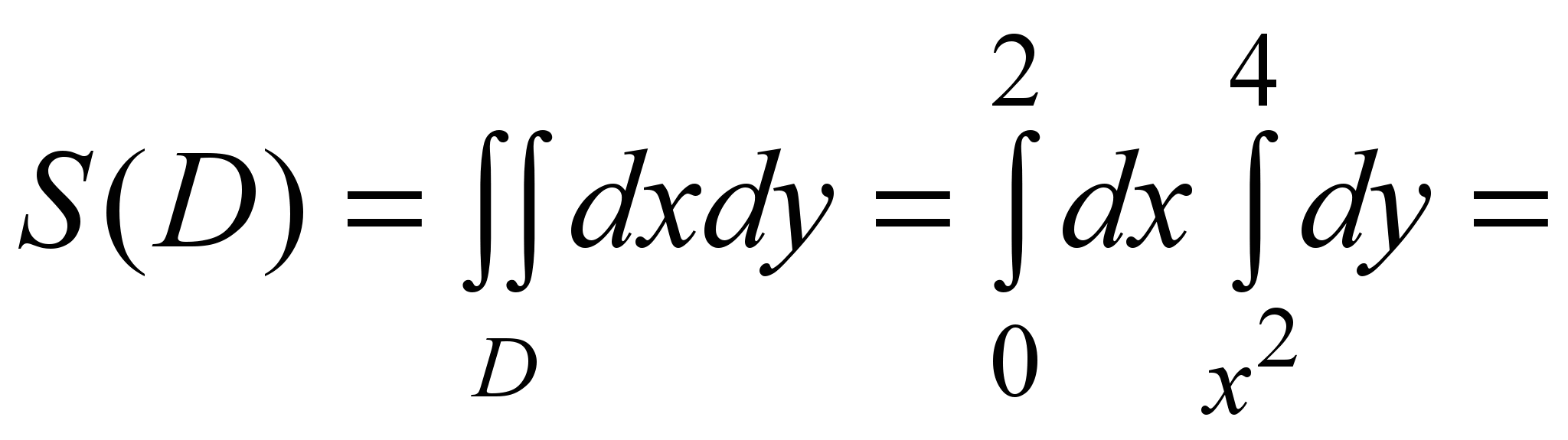
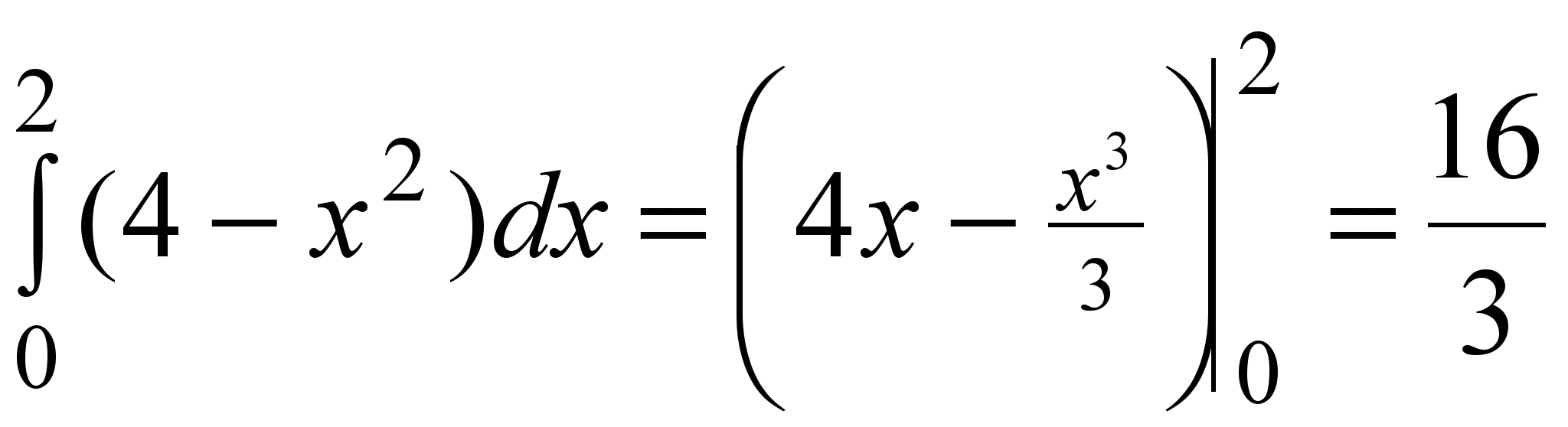 .
.