экзамен по биометрии. билеты. Понятие о биометрии. Биометрия
 Скачать 39.55 Kb. Скачать 39.55 Kb.
|
|
Понятие о биометрии. "Биометрия – прикладная наука, использующая математические методы статистического анализа массовых явлений (результатов наблюдений, учетов) применительно к биологическим объектам (растениям, животным и т.п.)". По мере превращения биологии из науки описательной в науку точную, основанную на измерениях, возникла потребность в применении методов математической статистики для решения биологических задач. Биометрия преследует исключительно биологические цели, приспосабливая методы математической статистики к задачам и специфике биологических исследований. История, пути и направления развития статистики и биометрии Биометрия сложилась в XIX веке — главным образом благодаря трудам Фрэнсиса Гальтона и Карла Пирсона. В 1920-х — 1930-х годах крупный вклад в развитие биометрии внес Рональд Фишер. У истоков биометрии стоял Фрэнсис Гальтон (1822—1911). Первоначально Гальтон готовился стать врачом. Однако, обучаясь в Кембриджском университете, он увлекся естествознанием, метеорологией, антропологией, наследственностью и теорией эволюции. В его книге, посвященной природной наследственности, изданной в 1889 году им впервые было введено в употребление слово biometry; в это же время он разработал основы корреляционного анализа. Гальтон заложил основы новой науки и дал ей имя. Биометрия как наука имеет специализированные направления теоретического и прикладного характера. В прикладном аспекте биометрия рассматривается как метод идентификации человека, основанный на его физиологической или поведенческой характеристике. Биометрические технологии идентификации личности, основанные на распознавании человека по внешним морфологическим признакам, имеют глубокие исторические корни. Способность людей узнавать друг друга по внешнему виду, голосу, запаху, походке и т.д. есть не что иное, как элементарная биометрическая идентификация Проблемы развития биометрии Система формирования ЕБС, основанная на сборе и использовании данных только в банковском секторе замедляет развитие биометрии и требует ее распространения на другие сферы деятельности, в т.ч. на предприятия транспорта, госуслуг, торговли и ресторанного бизнеса и т.д.. Изучению этой проблемы в целях разработки рекомендаций по ее решению и посвящена представленная статья. Материалы и методы: Исследование проведено на основе использования методов широкомасштабного сбора данных, бенчмаркинга, анализа и синтеза полученной информации, разработки рекомендаций по решению представленной проблемы, Результаты: В результате проведенного исследования были определены факторы, сдерживающие сбор биометрических данных, включая:- капиталоёмкий процесса сбора данных, требующий значительных затрат на организацию сбора данных, оснащение оборудованием и программным обеспечением, обучение персонала; - отсутствие доверия граждан к этому способу идентификации личности, неверие в надежность хранения личных данных ни в государственных учреждениях, ни в частных компаниях;- незаинтересованность банков в передаче биометрических данных своих клиентов в ЕБС, доступную для всех кредитных организаций. Также в статье разработаны конкретные предложения по ускорению распространения биометрии в различных отраслях и сферах деятельности. Сводка и группировка данных Статистическая сводка – это научно организованная обработка материалов статистического наблюдения, ее целью является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально–экономических явлений. Метод группировки. Исходная информация на стадии сводки систематизируется, образуются отдельные статистические совокупности, т.е. осуществляется статистическая группировка. Группировка – это разбиение совокупности на группы, однородные по какому–либо признаку. Особым видом группировки является классификация. Она основывается на самых существенных признаках, которые меняются очень мало (например, классификация видов экономической деятельности, классификация основных фондов). Построение вариационного ряда Для построения вариационного ряда необходимо выполнить следующее. 1. Подсчитать количество вариант (п), входящих в данный вариационный ряд (в нашем примере п = 100); 2. Просмотрев весь материал, найти минимальное и максимальное значения признака (высоты в холке бестужевских коров) для определения размаха изменчивости или лимита (lim = max V - min V). Для нашего примера наибольшая варианта — max v =137 см, минимальная — min v = 119 см; размах изменчивости — lim = 137 - 119 = 18 см; Вычисление основных статистических показателей Основные из них - следующие. 2.1 Средние величины. Среднее арифметическое значение. Этот показатель вычисляется по формуле 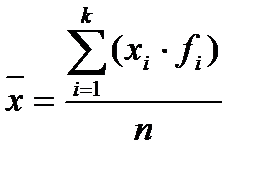 где к — количество классов; xi— значение i-гo класса (середина интервала, если ряд интервальный); —частота i-го класса. Средняя арифметическая величина, вычисленная по формуле , называется - взвешенной. Основные типы распределений признаков Различают дискретные и непрерывные вероятностные распределения. Дискретное распределение характеризуется тем, что оно сосредоточено в конечном или счетном числе точек. Непрерывное распределение "размазано" по некоторому вещественному интервалу Учет ошибок измерения и репрезентативности Систематические ошибки репрезентативности являются результатом преднамеренного и пристрастного отбора единиц из генеральной совокупности, которые должны быть подвергнуты наблюдению. Величина ошибок представительности, или репрезентативности, определяется специальными методами Проведение поисковых опытов Целью поисковых опытов может быть проверка отдельных частей разработанной методики и приспособленности приборов тем измерениям, которые определила методика. Поисковые опыты необходимо ставить для того, чтобы найти основание для расчета количества опытов. Типы вариационных рядов и их графическое изображение. Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности варьирования значений признака. Наиболее широко используются следующие виды графического изображения вариационных рядов: полигон, гистограмма, кумулятивная кривая. Полигон, как правило, служит для изображения дискретного вариационного ряда. Гистограмма служит для изображения только интервального вариационного ряда. Кумулятивная кривая (кривая накопленных частот или накопленных частостей) строится следующим образом. Методология исследования Методология исследования – это важный раздел научной работы, в котором раскрывается теоретический базис исследования. Методология – это не набор методов исследования, а его теоретическая основа, то есть те теории, которые предшествовали рождению нового знания. Способы структурирования полученной информации Структурирование информации – это разделение её по отдельным, схожим критериям на группы, а также выстраивание связей логических цепочек между полученными группами. Иными словами, структурировать информацию означает создать некий визуальный скелет, с помощью которого будет легко запомнить ту или иную информацию. Первичная статистическая обработка данных Статистическая обработка данных основывается на первичных и вторичных количественных методах. Цель первичной обработки статистических данных является структурирование полученных сведений, подразумевающее группировку данных в сводные таблицы по различным параметрам. Сводка и группировка данных Понятие сводки. Статистическая сводка – это научно организованная обработка материалов статистического наблюдения, ее целью является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально–экономических явлений. Метод группировки. Исходная информация на стадии сводки систематизируется, образуются отдельные статистические совокупности, т.е. осуществляется статистическая группировка. Классификация шкал измерения Все виды шкал измерений обычно разделяются на следующие типы: шкалы наименований; шкалы порядка; шкалы интервалов (разностей); шкалы отношений; абсолютные шкалы; условные шкалы. Шкалы интервалов и отношений относят к метрическим шкалам, сюда же относят абсолютные шкалы как подтип шкал отношений Планирование и проведение эксперимента Планирование эксперимента - это процесс выбора условий, процедуры и методов проведения опытов, их числа и условий, необходимых и достаточных для решения поставленной задачи с требуемой точностью. План проведения эксперимента должен включать следующие разделы: 1. Наименование темы исследования. 2. Цель и задачи эксперимента. 3. Условия проведения эксперимента: параметр оптимизации и варьируемые факторы. 4. Методика проведения исследования. 5. Обоснование количества опытов (объема эксперимента). 6. Средства и методика проведения измерений. 7. Материальное обеспечение эксперимента (перечень оборудования). 8. Методика обработки и анализа экспериментальных данных. 9. Календарный план проведения испытаний, в котором указываются сроки их выполнения, исполнители, представляемые данные эксперимента. 10. Смета расходов. Определение условий решения поставленной задачи Анализ экспериментальных данных Единственной целью программы оценки является получение данных для их последующего анализа. Различают два типа данных: 1) численные показатели качества функционирования поисковой системы и 2) данные о неудачах при поиске. После проведения испытания системы одной из первых задач должно быть выявление и суммирование результатов по полноте и точности поиска. Известны два альтернативных способа осреднения численных значений полноты и точности для серии экспериментальных запросов. Как вычисляют непараметрическую среднюю По степени интенсивности развития признака животные могут быть ранжированы в порядке усиления или ослабления выраженности признака. Порядковый номер животного называется рангом Как вычисляют среднюю геометрическую Средняя геометрическая величина ( или Среднее геометрическое ) получается от перемножения данных величин и извлечения из этого произведения корня, показатель которого равен числу этих величин: Как вычисляют среднюю квадратическую Среднеквадратическое отклонение равно квадратному корню из дисперсии: При определении среднего квадратического отклонения при достаточно большом объеме изучаемой совокупности (n > 30) применяются формулы: – среднее квадратическое отклонение простое (или невзвешенное); – среднее квадратическое отклонение взвешенное, где: xi – значения изучаемого признака (варианты); n – объем статистической совокупности; x – средняя арифметическая величина. Как вычисляют среднюю гармоническую Среднее гармоническое значение множества положительных вещественных чисел определяется как результат деления количества этих чисел на сумму их обратных величин: Что такое мода и медиана Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту. Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы. Повышение эффективности процедуры исследования Точность измерений. Действия над приближенными числами То́чность измере́ний, точность результата измерения — близость измеренного значения к истинному значению измеряемой величины. Точность измерений описывает качество измерений в целом, объединяя понятия правильность измерений и прецизионность измерений. Понятие точность также используется как качественная характеристика средства измерений, отражающая близость к нулю его погрешности Действия над приближенными числами Результат действий над приближёнными числами представляет собой также приближённое число. Погрешность результата может быть выражена через погрешности первоначальных данных при помощи следующих теорем: 1. Предельная абсолютная погрешность алгебраической суммы равна сумме предельных абсолютных погрешностей слагаемых. 2. Относительная погрешность суммы заключена между наибольшей и наименьшей из относительных погрешностей слагаемых. 3. Относительная погрешность произведения или частного равна сумме относительных погрешностей сомножителей или, соответственно, делимого и делителя. 4. Относительная погрешность n-ой степени приближенного числа в n раз больше относительной погрешности основания (как у целых, так и для дробных n). Пользуясь этими теоремами, можно определить погрешность результата любой комбинации арифметических действий над приближенными числами. Преобразование выборки к нормальному виду Параметрические критерии оценки различия двух выборок Критерии носят название «параметрические», потому, что в формулу их расчета включаются такие параметры выборки, как среднее, дисперсия и др. Как правило, в психологических исследованиях чаще всего применяются два параметрических критерия – это t - критерий Стьюдента, который оценивает различия средних для двух выборок и F - критерий Фишера, оценивающий различия между двумя дисперсиями. Двухфакторный дисперсионный анализ количественных признаков Двухфакторный дисперсионный анализ (ДДА) служит для изучения влияния на результирующий признак двух различных факторов. ДДА подразумевает формирование и анализ двухфакторных дисперсионных комплексов (ДДК). Регрессионный анализ Регрессио́нный анализ — набор статистических методов исследования влияния одной или нескольких независимых переменных {\displaystyle X_{1},X_{2},...,X_{p}}X_{1},X_{2},...,X_{p} на зависимую переменную {\displaystyle Y}Y. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Корреляция), а не причинно-следственные отношения. Наиболее распространенный вид регрессионного анализа — линейная регрессия, когда находят линейную функцию, которая, согласно определённым математическим критериям, наиболее соответствует данным Группировка первичиых данных Основные характеристики варьирующих объектов Степенные средние (средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя кубическая,средняя геометрическая). Способы вычисления степенных средних. Размах вариации. Дисперсия и ее свойства. Среднее квадратичное отклонение. Коэффициент вариации. Нормированное отклонение. Моменты статистических величин (начальные, условные,центральные). Законы распределеиия Критерии достоверности оценок Дисперсионный анализ Однофакторный дисперсионный анализ количественных признаков Ошибки репрезентативности. Корреляция между признаками. Ложная корреляция Множественная корреляция Показатели разнообразия признаков в совокупности. Доверительный интервал Вычисление средних величин. Установление и способы снижения ошибки измерения Построение вариационного ряда Варьирование. Вариационный ряд Сбор и накопление данных об исследуемых биологических явлениях. Форма учета результатов наблюдений Назовите основные различия между количественными и качественными признаками. Поясните, что такое выборочная и генеральная совокупность. Поясните, какие генетико–статистические параметры характеризуют фенотипический уровень и изменчивость признака? Расскажите, как определяют генетический коэффициент связи между признаками. Какие коэффициенты используют при определении связи между признаками? Опишите основные методы определения коэффициента наследуемости и повторяемости. Какие статистические величины используют при проведении дисперсионного анализа? Расскажите об эффекте селекции. Какие генетические факторы влияют на него? Расскажите, как составляют выборку. Какие выборки называют большими и какие малыми? Расскажите, как составляют вариационный ряд. Какими способами можно графически изобразить вариационные ряды Какие бывают типы распределения и вариационных кривых Перечислите средние величины и их использование Как вычисляется средняя арифметическая величина в малых и больших выборках Какими свойствами обладают средние величины Какие показатели характеризуют разнообразие признака Как вычисляется среднее квадратическое отклонение в малых выборках Как вычисляется среднее квадратическое отклонение в больших выборках Как вычисляется средняя квадратическое отклонение для альтернативных признаков Как вычисляется коэффициент фенотипической корреляции в малых выборках Как вычисляется коэффициент фенотипической корреляции в больших выборках В чем заключается различие связи между признаками при положительных и отрицательных значениях коэффициента корреляции В каких случаях используется коэффициент ранговой корреляции Что характеризуют коэффициенты регрессии В чем различие между коэффициентами r и R Что такое средняя взвешенная В каких случаях она применяется и как её вычисляют В каких случаях вычисляют коэффициент вариации Что такое нормированное отклонение и для чего используется этот показатель Как вычисляют ошибку средней арифметической Как определяют достоверность выборочных показателей Как определяют доверительные границы при работе с большими и малыми выборками Как определяют достоверность разности между выборочными средними арифметическими Что такое критерий соответствия (хи-квадрат) и как он используется В чем заключается цель дисперсионного анализа Что называется общей, факториальной и остаточной дисперсией Какие бывают дисперсионные комплексы. Что они характеризуют. Какие показатели используют для оценки силы и достоверности влияния изучаемого фактора Какие факторы влияют на величину коэффициента наследуемости Есть ли различия в понятиях наследственность, наследование и наследуемость Какой перечень статистических параметров используется для характеристики уровня изменчивости и наследуемости количественных признаков Как составляют однофакторный дисперсионный комплекс и вычисляют вспомогательные величины Какие доверительные вероятности можно использовать в биологических зоотехнических и ветеринарных исследованиях? Как вычисляется коэффициент наследуемости. Каковы его особенности |
