Практическое 4. Пр 4 Порт инвестир. Портфельное инвестирование
 Скачать 56.95 Kb. Скачать 56.95 Kb.
|
|
Портфельное инвестирование Суть портфельного инвестирования состоит в улучшении возможностей инвестирования путем придания совокупности объектов инвестирования тех инвестиционных качеств, которые недостижимы с позиции отдельно взятого объекта, а возможны лишь при их сочетании. Структура инвестиционного портфеля отражает определенное сочетание интересов инвестора. Таким образом, инвестиционный портфель выступает как инструмент, посредством которого достигается требуемая доходность при минимальном риске или соответствующая доходность при требуемом уровне риска. В качестве примера решим задачу, пользуясь исходными данными табл. 1.1 для варианта № 51, где значения доля акций ГазПрома составляют 0,25, доля акций Сбербанка составляют 0,15, доля акций Лукойла составляют 0,15, доля акций НорНикеля составляют 0,25, доля акций РусГидро составляют 0,2. Доходности акций ГазПрома: 12, -5, 6, 0, 3; доходности акций Сбербанка: 11, 5, 0, -5, -10, доходности акций Лукойла: 4, 10, 0, -5, -8, доходности акций НорНикеля: 18, 8, 3, -7, 0, доходности акций РусГидро: -3, -8, 14, 8, 5. Вероятность реализации значения доходности: 0,35; 0,25; 0,2; 0,15; 0,05. Определение средних ожидаемых доходностей акций и общей доходности портфеля. Средняя или ожидаемая доходность Ri i-ого актива равна: Ri = E(r) = p1r1+p2r2+…+pnrn, (1) где rj - возможное j-ое значение доходности актива; pj - вероятность реализации значения доходности j-ого актива; n - число возможных значений доходности. Вероятность реализации значения доходности актива определяется как отношение временного промежутка, в течение которого наблюдается данное значение доходности, ко всему времени наблюдения. Ожидаемая доходность портфеля равна средневзвешенному значению ожидаемых значений доходностей ценных бумаг, входящих в портфель: 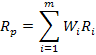 (2) (2)где Rp - ожидаемая норма доходности портфеля Р за период; Wi - вес актива i в портфеле; m - число активов в портфеле. Расчитаем средние ожидаемые доходности акций: ГазПром: Сбербанк: Лукойл: НорНикель: РусГидро: Тогда общая доходность портфеля будет равна: Rp= Определение стандартных отклонений доходностей акций и коэффициентов вариации. Вариация - мера разброса случайной величины вокруг её среднего значения. В математике - математическое ожидание квадрата отклонений случайной величины Х от её среднего значения Е(Х), равная: Формула для определения вариации доходности i-ого актива имеет вид: 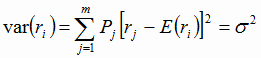 (4) (4)Стандартное отклонение, имеющее ту же размерность, что и доходность, равно: Стандартные отклонения доходности по каждой из акций отражают степень рискованности инвестиции в данную акцию. Для того чтобы сравнить степень риска различных акций с различной средней (ожидаемой) доходностью и различным стандартным отклонением доходности, используется понятие коэффициент вариации: 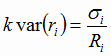 (6) (6)Рассчитаем вариацию активов: ГазПром: var1= Сбербанк: var2= Лукойл: var3= НорНикель: var4= РусГидро: var5= Тогда стандартные отклонения равны: Коэффициенты вариации рассчитаем по формуле представленной выше: Определение коэффициентов ковариации активов. Ковариация и коэффициент корреляции являются мерами взаимозависимости двух случайных величин. Отражают степень согласованности в поведении доходностей активов. Положительная ковариация означает, что в движении доходности двух ценных бумаг имеется тенденция изменяться в одних и тех же направлениях: если доходность одной акции возрастает (или уменьшается), то и доходность другой акции также возрастает (уменьшится). Если же имеет место обратная тенденция, т.е. увеличению (уменьшению) доходности акций одной компании соответствует снижение (увеличение) доходности акций другой компании, то считается, что между доходностями акций этих двух компаний существует отрицательная ковариация. Ковариация двух активов равна : 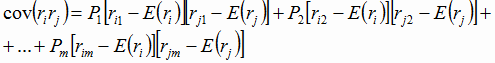 (7) (7)Рассчитаем ковариацию активов: Для наглядности рассчитанные показатели ковариации сведем в таблицу 1. Уточним, что: cov(ri,rj)=cov(rj,ri); cov(ri,ri)=var(ri), следовательно диагональные значения нашей таблицы будут равны значениям вариации активов. cov(r1,r1)= cov(r1,r2)= и т.д. Таблица 1 - Рассчитанные показатели ковариации активов
Определение коэффициентов корреляции активов. С ковариацией связана корреляция, равная ковариации двух активов, деленной на произведение их стандартных отклонений. Коэффициент корреляции между двумя случайными величинами равен: 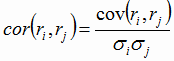 (8) (8)Коэффициент корреляции лежит в пределах от -1 до +1. При этом (+1) означает полное совпадение направления движения, а (-1) - полное несовпадение. Рассчитаем коэффициенты корреляции: cor(r1,r2)= cor(r1,r3)= и т.д. Таблица 2 -Рассчитанные коэффициенты корреляции активов
3.8 Определение стандартного отклонения и коэффициента вариации портфеля. В общем случае для портфеля из M активов вариация доходности равна: 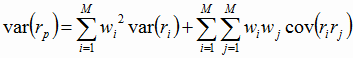 (9) (9)Стандартное отклонение равно: Коэффициент вариации равен: 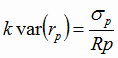 (11) (11)В данном случае формула для расчёта вариации доходности портфеля будет выглядеть следующим образом: var(rp)= W12var(r1)+ W22var(r2)+ W32var(r3)+ W42var(r4)+ W52var(r5)+ +2W1W2cov(r1,r2)+2W1W3cov(r1,r3)+2W1W4cov(r1,r4)+2W1W5cov(r1,r5)+ +2W2W3cov(r2,r3)+2W2W4cov(r2,r4)+2W2W5cov(r2,r5)+2W3W4cov(r3,r4)+ +2 W3W5cov(r3,r5)+2 W4W5cov(r4,r5). (12) Теперь подставим значения: var(rp) = ВЫПОЛНЕНИЕ РАБОТЫ Таблица 3 - Исходные данные
3. Рассчитываются показатели. На основании табл. 3 рассчитывается показатели средних ожидаемых доходностей акций, общей доходности портфеля, стандартных отклонений доходностей акций, коэффициентов вариации, показателей ковариации активов, коэффициентов корреляции активов, стандартного отклонения доходности портфеля и коэффициента вариации доходности. Данные заносятся в табл. 4. Таблица 4 - Таблица расчёта величин планов погашения долга
Задача №2 Рассматривается возможность приобретения облигаций внутреннего валютного займа Минфина России. Имеются следующие данные. Дата выпуска –14.05.1996г. Дата погашения –14.05.2011г. Купонная ставка –3%. Число выплат –1 раз в год. Средняя курсовая цена –93,7. Требуемая норма доходности –14% годовых. Произвести анализ эффективности операции на 25 сентября текущего года. Решение:_Задача_№3'>Решение: Задача №3 Обыкновенные акции предприятия «Ф» продаются по 25,00. В конце периода t=1 ожидаются выплаты дивидендов в размере 2,00. Требуемая инвестором доходность составляет 12%. а) Определите стоимость акции, если ожидается, что в следующие 3 года дивиденды будут расти на 12 % в год, на 4 и 5 год – на 11 %, а начиная с шестого на 5 %. б) Изменит ли текущую стоимость акции предположение о её продаже к концу 5 года? Подкрепите выводы соответствующими расчетами. Решение Задача №4 Рассматривается возможность формирования инвестиционного портфеля из двух акций А и В в равных долях, характеристики которых представлены ниже.
А) исходя из предположения, что коэффициент корреляции между ними равен 0,25., определите ожидаемую доходность и риск портфеля. Б) определите оптимальный портфель для требуемой нормы доходности в 20 % Решение Задача № 5 Текущий курс акции равен 80,00 и может в будущем либо увеличиться до 100,00 с вероятностью 0,6, либо понизиться до 60,00 с вероятностью 0,4. Цена исполнения опциона «колл» равна 80,00. Определите ожидаемую стоимость опциона «колл». Определите коэффициент хеджирования и постройте безрисковый портфель. Решение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
