экзамен кратные интегралы. Последовательность точек nмерного пространства ( Опр координатного и Евклидового пространства, сферические и прямоугольные окрестности, последовательности и его предела, теорема БольцаноВейерштрасса)
 Скачать 497.29 Kb. Скачать 497.29 Kb.
|
|
Последовательность точек n-мерного пространства ( Опр: координатного и Евклидового пространства, сферические и прямоугольные окрестности, последовательности и его предела, теорема Больцано-Вейерштрасса) Рассмотрим упорядоченную совокупность n чисел 𝑥1,𝑥2,…,𝑥𝑛 , где 𝑥𝑖 ∈ 𝐑. Множество всевозможных упорядоченных совокупностей n чисел называется nмерным координатным пространством: 𝐑𝑛. Каждая упорядоченная совокупность 𝑀 (𝑥1,𝑥2,…,𝑥n) - точка 𝐑𝑛. Совокупность точек n-мерного пространства, для которых определено расстояние согласно формуле (1)называется n-мерным Евклидовым пространством и обозначается 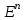 или или 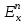 З а м е ч а н и е. В случае Расстояние между точками в 1. 2. 3. Определение 1.3. Пусть каждому натуральному числу Числовую последовательность Определение 1.4.Число А называется пределом данной последовательности При этом пишут Отметим, что неравенство (1.2) эквивалентно Последовательность, у которой существует предел, называется сходящейся. Последовательность, не являющаяся сходящейся, называется расходящейся. 1. Сходящаяся последовательность имеет только один предел. 2. 3. 4. 5. Если 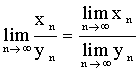 ; ;Теорема ҰБольцано-Вейерштрасса) Из любого ограниченной последовательности точек пространства En можно выделить сходящуюся последовательность. Типы точек и множеств пространства En ( определение точек: предельная, внутренная, граничная. Определение открытого, связного, замкнутого множества, области и выпуклой области)  Пусть точка М (G Определение 3.4 Точка M 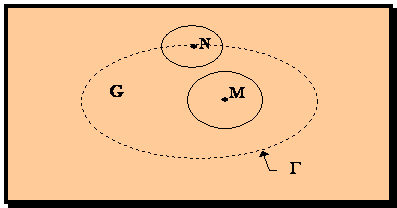 Рис. 3.4 Определение 3.5. Точка N Совокупность всех граничных точек множества G называется его границей ( Г ). Определение3.6. Множество G будем называть областью (или открытым множеством), если все его точки внутренние. Всякое открытое множество, содержащее точку Х, называется ее окрестностью и обозначается О(х). Обозначим Множество S называется связным, если любые две точки этого множества можно соединить непрерывной линией, состоящей из точек данного множества. Пример 3.2. Пусть Г = {x, y: x Определение 3.7. Если у точки х Определение 3.8. Точка х Rn называется предельной точкой некоторого множества А Rn, если 0(х) содержит по крайней мере одну точку множества А, отличную от х. З а м е ч а н и е. Очевидно, что предельная точка является граничной точкой. С другой стороны, всякая граничная точка множества А является либо ее изолированной точкой, либо предельной. Рассмотрим некоторую область D. Если для любой пары точек x1, x2 ∈ D (рис. 1.1) отрезок [x1, x2], включающий конечные точки x1, x2, принадлежит области D, то область называется выпуклой, в противном случае она называется невыпуклой. Предел функции нескольких пременных( Определения: функции, предела по Коши и по Гейне, предел на бесконечности, повторные пределы и их геометрический смысл) Пусть заданы два множества Х и Y. Если каждому элементу х   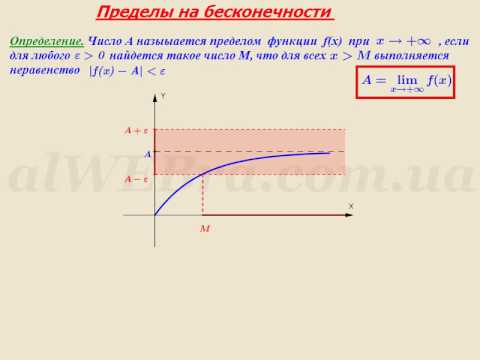  Определение предела функции Определение 3.1. Пусть функция f(х) определена на некотором интервале (а,в), кроме, быть может, точки хо а, в Число А называется пределом функции f(х) в точке хо, т.е. если = х а, в), удовлетворяющих условию х хо х хо f(x) - A (3.2)
х а в х хо х хо f x . Непрерывность функции нескольких переменных на множестве ( определения: непосредственное, по Коши и по Гейне, по приращениям непрерывность в точек по координатам )   Непреравность функции нескольких переменных на множестве ( Определение: непрерывности на множестве, равномерной непрерывности.Теоремы: Вейерштрасса, Больцано-Коши, Кантора) Теорема 1. (Больцано-Коши) Пусть функция f непрерывна на отрезке [a, b], причем f(a) 6= f(b). Тогда для любого числа C, заключенного между f(a) и f(b) найдется точка γ ∈ (a, b), что f(γ) = C. Теорема 2. (первая теорема Вейерштрасса) Если f непрерывна на [a, b], то она ограничена на нем, т.е. существует такое число M, что |f(x)| <=M, при всех x ∈ [a, b]. Теорема 3. (вторая теорема Вейерштрасса) Если f непрерывна на [a, b], то она достигает на нем своей верхней и нижней грани. Определение 1. Функция f называется равномерно-непрерывной на промежутке X, если для любого ε > 0 найдется такая δ = δ(ε) > 0, что для любых двух точек x и x0 из X, удовлетворяющих условию |x − x0| < δ выполняется неравенство |f(x) − f(x0)| < ε Теорема 4. (Кантора) Непрерывная на отрезке [a, b] функция f равномерно непрерывна на этом отрезке. |