Главная страница
Навигация по странице:

  • Практическая работа Тема

  • Задание: Выполните задание по теме: Граф и его элементы.

  • В) Определить кратчайший путь из вершины 1 в вершину 8 для графа, представленного на рисунке; С) Запишите номера вершин, имеющих одинаковую степень

  • Задание: Выполните задание по теме: Граф и его элементы. Граф задан диаграммой. А) Составьте маршруты длины 5 из вершины V

  • Задание: Выполните задание по теме: Понятие дерева в теории графов

  • Задание: Графы и логические задачи

  • Задание: Выполните задание по теме: Сетевые графы

  • Пояснения к работе: Необходимые формулы: Граф

  • Простой граф

  • Пустым

  • Маршрут

    		•

    Вот. пр.раб. Д. Построение графа по условиям ситуационных задач


    Скачать 138.79 Kb.
    НазваниеПостроение графа по условиям ситуационных задач
    Дата05.12.2022
    Размер138.79 Kb.
    Формат файлаdocx
    Имя файлапр.раб. Д.docx
    ТипПрактическая работа
    #828413

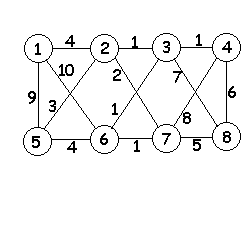
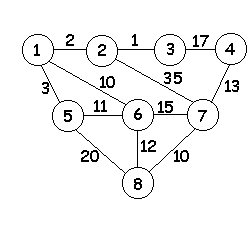
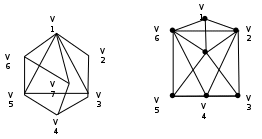
    Выполнить практическую работу. 1 Вариант- 1 столбец, 2вариант- 2 столбец

    Прислать выполненные задания до 13.25 ч ( ПОЗЖЕ НЕ ПРИНИМАЮ)

    На каждой странице своей работы маркером (текстовыделителем) писать свою фамилию.

    Задания присылать на почту aleksandra-sidorova1@yandex.ru
    Практическая работа

    Тема: Построение графа по условиям ситуационных задач.

    Цель работы: Закрепить и систематизировать знания по теме: «Основы дискретной математики».

    Задание: Выполните задание по теме: Граф и его элементы.

    А) Запишите количество ребер и вершин графа;

    В) Определить кратчайший путь из вершины 1 в вершину 8 для графа, представленного на рисунке;

    С) Запишите номера вершин, имеющих одинаковую степень:

    1.


    4.


    2.


    5.


    3.



    6.


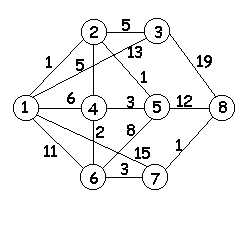
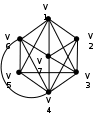
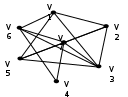
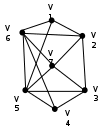
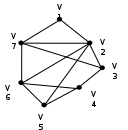
    Задание: Выполните задание по теме: Граф и его элементы.

    Граф задан диаграммой.

    А) Составьте маршруты длины 5 из вершиныV2 в вершину V5. Составьте простую цепь, соединяющую эти вершины.

    В) Постройте простой цикл, содержащий вершину V4.

    С) Определите вид заданного графа

    7.



    10.



    8.







    11.




    9.


    12.



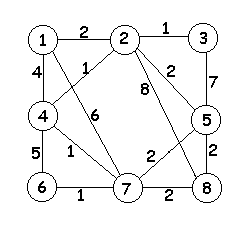
    Задание: Выполните задание по теме: Понятие дерева в теории графов:

    13.
    Сколько различных способов обедов можно выбрать в вагоне-ресторане, если бы на каждый обед выбирать одно холодное блюдо, одно первое, одно второе, одно третье? В меню на этот раз были выставлены студень, красная икра, свежепосоленная рыба; на первое – уха из стерляди, щи с грибами; на второе – осетрина жаренная, теленок жареный на вертеле; на третье – арбузы, груши.
    16.
    Перечислите все возможные сочетания деловой одежды, если у вас в гардеробе брючный костюм черного цвета, белая и голубая блузки, синяя юбка и серый джемпер.

    14.
    Изобразите дерево возможных исходов при троекратном бросании монеты.
    17.
    Волейбольная сетка имеет вид прямоугольника размером 5×10 клеток. Какое наибольшее число верёвочек можно перерезать так, чтобы сетка не распалась на куски?

    15.
    Нарисуйте граф с семью вершинами, в котором для любых двух вершин существует только один связывающий их путь.
    18.
    Рассади участников «Большой восьмерки» за круглым столом всеми возможными способами.

    Задание: Графы и логические задачи:

    19.
    В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что:

    • Вода и молоко не в бутылке.

    • Сосуд с лимонадом стоит между кувшином и сосудом с квасом.

    • В банке не лимонад и не вода.

    • Стакан стоит между банкой и сосудом с молоком.

    В каком сосуде находится, какая из жидкостей?
    22.
    Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7-и 11-литровых сосудов и крана с водой отмерить 2 литра?

    20.
    На улице, встав в кружок, беседуют Аня, Валя, Галя и Надя.

    • Девочка в зеленом платье – не Аня и не Валя – стоит между девочкой в голубом платье и Надей.

    • Девочка в белом платье стоит между девочкой в розовом и Валей. Какого цвета платье у каждой из девочек?
    23.
    В семье четверо детей. Им 5, 8, 13 и 15 лет. Зовут их Аня, Боря, Вера и Галя. Сколько лет каждому ребенку, если одна девочка ходит в детский сад, Аня старше Бори, а сумма лет Ани и Веры делится на три?

    21.
    В Артеке за круглым столом оказалось пятеро ребят из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алеша, Коля и Витя. Москвич сидел между Томичем и Витей, санкт-петербуржец – между Юрой и Толей, а напротив него сидел пермяк и Алеша. Коля никогда не был в Санкт-Петербурге, Юра не бывал в Москве и Томске, а Томич с Толей регулярно переписываются. Определите, кто в каком городе живет.
    24.
    Беседуют трое друзей – Белокуров, Рыжов и Чернов. Брюнет сказал Белокурову: «Любопытно, что один из нас – блондин, другой – брюнет, третий – рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос у каждого из друзей?



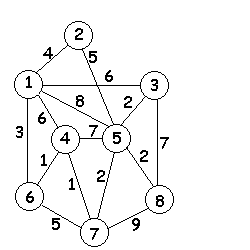
    Задание: Выполните задание по теме: Сетевые графы: В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Числа, стоящие на пересечениях строк и столбцов означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Укажите схему, соответствующую таблице.

    25.




    A
    B
    C
    D
    E
    F

    A



    5












    B
    5



    9
    3
    8



    C



    9






    4



    D



    3






    2



    E



    8
    4
    2



    7

    F












    7






    28.




    A
    B
    C
    D
    E
    F

    A



    2












    B
    2



    3
    2
    3



    C



    3






    2



    D



    2






    1



    E



    3
    2
    1



    6

    F












    6






    26.




    А
    В
    С
    D

    А



    4



    5

    В
    4



    3
    6

    С



    3






    D
    5
    6









    29.




    A
    B
    C
    D
    E
    F

    A



    4












    B
    4



    6
    3
    6



    C



    6






    4



    D



    3






    2



    E



    6
    4
    2



    5

    F












    5





    27.




    А
    В
    С
    D
    Е

    А



    1
    4



    1

    В
    1






    3



    С
    4









    2

    D



    3









    E
    1



    2









    30.




    А
    В
    С
    D
    Е

    А






    3
    1



    В






    4



    1

    С
    3
    4






    2

    D
    1












    E



    1












    Пояснения к работе:

    Необходимые формулы:

    Граф- это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными.

    Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.

    Если ребра не имеют ориентации, граф называется неориентированным.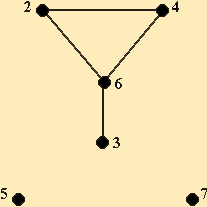


    Петля- это дуга, начальная и конечная вершина которой совпадают.

    Простой граф- граф без кратных ребер и петель.

    Степень вершины- это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.

    Пустым называется граф без ребер.

    Полным называется граф, в котором каждые две вершины смежные.

    Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.

    Маршрут в графе путь, ориентацией дуг которого можно пренебречь.

    Цепь- маршрут, в котором все ребра попарно различны.

    Цикл- замкнутый маршрут, являющийся цепью.

    Граф называется связным, если любая пара его вершин связана.

    Дерево — это связный граф без циклов.

    Содержание отчета

    1. Титульный лист

    2. Цель работы

    3. Задание

    4. Выполненная практическая работа в соответствии с заданием

    5. Ответы на контрольные вопросы

    6. Вывод

    Контрольные вопросы:

    1. Дайте определение графа.

    2. Сформулируйте понятие смежных ребер. Запишите формулу суммы степеней графа

    3. Дайте определение правильного графа, изолированной вершины графа.

    написать администратору сайта