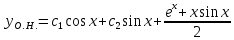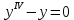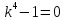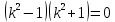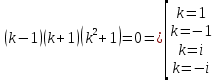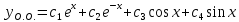ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Петербургский государственный университет путей сообщения
Императора Александра I»
(ФГБОУ ВО ПГУПС)
Кафедра «Высшая математика»
Специальность 23.05.05 «Системы обеспечения движения поездов»
Специализация «Электроснабжение железных дорог»
Курсовая работа
по дисциплине
«Математика»
на тему: «Построение и исследование математической модели линейного динамического звена»
Форма обучения – очная
Выполнил обучающийся
Курс 2
Группа ЭС-805
|
__________________
подпись, дата
|
Калинин Е.Н.
|
|
|
|
Руководитель
|
__________________
подпись, дата
|
Благовещенская Е.А.
|
Санкт-Петербург
2019
Оглавление
1.Теоретическая часть 1
Пункт1 .Виды дифференциальных уравнений 1 порядка: 1
Пункт 2. Дифференциальное уравнение с разделяющимися переменными 1
Пункт 4 . Линейные уравнения 1 порядка 3
Пункт 5. Дифференциальное уравнение Бернулли 4
Пункт 7. Виды линейных дифференциальных уравнений высших порядков с постоянными коэффициентами. 5
Пункт 8 .Уравнения, допускающие понижение порядка 8
Пункт 9 . Решение ЛНДУ со специальной правой частью 9
2. Практическая часть 10
2.9.Неоднородное Дифференциальное уравнение второго порядка 19
2.10. Неоднородное Дифференциальное уравнение второго порядка со смещаемой правой частью 20
2.11. Неоднородное Дифференциальное уравнение второго порядка со специальной правой частью.(Метод неопределенных коэффициентов) 20
Теоретическая часть Пункт1 .Виды дифференциальных уравнений 1 порядка:
- стандартный вид уравнений 1 порядка. стандартный вид уравнений 1 порядка.
Пункт 2. Дифференциальное уравнение с разделяющимися переменными
Вид уравнения.
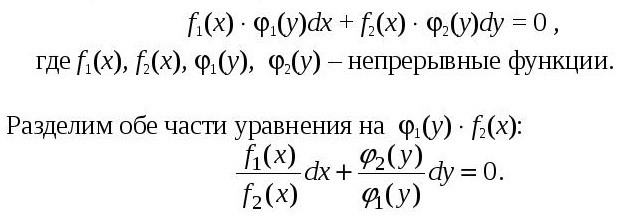
Полученное уравнение с разделенными переменными проинтегрировать.
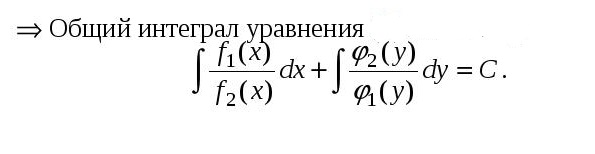
Пункт 3. Однородное дифференциальное уравнение 1 порядка. 

Пункт 4 . Линейные уравнения 1 порядка
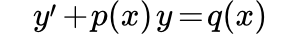
Метод Лагранжа (вариации постоянной):

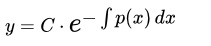

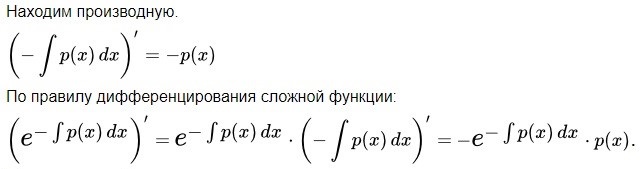
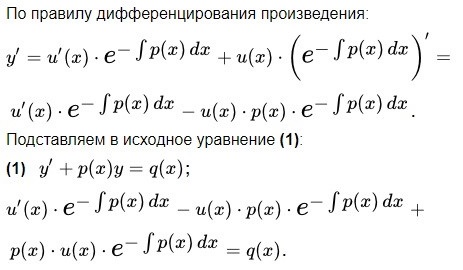

Пункт 5. Дифференциальное уравнение Бернулли
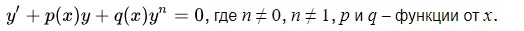 (1) (1)

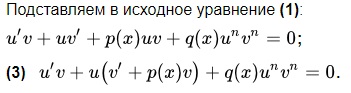


Пункт 6. Дифференциальное уравнение первого порядка в полных дифференциалах – это уравнение вида:

Если найдена такая функция U(x, y), то уравнение принимает вид:
dU(x, y) = 0.
Его общий интеграл:
U(x, y) = C,
где C – постоянная.

Пункт 7. Виды линейных дифференциальных уравнений высших порядков с постоянными коэффициентами.
Линейные однородные дифференциальные уравнения.
Вид уравнения:
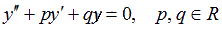
Первым шагом необходимо найти корни характеристического уравнения
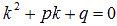
1) 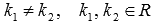 - корни характеристического уравнения действительные и различающие. - корни характеристического уравнения действительные и различающие.
Тогда общее решение ДУ:
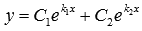
2) 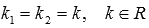 - корни действительными и совпадающие. - корни действительными и совпадающие.
Общее решение ДУ:
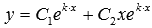
3) 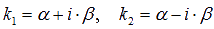 - корни комплексно сопряженные. - корни комплексно сопряженные.
Общее решение ДУ:
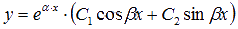
Линейные неоднородные дифференциальные уравнения.

Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного и частного решения неоднородного уравнения:
yон = yоо + yчн .
Методы нахождения частного решения неоднородных ДУ второго порядка:
Существует несколько методов нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами. Эти методы выбираются в зависимости от вида правой части – функции 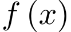 . .
1) Если функция 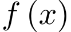 представляет собой многочлен n-ой степени представляет собой многочлен n-ой степени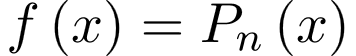 , то частное решение уравнения ищется в виде , то частное решение уравнения ищется в виде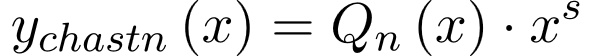
Здесь 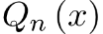 – многочлен степени n с неопределенными коэффициентами (которые подлежат определению), а s – кратность корня – многочлен степени n с неопределенными коэффициентами (которые подлежат определению), а s – кратность корня 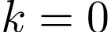 характеристического уравнения однородного уравнения или то есть количество корней характеристического уравнения, равных нулю). характеристического уравнения однородного уравнения или то есть количество корней характеристического уравнения, равных нулю).
 Так как Так как 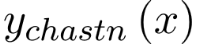 – частное решение уравнения, то коэффициенты, определяющие многочлен – частное решение уравнения, то коэффициенты, определяющие многочлен 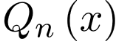 , можно найти методом неопределенных коэффициентов из равенства , можно найти методом неопределенных коэффициентов из равенства
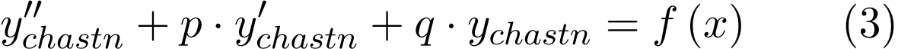
использовав тот факт, что два многочлена равны, если равны коэффициенты при соответствующих степенях независимой переменной.
2) Если функция 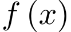 , стоящая в правой части уравнения, имеет вид , стоящая в правой части уравнения, имеет вид
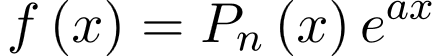 то есть представляет собой произведение многочлена степени n и экспоненты, то частное решение этого уравнения ищется в виде то есть представляет собой произведение многочлена степени n и экспоненты, то частное решение этого уравнения ищется в виде
 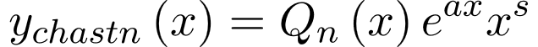
где 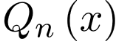 – многочлен степени n с неопределенными коэффициентами, а s – кратность корня – многочлен степени n с неопределенными коэффициентами, а s – кратность корня 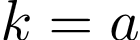 в характеристическом уравнении соответствующего однородного уравнения (или то есть количество корней характеристического уравнения, равных a). в характеристическом уравнении соответствующего однородного уравнения (или то есть количество корней характеристического уравнения, равных a).
Коэффициенты многочлена 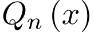 определяются подстановкой частного решения определяются подстановкой частного решения 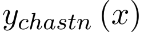 в исходное уравнение (так как в исходное уравнение (так как 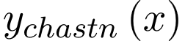 является решением, то оно должно удовлетворять уравнению). является решением, то оно должно удовлетворять уравнению).
Таким образом, должно выполняться равенство.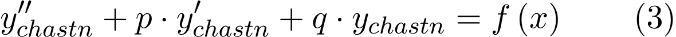
3) Если правая часть неоднородного дифференциального уравнения имеет вид:
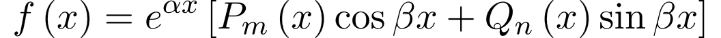
то частное решение в этом случае ищем в виде:
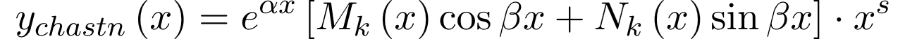
 Здесь s – число комплексно сопряженных пар корней характеристического уравнения Здесь s – число комплексно сопряженных пар корней характеристического уравнения 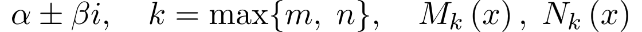 – многочлены степени k с неизвестными коэффициентами. Коэффициенты этих многочленов определяются из равенства – многочлены степени k с неизвестными коэффициентами. Коэффициенты этих многочленов определяются из равенства 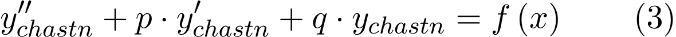
Если правая часть 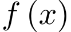 имеет отличную, от описанных выше, структуру, то для нахождение решения уравнения применяют метод вариации произвольной постоянной: имеет отличную, от описанных выше, структуру, то для нахождение решения уравнения применяют метод вариации произвольной постоянной:
1) находится общее решение соответствующего линейного однородного уравнения в виде
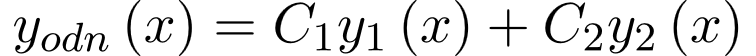
где 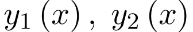 – линейно независимые частные решения линейного однородного дифференциального уравнения, – линейно независимые частные решения линейного однородного дифференциального уравнения, 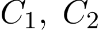 – некоторые произвольные постоянные; – некоторые произвольные постоянные;
2) варьируются произвольные постоянные, то есть считается, что они являются функциями независимой переменной x: 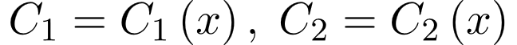
А в качестве общего решения исходного дифференциального уравнения рассматривается функция 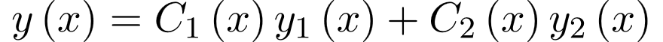
 Функции Функции 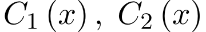 (точнее их производные (точнее их производные  ) являются решением системы ) являются решением системы
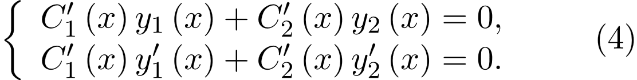
Тогда сами неизвестные функции 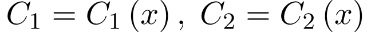 находятся с помощью интегрирования и получим общее решение исходного уравнения. находятся с помощью интегрирования и получим общее решение исходного уравнения.
Пункт 8 .Уравнения, допускающие понижение порядка
Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной данное ДУ сводится к уравнению, порядок которого ниже.
Рассмотрим 3 типа уравнений, допускающих понижение порядка.
Пусть дано уравнение y’’=f(x). Порядок можно понизить, введя новую функцию p(x), положив y’=p(x). Тогда y’’=p’(x) и получаем ДУ первого порядка: p’=f(x). Решив его, т.е. найдя функцию р=р(х), решим уравнение у’=р(х). Получим общее решение заданного уравнения y’’=f(x).
Пусть дано уравнение y’’=f(x;y’), не содержащее явно искомой функции у.
Обозначим у’=р, где р=р(х) – новая неизвестная функция. Тогда у’’=p’ и уравнение y’’=f(x;y’) принимает вид р’=f(x;p). Пусть р= 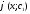 - общее решениеполученного ДУ первого порядка. Заменяя функцию р на у’, получаем ДУ: y’= - общее решениеполученного ДУ первого порядка. Заменяя функцию р на у’, получаем ДУ: y’= 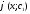 . Оно имеет вид y’’=f(x). Для отыскания у достаточно проинтегрировать последнее уравнение. Общее решение уравнения y’’=f(x;y’) будет иметь вид . Оно имеет вид y’’=f(x). Для отыскания у достаточно проинтегрировать последнее уравнение. Общее решение уравнения y’’=f(x;y’) будет иметь вид
у= 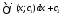 . .
Частным случаем уравнения y’’=f(x;y’) является уравнение y’’=f(y’), не содержащее также и независимую переменную х. Оно интегрируется тем же способом: y’=p(x), y’’=p’= . Получаем уравнение p’=f(p) с разделяющимися переменными.
Рассмотрим уравнение y’’=f(y;y’), которое не содержит явно
независимой переменной х.
Для понижения порядка уравнения введем новую функцию р=р(у), зависящую от переменной у, полагая y’=p. Дифференцируем это равенство по х, учитывая, что р=р(у(х)):
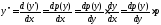 , т.е. = , т.е. =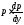 . Теперь уравнениеy’’=f(y;y’) запишется в виде . Теперь уравнениеy’’=f(y;y’) запишется в виде 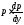 =f(y;p). =f(y;p).
Пусть р=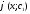 является общим решением этого ДУ первого порядка. Заменяя функцию р(у) на y’, получаем y’= является общим решением этого ДУ первого порядка. Заменяя функцию р(у) на y’, получаем y’=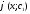 - ДУ с разделяющимися переменными. Интегрируя его, находим общий интеграл уравнения y’’=f(y;y’): - ДУ с разделяющимися переменными. Интегрируя его, находим общий интеграл уравнения y’’=f(y;y’):
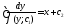 . .
Частным случаем уравнения y’’=f(y;y’) является ДУ y’’=f(y). Такое уравнение решается при помощи аналогичной подстановки: y’=p(y), y’’=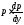 . .
Пункт 9 . Решение ЛНДУ со специальной правой частью
1. Пусть правая часть уравнения (1) имеет вид 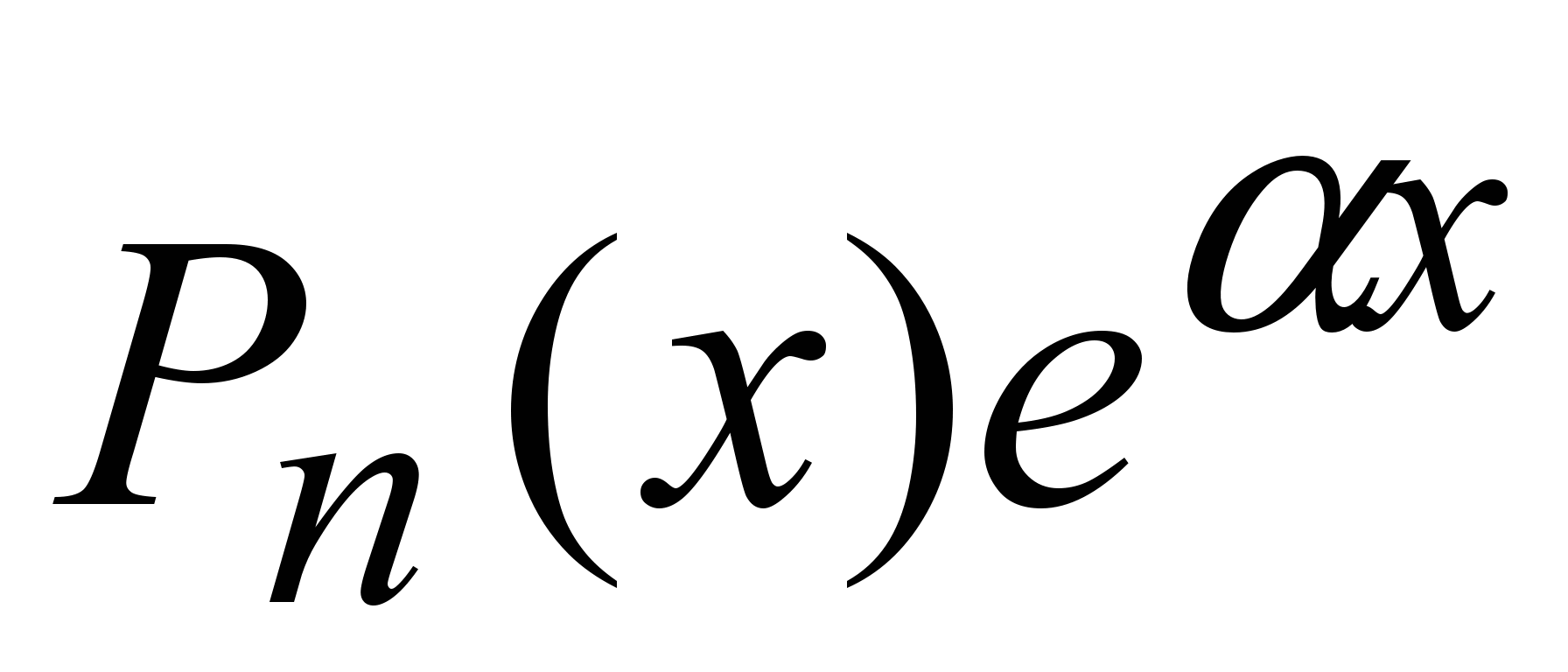 , где , где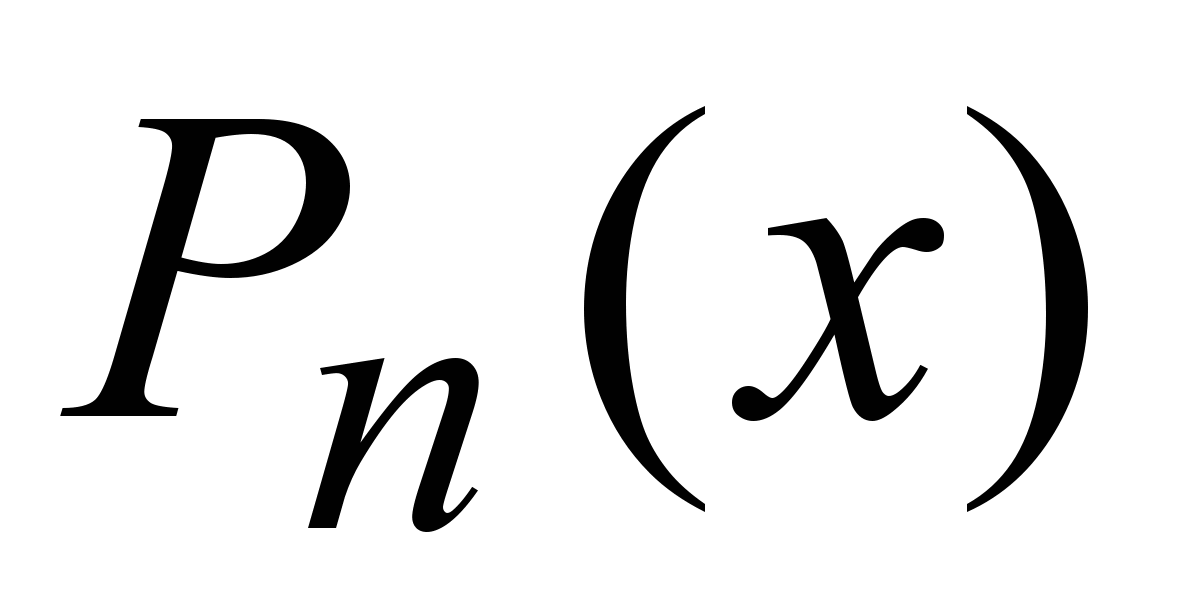 – многочлен n-ной степени: – многочлен n-ной степени:
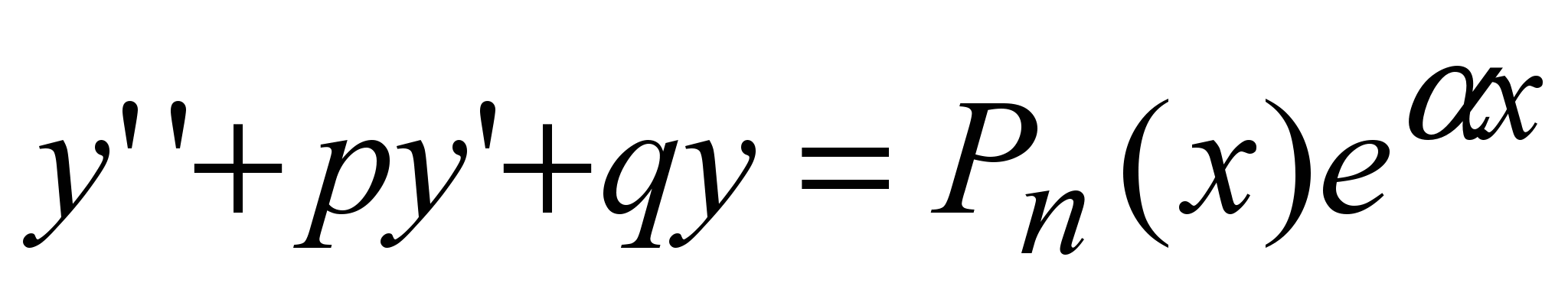 (6) (6)
Тогда возможны следующие случаи:
а) Число не является корнем характеристического уравнения
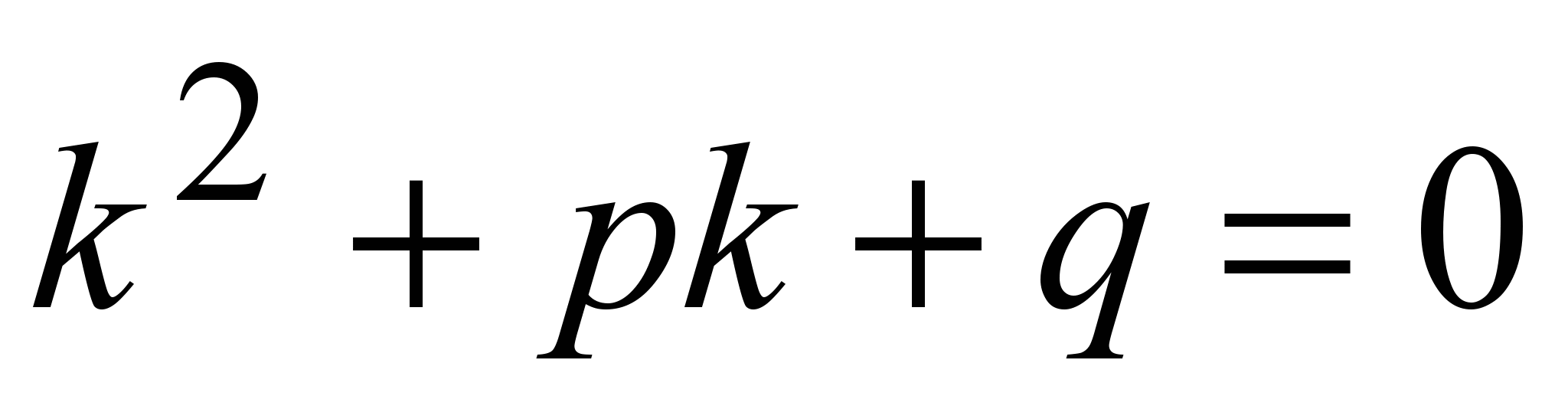 (7) (7)
Тогда частное решение уравнения (6) будем искать в виде
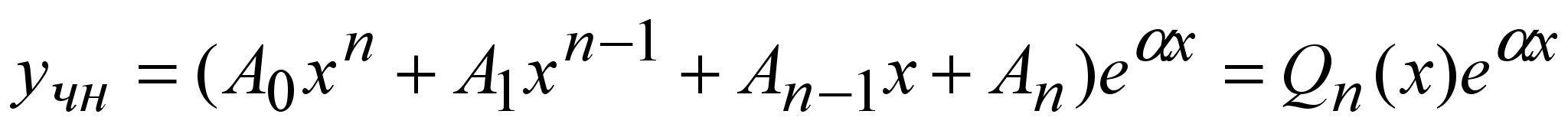 (8) (8)
Подставим его в (6) с учетом вида производных
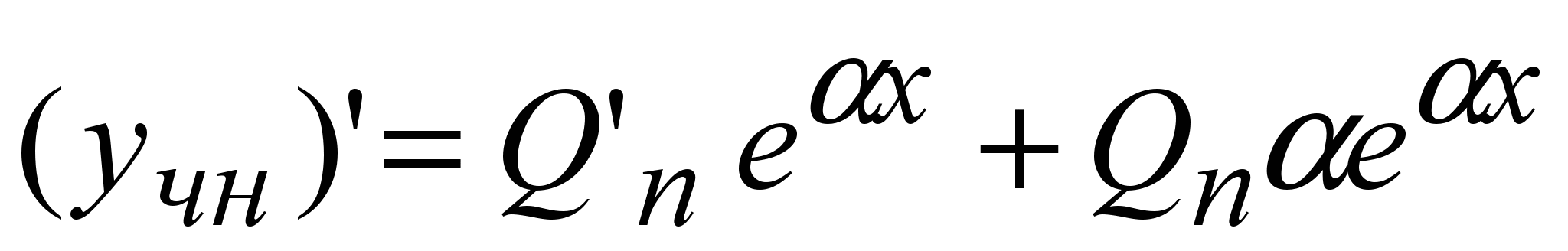
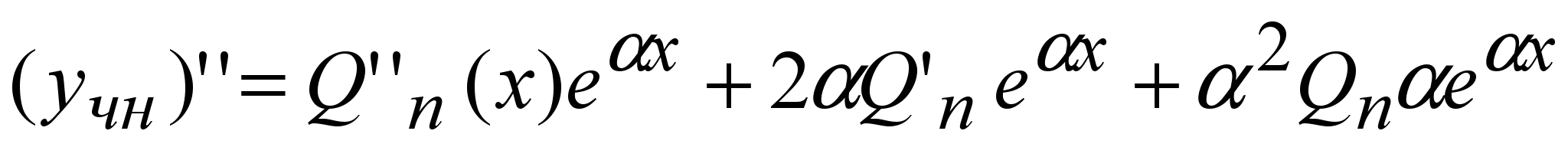
и сокращая на 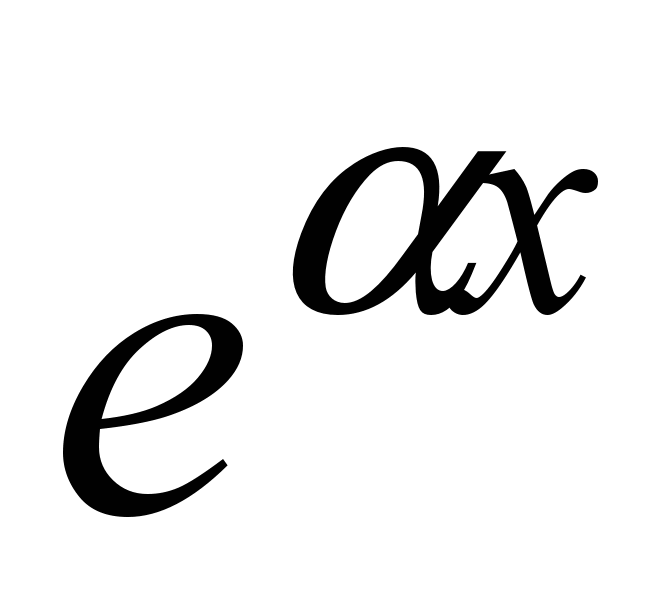 , получим: , получим:
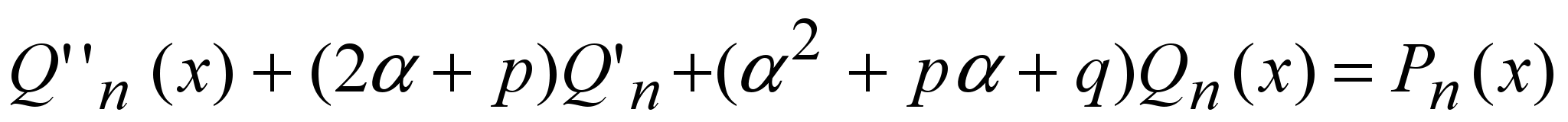 (9) (9)
Если  не является корнем характеристического уравнения, то не является корнем характеристического уравнения, то 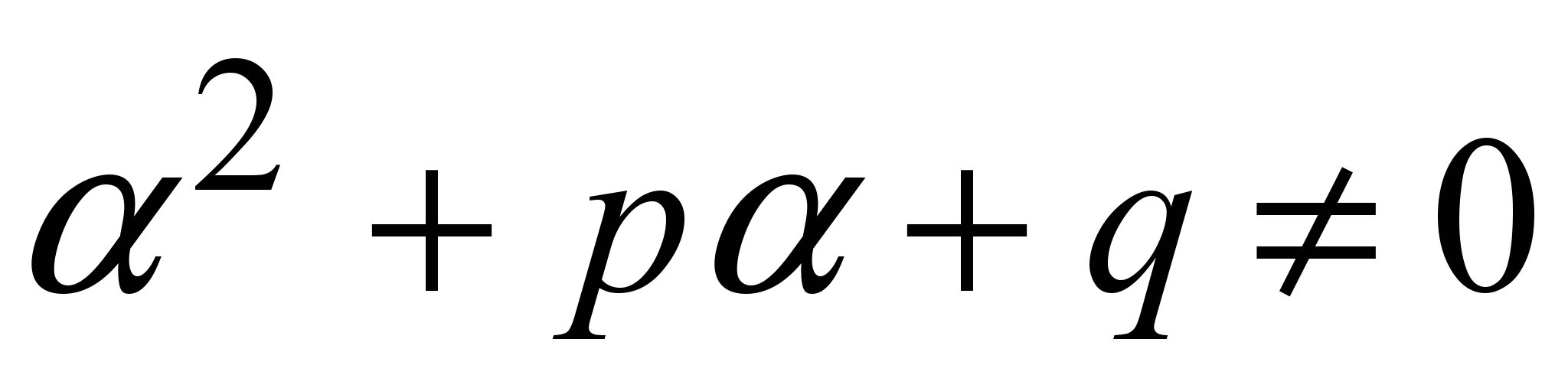 и слева в уравнении (9) – полином n-ного порядка, приравнивая коэффициенты при равных степенях х слева и справа в (9), получим n+1 уравнение с n+1 неизвестной и слева в уравнении (9) – полином n-ного порядка, приравнивая коэффициенты при равных степенях х слева и справа в (9), получим n+1 уравнение с n+1 неизвестной 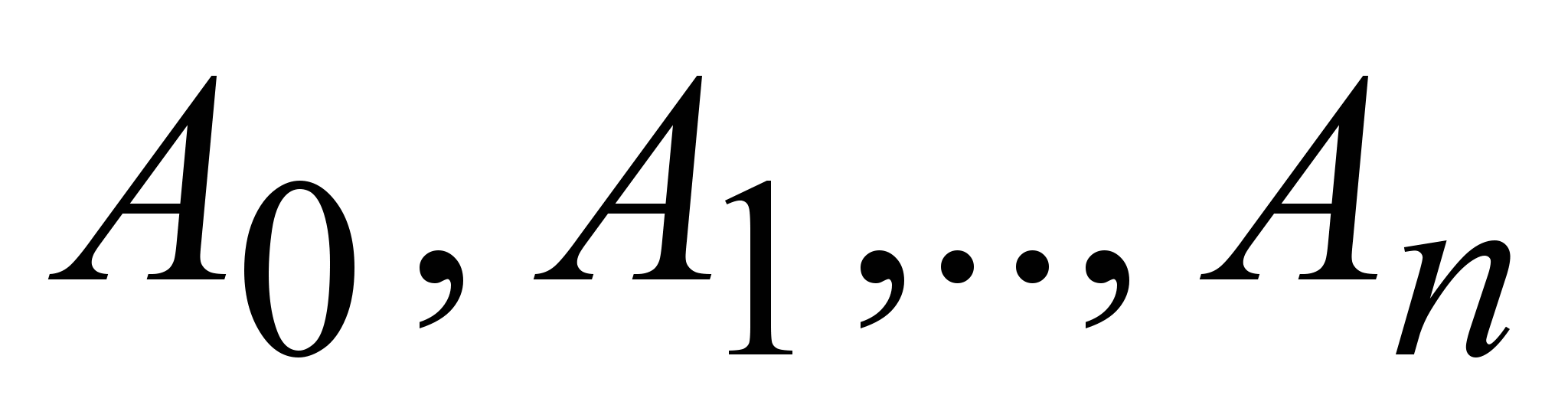 , найдем их и получим частное решение (8). , найдем их и получим частное решение (8).
б) Число  есть однократный корень характеристического уравнения (7) (резонанс). есть однократный корень характеристического уравнения (7) (резонанс).
Тогда в уравнении (9) не будет 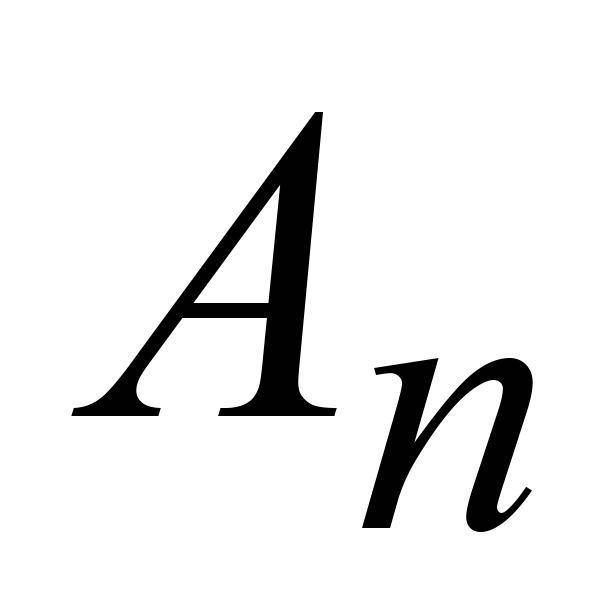 , и слева — полином (n+1)-й степени, а справа – n-й степени, и мы не сможем его найти. , и слева — полином (n+1)-й степени, а справа – n-й степени, и мы не сможем его найти.
В этом случае частное решение ищется в виде
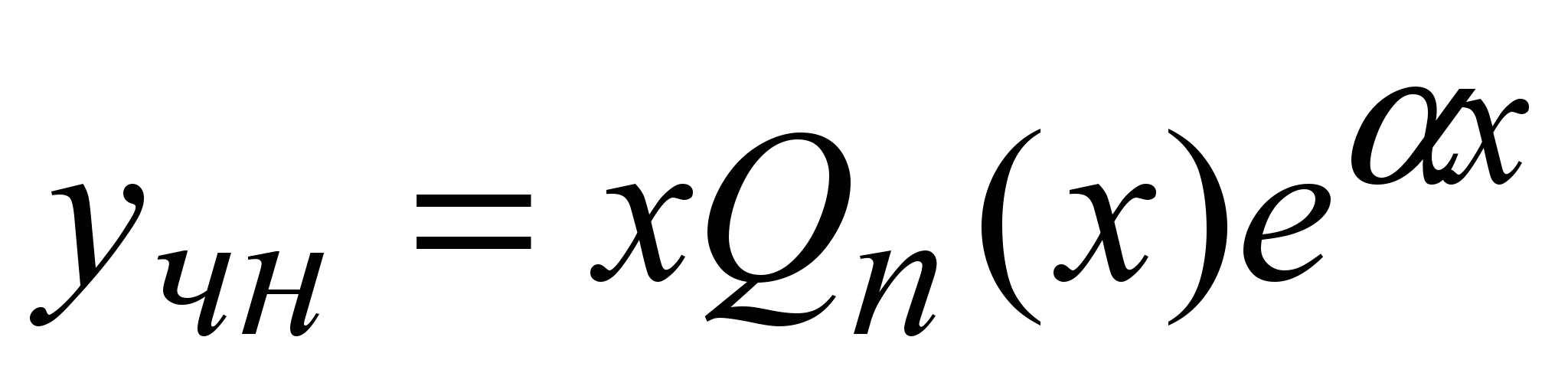 (10) (10)
в) Число  есть двукратный корень характеристического уравнения, есть двукратный корень характеристического уравнения, 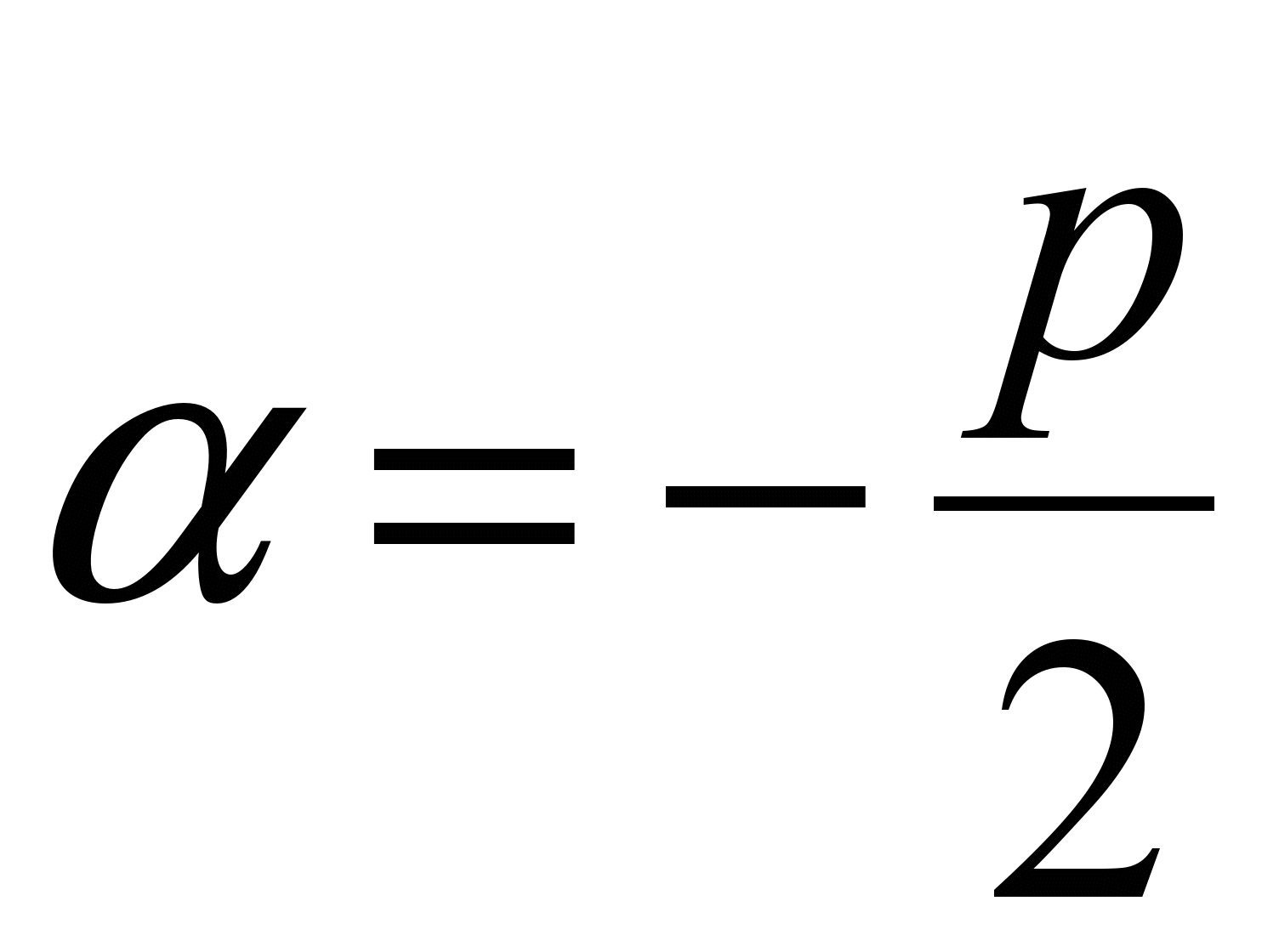 . .
Тогда в уравнении (9) 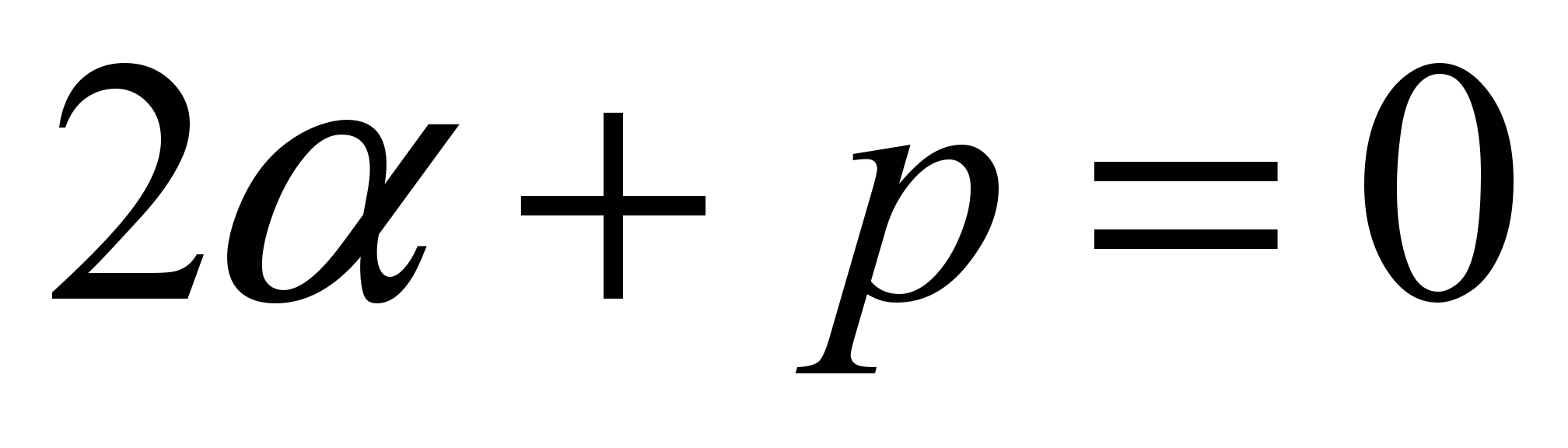 и слева- полином (n-2) степени, а справа- n-й степени. Частное решение будем искать в виде и слева- полином (n-2) степени, а справа- n-й степени. Частное решение будем искать в виде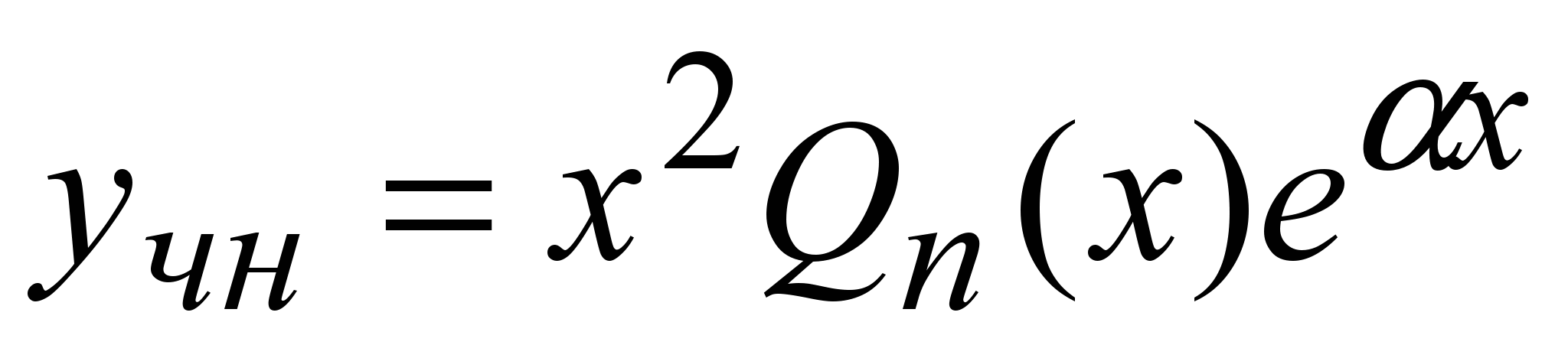 (11) (11)
Практическая часть
Дифференциальное уравнение с разделяющимися переменными
(Пункт 2)
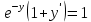 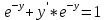 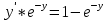 | : | :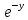
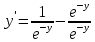 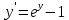 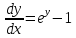 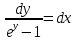 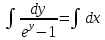 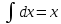 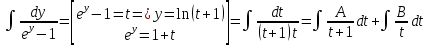  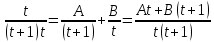 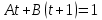 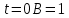 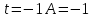  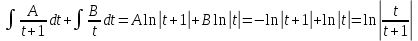 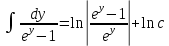 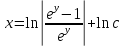 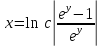 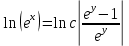 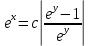 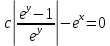 Ответ : Ответ :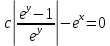
Однородное дифференциальное уравнение первого порядка
(Пункт 3)
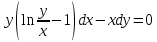  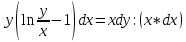 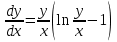 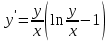 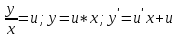 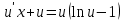 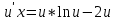 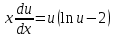 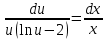 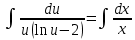 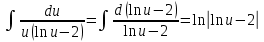 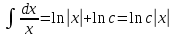 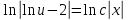 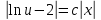 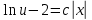 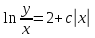 Ответ : Ответ :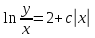
Линейное неоднородное дифференциальное уравнение
(пункт 7)
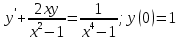 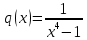 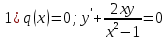 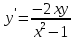 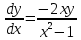 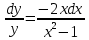 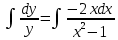 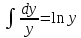 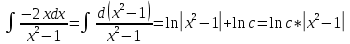 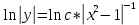 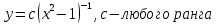 2) 2)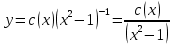 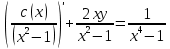 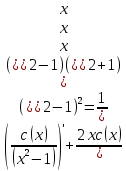 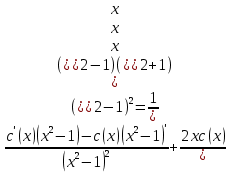 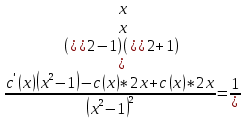 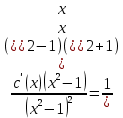 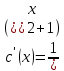 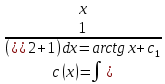 3) 3)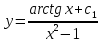 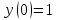 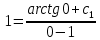 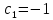 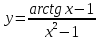 Ответ : Ответ :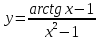
Дифференциальное уравнение Бернулли
(пункт 5)
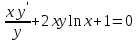 Это уравнение Бернулли Это уравнение Бернулли
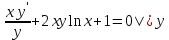 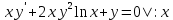 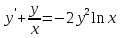 1) 1)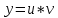 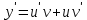 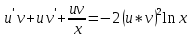 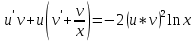 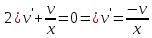 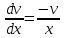 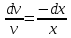 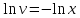 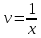 3) 3) 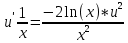 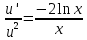 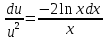 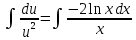 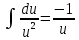 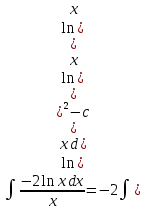 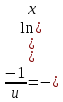 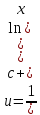 4) 4)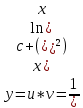
Ответ :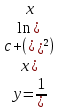
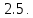 Дифференциальное уравнение в полных дифференциалах Дифференциальное уравнение в полных дифференциалах 6) 6) 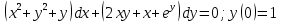 Это уравнение в полных дифференциалах Это уравнение в полных дифференциалах
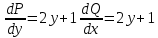 Уравнение в полных дифференциалах dU=0 Уравнение в полных дифференциалах dU=0
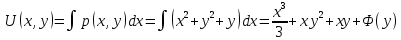 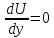 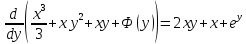 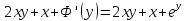 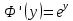 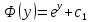 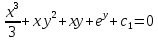 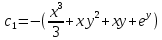 y(0)=1 y(0)=1
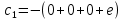 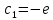 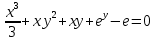 Ответ : U(x,y)= Ответ : U(x,y)=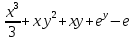
Дифференциальное уравнение, допускающее понижения порядка
(Пункт 8) 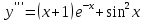 Это уравнение, допускающее понижения порядка Это уравнение, допускающее понижения порядка
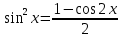 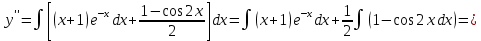 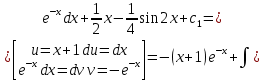 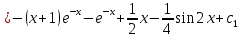 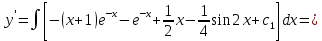 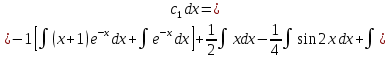 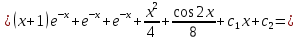 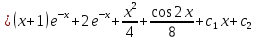 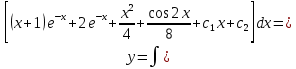 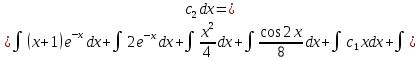 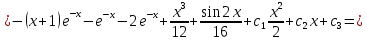 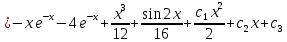 Ответ: y Ответ: y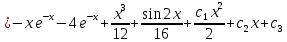
Дифференциальное уравнение, допускающее понижения порядка
(Пункт 8) 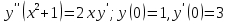
Это уравнение, допускающее понижения порядка
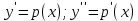 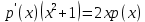 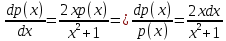 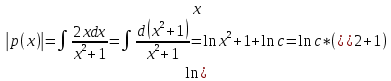 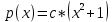 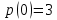 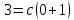 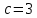 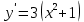 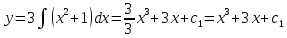 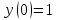 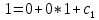 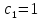 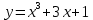 Ответ: Ответ: 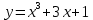
Дифференциальное уравнение, допускающее понижения порядка
(Пункт 8) 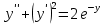 Это уравнение, допускающее понижение порядка Это уравнение, допускающее понижение порядка
 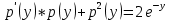 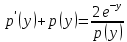 1) 1) 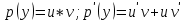
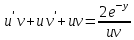 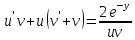 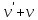 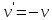 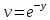 2) 2)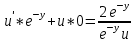
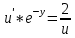 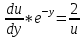 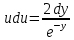 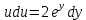 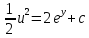 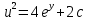 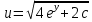 3) 3)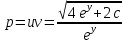
4)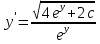
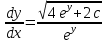 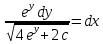 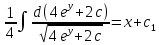 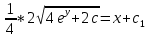 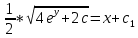  Ответ: Ответ: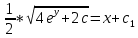
Неоднородное Дифференциальное уравнение второго порядка
(Пункт 7.) 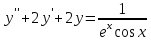 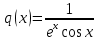 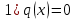 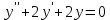 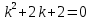 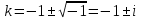 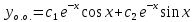 2) 2)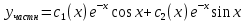
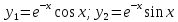 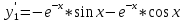 ; ; 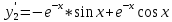
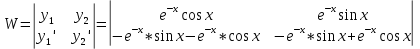 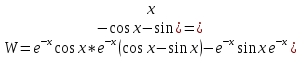 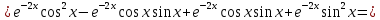 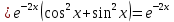 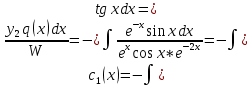 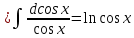 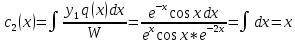 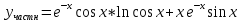 4) 4)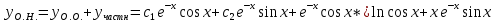
Ответ :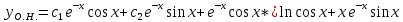
2.10. Неоднородное Дифференциальное уравнение второго порядка со смещаемой правой частью
(Пункт 7.)
 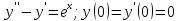
А)Метод неопределённых коэффициентов
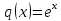 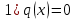 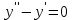 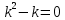 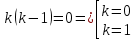 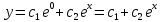 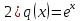 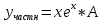 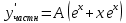 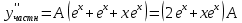 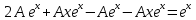 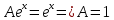 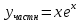 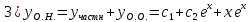 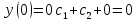 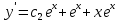 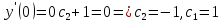 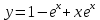 Ответ : Ответ : 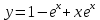
Б) Операционный метод
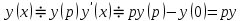 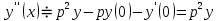 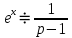 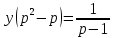 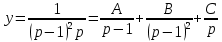 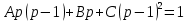 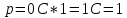 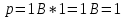 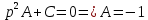 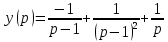 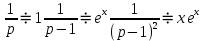  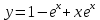 Ответ : Ответ : 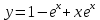
2.11. Неоднородное Дифференциальное уравнение второго порядка со специальной правой частью.(Метод неопределенных коэффициентов)
(Пункт 9.)
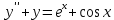
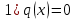 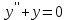 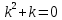 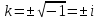 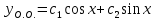 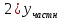 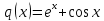 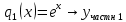 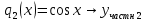 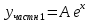 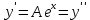 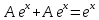 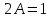 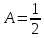 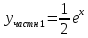 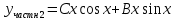 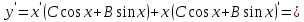 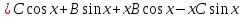 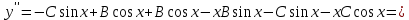 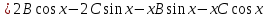 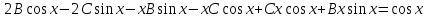 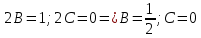 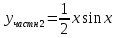 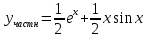 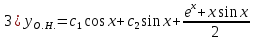 Ответ: Ответ: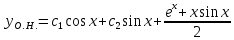
2.12. Однородное дифференциальное уравнение 4 порядка
(пункт 7.) 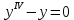 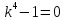 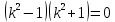 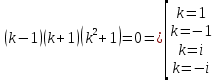 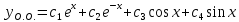  Ответ: Ответ: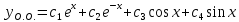 |
 Скачать 1.13 Mb.
Скачать 1.13 Mb.
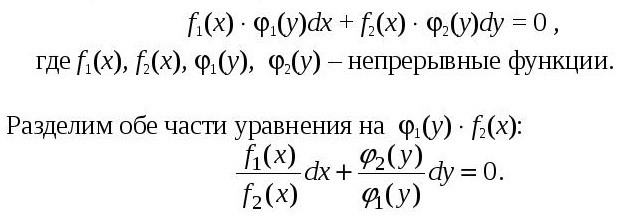
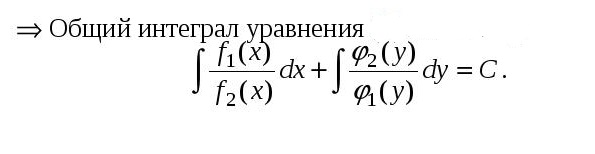




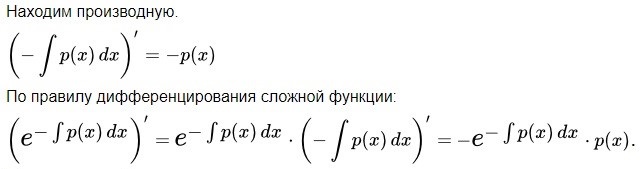
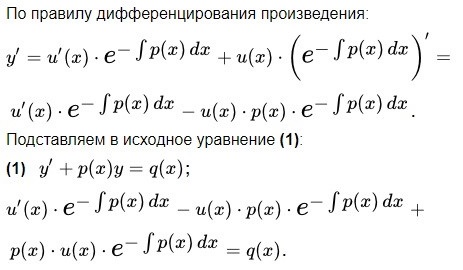


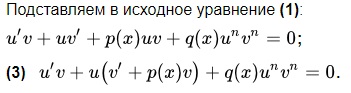





 Так как
Так как 
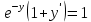
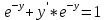
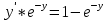 | :
| :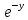
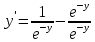
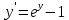
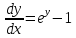
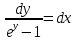
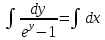
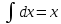
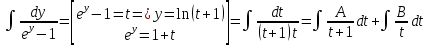

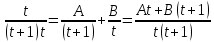
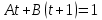
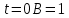
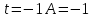
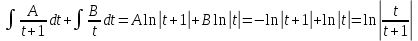
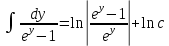
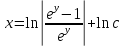
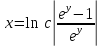
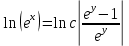
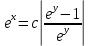
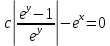
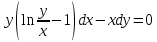
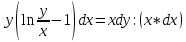
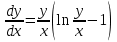
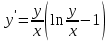
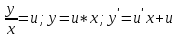
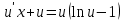
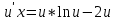
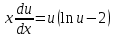
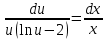
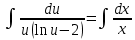
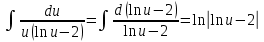
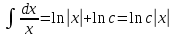
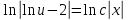
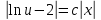
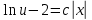
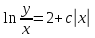 Ответ :
Ответ :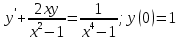
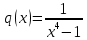
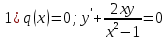
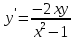
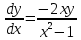
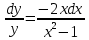
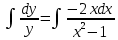
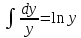
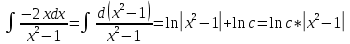
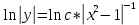
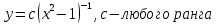 2)
2)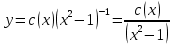
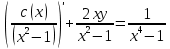
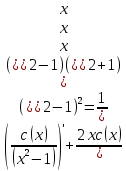
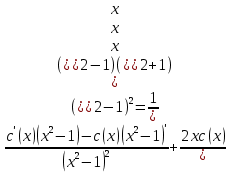
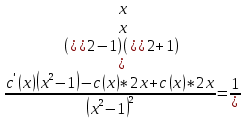
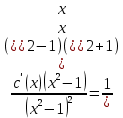
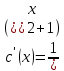
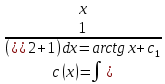 3)
3)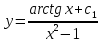
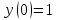
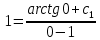
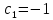
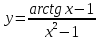 Ответ :
Ответ :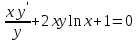 Это уравнение Бернулли
Это уравнение Бернулли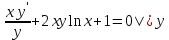
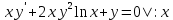
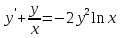 1)
1)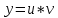
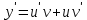
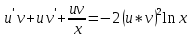
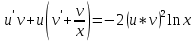
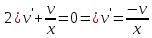
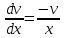
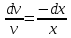
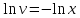
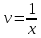 3)
3) 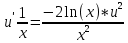
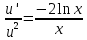
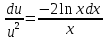
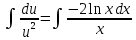
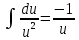
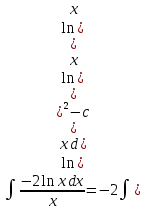
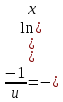
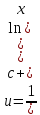 4)
4)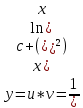
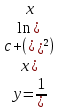
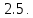 Дифференциальное уравнение в полных дифференциалах
Дифференциальное уравнение в полных дифференциалах
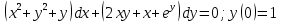
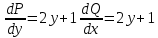 Уравнение в полных дифференциалах dU=0
Уравнение в полных дифференциалах dU=0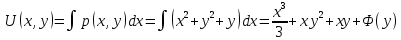
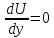
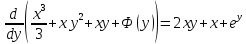
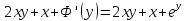
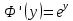
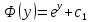
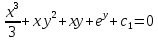
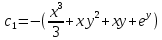 y(0)=1
y(0)=1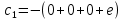
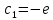
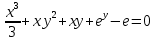 Ответ : U(x,y)=
Ответ : U(x,y)=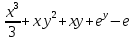
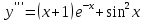 Это уравнение, допускающее понижения порядка
Это уравнение, допускающее понижения порядка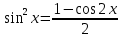
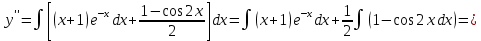
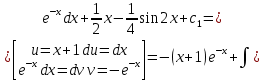
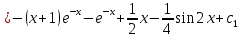
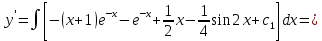
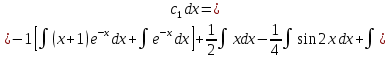
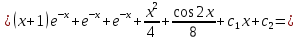
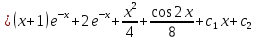
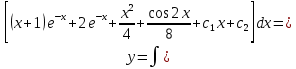
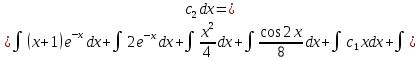
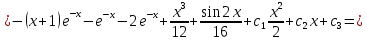
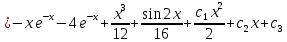 Ответ: y
Ответ: y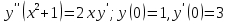
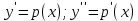
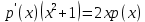
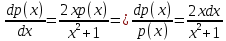
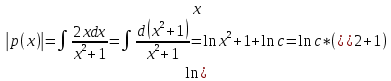
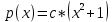
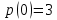
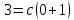
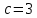
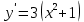
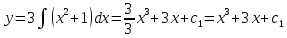
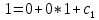
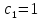
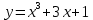 Ответ:
Ответ: 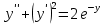 Это уравнение, допускающее понижение порядка
Это уравнение, допускающее понижение порядка
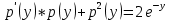
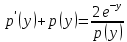 1)
1) 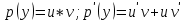
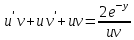
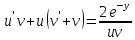
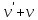
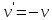
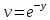 2)
2)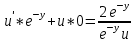
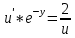
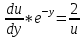
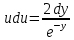
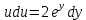
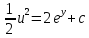
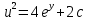
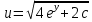 3)
3)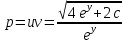
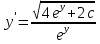
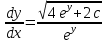
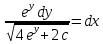
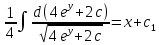
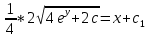
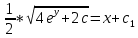
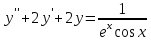
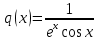
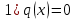
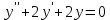
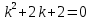
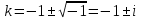
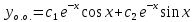 2)
2)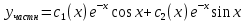
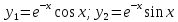
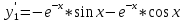 ;
; 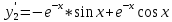
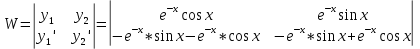
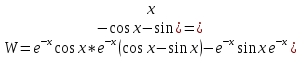
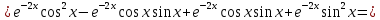
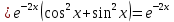
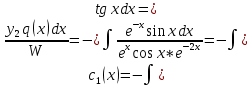
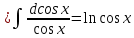
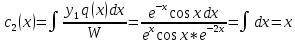
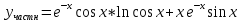 4)
4)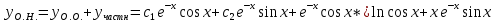
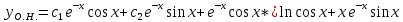
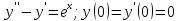
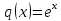
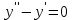
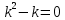
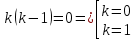
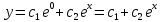
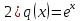
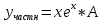
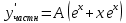
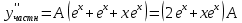
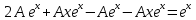
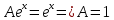
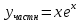
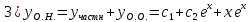
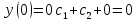
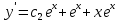
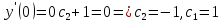
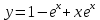 Ответ :
Ответ : 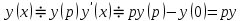
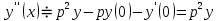
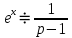
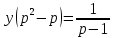
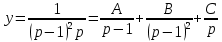
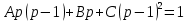
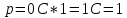
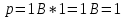
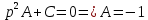
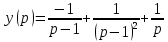
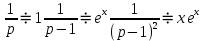
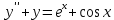
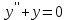
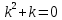
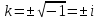
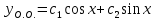
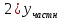
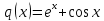
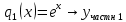
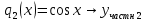
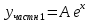
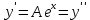
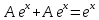
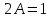
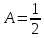
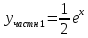
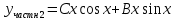
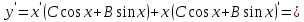
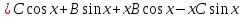
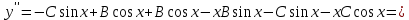
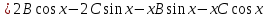
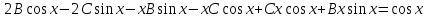
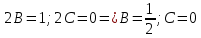
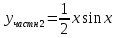
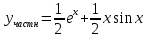
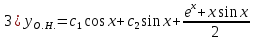 Ответ:
Ответ: