работа. Лабораторная работа 1 (1). Построение моделей идентификации

• Название: Построение моделей идентификации
• Анкор: работа
• Дата: 19.04.2023
• Размер: 0.82 Mb.
• Имя файла: Лабораторная работа 1 (1).doc
• Тип: Лабораторная работа; #1073878
• страница: 1 из 4

Лабораторная работа 1

Тема: «Построение моделей идентификации»
1.1. Задание:

1. 
   Методами регрессионного анализа построить модель идентификации второго порядка .
   
2. 
   Провести статистический анализ модели.
   
3. 
   Проверить целесообразность включения в модель члена третьего порядка, т.е. перехода к модели .
   

Для получения выборки «экспериментальных» данных необходимо осуществить математический эксперимент с уравнением

, (1.1)

в котором величина x измеряется точно, а с ошибкой , имеющей нормальное распределение с нулевым математическим ожиданием и единичной дисперсией Коэффициенты уравнения (1.1) и значение d выбираются в соответствии с вариантом задания из табл.1.1.

Математический эксперимент проводится по следующей схеме:

• 
  с помощью датчика равномерно распределенных на отрезке [0, 1] случайных чисел определяется случайное число
  
• 
  величина x определяется нормированием случайного числа на интервал [0, d]
  
• 
  c помощью датчика нормально распределенных [0, 1] случайных чисел определяется случайное число , представляющее собой «ошибку» эксперимента
  
• 
  «экспериментальная» величина определяется по (1.1) как сумма регулярной и случайной составляющих.
  

Результатом математического эксперимента является выборка 10 случайных пар .

Таблица 1.1

Исходные данные для проведения

математического эксперимента

Вариант				d
1	1	3	-0,2	12
2	0,1	4	-0,3	12
3	4	8	-0,8	8
4	0,6	11	-0,8	10
5	2	5	-0,6	11
6	0,5	2	-0,2	9
7	0,1	9	0,9	7
8	0,8	12	-1	10
9	5	19	-2	8
10	0,4	2	0,1	12
11	3	6	-0,7	8
12	0,5	9	-0,7	9
13	0,1	5	-0,4	9
14	4	18	-2	7
15	0,7	9	-0,7	9
16	8	20	-2	8
17	0,2	10	-1	8
18	0,9	9	0,9	8
19	15	16	-1,5	8
20	0,4	12	-1	9

1.2. Теоретические сведения

1.2.1. Выбор формы идентификации и регрессионный анализ

Математически задача идентификации формулируется следующим образом. Имеется n пар экспериментальных точек . Требуется построить зависимость (модель)

, (1.2)

которая описывает характеристики изучаемой системы. Уравнение (1.2) называется уравнением регрессии.

Построение модели идентификации начинается с выбора формы модели, т.е. вида зависимости (1.2). При этом на практике могут встретится два случая.

• 
  Форма математической модели известна заранее. В этом случае задача идентификации сводится к определению коэффициентов этой модели.
  
• 
  Форма математической модели заранее неизвестна. В этом случае целесообразно использовать для построения модели общее разложение функции в ряд Тейлора.
  

В данной лабораторной работе при идентификации ставится задача нахождение приближенной модели в виде полинома степени p

.

Согласно методу наименьших квадратов, искомый вектор нах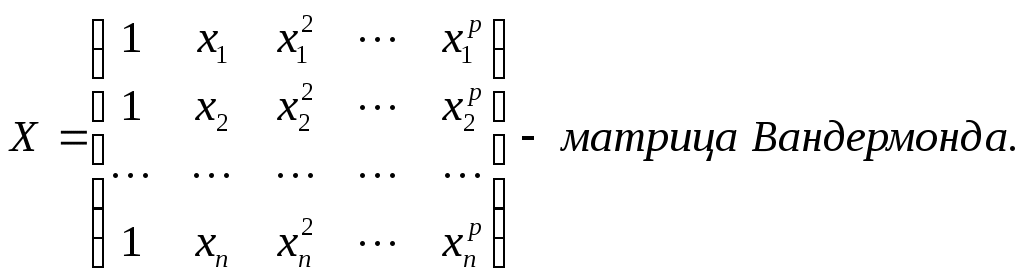одится из решения нормального уравнения

,

где



Таким образом, для определения коэффициентов уравнения регрессии необходимо произвести следующие операции:

• 
  составить матрицу независимых переменных Вандермонда и матрицу-столбец результатов , здесь m число коэффициентов регрессии(m=p+1).
  
• 
  найти транспонированную матрицу переменных и произвести перемножение матриц ;
  
• 
  найти обратную матрицу и умножить ее на матрицу , т.е. получить искомую матрицу-столбец .
  

1.2.2. Статистический анализ модели

После вычисления коэффициентов регрессии необходимо провести статистический анализ полученной модели. Для этого необходимо вычислить следующие характеристики регрессионной зависимости:

• 
  величину остаточной суммы квадратов отклонений фактических значений от ее теоретических значений и число степеней свободы модели
  

;

• 
  средние квадраты остаточных сумм
  

• 
  критерий Фишера
  

здесь - дисперсия, характеризующая ошибку эксперимента.

F – отношение характеризуется двумя последовательно записанными значениями степеней свободы числителя и знаменателя. При этом, так как точность статистических оценок возрастает с ростом числа степеней свободы, то число степеней свободы точной величины принимается равным .

Полученную величину F – отношения сравнивают с критическим (пороговым) значение критерия Фишера при соответствующих числах степеней свободы и заданном уровне значимости . При - модель принимается. Если расхождение результатов моделирования и экспериментальных данных значимо и, следовательно, модель должна быть отвергнута как недостаточно точная.

• 
  оценку связи коэффициентов регрессии между собой .
  

Эта оценка проводится по ковариационной матрице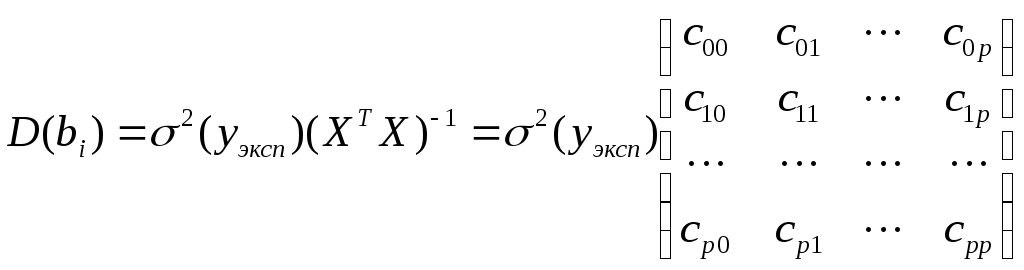

.

Диагональные элементы матрицы определяют дисперсии коэффициентов регрессии, а недиагональные – взаимосвязь этих коэффициентов.

Коэффициент корреляции может изменяться в пределах .
Для сравнения моделей необходимо:

• 
  рассчитать дополнительную сумму квадратов
  

,

где - остаточная сумма квадратов первой и второй модели соответственно;

• 
  определить число степеней свободы дополнительной суммы квадратов
  

;

• 
  посчитать средний квадрат дополнительной суммы
  

;

• 
  определить роль дополнительной информации с помощью критерия Фишера
  

.

Если полученное значение критерия Фишера значимо , то дополнительная информация, заложенная в модель 2 существенна, и модель 2 действительно отличается от модели 1. В противном случае уточнения, вносимые моделью 2, неразличимы на фоне шума; с точки зрения модели равноценны и предпочтение должно быть отдано более простой модели 1.
1.3. Пример построения модели идентификации
Для получения выборки «экспериментальных» данных осуществим математический эксперимент с уравнением

(1.3)

по следующей схеме:

• 
  с помощью датчика равномерно распределенных на отрезке [0, 1] случайных чисел определяется случайное число
  
• 
  величина x определяется нормированием случайного числа на интервал [0, 6]
  
• 
  c помощью датчика нормально распределенных [0, 1] случайных чисел определяется случайное число , представляющее собой «ошибку» эксперимента
  
• 
  «наблюдаемая» величина определяется по (1.3) как сумма регулярной и случайной составляющих.
  

Результаты математического эксперимента (выборка 10 случайных пар ), представлены в виде точек на рис.1.1 (ряд 3).

Построим модель идентификации . Согласно методу наименьших квадратов, искомый вектор коэффициентов находится из решения нормального уравнения

. (1.4)

Найдем составляющие уравнения (1.4)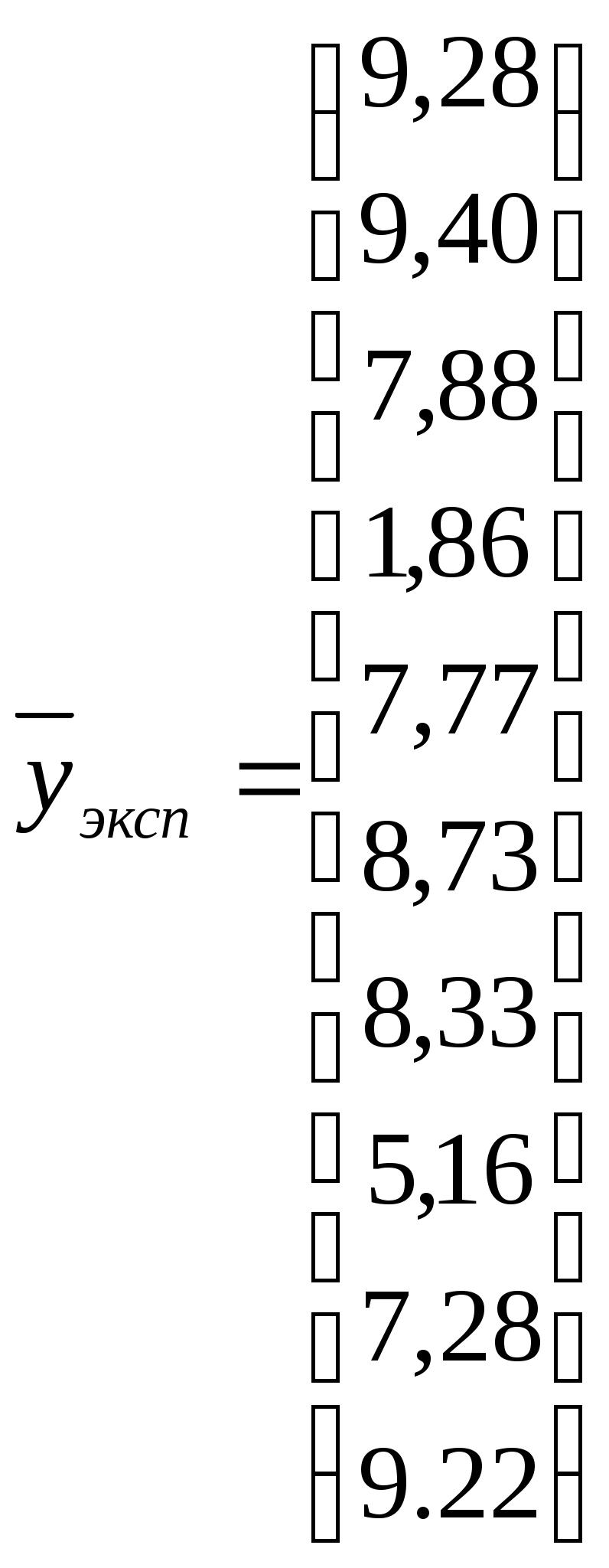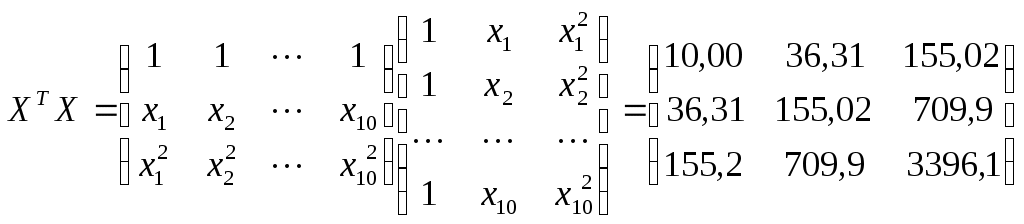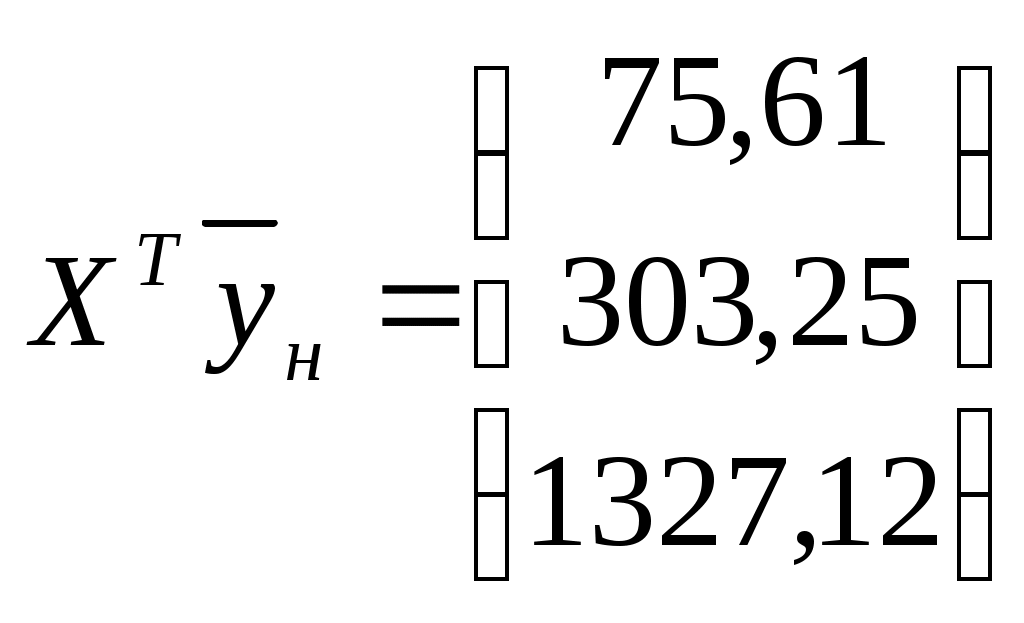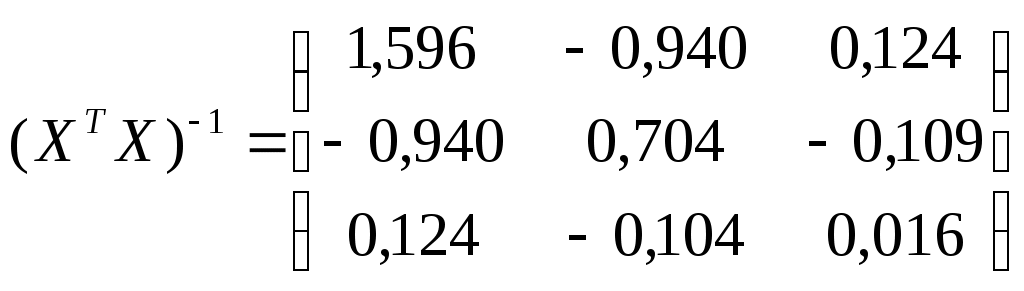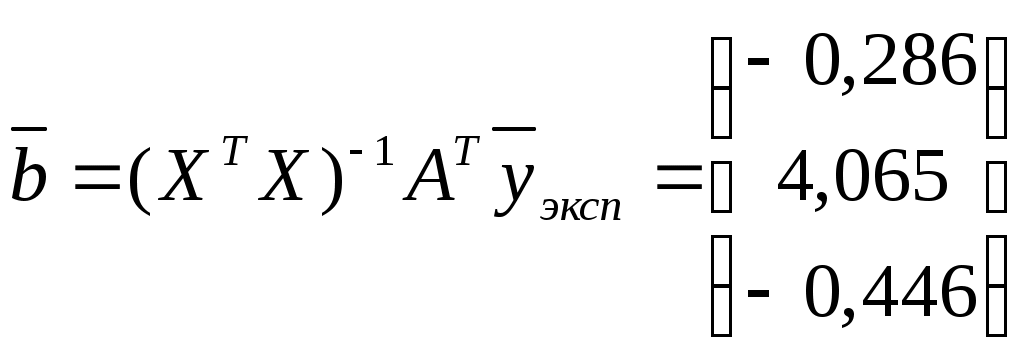












Таким образом, получена зависимость



на рис.1.1- ряд 2. Из рисунка видно, что полученная модель качественно правильно воспроизводит исходное описание.

Статистические характеристики модели имеют следующие значения:

• 
  остаточная сумма квадратов
  

;

• 
  число степеней свободы остаточной суммы квадратов
  

• 
  средние квадраты остаточных сумм
  

;

• 
  критерий Фишера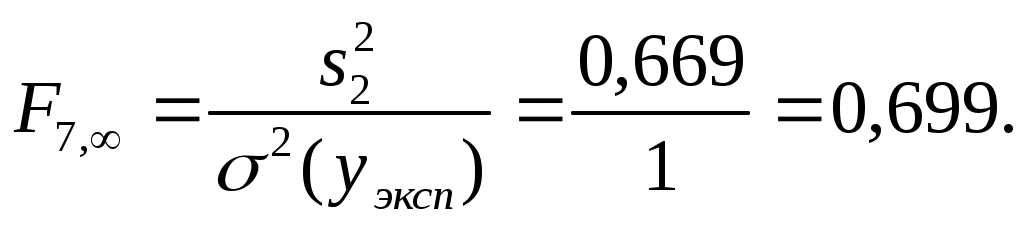
  

По таблицам распределения критерия Фишера , при 5%-м уровне значимости находим критическое значение . Так как полученное значение F меньше критического, гипотеза об адекватности модели реальному процессу принимается.

Определим связи коэффициентов регрессии между собой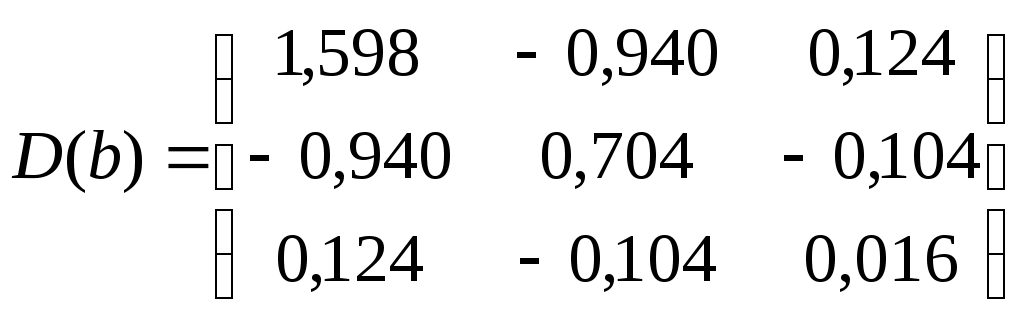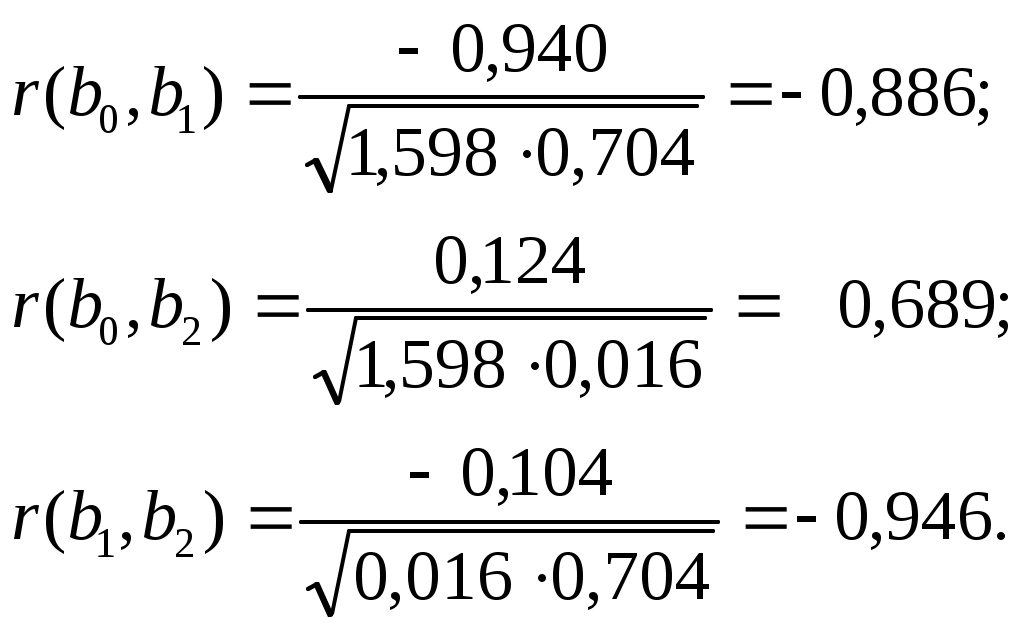

;



Таким образом, коэффициенты регрессии достаточно сильно связаны между собой.
Поскольку форма модели заранее неизвестна, целесообразно рассмотреть возможность использования кубической модели

.

В результате расчетов найдены коэффициенты такой модели

(1.5)

на рис.1.1 – ряд 1.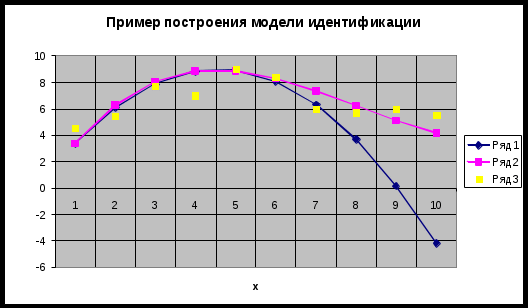


Для проверки целесообразности включения в модель члена третьей степени вычисляется остаточная сумма квадратов для уравнения (1.5), дополнительная сумма квадратов, средний квадрат и величина Фишера: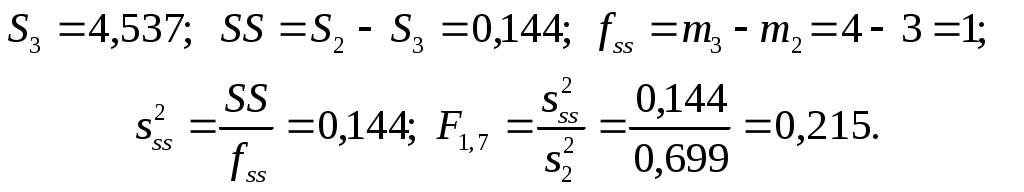



По таблицам распределения (прил. 1) определяем критическое значение Фишера В связи с тем, что полученное из расчета значение критерия Фишера меньше критического, можно считать, что член третьего порядка не добавляет существенной информации и, следовательно, нецелесообразен.


Лабораторная работа № 2