работа. Лабораторная работа 1 (1). Построение моделей идентификации
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
2.3. Статистическая обработка результатов ПФЭ Предположим, что общий вид плана и результаты Таблица 2.1
Рассмотрим последовательность статистической обработки и проверки адекватности построенной модели. 1. Определяются среднее значение 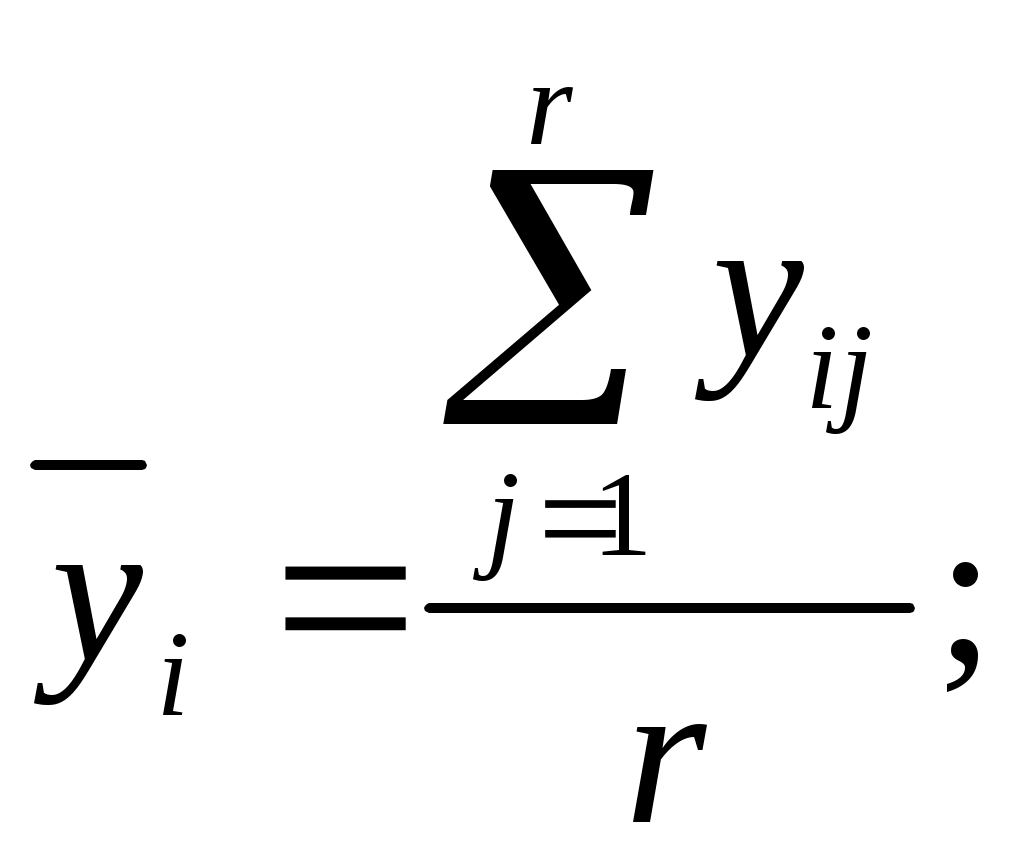 (2.1) (2.1)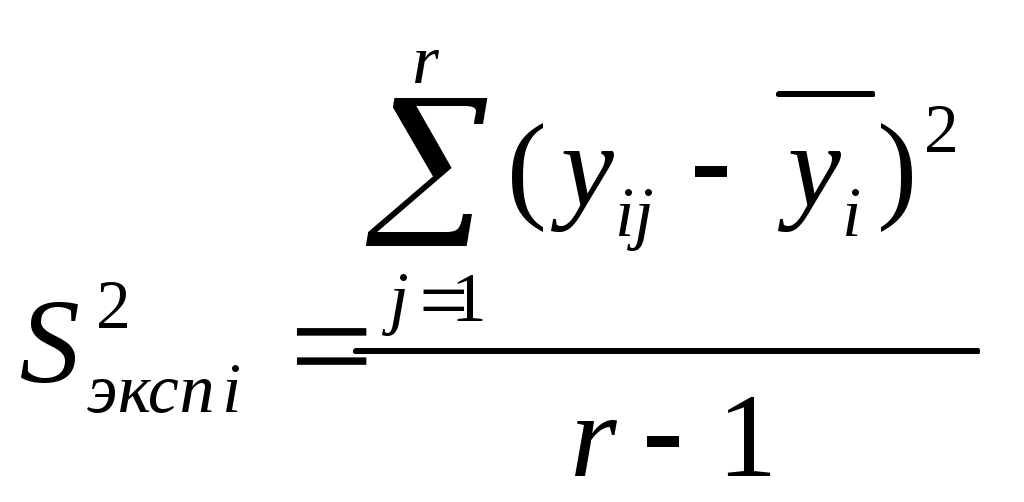 . (2.2) . (2.2) где экспериментов; 2. Выполняется проверка однородности дисперсий 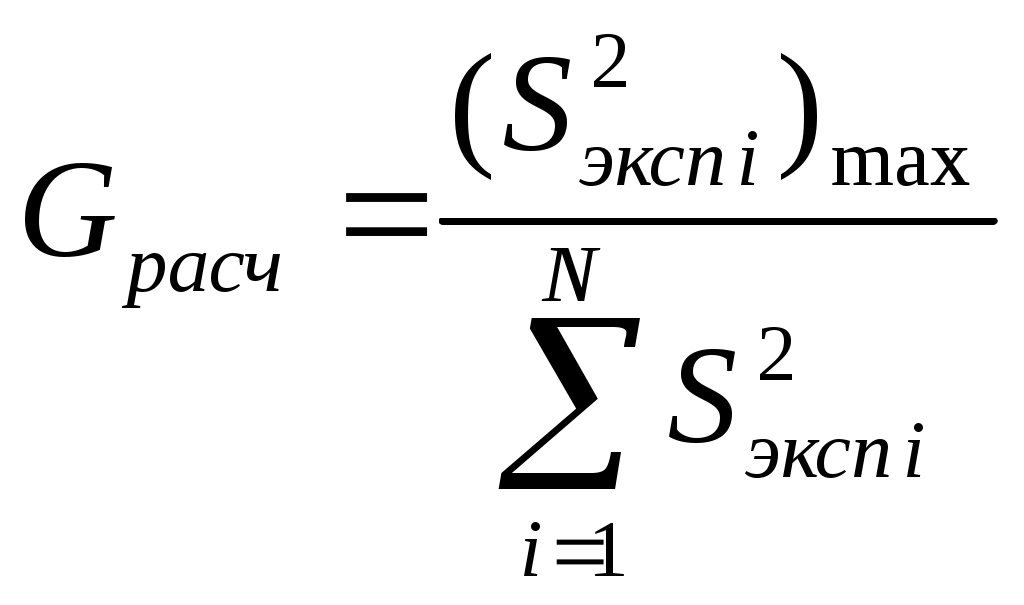 . (2.3) . (2.3)С критерием Проверяется условие где Если условие (2.4) выполняется, то дисперсии однородны и статистическая обработка продолжается. Если не выполняется, то дисперсии неоднородны. В этом случае требуются повторить эксперимент, изменив условия его проведения (набор факторов, интервал их варьирования, точность измерительных приборов и пр.). 3. Определяется оценка дисперсии воспроизводимости экспериментов определяется по формуле 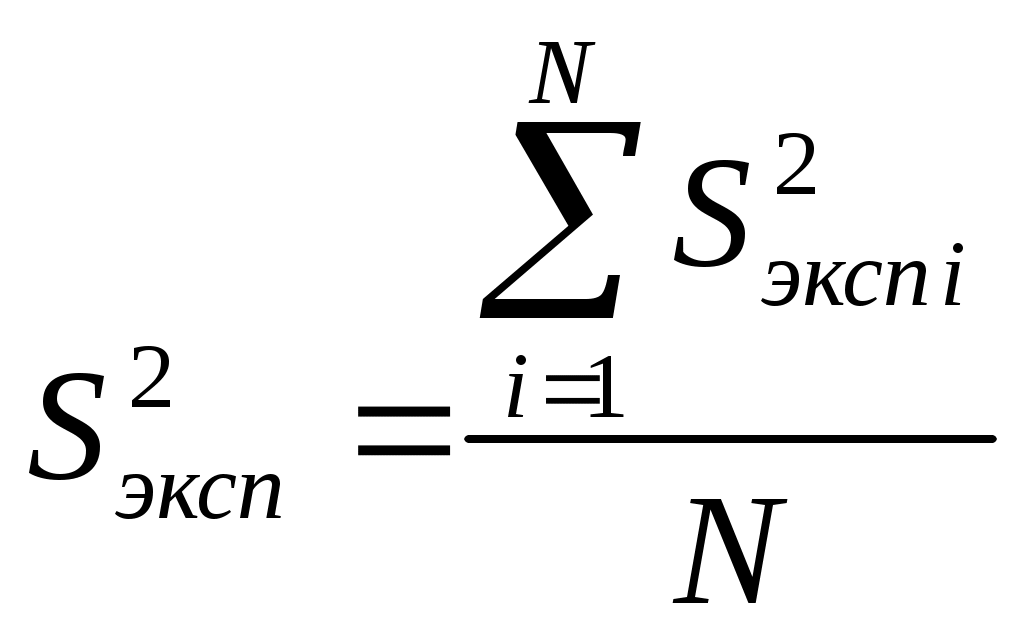 . (2.5) . (2.5)с ней связано число степеней свободы 4. Определяются коэффициенты уравнения регрессии 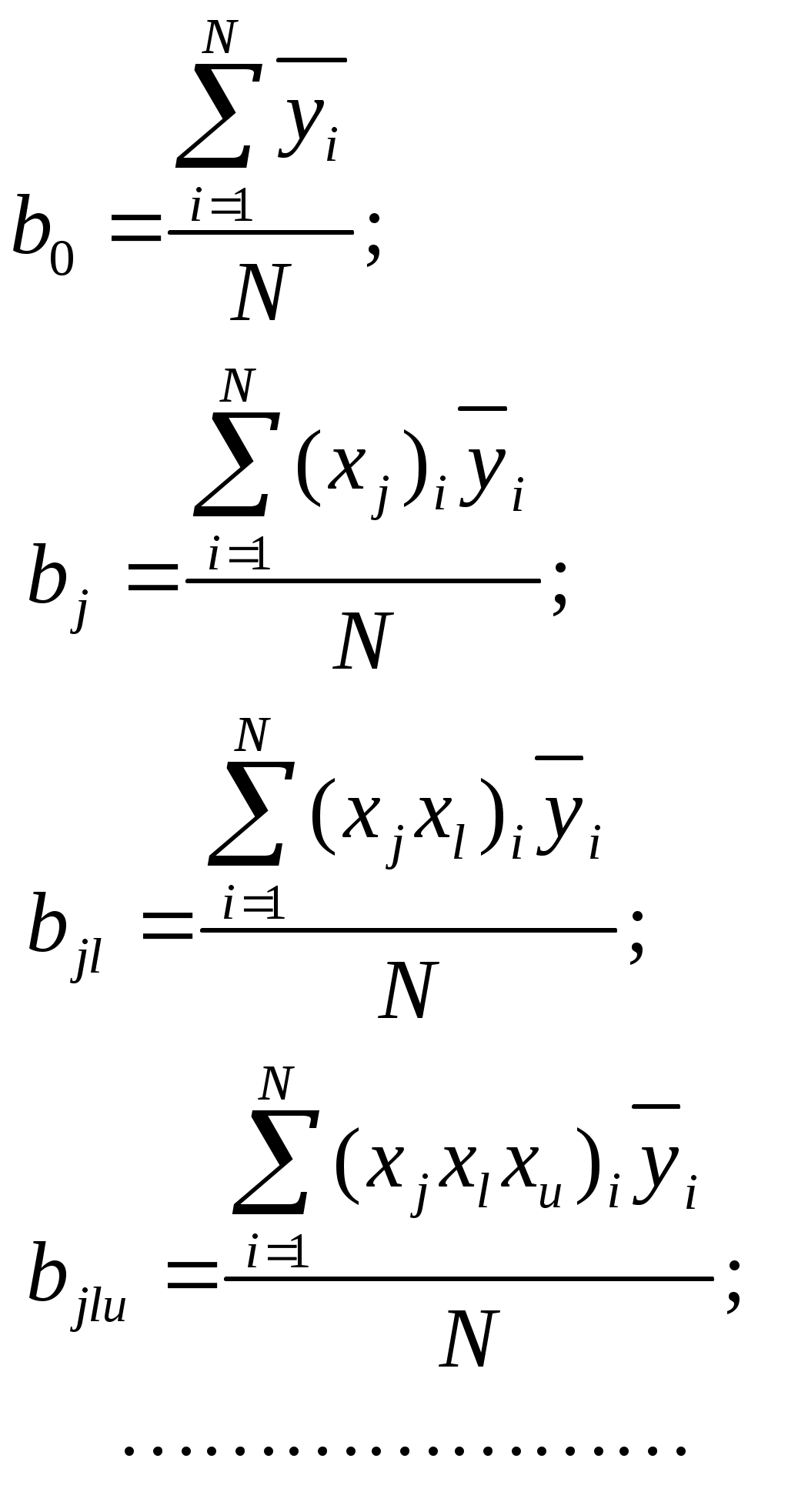 (2.6) (2.6)где матрицы плана; (строке) матрицы плана; эксперименте (строке) матрицы плана. 5. Выполняется проверка значимости коэффициентов уравнения регрессии. Для выполнения проверки нужно построить доверительный интервал где коэффициента его оценкой. Ошибка где вероятности определялась дисперсия Коэффициент (его расчетное значение) значим, если построенный доверительный интервал не содержит точку Если интервал 6. Принимая во внимание только значимые коэффициенты, записывается полином вида 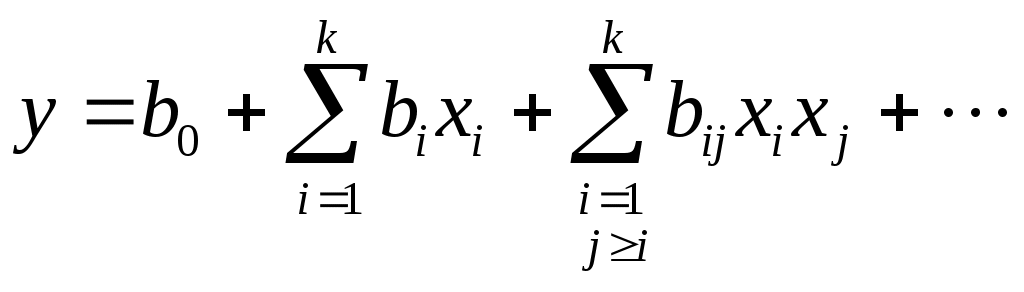 . .Выполняется проверка адекватности модели и делается заключение о ее пригодности для практики. Для этого вначале подсчитывается дисперсия, характеризующая ошибку модели 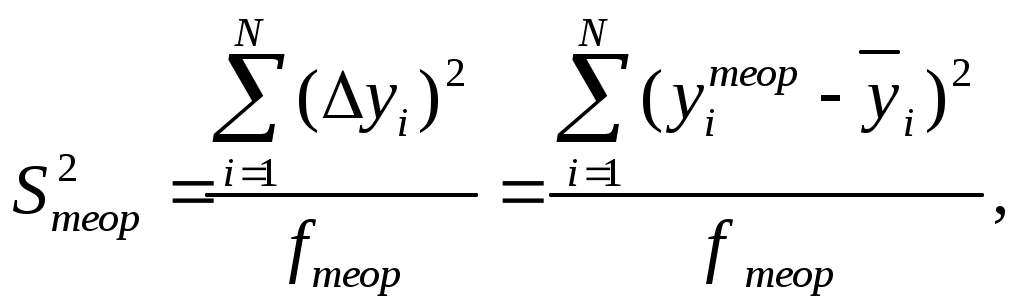 (2.9) (2.9)где (эксперименте); регрессии, кроме коэффициента Затем определяется расчетное значение критерия Фишера С критерием Фишера связанны степени свободы: для числителя Проверяется условие где Если условие (2.11) выполняется, то построенная модель адекватна эксперименту. При невыполнении условия (2.11) модель неадекватна и пользоваться на практике ей нельзя. Для лучшего понимания алгоритма статистической обработки ниже рассмотрим пример. 2.4. Пример выполнения работы Для исследования выходного параметра технологического процесса при числе параметров k=2 был спланирован ПФЭ Таблица 2.2
Требуется построить модель, описывающую выходной параметр технологического процесса, проверить ее адекватность. Эксперимент проводится при двух значениях фактора 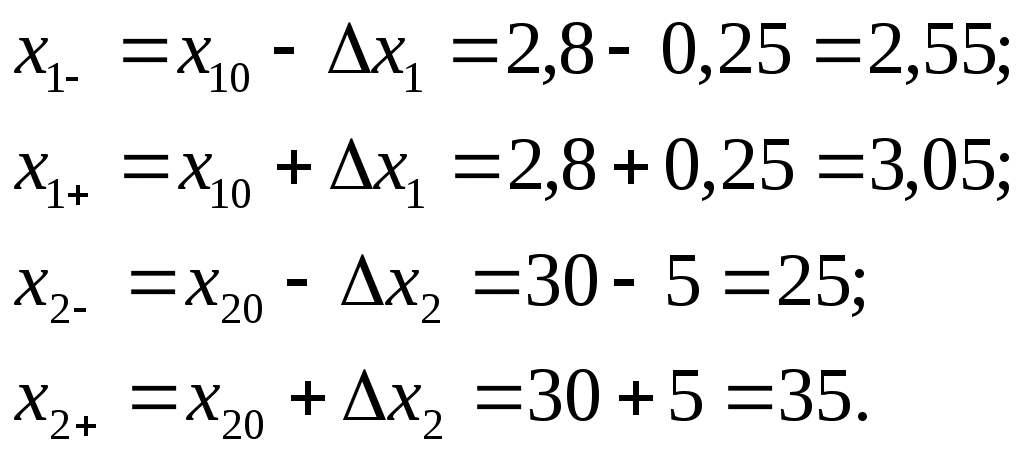 Для облегчения расчетов удобно провести нормировку факторов с помощью преобразований 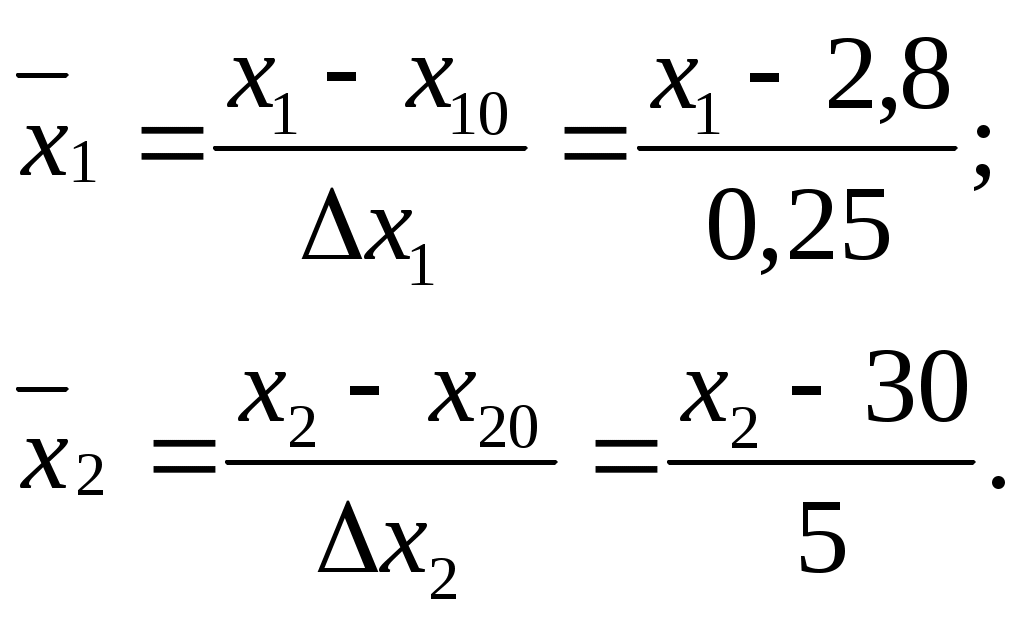 (2.12) (2.12)По формулам (2.1) и (2.2) посчитываем среднее значение и дисперсии в каждом эксперименте матрицы Результаты расчета величин По формуле (2.5) находим дисперсию воспроизводимости опытов 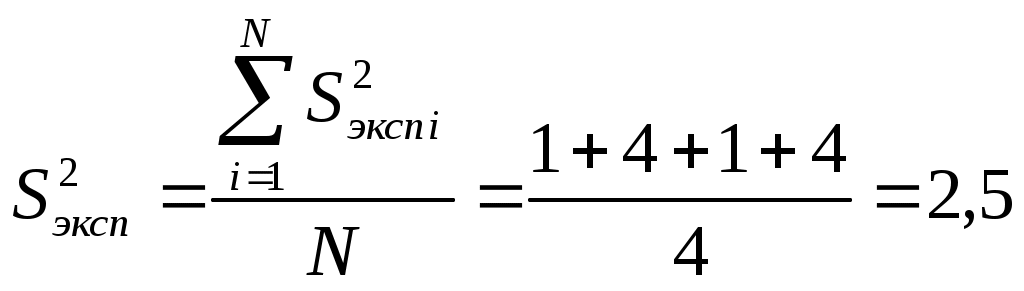 . .Используя формулы (2.6) определим коэффициенты уравнения регрессии: определение свободного члена вычисление коэффициентов уравнения, характеризующих линейные эффекты 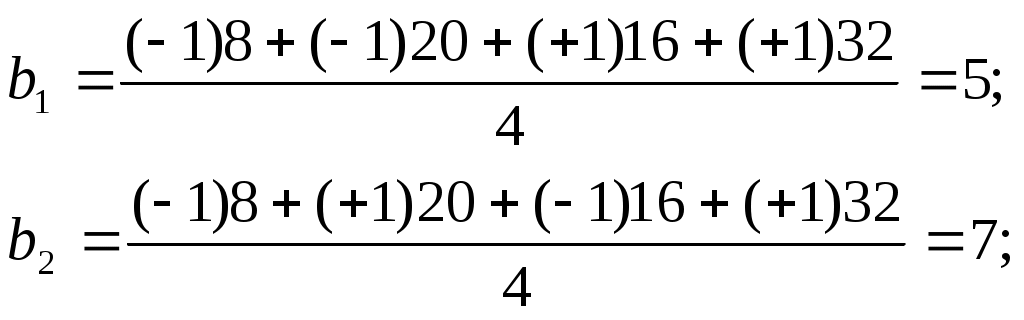 определение коэффициента уравнения, характеризующего эффект взаимодействия Проверяем значимость коэффициентов. По таблицам распределения критерия Стьюдента при находим Определяем Так как выполняются условия то коэффициенты Линейная модель запишется в виде Проверим адекватность этой модели. По формуле (2.9) подсчитаем дисперсию, характеризующую ошибку модели. Для получения значений Аналогично находим Используя формулу (2.9) определяем дисперсию, характеризующую ошибку модели 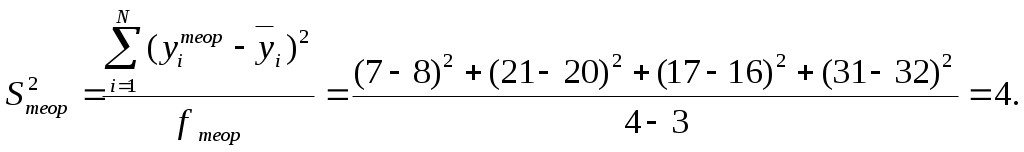 Расчетное значение критерия Фишера находим по выражению (2.10) По таблице критерия Фишера для доверительной вероятности по значениям числа степеней свободы Так как условие (1,6<5,32), то линейная модель вида (2.13) адекватна результатам эксперимента и ею можно пользоваться на практике. Осуществим переход к размерному полиному, используя соотношение (2.12), значения нулевых уровней и интервалов варьирования факторами Получаем | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
