Модели. Построить граф биологической классификации видов. Используя граф, определить, какими признаками будут обладать следующие существа
 Скачать 209.03 Kb. Скачать 209.03 Kb.
|
|
Построить граф биологической классификации видов. Используя граф, определить, какими признаками будут обладать следующие существа.  Класс            морских лилий змеехвосток брюхоногие голотурий двустворчатые       головоногие         кальмар  устрица           голова Горгоны лилия стебельчатая осьминог каракатица теребра виноградная улитка кукумария трепанг мидия морской гребешок  Числительные Представить информацию о классификации в русском языке в виде графа. Является ли полученный граф деревом?     По значению По составу           Количественные Порядковые Составные Сложные Простые                     два шесть девятый второй Сто пятьдесят четыре Тридцать пять четыре пять пятьсот шестьдесят На основании исходных данных постройте аддитивную модель временного ряда
РЕШЕНИЕ Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Аддитивная модель – модель вида: Y=T+S+E, где Т - трендовая компонента; S – циклическая компонента; Е – случайная компонента. Алгоритм построения аддитивной модели. Шаг 1. Выравнивание исходных уровней ряда методом скользящей средней: Суммируем уровни ряда последовательно за каждый промежуток времени, в котором наблюдаются колебания со сдвигом на один момент времени и определяем условные величины показателя Y. 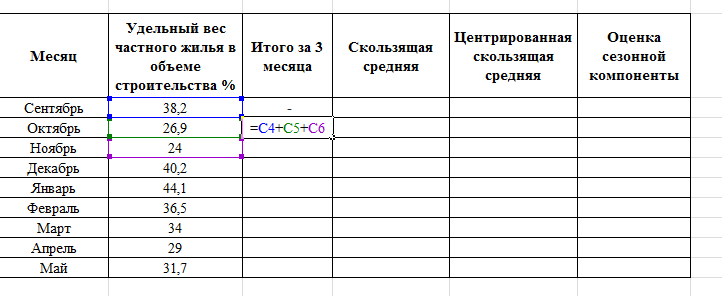 Делим полученные величины на число моментов времени в промежутке и находим скользящие средние. 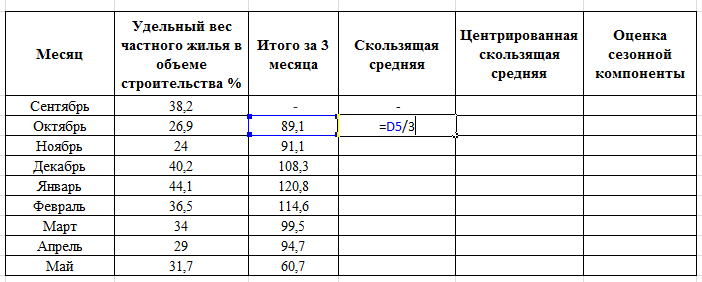 Находим средние значения из двух последовательных скользящих средних – центрированные скользящие средние. 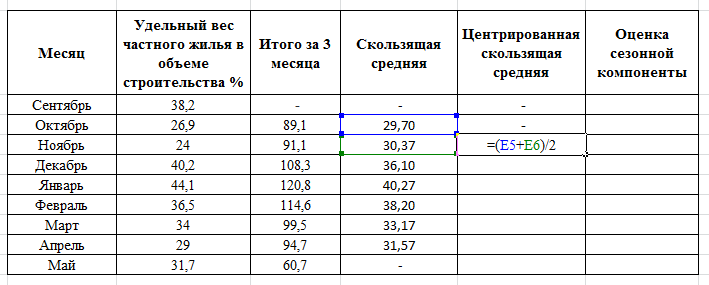 Шаг 2. Оценка сезонной компоненты: Находим оценку сезонной компоненты, как разность между фактическими уровнями ряда и центрированными скользящими средними. 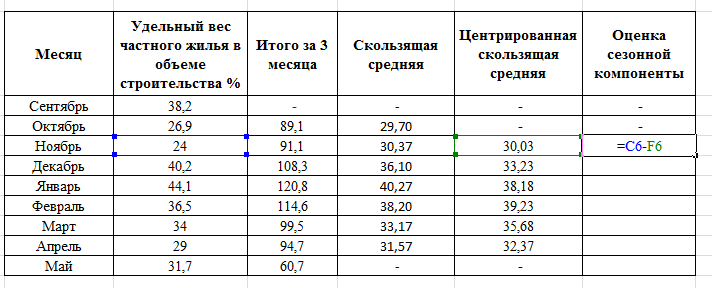 Находим средние оценки сезонной компоненты за каждый промежуток времени, в котором наблюдаются колебания. 3. Исходя из условия взаимопогашения сезонных воздействий определяем корректирующий коэффициент k: в аддитивной модели; где n – период колебаний. 4. Рассчитываем скорректированные значения сезонных компонент: в аддитивной модели: 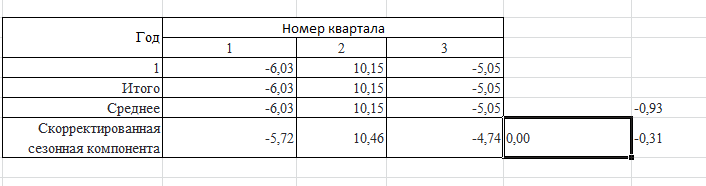 Шаг 3. Элиминирование влияния сезонной компоненты: Находим значения Т+Е как Y-S – в аддитивной модели. Шаг 4. Определение трендовой компоненты ряда. 1. Трендовая компонента ряда определяется с построения регрессионной модели, параметры которой находятся методом наименьших квадратов. 2. С уравнения регрессии находим уровни трендовой компоненты Т для каждого момента времени t. Шаг 6. Находим значения Т+S. Шаг 7. Находим случайную компоненту Е= Y-(T+S) Шаг 8. Оценка качества модели. 1. Находим сумму квадратов случайной компоненты. 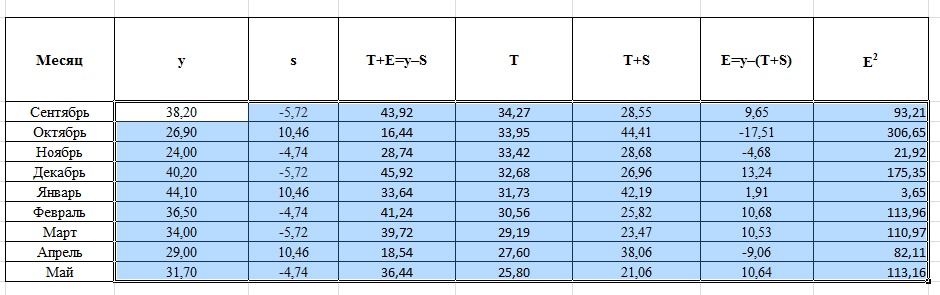 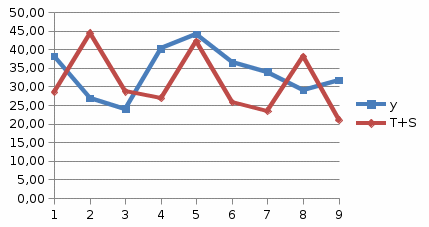 |
