Проект. Итог.. Повышение эффективности уроков математики с помощью прикладных задач
 Скачать 177.84 Kb. Скачать 177.84 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра «Педагогика и психология» Направление подготовки: 44.04.01 Педагогическое образование Магистерская программа: Образовательный менеджмент Проект на тему: «Повышение эффективности уроков математики с помощью прикладных задач» по дисциплине «Педагогическое проектирование» Студент: Казьмин А. В. Курс: 1. Группа: 22ЗНПОм1 Преподаватель: к.п.н., доцент Груздова О. Г. Пенза, 2023 Аннотация проекта Проект «Повышение эффективности уроков математики с помощью практико-ориентированных задач» направлен на решение проблемы реализации новых образовательных стандартов средствами системно – деятельностного подхода. Данный проект позволяет реализовать многие личностные потребности студентов. Он дает студентам возможность применить и нарастить не только свои теоретические знания, но и использовать свой житейский опыт и знания в будущей профессии для дальнейшего развития личности. Тип проекта – практико-ориентированный. Содержание Введение ………………………………………………………………………………….....4 1.Теоретические вопросы темы……………………………………………………….....7 1.1.Задачный подход в практике преподавания математики……………………........7 1.2. Роль практических задач при обучении математики ………………………....…8 2. Методические вопросы темы ………………………………………………………..10 2.1. Построение методики применения практико - ориентированных задач...…..10 2.2. Разработка практико-ориентированных задач …………………………………..11 3. Этапы реализации проекта……………………………………………………..….....14 Заключение……………………………………………………………………………......21 Список литературы и Интернет-ресурсов…………………………………………....22 Приложения…………………………………………………………………………….....23 «Сближение теории с практикой даёт самые благотворные результаты, и не одна только практика от этого выигрывает». Чебышев П. Л. Введение. В ФГОС среднего профессионального образования отмечено, что работник должен обладать системой фундаментальных знаний и навыков, профессиональной компетентностью; быть мобильным в профессиональной среде и конкурентоспособным на мировом рынке труда. Образовательные стандарты отводят особую роль математике как одной из фундаментальных наук, а профессиональная направленность обучения позволяет рассматривать математику, во-первых, как средство, с помощью которого можно спроектировать процесс профильно-ориентированного обучения, во-вторых, как форму специфической межпредметной взаимосвязи общеобразовательных и профессиональных знаний. Будущие рабочие, изучая специальные предметы, постоянно сталкиваются с потребностью в тех или иных математических знаниях. Поэтому математику следует рассматривать как важнейшую составляющую качественной подготовки рабочих и служащих. Это обусловлено не только тем, что математика является важным элементом общей культуры, универсальным языком науки, в целом, но и, главным образом, тем, что она является мощным средством решения прикладных и практико-ориентированных задач. В наш техникум приходят обучающиеся с низкой математической подготовкой, но у многих из них интересы в определенной степени уже сформированы: они направлены на избранную профессию. Поэтому одним из мотивов, стимулирующих интерес к изучению того или иного вопроса курса математики, является его практическая и профессиональная значимость. А этого можно добиться, используя практико-ориентированные задачи при обучении. Но, к сожалению, действующие учебники мало предлагают таких задач. Этим и обусловлена актуальность темы. Прикладная направленность – одно из традиционных направлений в преподавании математики. Исследуя историю вопроса, было обнаружено, что наши студенты, занимая ведущие места среди зарубежных сверстников по качеству и объёму теоретических знаний, в рейтинге резко опускались вниз, если им предлагалось решить жизненную ситуацию. И хотя нынешнее поколение более прагматично, чем предыдущее, существующая система образования такова, что большинство студентов плохо понимает, зачем ему это нужно сейчас и пригодится ли в жизни вообще. Поэтому существует объективная необходимость практической ориентации курса математики. На усиление прикладной направленности обучения математики указано и в стандартах образования. Содержание и структура экзаменационных работ по математике содержат задания, которые требуют овладение математическими знаниями и умениями, необходимыми для применения их в практической деятельности и повседневной жизни. Вместе с тем базовый уровень является недостаточным для реализации данного положения, что и определяет актуальность использования практико-ориентированных задач в учебном курсе математики. Проблема: Ориентируясь на новые образовательные инициативы, в своей деятельности мне пришлось столкнуться с рядом противоречий. Это противоречия между: традиционным обучением и потребностями общества в компетентных личностях; глубокими теоретическими основами курса математики и его практической направленностью; однообразием содержания учебного материала и многообразием форм творческой деятельности студентов на занятиях. Данные противоречия позволили выявить проблему эксперимента. Разрыв между социально обусловленными требованиями общества к выпускнику техникума, выражающимися, в частности, в потребности постоянного совершенствования умений, способности самостоятельно ставить и решать разнообразные задачи профессионального и жизненного плана, и недостаточной разработанностью вопросов использования педагогических систем, обеспечивающих выполнение этих требований. Поэтому цель данного проекта следующая: Цель: Разработка методического вопроса по составлению и применению практико-ориентированных задач при обучении математики. В соответствии с поставленной целью мною решались следующие Задачи: изучить теоретические вопросы по теме исследования; определить роль и место практико – ориентированных задач в учебном процессе разработать практико-ориентированные задачи организовать проектную и исследовательскую деятельность студентов на уроках математики и во внеурочной работе. проверить эффективность внедрения в курс математики прикладных и практико-ориентированных задач. Новизна данного проекта состоит в активных формах обучения, направленных на развитие компетентностей студента с помощью интеграции работы над выработкой определенного стиля математического мышления, внедрением информационных технологий в развитие математической культуры. Объект исследования: процесс формирования определенного стиля математического мышления в условиях реализации педагогического принципа связи теории с практикой. Предмет исследования: методические основы организации обучения на уроках математики. Методы исследования: анализ федеральных государственных образовательных стандартов, изучение и обобщение педагогического опыта, анализ имеющейся литературы, программно-методической документации, индивидуальных разработок по изучаемой проблеме; анкетирование, сравнение результатов контрольных работ. Гипотеза: Если использовать практические задачи в курсе математики, то это будет способствовать формированию универсальных учебных действий и положительно влиять на динамику познавательной деятельности студентов По завершению работы ожидаются следующие результаты: Ожидаемые результаты сформированность у обучающихся устойчивой мотивации к деятельности; повышение качественного показателя обучения и эффективности урока рост числа обучающихся, занимающихся исследовательской деятельностью; переход от информационной, «знаниевой» образовательной модели урока к деятельностно – компетентностной; совершенствование собственной профессиональной деятельности; 1.Теоретические вопросы темы. 1.1.Задачный подход в практике преподавания математики. Для человека чрезвычайно важно не столько энциклопедическая грамотность, сколько способность применять знания и умения для разрешения конкретных ситуаций и проблем, возникающих в реальной действительности. По мнению психолога В. В. Давыдова и методистов - математиков Д.Пойа, Л.М.Фридмана, Г.И.Саранцева, Т.А.Ивановой [3], формировать способность разрешения проблем помогают специальным образом подобранные практико-ориентированные задачи. Практика показывает, что студенты с интересом решают и воспринимают задачи практического содержания. Однако в учебниках математики таких задач почти нет. Да и в методических пособиях практико-ориентированные задачи встречаются редко. Подбор задач, формирующих элементарные навыки приложения математики, дело не простое. Многие из текстовых задач в учебниках неестественны с прикладных позиций. Поиск и систематизация поучительных и в то же время достаточно простых задач подобного рода – весьма актуальная проблема. Решение практико-ориентированных задач тогда эффективно, когда студенты встречались с описываемой ситуацией в реальной действительности: в быту, на экскурсии, при изучении других предметов. Эффективным средством является широкое использование наглядности: фотографий, слайдов, плакатов, рисунков и т.д. Такие задачи повышают интерес студентов к самому предмету, поскольку для подавляющего большинства ценность математического образования состоит в ее практических возможностях. Под задачей с практическим содержанием понимается математическая задача, которая раскрывает приложения математики в окружающей нас действительности, в будущей профессии, в смежных дисциплинах, знакомит ее с использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту. Важным средством достижения прикладной и практической направленности обучения математике служит планомерное развитие у студентов наиболее ценных для повседневной деятельности навыков выполнения вычислений и измерений, построения и чтения графиков, составления и применения таблиц, пользование справочной литературой. Возможны различные пути формирования подобных навыков. В этой связи являются перспективными вычислительные практикумы, лабораторные работы по измерению геометрических величин, измерительные работы на местности, задания на конструирование и преобразование графиков. Задачи с практическим содержанием целесообразно использовать в процессе обучения для раскрытия многообразия применения математики в жизни, своеобразия отражения ею реального мира и достижения дидактических целей таких, как: мотивация введения новых математических понятий и методов; иллюстрация учебного материала; закрепление и углубление знаний по предмету; формирование практических умений и навыков. 1.2. Роль практических задач при обучении математики. Часто уроки математики не дают убедительного ответа на вопрос «зачем все это нужно?» Здесь должна решаться важная методическая проблема сближения методов решения задач с методами, применяемыми на практике; необходимо раскрытие особенностей прикладной математики, ее воспитательных функций; усиливать межпредметные связи. Необходимо на доступном для студентов языке обеспечивать действительные взаимосвязи содержания математики с окружающим миром, рекомендовать применение отдельных тем в смежных науках, в профессиональной деятельности, в производстве, в быту. Роль и значение математики в развитии межпредметных связей и формировании у обучающихся навыков практической деятельности рассматриваются в работах М.Б. Балка, Б.В. Гнеденко, В.А. Гусева, А.Г. Мордковича, А.В. Усовой и других[2]. Анализ работ перечисленных авторов позволяет сделать вывод о том, что эта связь осуществляется за счет прикладной направленности математики. При этом основным носителем такой направленности являются практико-ориентированные задачи (Е.В. Величко, И.М. Шапиро и др.).[6] Именно поэтому межпредметные связи являются важным условием и результатом комплексного подхода в обучении студентов. Привлечение межпредметных связей повышает научность обучения, доступность (теория насыщается практическим содержанием), необходимо включать в урок элементы занимательности. Однако появляется и немало трудностей: преподавателю требуется освоить другие предметы, практическая задача обычно требует больше времени, чем теоретическая, возникают вопросы увязки программ и другие. О многообразии использования математики во всех сферах человеческой жизнедеятельности говорят следующие высказывания великих: «Математика – это язык, на котором написана книга природы» (Г. Галилей). «Полет – это математика» (В. Чкалов). «Вдохновение нужно в геометрии, не меньше, чем в поэзии» (А.С. Пушкин). «Химия – правая рука физики, математика – ее глаз» (М.В. Ломоносов). Для формирования интереса к изучению предмета следует создавать производственные проблемные ситуации, которые решаются при помощи математических знаний и умений. Изучение сложного математического материала становится более интересным, если студенты видят практическое применение изучаемых тем непосредственно в своей профессиональной деятельности. Решение задач с производственной направленностью способствует формированию у студентов способностей находить в профессиональной ситуации существенные признаки математического понятия, подводить объект под математическое понятие, использовать его в новых условиях. В процессе решения предусматривается совершенствование рационального применения теоретических знаний к решению практических задач, развития пространственного воображения и вычислительных навыков, организации самостоятельной работы с измерительными приборами, таблицами, справочной литературой. Видение возможности реализации приобретаемых знаний способствует развитию мотивации к обучению и достижению успеха. Таким образом, решение задач профессионального характера на уроках способствует развитию интереса к математике как к науке и как к профессионально значимой дисциплине, показывает прикладной, реально ощутимый характер математики. Студенты понимают, что математика – важный предмет в их образовании. Любая конструкция, любой технологический процесс требует расчетов, порой содержащих больше математики, чем техники. 2. Методические вопросы темы. 2.1. Построения методики применения практико-ориентированных задач. Профессионально значимые знания и умения являются основой построения методики применения практико-ориентированных задач. Задачи с профессиональной направленностью создаются на основе тех знаний и умений по математике, которые непосредственно или опосредованно связаны с профессиональными знаниями и умениями. В учебном заведении за ними закрепилось название профессионально значимых. Одним из главных условий построения методики применения задач по математике с профессиональной направленностью является отбор совокупности этих знаний и умений. Решение задач профессионального отбора следует начинать с понимания того, какие именно требования предъявляются к человеку данной профессии, какими видами деятельности ему предстоит овладеть. Профессионально значимые знания и умения по математике могут применяться в «готовом виде» для формирования на их основе профессиональных умений и навыков, теоретического обоснования практических действий и т.д. Эти знания помогают осмыслить сущность той или иной производственной операции; понять принципы устройства и действия орудий труда, справедливость требования безопасности труда. Существуют профессионально значимые математические знания, которые первоначально вводятся, а затем формируются не только на уроках математики, но и на уроках других предметов естественно - математического цикла (физике, географии и т.д.). Они служат для лучшего осознания обучающимися производственных процессов, операций, для повышения их профессиональной грамотности. Ряд профессионально значимых знаний и умений могут первоначально формироваться на предметах профессионально-технического цикла, затем обогащаться и уточняться на уроках математики. Профессионально значимые математические знания и умения могут первоначально вводится на уроках математики, а формироваться и применяться на уроках математики, профессиональных дисциплинах и производственном обучении. Таким образом, применение задач с профессиональной направленностью требует выявления признаков профессионально значимых знаний и умений, а также отбора (согласно этим признакам и требованиям к отбору) совокупности знаний и умений из курса математики, значимых для данной профессии. Установление этапов межпредметного и межциклового формирования выделенных знаний подтвердило положение о необходимости соблюдения преемственности в процессе их изучения и обозначило место введения дидактических материалов с профессиональной направленностью в структуре урока, а именно при актуализации основных знаний и умений, формировании и закреплении новых понятий и способов действий. 2.2. Разработка практико-ориентированных задач. Практика показывает, что студенты с интересом решают и воспринимают задачи практического содержания. К задаче следует предъявлять следующие требования: задачи должны соответствовать программе курса, вводиться в процесс обучения как необходимый компонент, служить достижению цели обучения; вводимые в задачу понятия, термины должны быть доступными для студентов, содержание и требование задачи должны «сближаться с реальной действительностью»; способы и методы решения задачи должны быть приближены к практическим приемам и методам; прикладная часть задачи не должна покрывать ее математическую сущность; текст задачи должен отражать реализацию межцикловых и межпредметных связей. Практико-ориентированные задачи могут быть использованы с разной дидактической целью: они могут заинтересовать или мотивировать, развивать умственную деятельность, формировать практические умения и навыки, объяснять соотношение между математикой и другими дисциплинами. Решение задач с практическим содержанием могут быть предложены учащимся на различных этапах обучения. Решение задач на этапах восприятия и осмысления нового материала имеет целью пробудить у студентов потребность в расширении знаний, познавательный интерес и научить их методам самостоятельного приобретения знаний. Решая и анализируя задачи на этапах закрепления и повторения учебного материала, учащиеся овладевают способами применения знаний на практике и вместе с тем более глубоко усваивают его содержание. При проверке усвоения программного материала решение задач с производственным содержанием позволяет установить, насколько прочно и глубоко его усвоили. Решение всех задач проходит в четыре этапа. 1.Анализ условия задачи. Задача формулируется на описательном языке. От правильной постановки задачи, указания ресурсов, которыми мы располагаем, зависит успешность ее решения. Этому нужно учиться каждому так как пригодится специалисту любого профиля. 2.Построение математической модели задачи. Перевод исходной задачи на математический язык: вводятся переменные, ищутся связи между ними и устанавливаются ограничения на них, которые записываются в виде уравнений, неравенств или их систем. Любая математическая задача — модель каких-то прикладных задач (экономических, физических, биологических, технических и т.п.). 3. Решение математической модели задачи. Изучается полученная модель. Если задача известная, то она решается по соответствующему ей алгоритму. Если задача никогда не решалась, то ищется необходимый алгоритм. 4.Интерпретация решения. Это перевод решения задачи на исходный язык. Рассмотрим пример практико-ориентированной задачи. Например, задачу связанную с конусом. Сначала обсуждается одна из ситуаций, в которой фигурирует объект, имеющий форму конуса (это куча зерна), ищется решение проблемы измерения необходимых для решения задачи величин.  Задача. Найти объем кучи зерна. — Будем считать, что куча зерна имеет форму конуса. Какие элементы конуса необходимо знать, чтобы вычислить искомые величины? (Радиус основания, длину образующей и высоту конуса). — Высоту и радиус основания невозможно найти непосредственным измерением. Как найти радиус основания в этом случае? (Пусть у нас имеется, например, мягкая метровая лента. Измерим ею длину окружности основания кучи зерна и разделим это число на 2π). — Каким образом можно измерить длину образующей?( Перекинув метровую ленту через вершину кучи, мы определим длину двух образующих. Разделим ее на 2). — Осталось определить высоту кучи зерна. (Зная радиус и длину образующей, вычислим по теореме Пифагора высоту кучи зерна). — Теперь мы можем вычислить площадь поверхности и объем кучи зерна. После измерения получили: длина окружности кучи зерна равна 7,2 м. Длина двух образующих — 2,6 м. Найдите объем этой кучи, считая π = 3. — Вычислим радиус основания конуса: Длина одной образующей равна 1,3 м. Высоту конуса вычислим по теореме Пифагора Тогда Далее можно предложить вычислить массу зерна. Итак, задачи с профессиональной направленностью служат средством управления познавательной деятельностью обучающихся. Они применяются на любом из этапов процесса формирования профессионально значимых математических понятий и теоретических утверждений: могут быть задействованы на уроке до, после и одновременно с введением новых знаний. 3. Этапы реализации проекта. 3.1.На подготовительном этапе были проведены. Анализ федеральных государственных образовательных стандартов, изучение и обобщение педагогического опыта, анализ имеющейся литературы, программно-методической документации, учебных планов, индивидуальных разработок. Разработка дидактических материалов В результате были определены основные параметры исследования, проблема, его предмет, методы. 3.2. В период организационно-практического этапа выявлялись и систематизировались педагогические условия для реализации проекта, создавалась программа обучающего эксперимента; осуществлялась проверка гипотезы и обобщение полученных экспериментальных данных, их математическая обработка. Так были проведены анкетирование студентов, различные диагностики с целью выявления уровня познавательного интереса и мотивации обучения, входные проверочные работы, в которые были включены не только задачи, решаемые с помощью математического моделирования, но и занимательные задачи, и задачи на решение жизненных ситуаций, практико-ориентированных задач. Таблица 1 Мотивация деятельности студентов на уроке
Диаграмма 1 Мотивация деятельности студентов на уроке 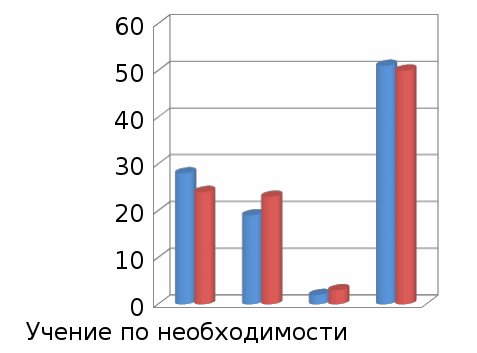 Таблица 2 Результаты контрольных работ на 1 курсе
Диаграмма 2 Результаты контрольных работ на 1 курсе 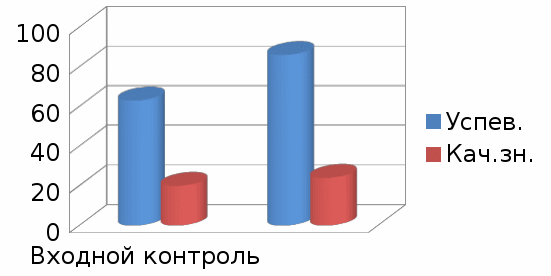 Были составлены задачи с профессиональной направленностью и другие практико-ориентированные задачи (Приложения 1-3) 3.3.Обобщающе-практический этап. Анализ, систематизация и обобщение исследования были осуществлены на обобщающе-практическом этапе. Также были сформулированы выводы и завершено оформление педагогического проекта Пути решения Для проверки гипотезы были намечены пути решения проблем через Использование в процессе обучения прикладных задач; Выполнение практических и лабораторных работ; Разработка и проведение интегрированных уроков, практикумов, семинаров и т.д.; Использование современных педагогических технологий: ИКТ, метод проектов, проблемное обучение модельный метод обучения (занятия в виде деловых игр и др.) Подготовка сообщений о методах использования математического аппарата в разных науках и в производственной сфере Следует отметить, что повышение эффективности уроков и уровня познавательной активности невозможно без различных видов и форм внеурочной деятельности, таких как олимпиады, конкурсы, предметные декады, проектная деятельность, экскурсии. В работе над проблемой исследования использовались информационно-коммуникативные технологии. Результативность: В результате Проанализировано состояние проблемы исследования в психолого – педагогической и научно – методической литературе. Экспериментально проверены результаты внедрения в курс математики практико-ориентированных задач. Разработаны дидактические материалы для учебного процесса и внеурочной работы с применением практических задач Совместно со студентами разработаны проекты: «Математика в военном деле», «О вреде наркотиков – языком математики», «Экологические проблемы и математика» и др. За последние два года несколько возросло качество знаний по математике, уровень познавательного интереса и мотивации деятельности студентов. УМК дополнен теоретической частью, разработками уроков, внеурочных мероприятий и т. д., и практической частью: набором практических, прикладных и занимательных задач. Повысилось количество студентов, занимающихся проектной и исследовательской работой, возросла активность участия в олимпиадах, конкурсах, во внеурочных мероприятиях. За время работы над проектом происходило совершенствование собственной профессиональной деятельности. В ходе реализации проекта было принято участие в проведении семинаров , методических дней, недель, в научно-практических конференциях, педагогических чтениях на базе техникума. На основании выше сказанного можно сделать следующие выводы: Использование практических задач в курсе математики: 1. Повышает эффективность уроков, что ведёт к повышению качества знаний 2. Способствует положительной динамике познавательной деятельности студентов 3. Решает задачу социализации личности студента А это частично разрешает существующие противоречия и доказывает правильность выдвинутой нами гипотезы о том, что Использование практических задач в курсе математики способствует формированию универсальных учебных действий и ведет к реальному повышению уровня качества обучения. Таким образом, следует считать, что гипотеза исследования подтвердилась. Заключение. Практика показала, что систематическая работа по решению и конструированию практико-ориентированных задач и использование разнообразных приёмов дает положительные результаты. Изучение сложного математического материала становится более интересным, так как студенты видят практическое применение изучаемых тем непосредственно в своей профессиональной деятельности и в жизненных ситуациях. Рано или поздно всякая правильная математическая идея находила применение в том или ином дее. Крылов А.Н. В заданиях показывается студентам значимость математических знаний для их профессии, что ориентирует их на новый, более высокий уровень изучения математики. Систематическое использование на уроках задач профессиональной направленности является связующей нитью между теорией и практической деятельностью, что способствует более глубокому освоению профессии, способствует развитию интереса к математике как к науке и как к профессионально значимой дисциплине, показывает прикладной, реально ощутимый характер математики. Студенты понимают, что математика – важный предмет в СПО. Методик использования практико-ориентированных задач и их составления при обучении математике разработано недостаточно. Поэтому необходимо составлять такие задачи и определять их место на уроках математики. Решение задач с практическим содержанием – одна из важных форм работы по осуществлению профессиональной направленности преподавания математики в средних профессиональных учреждениях, которую необходимо более активно использовать при проведении уроков и организации внеурочной работы. Список литературы и Интернет-ресурсов. 1. Апанасов П.Т., Апанасов Н.П. Сборник математических задач с практическим содержанием. М.Просвещение,1987. 2.Гусаков В.Я. Сборник задач по математике для подготовки рабочих профессий.М.:Высш.шк.,1984. 3.Данилова М.И. Применение математики к решению прикладных задач. М.Ш., 1981. 4.Колягин Ю.М. О прикладной и практической направленности обучения математике. М.Ш., 1985. 5.Сухорукова Е.В. Прикладные задачи как средство формирования математического мышления учащихся. М., 1997. 6.Шапиро И.М. Использование задач с практическим содержанием в преподавании математики. М.: Просвещение, – 1990. 7.Тихонов А.Н., Костомаров Д.П. Рассказы о прикладной математике. М.: Наука. – 1974. Всероссийский Интернет-педсовет. http:// pedsovet.org Единая коллекция Цифровых Образовательных Ресурсов http:// school-collection.edu.ru Информационный образовательный портал. http://www.openclass.ru Профессиональное сообщество педагогов. http://metodisty.ru http://www.math-on-line.com – Занимательная математика школьникам (олимпиады, игры, конкурсы по математике) http://www. exponenta.ru – Образовательный математический сайт Приложение 1 Примеры задач с профессиональной направленностью по профессии «Тракторист-машинист с/х производства» Тема: «Перпендикулярность прямой и плоскости» Задача №1 Как проверить, вертикален ли шток поршня в цилиндре двигателя внутреннего сгорания к плоскости тарелки поршня? 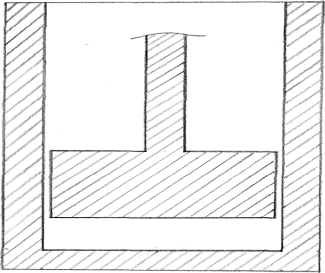 Тема: «Цилиндр» Задача №2 Втулка сепаратора грузового устройства имеет форму цилиндра, высверленного по оси. Внешний диаметр втулки 20 мм, диаметр отверстия 12 мм, длина втулки 100 мм. Найдите площадь диагонального сечения втулки. Задача №3 Вычислите полную поверхность клапана двигателя внутреннего сгорания ЯМЗ - 236, если высота его цилиндрической части 30 мм, высота всего клапана 45 мм, диаметр цилиндрической части 1 0 мм, диаметр тарелки клапана 30 мм. Задача №4 Найти площадь поверхности, которую нужно очистить при ремонте реакционного котла цилиндрической формы, если длина котла 8 м., а диаметр 3,5м. Тема: «Объем цилиндра» Задача № 5 Чему равен суммарный рабочий объем в дм3 10 цилиндров двигателя ЯМЗ - 740 (КамАЗ), если диаметр одного цилиндра 120 мм., ход поршня 120 мм? Задача № 6 Подсчитайте суммарный рабочий объем в дм3 6 цилиндров двигателя ЯМЗ- 236, если диаметр цилиндра 130 мм, ход поршня 140 мм? Задача №7 Найдите объем камеры сгорания двигателя автомобиля КРАЗ, если диаметр поршня 100 мм., ход поршня 150 мм? Задача №8 На сколько увеличится объем камеры сгорания двигателя автомобиля ГАЗ -53, если диаметр поршня 10 см., ход поршня 9 см? Тема: «Многогранники» Задача №9 Размеры кузовов самосвалов МАЗ — 205 и КРАЗ соответственно равны (м): 6,07x2,64x2,44 ; 6,72x2,39x2,18 Какой из них более вместителен? Задача № 10 Требуется отшабрить боковые грани штока, имеющего форму призмы, в основании которой лежит прямоугольник 12x16 мм. Какой длины должен быть шток, чтобы площадь отшабренной поверхности была 450 мм2? Приложение 2 Примеры задач с профессиональной направленностью по профессии «Повар, кондитер» 1.При снятии фактических остатков оказалось 31,2 кг говядины тушеной крупным куском. Определите, сколько говядины было израсходовано, если потери при тепловой обработке составляют 40%, а отходы при холодной обработке 26 %. 2.Тушеной говядины = 31,2 кг. Потери при тепловой обработке - 40%,отходы при холодной обработке - 26 %.Масса израсходованной говядины - ? 3.Рассчитать среднюю цену одного апельсина, если при взвешивании четырех партий по 1 кг оказалось 9, 9, 10 и 12 шт. Цена за 1 кг: 60р. 4. Для приготовления блюд нужно израсходовать 180 кг очищенного картофеля. Сколько неочищенного картофеля следует взять, если отходы при холодной обработке составляют 40% от массы брутто? 5.При разделке говяжьих туш I категории установлены следующие нормы выхода: спинной и поясничной части – 3,5%; заднетазовой – 16,5 %; лопаточной и подлопаточной – 6,5%; грудинки и покромки – 4,5%; котлетное мясо – 43%; отходы и потери – 26%. Определите выход частей туши, если масса составляет 500 кг. 6.Повару необходимо приготовить 13 порций бифштекса по 200 г в каждой. Сколько необходимо взять мяса, если известно, что мясо при варке теряет 35% своей массы? 7.Высота стопки блинов – цилиндра 10см, найдите площадь поверхности блинов, если блины выпекались на сковороде, радиус которой 7 см. 8.Сколько понадобится глазури для оформления боковой поверхности торта цилиндрической формы, если известна высота торта - 15 см, площадь коржа составляет - 169П см2, зная, что на 1см2 пойдет 10 граммов глазури. 9. Сколько понадобится крема для обработки поверхности торта высотой 6 см, составленного из двух коржей, одинаковой толщины, если известно, что площадь поверхности верхнего коржа составляет 144см2 , а площадь поверхности нижнего коржа в 2 раза меньше площади поверхности верхнего коржа. (На 1 см2 расходуется 15 граммов крема.) 10. Повару необходимо приготовить 13 порций бифштекса по 200 г в каждой. Сколько необходимо взять мяса, если известно, что мясо при варке теряет 35% своей массы? 11. Студент насыпал в цилиндрическую кастрюлю немного пшена и спросил соседку: «Сколько нужно налить воды чтобы получилась вкусная каша? –« Это очень просто, - ответила соседка. - Наклони кастрюлю, постучи, чтобы крупа пересыпалась и закрыла ровно половину дна. Теперь заметь точку на стенке кастрюли у края, до которого поднялась крупа, зажми ее пальцем. До этого уровня надо налить воду!»- «Так ведь пшена можно насыпать побольше или поменьше, да и кастрюли бывают разные- широкие, узкие»,- усомнился студент. «Все равно, мой способ годиться в любом случае»,- гордо ответила соседка. Докажите, что соседка права : отношение объемов воды и крупы по ее рецепту для любой цилиндрической кастрюли получается одинаковым. Найдите это отношение. Приложение 3 Примеры различных практико-ориентированных задач. 1. Рассчитайте расход масляной краски, идущей на окраску панели помещения (высота 3м, ширина 4м, длина 5м, высота панели 2,2м), если на окраску 1м2 требуется 0,2 кг (окна и двери занимают 12% площади поверхности). 2. Сколько часов потребуется маляру для окраски панели высотой 2м в помещении (высота 2,7 м, ширина 2,4 м, длина 5 м) маховой кистью или валиком, если норма времени для окраски 100 м2 поверхности: кистью –6,4 часа, валиком – 3,4 часа. К данной задаче можно предложить чертеж помещения. 3. Вычислите вместимость сарая прямоугольной формы с двускатной крышей и прямым углом между стропилами. Размеры сарая: длина – 10 метров, ширина 7 метров, высота стен до крыши 3,5 метра, высота от основания до конька крыши 8,5 метра 4. В магазине имеется два вида парников: один в форме прямоугольного параллелепипеда, другой– в форме полуцилиндра. Определить, какой из них более экономичен по расходу пленочного материала на покрытие, если полезная площадь парников одинакова и равна 10х8 м2, а высота каждого 2м. 5.Семья получила от двух банков ссуду на приобретение квартиры в размере 800 000 руб.: от одного – под 6%, а от другого под 8% годовых. Всего за год они должны уплатить 54600 руб. процентных денег. Сколько денег взято у каждого банка? В урожайное время года (осенью) цены на овощи понизились в среднем на 35%, а к зиме они повысились на 15% по сравнению с прошлогодними ценами. На сколько процентов подорожали овощи по сравнению с осенью? Апельсины подорожали на 25%.Сколько апельсинов можно теперь купить на те же деньги, на которые раньше покупали 4,5кг? Длина комнаты 7м 60см ,а ширина 6м. Сколько рулонов обоев потребуется для оклейки, если длина рулона 10м при ширине 50см. В 2016 году сумма, затраченная на питание в дороге, составила 9700 рублей. Вычислите сумму, которая будет затрачена в 2017 году, если известно, что продукты подорожали на 6%? Чтобы получить суточную норму белков, студенту необходимо съедать в день 0,2кг мяса. Сколько килограммов мяса необходимо съедать в год для нормального развития? Во сколько раз вес съеденного превышает вес среднего студента, если он весит 60кг? Содержание фтора в одной чашке чая относится к суточной потребности человека во фторе, как 2:17. Сколько процентов суточной дозы фтора содержится в одной чашке чая? Сколько чашек чая надо выпить, чтобы обеспечить свой организм фтором? За три зимних месяца в техникуме переболело гриппом 25%студентов. Если в следующем году студентам сделать прививку против этой болезни, то количество заболевших уменьшится на 15%.Сколько студентов не заболеет, если в техникуме учится 600 человек? У помидор первые плоды созревают на 110 день после посева. Когда были посеяны помидоры, если первые зрелые плоды были 5 августа? На 1 кв.м. должно быть 12 растений кукурузы. Сколько растений кукурузы должно быть на 1 гектар? Миша за 3 часа может вскопать 0,2 огорода, а его отец за это же время – 0,7 огорода. Какую часть огорода могут вскопать Миша с отцом за 1 час совместной работы? |
