Информатика. Позиционные системы счисления. Десятичная, двоичная, восьмеричная, шестнадцатеричная системы счисления

Название	Позиционные системы счисления. Десятичная, двоичная, восьмеричная, шестнадцатеричная системы счисления
Анкор	Информатика.docx
Дата	14.03.2019
Размер	179.82 Kb.
Формат файла
Имя файла	Информатика.docx
Тип	Документы #25748

Позиционные системы счисления.

Десятичная, двоичная, восьмеричная, шестнадцатеричная системы счисления.

Позиционная систе́ма счисле́ния (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).

Разряд числа.

Разряд (позиция, место) — это структурный элемент представления чисел в позиционных системах счисления.

Разряд является «рабочим местом» цифры в числе. Порядковому номеру разряда соответствует его вес — множитель, на который надо умножить значение разряда в данной системе счисления.

Диапазон значений для всех разрядов (в данной системе счисления) неизменен.

Основание системы.

Основание позиционной системы счисления это количество различных знаков или символов, используемых для изображения цифр в данной системе

Алфавит цифр.

Алфавит цифровой, совокупность графем (от греческого gràphō - пишу) данной системы записи чисел. Для десятичной системы каждый графем при начертании составляет определенную весовую долю от основания десятичной системы (десяти), равную порядковому номеру графема. Цифры арабские в современном написании представляют собой абстрактные начертания, т.е. каждый графем не связан с величиной числа, который он отображает.

Перевод чисел из одной системы счисления в другую.

Программные средства для выполнения типовых расчетов.

Основные сведения об электронных таблицах.

Часто возникает необходимость создавать таблицы, в которых нужно выполнять математические операции с имеющимися данными. Для примера рассмотрим фрагмент таблицы учета товаров на складе (рис. 6.1). В данной таблице жирным шрифтом выделены числа, для получения которых нужно выполнить математические расчеты. Можно вычислить суммы на калькуляторе и вручную ввести готовые значения, но, изучив основы работы в программе Excel, вы сможете получить результаты автоматически, что сэкономит время и избавит от возможных ошибок.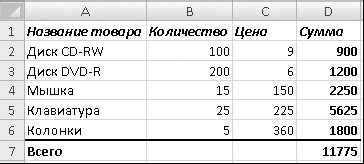

Рис. 6.1. Пример таблицы с вычислениями

Любая электронная таблица состоит из ячеек, которые образуют строки и столбцы.

Строки – это горизонтальные ряды ячеек, которые нумеруются цифрами (1, 2, 3). Столбцыпредставляют собой вертикальные ряды ячеек и обозначаются одной или двумя латинскими буквами (A, B, C).

Одна электронная таблица называется рабочим листом или просто листом. Максимальное количество столбцов в листе Excel 2007 составляет 16 384, а строк – более 1 млн, что значительно больше, чем в предыдущих версиях программы. Файлы электронных таблиц обычно состоят из нескольких листов и называются книгами.

Место каждой ячейки в таблице определяется ссылкой. Она образуется из обозначений столбца и строки, на пересечении которых находится ячейка. Например, цена диска CD-RW введена в ячейку C2, а итоговая сумма – в ячейку D7 (см. рис. 6.1). Вместо термина ссылка на ячейкумогут также употребляться термины имя ячейки или адрес ячейки.

В ячейки электронной таблицы можно вводить текст, числа и даты, а также формулы. Формула – это математическое выражение, по которому производятся вычисления в таблице. Например, в ячейку D2 (см. рис. 6.1) была введена следующая формула: =B2*C2. По этой формуле Excel автоматически перемножит содержимое ячеек B2 и C2 и отобразит результат в ячейке D2. Аналогичные формулы необходимо ввести в остальные ячейки столбца D. Формула всегда начинается со знака =, после которого вводятся ссылки на ячейки и знаки математических операций. В Excel существуют средства для автоматизации ввода формул, которые будут подробно рассмотрены в следующих уроках.

ПРИМЕЧАНИЕ

С документами в форме таблиц вы уже сталкивались при изучении программы Word, где имеются мощные средства для редактирования и форматирования, однако возможности для автоматических вычислений ограничены. Если в вашей таблице отсутствуют вычисления, то предпочтительнее использовать Word.

Встроенные функции.

Основные функции и их назначение

Функция

Результат

Назначение

Дата и время (всего 14)

=СЕГОДНЯ()

07.12.13

Читает текущую дату из системных часов ПК

=ДАТА(2006;5;12)

12.05.06

Возвращает дату в числовом формате

=ВРЕМЯ(18;32;15)

6:32 РМ

Возвращает время в числовом формате

Математические (всего 50)

=ABS(-5)

5

Модуль числа

=SIN(9O)

0,893997

Синус числа (в радианах)

=РАДИАНЫ(170)

2,96706

Преобразует радианы в градусы

=ГРАДУСЫ(30)

1718,873

Преобразует градусы в радианы

=ЕХР(5)

148,4132

Экспонента (е =2,71828182845904)

=LN(7)

1,94591

Натуральный логарифм

=LOG(7;5)

1,209062

Логарифм числа по заданному основанию

=КОРЕНЬ(256)

16

Квадратный корень

=ФАКТР(7)

5040

Факториал

=ОКРУГЛ(45,827;2)

45,83

Округляет до заданного числа десятичных разрядов

=ПИ()

3,141592 65358979

Число пи, округленное до 15 разрядов

=РИМСКОЕ(454)

CDLY

Преобразует число

в римский текстовый формат

=МОПРЕД(А1:СЗ)

–273

Определитель матрицы (здесь матрица = -[1;1;10;2;5;2;7;3;3])

Статистические (80 функций)

Для статистического

анализа диапазонов данных

Финансовые (53 функции)

Для типичных финансовых расчетов

Инженерные

Устанавливаются дополнительно через пункт меню «Сервис-> Надстройки ->Пакет анализа»

Ссылки и массивы (всего 17)

Обработка индексов и массивов

Работа с базой данных (всего 12)

Извлечение и обработка записей в базах данных

Текстовые (всего 23)

=ДЛСТР("Бабочка")

7

Длина текста

=ЗАМЕНИТЬ("Лампочка";3;2; "ст")

Ласточка

Замена символов внутри текста

=ПРАВСИМВ("Лампочка";5)

Почка

Правые символы слова

=НАЙТИ("ана";"Банан и ананас")

2

Ищет текст и возвращает найденную позицию

=ПОДСТАВИТЬ("ананас";"ан";"с")

Ссас

Заменяет один текст другим

=СЦЕПИТЬ("Само";"лет")

Самолет

Сцепляет слова

Логические (всего 6)

=ИЛИ(ИСТИНА;ЛОЖЬ; ЛОЖЬ)

ИСТИНА

Логическое ИЛИ

=И(ИСТИНА;ЛОЖЬ)

ЛОЖЬ

Логическое И

=НЕ(ИСТИНА)

ЛОЖЬ

Логическое НЕ

=EСЛИ(F1>5;10;5)

10 (здесь F1=7);
5 (здесь Fl=3)

Проверяет условие и возвращает одно из двух значений

=ЕНЕТЕКСТ(155)

ИСТИНА

Если не текст, возвращает логическое значение ИСТИНА

=ЕЧИСЛО("Текст")

ЛОЖЬ

Если число, возвращает логическое значение ИСТИНА

Условные и логические функции.

Понятие логических функций и их виды К логическим функциям относятся такие функции, которые позволяют выбрать то или иное решение в зависимости от того, выполняется или нет одно или несколько условий. С помощью этих функций в Excel можно предпринять одно действие, если условие выполняется, и другое - если условие не выполняется. Под условием в Excel понимается запись: Выражение № 1, условный оператор, выражение № 2 К условным операторам относятся: Оператор Значение Пример < меньше, чем B1<="меньше" или="" равно="" b1<="С4" > больше, чем В1>С4 >= больше или равно B1>=C4 = равно B1=C4 <> не равно B1<>C4 Выражением могут быть адрес или имя ячейки, функция, число, текст и их комбинация. Например: А2="Прибыль" СУММ(А1:А5)>20/2

К основным логическим функциям относят: ЕСЛИ (бывает простая и сложная); И; ИЛИ ; HE.
Подбор аргумента, при котором функция имеет заданное значение.

1.1. Подбор параметра

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность (относительная погрешность) устанавливаются следующей последовательностью команд:

щёлкнуть мышкой по кнопке меню <Сервис>;
в раскрывшемся меню щёлкнуть мышкой по строке <Параметры>;
в появившемся диалоговом окне <Параметры> щёлкнуть мышкой по вкладке <Вычисления>;
во вкладке уменьшить относительную погрешность до 0,000001 (окно <Относительная погрешность:>);
в окне <Предельное количество итераций>, при желании, можно увеличить количество итераций. Однако это едва ли улучшит искомый результат;

При подборе параметра Excel изменяет значение аргумента функции в одной конкретной ячейке до тех пор, пока вычисления функции по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

Реализация решения этим средством сводится к следующим действиям:

в выбранную ячейку рабочего листа ввести текст , например, в ячейку B5 ;
в соседнюю ячейку справа ввести значение начальной границы заданного отрезка функции, например, в ячейку C5;
- в соседнюю ячейку (строкой ниже) ввести текст , например, в ячейку B6;
- в соседнюю ячейку (справа от предыдущей) ввести формулу, в качестве которой использовать левую часть приравненного к нулю уравнения, например, в ячейку C6 ввести =C5*TAN(C5)-1. Эта формула соответствует уравнению вида:
tgx = 1/x или xtg(x) - 1 = 0;
щёлкнуть мышкой по кнопке меню <Сервис>;
в раскрывшемся меню щёлкнуть мышкой по строке <Подбор параметра>;
в появившемся диалоговом окне <Подбор параметра> удалить адрес текущей ячейки в окне <Установить в ячейке:> и щёлкнуть мышкой по ячейке с формулой, в окно <Значение:> ввести 0 (ноль), щелкнуть мышкой в окне <Изменяя значение ячейки:>, а затем щёлкнуть мышкой по ячейке со значением X;
щёлкнуть мышкой по кнопке <ОК>. Результат получен.

Решение нелинейного уравнения.

Отделение корней уравнения.

В общем случае отделение корней уравнения f(x)=0 базируется на известной теореме, утверждающей, что если непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)ґf(b)Ј0, то в указан-ном промежутке содержится хотя бы один корень. Например, для уравнения f(x)= x³-6x+2=0 видим, что при x®Ґ f(x)>0, при x®-Ґ f(x)<0, что уже свидетельствует о наличии хотя бы одного корня.

В общем случае выбирают некоторый диапазон, где могут обнаружиться корни, и осуществляют "прогулку" по этому диапазону с выбранным шагом h для обнаружения перемены знаков f(x), т.е. f(x)ґf(x+h)<0.

При последующем уточнении корня на обнаруженном интервале не надейтесь никогда найти точное значение и добиться обращения функции в нуль при использовании калькулятора или компьютера, где сами числа представлены ограниченным числом знаков. Здесь критерием может служить приемлемая абсолютная или относительная погрешность корня. Если корень близок к нулю, то лишь относительная погрешность даст необходимое число значащих цифр. Если же он весьма велик по абсолютной величине, то критерий абсолютной погрешности часто дает совершенно излишние верные цифры. Для функций, быстро изменяющихся в окрестности корня, может быть привлечен и критерий: абсолютная величина значения функции не превышает заданной допустимой погрешности.

Метод дихотомии.

Самым простейшим из методов уточнения корней является метод половинного деления, или метод дихотомии, предназначенный для нахождения корней уравнений, представленных в видеf(x)=0.

Пусть непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е.f(a)f(b)0 (рис. 1), тогда на отрезке имеется хотя бы один корень.

Возьмем середину отрезка с=(a+b)/2. Если f(a)f(c)0, то корень явно принадлежит отрезку от aдо (a+b)/2 и в противном случае от (a+b)/2 до b.

Поэтому берем подходящий из этих отрезков, вычисляем значение функции в его середине и т.д. до тех пор, пока длина очередного отрезка не окажется меньше заданной предельной абсолютной погрешности (b-a)<.

Так как каждое очередное вычисление середины отрезка c и значения функции f(c) сужает интервал поиска вдвое, то при исходном отрезке [a,b] и предельной погрешности  количество вычислений n определяется условием (b-a)/2ⁿ<, или nlog₂((b-a)/). Например, при исходном единичном интервале и точности порядка 6 знаков ( 10^-6) после десятичной точки достаточно провести 20вычислений (итераций) значений функции.

С точки зрения машинной реализации (рис. 2) этот метод наиболее прост и используется во многих стандартных программных средствах, хотя существуют и другие более эффективные по затратам времени методы.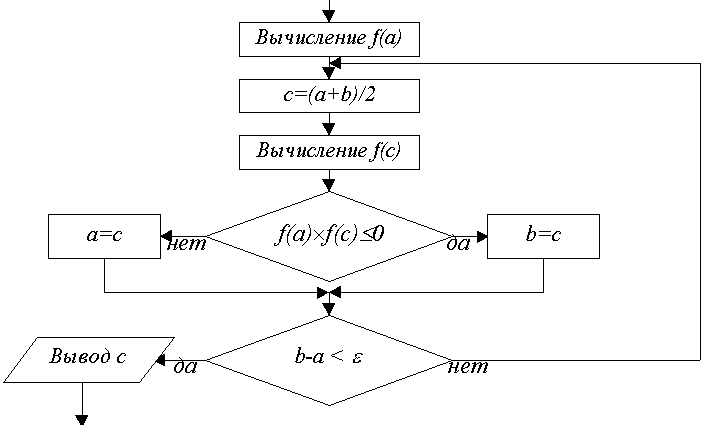

$c:\users\ирина\desktop\gl1-003.gif$

Решение систем линейных уравнений.

Методы Якоби и Гаусса-Зайделя.

Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. А чтобы решить реальную СЛАУ, лучше применить в Excel метод обратной матрицы или воспользоваться специальными программами, например, этой

Метод Гаусса

Краткое описание.

Решаю систему уравнений: A*X=B, где A - квадратная матрица n-го порядка, X,B - вектора
К матрице A справа приписываю вектор B. Получаю расширенную матрицу A
В дальнейшем A обозначает расширенную матрицу (n строк, n+1 столбец)
Aij - обозначает элемент матрицы, находящийся на i-й строке и j-м столбце
Делю 1-ю строку на A11, т е A'1j = A1j/A11 (j = 1..n+1). В результате A'11 = 1. A' обозначает преобразованную строку
Преобразую остальные строки по формуле: A'ij = Aij - A'1j*Ai1 (i = 2..n; j = 1..n+1)
В результате 1-й столбец в строках 2..n заполнится нулями
Отметим, что все эти преобразования не нарушают правильность уравнений
Аналогичные действия проводим для обнуления 2-го столбца в строках 3..n, то есть:
Делю 2-ю строку на A'22, т е A''2j = A'2j/A'22 (j = 2..n+1). В результате A''22 = 1. A'' обозначает резельтат 2-го преобразования строки
Преобразую остальные строки по формуле: A''ij = A'ij - A''2j*A'i2 (i = 3..n; j = 2..n+1)
В результате 2-й столбец в строках 3..n заполнится нулями
Аналогичные действия проводим далее
В результате левые n столбцов матрицы A превращаютс в верхнюю треугольную матрицу, т е ниже главной диагонали находятся только нули (а на главной диагонали - единицы) - см Рис 1. На этом рисунке вектор B - слева, S - номер шага

Затем выполняется "обратный ход", начиная с нижней строки, из которой можно вычислить Xn = Bn/Ann, например: Х4 = 9,55741/68,6388 = 0,13924 (рис. 1)
Затем можно вычислить X3 = (0,9065 - 2,40919*0,13924) = 0,57059
Затем из второй строки: X2 + 2,83562*X3 + 8,17808*X4 = 2,47945 вычисляю X2, и т д

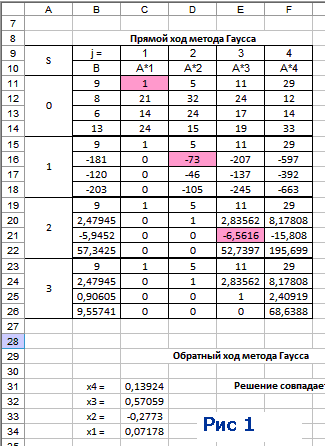
3. Метод Якоби (метод простых итераций)

Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.

Далее номер в скобках означает номер строки. Новую первую строку получаю сложением старой первой строки с другими строками, умноженными на специально подобранные коэффициенты. Записываю это в виде формулы:

(1)’ = (1) + 0,43*(2) - 0,18*(3) – 0,96*(4)

(2)’ = (2) + 0,28*(1) – 1,73*(3) + 0,12*(4)

(3)’ = (3) – 0,27*(1) - 0,75*(2) + 0,08*(4)

(4)’ = (4) + 0,04*(1) – 6,50*(2) + 8,04*(3)
Примечание: подбор коэффицентов выполнен на листе "Анализ".

Решаются системы уравнений, цель которых - обратить внедиагональные

элементы в нуль. Коэффиценты - это округлённые результаты решения

таких систем уравнений. Конечно, это не дело.
В результате получаю систему уравнений: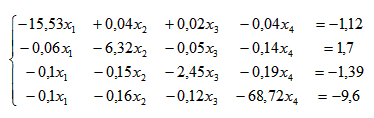

Для применения метода Якоби систему уравнений нужно преобразовать к виду:
X = B2 + A2*X Преобразую: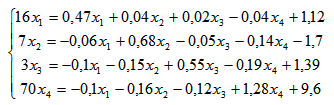

Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид :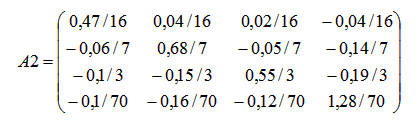

А вектор В2: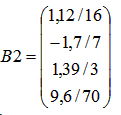

Методы оптимизации.

Поиск минимума функции одной переменной методом «тяжелого шарика».

Метод базируется на аналогии с движением тяжелого материального шарика по наклонной поверхности. Скорость шарика при движении вниз будет возрастать, и он будет стремиться занять нижнее положение, т.е. точку минимума.

X_i+1= X_i - (X_i –X_i-1) – h gradF(X_i)

При  = 0 – метод превращается в обычный градиентный. При 0 <  < 1 можно получать различную эффективность метода, которая будет зависеть и от h. Вдали от оптимума поиск будет ускоряться, а вблизи возможны колебания около минимума.

 - определяет память алгоритма, т.е учитывает влияние предыдущей точки, поэтому увеличение этого параметра вблизи минимума может привести к более быстрому затуханию, если градиент функции мал. Предпочтителен, когда глобальный минимум ярко выражен и локальные мелки.
Методы многомерной и условной оптимизации.

Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Методы линейного программирования.

Постановка распределительной задачи.

Пусть некоторое предприятие может изготавливать изделия четырех видов И₁ и И₂, И₃, И₄. Известно, что для изготовления изделия требуются три вида оборудования: О₁, О₂, О₃. Известно также, сколько времени потребуется на изготовление каждого изделия на каждом оборудовании, фонд времени работы оборудования (сколько времени может проработать каждое оборудование) и какая прибыль может быть получена при реализации каждого изделия (табл. 2.11).

Таблица 2.11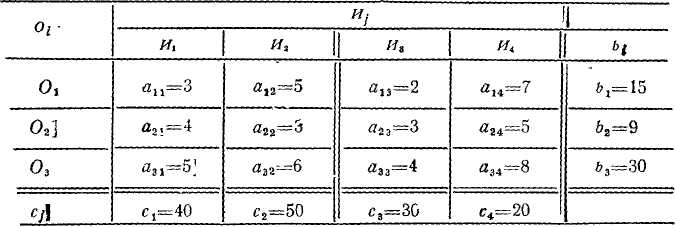

http://inf.docdat.com/tw_files2/urls_1/515/d-514829/514829_html_m77f32129.jpg

Необходимо так распределить изделия по оборудованиям, чтобы предприятие имело максимальную прибыль. Исходные данные расчета сведены в табл. 2.11. Обозначим: b_i — ресурсы оборудования O_r, а_ij — время изготовления i-го изделия И_i на j-м оборудовании; с_j — прибыль от одного изделия И_j; х_j — количество изделий, которое необходимо выпустить на предприятии.

Понятия целевой функции и ограничений.

Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:

(2)

(3)

(4)

(5)

При этом система линейных уравнений (3) и неравенств (4), (5), определяющая допустимое множество решений задачи ^ W, называется системой ограничений задачи линейного программирования, а линейная функция f(Х) называется целевой функцией или критерием оптимальности.

В самом общем виде задача линейного программирования математически записывается следующим образом:

(1)

где X = (x₁, x₂ , ... , x_n); W – область допустимых значений переменных x₁, x₂ , ... , x_n ;f(Х) – целевая функция.

Решение распределительной задачи.

Аппроксимация функций.

Подбор эмпирических зависимостей.

Эмпирическая формула — формула, показывающая тип и соотношение элементов в соединении.

1

Проще всего построить график функции тренда непосредственно сразу после внесения имеющихся данных в массив. Для этого на листе с таблицей данных выделите не менее двух ячеек диапазона, для которого будет построен график, и сразу после этого вставьте диаграмму. Вы можете воспользоваться такими видами диаграмм, как график, точечная, гистограмма, пузырьковая, биржевая. Остальные виды диаграмм не поддерживают функцию построения тренда.

2

В меню «Диаграмма» выберите пункт «Добавить линию тренда». В открывшемся окне на вкладке «Тип» выберите необходимый тип линии тренда, что в математическом эквиваленте также означает и способ аппроксимации данных. При использовании описываемого метода вам придется делать это «на глаз», т.к. никаких математических вычислений для построения графика вы не проводили.

3

Поэтому просто прикиньте, какому типу функции более всего соответствует график имеющихся данных: линейной, логарифмической, экспоненциальной, степенной или иной. Если же вы сомневаетесь в выборе типа аппроксимации, можете построить несколько линий, а для большей точности прогноза на вкладке «Параметры» этого же окна отметить флажком пункт «поместить на диаграмму величину достоверности аппроксимации (R^2)».

4

Сравнивая значения R^2 для разных линий, вы сможете выбрать тот тип графика, который характеризует ваши данные наиболее точно, а, следовательно, строит наиболее достоверный прогноз. Чем ближе значение R^2 к единице, тем точнее вы выбрали тип линии. Здесь же, на вкладке «Параметры», вам необходимо указать период, на который делается прогноз.

5

Такой способ построения тренда является весьма приблизительным, поэтому лучше все-таки произвести хотя бы самую примитивную статистическую обработку имеющихся данных. Это позволит построить прогноз более точно.

6

Если вы предполагаете, что имеющиеся данные описываются линейным уравнением, просто выделите их курсором и произведите автозаполнение на необходимое число периодов, или количество ячеек. В данном случае нет необходимости находить значение R^2, т.к. вы заранее подогнали прогноз к уравнению прямой.

7

Если же вы считаете, что известные значения переменной лучше всего могут быть описаны с помощью экспоненциального уравнения, также выделите исходный диапазон и произведите автозаполнение необходимого количества ячеек, удерживая правую клавишу мыши. При помощи автозаполнения вы не сможете построить других типов линий, кроме двух указанных.

8

Поэтому для наибольшей точности построения прогноза вам придется воспользоваться одной из нескольких статистических функций: «ПРЕДСКАЗ», «ТЕНДЕНЦИЯ», «РОСТ», «ЛИНЕЙН» или «ЛГРФПРИБЛ». В этом случае вам придется высчитывать значение для каждого последующего периода прогноза вручную. Если вам необходимо произвести более сложный регрессионный анализ данных, вам понадобится надстройка «Пакет анализа», которая не входит в стандартную установку MS Office.

Метод наименьших квадратов.

Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных.

Для того, чтобы установивить линейную зависимость для заданных табличных данных с помощью Excel, необходимо выполнить следующие действия:

В ячейки A1 и B1 ввести текст соответственно «xi» и «yi».
Заполнить диапазон ячеек A2:B6 значениями из таблицы:

x₀

y₀

x₁

y₁

.

.

.

.

.

.

x_n

y_n
В ячейку С1 ввести текст n=.
В ячейку D1 ввести число 4.
В ячейки C2:С5 ввести текст «Mx», «My», «Mxy», «Mx2» соответственно.
В ячейку D2 ввести формулу =СУММ(A2:A6).
В ячейку D3 ввести формулу =СУММ(B2:B6).
В ячейки A8, B8 ввести текст «x*y», «x^2» соответственно.
В ячейку A9 ввести формулу =A2*B2 и методом протягивания заполнить диапазон ячеек A10:A13.
В ячейку B9 ввести формулу =A2^2 и методом протягивания заполнить диапазон ячеек B10:B13.
В ячейку D4 ввести формулу =СУММ(A9:A13).
В ячейку D5 ввести формулу =СУММ(B9:B13).
В ячейки D8, D11, D14 текст «D=», «D1=», «D2=» соответственно.
В ячейку E8 и F9 ввести формулу = D2.
В ячейку E9 ввести формулу =D5.
В ячейку F8 ввести формулу =D1+1.
В ячейку H8 ввести текст «D=».
В ячейку I8 ввести формулу =МОПРЕД(E8:F9) (вычисляет определитель матрицы).
В ячейку E11 ввести формулу =D3.
В ячейку E12 ввести формулу =D4.
В ячейку F11 ввести формулу =D1+1.
В ячейку F12 ввести формулу =D2.
В ячейку H11 ввести текст «D1=».
В ячейку I11 ввести формулу =МОПРЕД(E11:F12) (вычисляет определитель матрицы).
В ячейку E14 ввести формулу =D2.
В ячейку E15 ввести формулу =D5.
В ячейку F14 ввести формулу =D3.
В ячейку F15 ввести формулу =D4.
В ячейку H14 ввести текст «D2=».
В ячейку I14 ввести формулу =МОПРЕД(E14:F15) (вычисляет определитель матрицы).
В ячейки A16 и A17 ввести текст «a=», «b=» соответственно.
В ячейку B16 ввести формулу =I11/I8.
В ячейку B17 ввести формулу =I14/I8.

В итоге получаем следующее: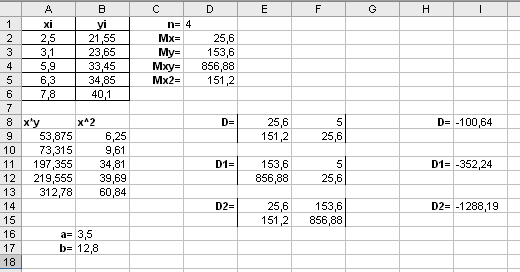

изобажение итогового результата

Ответ: g=3,5x+12,8.

Решение обыкновенных дифференциальных уравнений 1го порядка.

Метод Эйлера.

Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление»^[1]. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно-линейной функцией, т. н. ломаной Эйлера.

Описание.

Пусть дана задача Коши для уравнения первого порядка

$\frac{dy}{dx}=f(x,y),$

$y_{|_{x=x_0}}=y_0,$

где функция

определена на некоторой области $d\subset r^2$ . Решение ищется на интервале

. На этом интервале введем узлы

$x_0<x_1<\dots<x_n\le b.$

Приближенное решение в узлах

, которое обозначим через

определяется по формуле

$y_i=y_{i-1}+(x_i-x_{i-1})f(x_{i-1},y_{i-1}),\quad i=1,2,3,\dots,n.$

Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

Оценка погрешности.

Метод Эйлера является методом первого порядка. Если функция

непрерывна в

и непрерывно дифференцируема по переменной

, то имеет место следующая оценка погрешности

$\left|y(x_i)-y_i\right|=o(h),$

где

— средний шаг, то есть существует

такая, что $c^{-1}\le (x_i-x_{i-1})/h\le c$ .

Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.

Значение.

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Модификация метода Эйлера.

Вычисления по методу Эйлера с пересчетом делаются в два этапа.

Прогноз:

$\tilde y_i=y_{i-1}+(x_i-x_{i-1})f(x_{i-1},y_{i-1})$ .

Коррекция:

$y_i=y_{i-1}+(x_i-x_{i-1})\frac{f(x_{i-1},y_{i-1})+f(x_i,\tilde y_i)}{2}$ .

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции.