Статистика №1. Пракимческая работа 1

• Название: Пракимческая работа 1
• Дата: 01.02.2023
• Размер: 250.22 Kb.
• Имя файла: Статистика №1.docx
• Тип: Документы; #916156
• страница: 1 из 3

Пракимческая работа № 1

Построение вариационных рядов. Расчет числовых характеристик
1. Цель работы

• 
  Овладение способами построения рядов распределения и методами расчета числовых характеристик.
  

2. Перечень справочной литературы

3. Краткие теоретические сведения
Выполнение самостоятельной работы № 3 рассмотрим на примере следующей задачи.

З а д а ч а. Имеются данные о совершении преступлений небольшой тяжести в городе N (в ):

61,2	61,4	60,2	61,2	61,3	60,4	61,4	60,8	61,2	60,6
61,6	60,2	61,3	60,3	60,7	60,9	61,2	60,5	61,0	61,4
61,1	60,9	61,5	61,4	60,6	61,2	60,1	61,3	61,1	61,3
60,3	61,3	60,6	61,7	60,6	61,2	60,8	61,3	61,0	61,2
60,5	61,4	60,7	61,3	60,9	61,2	61,1	61,3	60,9	61,4
60,7	61,2	60,3	61,1	61,0	61,5	61,3	61,9	61,4	61,3
61,6	61,0	61,7	61,1	60,9	61,5	61,6	61,4	61,5	61,2
61,6	61,3	61,8	61,1	61,7	60,9	62,2	61,1	62,1	61,0
61,5	61,7	62,3	62,3	61,7	62,9	62,5	62,8	62,6	61,5
62,1	62,6	61,6	62,5	62,4	62,3	62,1	62,3	62,2	62,1

Задание: на основе совокупности данных опыта выполнить следующее:

1. 
   Построить ряды распределения (интервальный и дискретный вариационные ряды). Изобразить их графики.
   
2. 
   Построить график накопительных частот — кумуляту.
   
3. 
   Составить эмпирическую функцию распределения и изобразить ее графически.
   
4. 
   Вычислить моду, медиану, выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс. Построить доверительные интервалы для истинного значения измеряемой величины и среднего квадратического отклонения генеральной совокупности.
   

РЕШЕНИЕ

Построить интервальный вариационный ряд. Для этого найти:

а) размах варьирования признака по формуле R = x_max - x_min,

где x_min – наименьшая, x_max – наибольшая варианты в данной выборочной совокупности;

б) число интервалов вариационного ряда, пользуясь одним из приведенных ниже соотношений



где n— объем выборки

в) длину hчастичных интервалов по формуле



и, если необходимо, округлить это значение до некоторого числа;

г) записать полученный интервальный вариационный ряд, заполнив таблицу 1

Таблица 1

Варианты-интервалы, ( xi 1 ; xi )	( x0 ; x1 )	( x1 ; x2 )	. . .	( xk 1 ; xk )
частоты, ni	n1	n2	. . .	nk

Сделать контроль, убедившись, что _ n_i n.

- Построить дискретный вариационный ряд, взяв в качестве варианта - середины вариант-интервалов непрерывного вариационного ряда, а в качестве частот — частоты непрерывного вариационного ряда (табл. 1).

- Изобразить графически интервальный и дискретный вариационные ряды (построить гистограмму и полигон частот).

Построить график накопленных частот — кумуляту, т.е. ломаную, проходящую через точки с координатами x_i и соответствующими накопленными частотами.

Найти эмпирическую функцию распределения и изобразить ее графически.

Найти моду M _oи медиану M _e .

Для вычисления остальных статистик воспользоваться методом произведений. Ввести условные варианты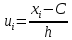



где C  M_o, h-шаг (длина интервала).

Контроль вычислений произвести по формуле:


i

i
_ n_i  2_n_iu_i  _n u ²  _ n_i (u_i  1)² .

Вычислить начальные моменты:




1
Найти выборочную среднюю.



Найти выборочную дисперсию




Найти выборочное среднее квадратическое отклонение:



Найти коэффициент вариации:V  S / .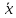
Выполнение работы

Обозначим через Х количество преступлений небольшой тяжести в городе N (в ).

1. 
   По данным выборки строим интервальный вариационный ряд.
   

а) Поскольку, как легко выяснить, x_max = 62,8, x_min = 60,1, то размах варьирования признака Х равен R= x_max –x_min = 62,8 – 60,1 = 2,7.

б) Определяя число kинтервалов (число столбцов в таблице) вариа-

ционного ряда, положим k 10 .

в) Длина hкаждого частичного интервала равна



Так как исходные данные мало отличаются друг от друга и содержат один десятичный знак, то величину hокругляем до одного десятичного знака:

h  0,3 .

г) Подсчитываем число вариант, попадающих в каждый интервал, поданным выборки. Значение x_i, попадающее на границу интервала, относим к правому интервалу. За начало x₀ первого интервала берем величину ^x0 ^{ x}min 0,5h 60,1  0,5  0,3  59,95  60 . Конец x_kпоследнего интервала находим по формуле

^xk^{ x}max 0,5h 62,8  0,15  62,95  63,0 .

Сформированный интервальный вариационный ряд записываем в виде табл. 2.


Таблица 2

Варианты- интервалы	60- 60,3	60,3- 60,6	60,6- 60,9	60,9- 61,2	61,2- 61,5	61,5- 61,8	61,8- 62,1	62,1- 62,4	62,4- 62,7	62,7- 63,0
Частоты, ni	3	6	9	18	29	16	2	10	5	2

Контроль: _ n_i 100 , и объем выборки n  100 .

Записываем дискретный вариационный ряд (табл. 3). В качестве варианта x_i

берем середины интервалов интервального вариационного ряда

Таблица 3

варианты, xi	60,15	60,45	60,75	61,05	61,35	61,65	61,95	62,25	62,55	62,85
частоты, ni	3	6	9	18	29	16	2	10	5	2

Изображаем интервальный и дискретный вариационные ряды графически, построив гистограмму и полигон частот в одной системе координат (рис. 1).

Строим график накопленных частот — кумуляту (рис. 2). Предварительно составляем расчетную табл. 4.

Таблица 4

Варианты, xi	60,15	60,45	60,75	61,05	61,35	61,65	61,95	62,25	62,55	62,85
относительные частоты, wi= ni/ n	0,03	0,06	0,09	0,18	0,29	0,16	0,02	0,1	0,05	0,02
накопительные относительные частоты, Wi= Wi – 1 + wi	0,03	0,09	0,18	0,36	0,65	0,81	0,83	0,93	0,98	1

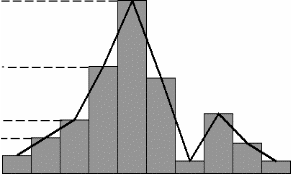0,29

0,18
0,09

0,06

0,03
0

60 60,3 60,6 60,9 61,2 61,5 61,8 62,1 62,4 62,7 63

Рис.1. Гистограмма и полигон.

Находим эмпирическую функцию распределения. Воспользуемся формулой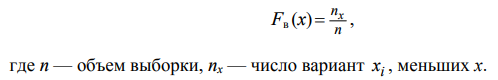



Записываем полученную эмпирическую функцию в виде: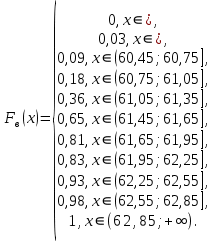



График функции F_в (x) представлен на рис.4.

Соединив середины вертикальных частей ступенчатой кусочно- постоянной кривой, являющейся графиком функции F_в (x), получаем плавную кривую (на рис. 4 это штриховая линия). Абсциссами точек этой кривой служат значения количества совершенных преступлений небольшой тяжести, а ординатами — значения эмпирической функции распределения, характеризующей оценку вероятности события X  x_i, т.е. вероятности попадания возможных значений количества преступлений небольшой тяжести на промежуток (, x_i].

Для нахождения числовых характеристик признака Х — количества преступлений небольшой тяжести (несмещенных оценок для M( X)  a, D( X) , а также M_eX,M_oX, A_s, E_x) воспользуемся табл. 8.

Так как варианта x  61,35 в табл. 8 встречается с наибольшей частотой

n₅  29 , то M_o X 61,35 , т.е. это значение процент количества преступлений небольшой тяжести, встречающееся в данной выборке с наибольшей частотой.

Находим M _e X . Так как табл. 8 содержит четное число столбцов, то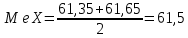

. Это значение процента количества преступлений небольшой тяжести, которое делит данные выборки признака Х на равные части.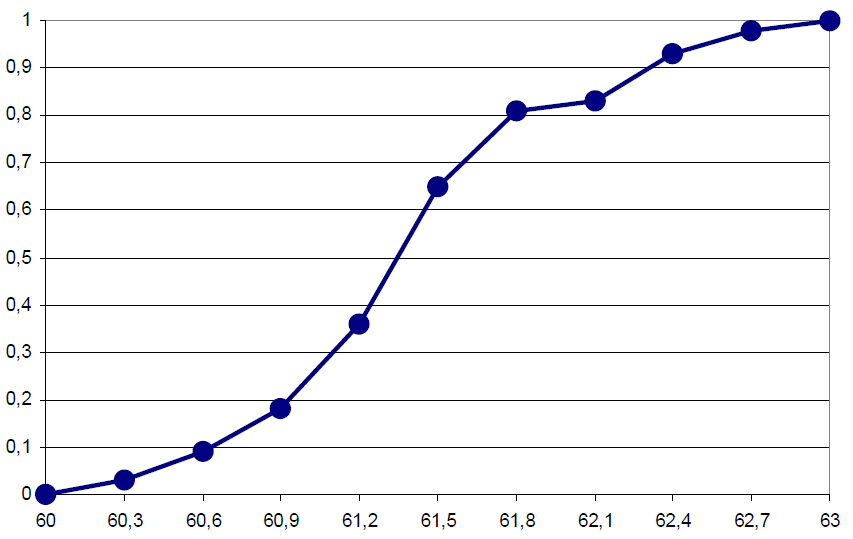


Рис. 2. Кумулятивная кривая.

Для нахождения остальных статистик, характеризующих процент количества преступлений небольшой тяжести, воспользуемся методом произведений. Введем условные варианты



Составим расчетную табл. 5.

Таблица 5

xi	ni	ui	niui	niu2i	niu3i	niu 4i	контрольный столбец ni (ui 1)2
60,15	3	– 4	– 12	48	– 192	768	27
60,45	6	– 3	– 18	54	– 162	486	24
60,75	9	– 2	– 18	36	– 72	144	9
61,05	18	– 1	– 18	18	– 18	18	0
61,35	29	0	0	0	0	0	29
61,65	16	1	16	16	16	16	64
61,95	2	2	4	8	16	32	18
62,25	10	3	30	90	270	810	160
62,55	5	4	20	80	320	1280	125
62,85	2	5	10	50	250	1250	72
	100		14	400	428	4804	528

Контроль вычислений проводим по формуле:

_ n_i  2_ n_iu_i  _n u ²  _n_i (u_i  1)² ,


i

i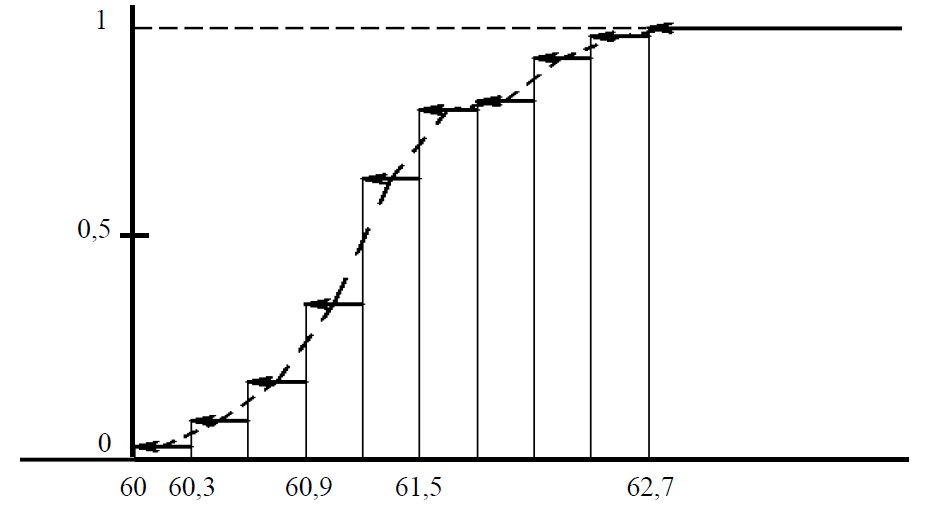



Рис.3. Кумулята и эмпирическая функция распределения.
т.е.100  2 14  400  528  27  24  9  29  64  18  160  125  72 .

Следовательно, вычисления проведены верно.

Пользуясь результатами последней строки табл. 10, находим условные начальные моменты: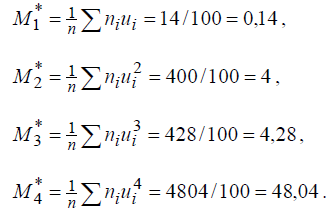



Находим выборочную среднюю:



которая характеризует средний процент количества преступлений небольшой тяжести в данной выборке, составляющую 61,39 %.

Находим выборочную дисперсию:

Вычисляем выборочное среднее квадратичное отклонение:



Величина S 0,599 характеризует степень рассеяния процент количества преступлений небольшой тяжести относительно средней процент количества преступлений небольшой тяжести. Для определения колеблемости значений процент количества преступлений небольшой тяжести в процентном отношении вычисляем коэффициент вариации: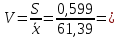

0,00976

Величина коэффициента вариации мала (составляет 0,01), что означает тесную сгруппированность значений процента количества преступлений небольшой тяжести около центра рассеяния, т.е. около среднего процента.