Практика математическое моделирование. Матмоделирование практика. Практическая работа 1 Методы формирования случайной величины с заданным законом распределения
 Скачать 244.2 Kb. Скачать 244.2 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ) Кафедра радиотехнических систем Практические работы по дисциплине «Математическое моделирование устройств и систем»
Москва 2023 Практическая работа №1 Методы формирования случайной величины с заданным законом распределения 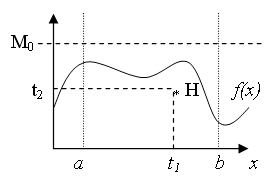  Рисунок 1 - Функция плотности вероятности Для формирования случайной величины с заданным законом распределения будем использовать Метод Неймана. Для моделирования случайной величины методом Неймана требуется ввести ограничения на область значений функции плотности вероятности f(x) генерируемого распределения (см. рисунок 1) Шаги реализации метода Неймана будут следующими: 1. Изобразить функцию плотности вероятности заданного процесса f(x) 2. Определить по графику ограничения на функцию f(x) по оси х (значения a и b) и по оси y (точку M0) 3. Зафиксировать численные значения параметров a, b, и Mo 4. С помощью ГСЧ сгенерировать две случайные величины γ1, γ2 и равномерно распределенные на интервале [0 1] 5. Вычислить значения, которые определяют координаты точки H(t1,t2): t1 = a+ γ1*(b-a); t2 = γ2*M0; 6. Если H(t1,t2) лежит под кривой f(x), то полагаем X=t1, записываем число в массив случайной величины, иначе – текущую пару (γ1, γ2) отбрасываем и выбираем новую пару значений (γ1, γ 2) . Повторяем шаги 5,6 с новой парой значений до тех пор, пока не наберется массив значений случайной величины достаточной длины. Рассмотрим распределение Эрланга Его функция плотности вероятности может быть записана в виде: 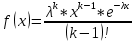 Примем следующие параметры распределения: 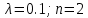 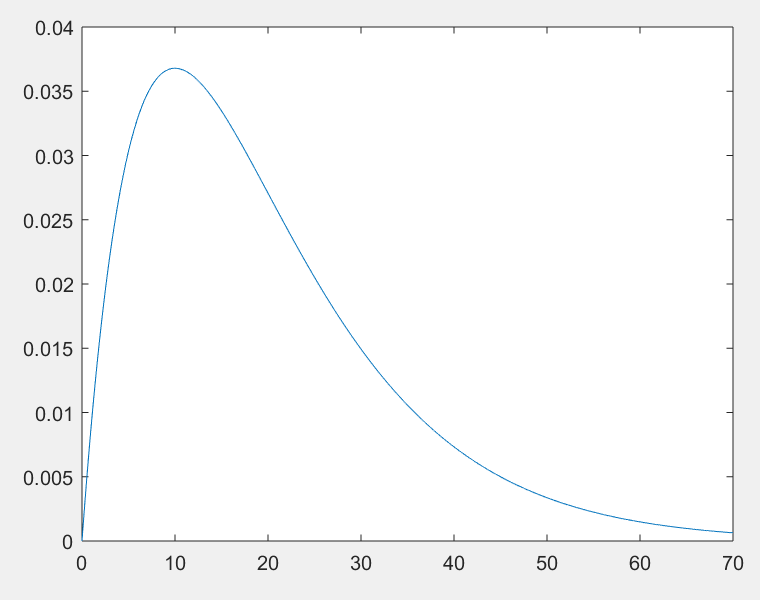  Рисунок 2 - Теоретическая функция плотности вероятности При следующих параметрах функция плотности вероятности примет следующий вид: Определим следующие границы функции плотности вероятности: a = 0, b = 60, M0 = 0.038 (определим из максимума функции плотности вероятности) Для выбранной длины выборки 50000 значений получаем следующий результат:  Рисунок 3 - Реализация метода Неймана на выборке из 50000 значений 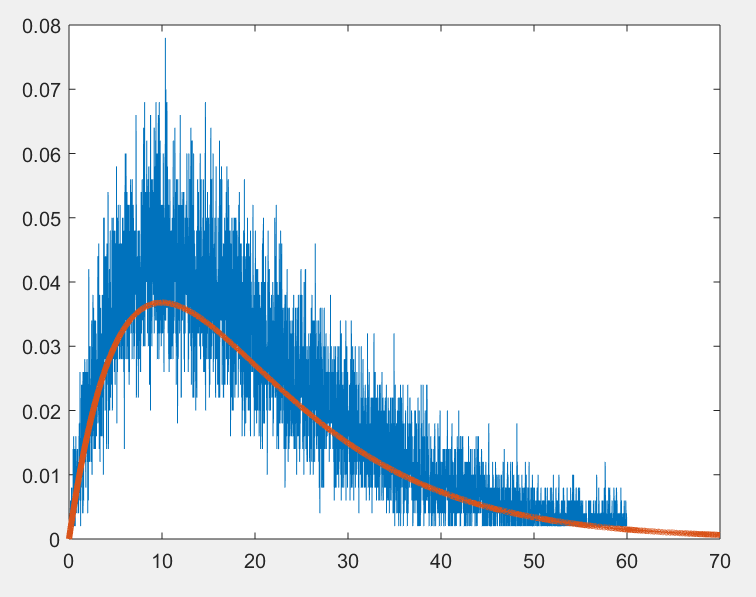 Синий график соответствует значениям, полученным при помощи метода Неймана 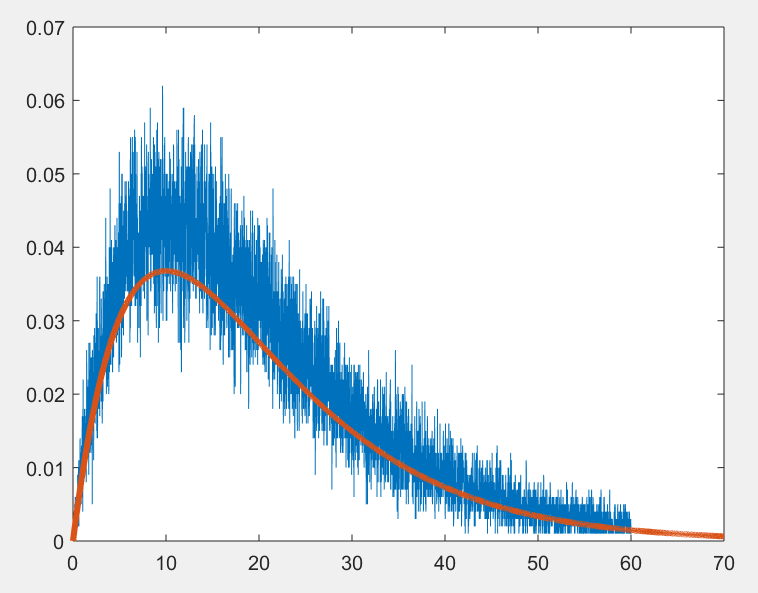  Рисунок 4 - Реализация метода Неймана на выборке из 100000 значений Для выборки 100000 получаем следующий результат: Как видно из рисунка резкие всплески значений, характерные для метода Неймана, сглаживаются. Отсюда можно сделать вывод, что для корректной работы метода требуется очень большая набранная статистика. Практическая работа №2 Метод наименьших квадратов для аппроксимации экспериментальных данных Выполнить аппроксимацию функции с помощью МНК (не используя встроенные функции для непосредственной аппроксимации). Функция задана следующей таблицей:
Степень полинома – 1 Рассчитаем коэффициенты по следующим формулам: 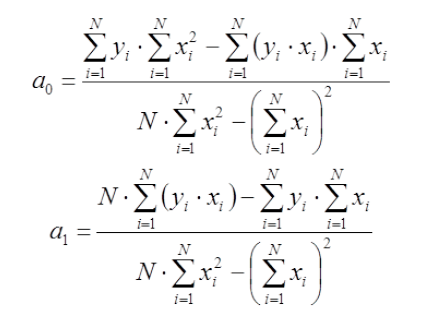 Запишем полученные коэффициенты полинома: 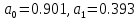 Таким образом, полученная функция имеет следующий вид: 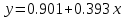 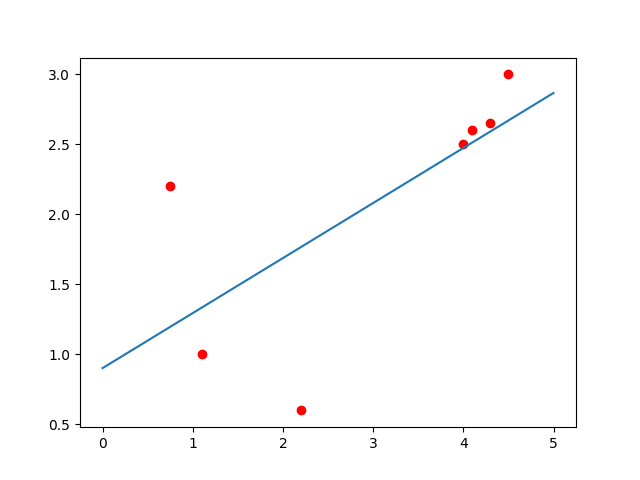  Рисунок 5 - Аппроксимирующая функция (синяя) и экспериментальные значения (красные) Зарисуем полученную аппроксимирующую функцию: Можно сделать вывод, что линейная функция не подходит для аппроксимации полученных данных, поскольку в левой части наблюдается очень сильный разброс между экспериментальными значениями. Практическая работа №3 Моделирование систем массового обслуживания методом Монте-Карло. Задание: В двухканальную систему массового обслуживания (СМО) с отказами поступает стационарный пуассоновский поток заявок. Время между поступлениями двух последовательных заявок распределено по показательному закону с параметром λ заявок в минуту. Длительность обслуживания каждой заявки равна Tобсл (мин). Методом Монте-Карло найти вероятность обслуживания. Оценить число требуемых испытаний. Время наблюдения 2.5 минуты. Условия: Tобсл = 0.5 мин λ = 5 ε = 0.01 Q = 95% 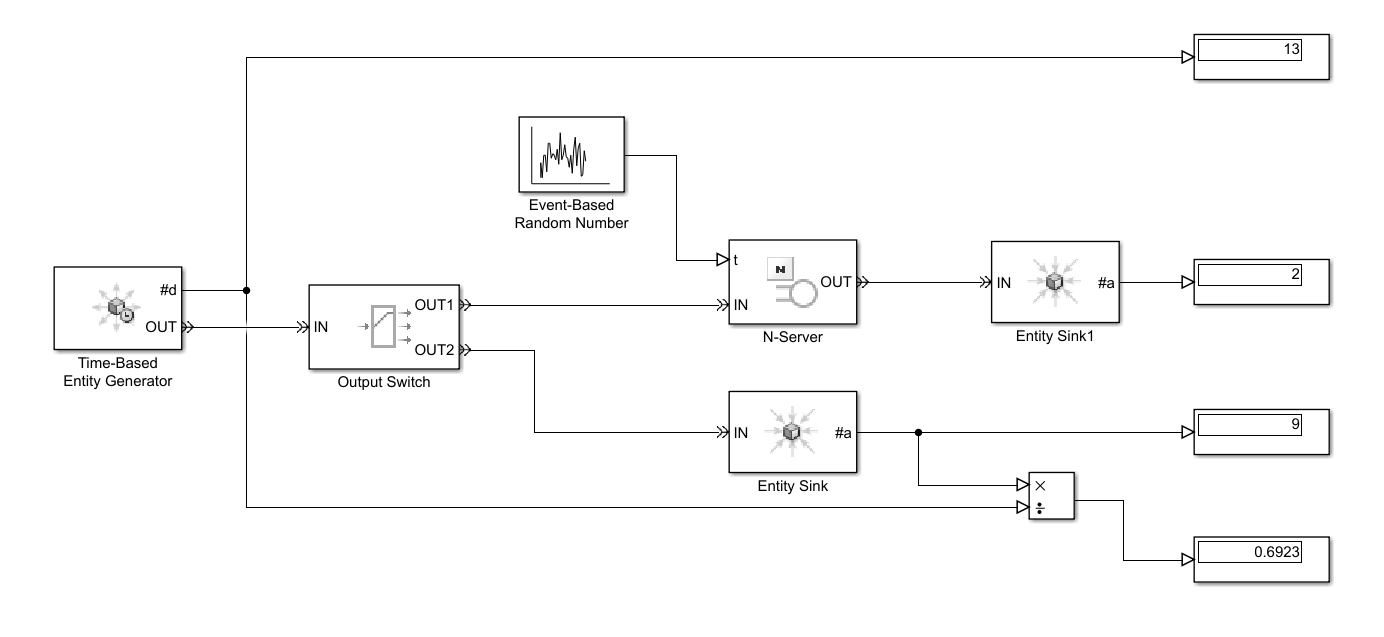  Рисунок 6 - Двухканальная система массового обслуживания с отказами Для моделирования процессов будем использовать пакет Simulink ПО Matlab. Соберем схему двухканальной системы массового обслуживания с отказами (рисунок 6) Выставим время – 2.5 минуты и запустим моделирование. По результатам видно, что из 13 клиентов успешно обслужились 2, отказались – 9, остались в системе – 2. Получена вероятность отказа – 0.6923, вероятность обслуживания – 0.3077. Найдем количество испытаний, необходимое для моделирования с параметрами точности ε и доверительной вероятности Q по формуле: 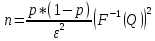 Тогда, n = 230 испытаний. При данном количестве испытаний вероятность отказа равна 0.4113, вероятность обслуживания – 0.5887. |
