Практические работы №1, №2. Практическая работа 1 Название практической работы Измерение информации

• Название: Практическая работа 1 Название практической работы Измерение информации
• Дата: 12.02.2021
• Размер: 35.4 Kb.
• Имя файла: Практические работы №1, №2.docx
• Тип: Практическая работа; #175975

Практическая работа №1

Название практической работы: Измерение информации

Цель работы: научиться измерять информацию различными методами, использовать правила перевода информации из одних единиц измерения в другие.
Теоретический материал:

Информативность сообщения зависит от многих причин.

Существует несколько подходов к вопросу информативности сообщения: субъективный (содержательный, объективный (алфавитный) и вероятностный.

Содержательный подход:

Научный подход к оценке сообщений был предложен еще в 1928 году Р. Хартли.

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий. Тогда количество информации, заключенное в этом сообщении, - I бит и число N связаны формулой:

2^I = N (1)

где I – количество информации или информативность события (в битах);

N – число равновероятных событий (число возможных выборов).

Следовательно, информативность события равна

I = log₂N (2)
Пример №1: При угадывании целого числа в диапазоне от 1 до N было получено 8 бит информации. Чему равно N?

Решение: Для того чтобы найти число, достаточно решить уравнение N=2^I, где I = 8. Поскольку 2⁸ = 256, то N = 256. Следовательно, при угадывании любого целого числа в диапазоне от 1 до 256 получаем 8 бит информации.
Объективный подход:

Информация рассматривается как последовательность символов, знаков.

Количество символов в сообщении называется длиной сообщения. Основой любого языка является алфавит.

Алфавит – это набор знаков (символов), в котором определен их порядок.

Есть алфавит, который можно назвать достаточным. Это алфавит мощностью 256 символов. Алфавит из 256 символов используется для представления текстов в компьютере. Поскольку 256=2⁸, то один символ этого алфавита «весит» 8 бит.8 бит информации присвоили свое название – байт.

Если один символ алфавита несет 1 байт информации, то надо просто сосчитать число символов, полученное значение даст информационный объем текста в байтах.

Для вычисления объема информации V используют формулу:

V = KI (3)

где I –информационный вес одного символа и находится по формуле (1), где N – мощность алфавита (количество символов);

K – количество символов в сообщении (тексте).

Пример №2: Племя “Обезьяны” пишет письма, пользуясь 32-символьным алфавитом. Племя “Слоны” пользуется 64-символьным алфавитом. Вожди племен обменялись письмами. Письмо племени “Обезьяны” содержало 90 символов, а письмо племени “Слоны” – 80 символов. Сравните объем информации, содержащейся в письмах.

Решение: Мощность алфавита племени “Обезьяны” равна 32, информационный вес одного символа алфавита I = log₂32 = 5 бит. Количество информации в тексте, состоящем из 90 символов, равно V= 90*5 = 450 бит = 56,25 байт.

В любой системе единиц измерения существуют основные единицы и производные от них. Для измерения больших объемов информации используются производные от байта единицы:

1 килобайт = 1 Кб = 2¹⁰ байт = 1024 байта; 1 мегабайт = 1 Мб = 2¹⁰ Кб = 1024 Кб

1 гигабайт = 1 Гб = 2¹⁰ Мб = 1024 Мб = 1048576 Кб = 1073741824 байт

1 Терабайт = 1024 Гбайт; 1 Петабайт = 1024 Терабайт; 1 экзабайт = 1024 Пбайт

1 зеттабайт = 1024 экзабайт; 1 йоттабайт = 1024 зеттабайт
Ход работы:

1. 
   Выполните перевод единиц измерения информации:
   

1. 
   5 Кбайт = __ байт = __ бит;
   
2. 
   __ Кбайт = __ байт = 12288 бит;
   
3. 
   __ Кбайт = __ байт = 213 бит;
   
4. 
   __Гбайт = 1536 Мбайт = __ Кбайт;
   
5. 
   512 Кбайт = __ байт = __ бит;
   
6. 
   4Гбайт 5Кбайт 8000 бит = ___Мбайт;
   
7. 
   2 Кбайт 8008 бит = ___ байт;
   
8. 
   2³³ бит = ___ Гбайт.
   

2. 
   Используя содержательный подход к измерению информации, решите задачи:
   

1. 
   Определите количество информации, полученное при отгадывании числа из интервала от 0 до 31;
   
2. 
   Сообщение о том, что Иванов живет на 12 этаже несет 4 бита информации. Определите количество этажей в доме.
   
3. 
   Шарик находится в одном из 64 ящичков. Посчитайте сообщения о том, где находится шарик;
   
4. 
   Определите количество бит информации в сообщении о том, что на светофоре горит зеленый свет;
   
5. 
   Определите количество информации, полученной вторым игроком при игре в крестики-нолики на поле 8х8, после первого хода первого игрока, играющего крестиками;
   
6. 
   Вы бросаете два кубика с нанесенными на гранях цифрами от 1 до 6. Определите, сколько бит информации несет сообщение, что на одном кубике выпала тройка, а на другом – пятерка.
   

3. 
   Используя алфавитный подход к измерению информации, решите задачи:
   

1. 
   Сообщение, записанное буквами 64-х символьного алфавита, содержит 20 символов. Определите, какой объем информации оно несет. Результат перевести в байты;
   
2. 
   Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Определите количество символов, содержащихся в алфавите, при помощи которого было записано это сообщение;
   
3. 
   Подсчитайте количество килобайт информации в тексте, если текст состоит из 600 символов, а мощность используемого алфавита – 128 символов;
   
4. 
   Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Определите объем информации, содержащейся в 5 страницах текста;
   
5. 
   Лазерный принтер печатает со скоростью в среднем 7 Кбит в секунду. Сколько времени понадобится для распечатки 12-ти страничного документа, если известно, что на одной странице в среднем по 45 строк, в строке 60 символов (1 символ – 1 байт). Результат округлите до целой части;
   
6. 
   Имеется 2 текста на разных языках. Первый текст использует 32-символьный алфавит и содержит 200 символов, второй – 16-символьный алфавит и содержит 250 символов. Определите, какой из текстов содержит большее количество информации и на сколько бит;
   
7. 
   Определите количество символов в сообщении, записанном с помощью 16-символьного алфавита, если объем этого сообщения составил 1/16 Мб;
   
8. 
   Для записи сообщения использовался 64-символьный алфавит. Каждая страница содержит 30 строк. Все сообщение содержит 8775 байтов информации и занимает 6 страниц. Определите количество символов в строке.
   

4. 
   Решите задачи на измерение информации:
   

1. 
   Считая, что каждый символ кодируется одним байтом, оцените информационный объем следующего предложения: «HTML – это язык гипертекстовой разметки документа»;
   
2. 
   Разведчик А. Белов должен передать сообщение: «Место встречи изменить нельзя. Юстас» Пеленгатор определяет место передачи, если она длится не менее 2 минут. С какой скоростью (бит/с) должен передавать радиограмму разведчик?
   
3. 
   Сколько различных комбинаций можно построить, используя четыре двоичных разряда?
   

5. 
   Полученные результаты занесите в итоговую таблицу.
   
6. 
   Ответьте на контрольные вопросы:
   

• 
  Перечислите подходы к измерению информации;
  
• 
  Запишите формулу вычисления объема информации.
  

7. 
   Оформите и сдайте отчет преподавателю.
   

Практическая работа №2

Название практической работы: Применение теоремы Шеннона

Цель работы: научиться измерять информацию, используя вероятностный подход, применять данный метод при решении задач.

Теоретический материал:

Рассмотренная в практической работе №1 формула Хартли является частным случаем, так как применяется только к равновероятным событиям. В жизни же мы сталкиваемся не только с равновероятными событиями, но и событиями, которые имеют разную вероятность реализации.

Например:

1. 
   Когда сообщают прогноз погоды, то сведения о том, что будет дождь, более вероятно летом, а сообщение о снеге - зимой.
   
2. 
   Если на озере живет 500 уток и 100 гусей, то вероятность подстрелить на охоте утку больше, чем вероятность подстрелить гуся.
   
3. 
   Если в мешке лежат 10 белых шаров и 3 черных, то вероятность достать черный шар меньше, чем вероятность вытаскивания белого.
   
4. 
   Если одна из сторон кубика будет более тяжелой, то вероятность выпадения этой стороны будет меньше, чем других сторон.
   

Как вычислить количество информации в сообщении о таком событии?

Для этого необходимо использовать следующую формулу, предложенную в 1948 г. американским математиком и инженером Клодом Шенноном: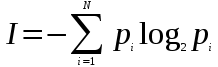

(4)

где I - количество информации;

N - количество возможных событий;

р_i - вероятность i-го события (р = К/N, К – величина, показывающая, сколько раз произошло интересующее нас событие).

Этот подход к определению количества информации называется вероятностным.

Для событий с равной вероятностью (р_i=1/N) количество информации рассчитывается по формуле: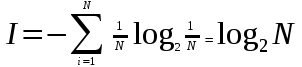

(5)
Количественная зависимость между вероятностью события (р) и количеством информации в сообщении о нем (i) выражается формулой:
I = log₂(1/p) (6)
Пример№1: В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика.

Решение

Т.к. количество шариков различных цветов неодинаково, то вероятности зрительных сообщений о цвете вынутого из мешочка шарика также различаются и равны количеству шариков данного цвета, деленному на общее количество шариков:

р_б = 0,1_; р_к = 0,2; р_с = 0,3; р_з = 0,4.

События неравновероятны, поэтому для определения количества информации, содержащегося в сообщении о цвете шарика воспользуемся формулой (4)

I = - (0,1^.log₂0,1 + 0,2^.log₂0,2 + 0,3^.log₂0,3 + 0,4^.log₂0,4) бит ≈ 1,85 бита

Количество информации, содержащееся в символе, которое определяется частотой его появления, равно: log₂ (1/р_i), бит и определяется по формуле (4), где р_i – вероятность (относительная частота) знака номер i данного алфавита из N знаков.

Ход работы:

1. 
   Решите задачи, используя вероятностный подход к измерению информации:
   

1. 
   В коробке 5 синих и 15 красных шариков. Определите количество информации в сообщении о том, что из коробки достали синий шарик;
   
2. 
   В коробке находятся кубики трех цветов: красного, желтого и зеленого. Причем желтых в два раза больше красных, а зеленых на 6 больше чем желтых. Сообщение о том, что из коробки случайно вытащили желтый кубик, содержало 2 бита информации. Определите количество зеленых кубиков;
   
3. 
   Студенты группы изучают один из трех языков: английский, немецкий или французский. Причем 12 студентов не учат английский. Сообщение, что случайно выбранный студент Петров изучает английский, несет log₂3 бит информации, а что Иванов изучает французский – 1 бит. Сколько студентов изучают немецкий язык?
   
4. 
   В колоде содержится 32 карты. Из колоды случайным образом вытянули туза, потом его положили обратно и перетасовали колоду. После этого из колоды опять вытянули этого же туза. Какое количество бит информации в сумме содержат эти два сообщения?
   
5. 
   В составе 16 вагонов, среди которых К – купейные, П – плацкартные и СВ – спальные. Сообщение о том, что ваш друг приезжает в СВ несет 3 бита информации. Определите, сколько в поезде вагонов СВ;
   
6. 
   Ученики группы, состоящего из 21 человека, изучают немецкий или французский языки. Сообщение о том, что ученик A изучает немецкий язык, несет log₂3 бит информации. Сколько человек изучают французский язык?
   
7. 
   В ящике лежат перчатки (белые и черные). Среди них – две пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет 4 бита информации. Сколько пар былых перчаток было в ящике?
   
8. 
   В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Определите количество шаров в корзине;
   
9. 
   В ведерке у рыбака караси и щуки. Щук в ведерке 3. Зрительное сообщение о том, что из ведра достали карася, несет 1 бит информации. Сколько всего рыб поймал рыбак?
   
10. 
    На автобусной остановке останавливаются два маршрута автобусов: № 5 и № 7. Ученику дано задание: определить, сколько информации содержит сообщение о том, что к остановке подошел автобус № 5, и сколько информации в сообщении о том, что подошел автобус № 7. Ученик провел исследование. В течение всего рабочего дня он подсчитал, что к остановке автобусы подходили 100 раз. Из них — 25 раз подходил автобус № 5 и 75 раз подходил автобус № 7. Сделав предположение, что с такой же частотой автобусы ходят и в другие дни, ученик вычислил вероятность появления на остановке автобуса № 5: p5= …, и вероятность появления автобуса № 7: p7 = ...
    

2. 
   Используя таблицу вероятности появления букв в русском тексте, посчитайте объем данного ниже сообщения:
   

Частота появления букв в русском тексте
Буква	Частота	Буква	Частота	Буква	Частота	Буква	Частота
пробел	0,175	о	0,090	е (ё)	0,072	а	0,062
и	0,062	т	0,053	н	0,053	с	0,045
р	0,040	в	0,038	л	0,035	к	0,028
м	0,026	д	0,025	п	0,023	у	0,021
я	0,018	ы	0,016	з	0,016	ь (ъ)	0,014
б	0,014	г	0,013	ч	0,012	й	0,010
х	0,009	ж	0,007	ю	0,006	ш	0,006
ц	0,004	щ	0,003	э	0,003	ф	0,002

Челябинск расположен на восточном склоне Уральских гор, южнее Екатеринбурга. Город находится на границе Урала и Сибири.

Стоит на реке Миасс, территорию города омывают Шершнёвское водохранилище и три озера: Смолино, Синеглазово, Первое. Рельеф города слабо холмистый на западе с постепенным понижением к востоку. Климат континентальный.

3. 
   Полученные результаты занесите в итоговую таблицу.
   
4. 
   Ответьте на контрольные вопросы:
   

• 
  Приведите примеры событий с разной вероятностью реализации;
  
• 
  Как вычислить количество информации в сообщении о таких событиях?
  

5. 
   Оформите и сдайте отчет преподавателю.