5485756_Доп_2. Практическая работа 2 Моделирование случайных величин с заданным законом распределения Вариант 1 Проверил 2020
 Скачать 332 Kb. Скачать 332 Kb.
|
|
Министерство науки и высшего образования РФ Практическая работа №2 «Моделирование случайных величин с заданным законом распределения» Вариант №1 Выполнил: Проверил: 2020 Задание 1. Необходимо выполнить следующие задания: для каждого из следующих трех видов распределений (параметры распределений взять из п.2 данной работы): нормального N(m, σ) (σ > 0), равномерного R(a, b) (a < b), экспоненциальногоE(λ) (λ > 0) написать программу вывода в графическом окне графиков функций распределения с использованием функций Excel. 2. Написать программу, осуществляющую моделирование массивов объемом 300 для законов распределения: нормального, равномерного, экспоненциального. Для каждого из этих массивов вывести в графическом окне график гистограммы относительных частот группированной выборки (шесть – восемь интервалов группировки). Продемонстрировать полученные результаты преподавателю. Исходные данные по варианту Параметры моделируемых массивов: для нормального распределения N(m, σ) (σ> 0): m=1, σ= 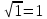 ; ;для равномерного распределения R(a ;b) (a для экспоненциального распределения E(λ)( λ> 0 ): 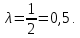 . .Основные определения и алгоритмы моделирования случайных величин Нормальное распределение, также называемое распределением Гаусса – распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса: 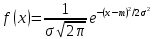 Математическое ожидание 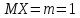 . .Дисперсия  . .Коэффициент асимметрии: 0; Коэффициент эксцесса: 0. Аналитическое выражение для моделирования нормальной СВ имеет вид:  где α1 и α2 - независимые равномерно распределенные случайные числа на интервале [0; 1), m – математическое ожидание СВ, σ – среднеквадратическое отклонение. Равномерное распределение – распределение случайной вещественной величины, принимающей значения, принадлежащие интервалу [a, b], характеризующееся тем, что плотность вероятности на этом интервале постоянна. 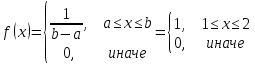 Функция распределения: 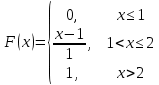 Математическое ожидание  . .Дисперсия 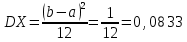 . .Коэффициент асимметрии: 0; Коэффициент эксцесса: -1,2. Аналитическое выражение для моделирования имеет вид: 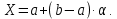 где α - независимые равномерно распределенные случайные величины на интервале [0; 1). Экспоненциальное распределение - абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события. Плотность распределения 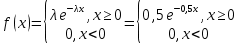 Функция распределения: 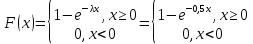 Математическое ожидание  . .Дисперсия 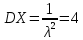 . .Коэффициент асимметрии: 2; Коэффициент эксцесса: 6. Аналитическое выражение для моделирования имеет вид: 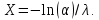 где α - независимые равномерно распределенные случайные числа на интервале [0; 1), Основные определения Случайная величина – величина которая при испытаниях принимает одно из возможных значений, наперед неизвестно какое. Бывают дискретными и непрерывными. Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления. Сумма всех вероятностей Σpi = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi). Функция распределения – функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее или равное х, где х – произвольное действительное число. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x). Смысл плотности распределения состоит в том, что она показывает, как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов. Коэффициент асимметрии – числовая характеризующая степени несимметричности распределения данной случайной величины. Коэффициент эксцесса (коэффициент островершинности) – мера остроты пика распределения случайной величины. Графики и характеристики в Excel Функция СЛЧИС, генерирующая случайные последовательности, равномерно распределенные на отрезке [0,1]. Ее синтаксис СЛЧИС() и она не имеет аргументов – располагаем выборку в столбце А. Далее согласно алгоритму генерируем выборку из заданного распределения объёмом 300 единиц. Нормальное распределение Выборка из нормального распределения расположена в столбце С:  Для построения плотности и функции распределения использовали функцию НОРМ.РАСП. Например, J2 = =НОРМ.РАСП($H2;F$1;F$2;ЛОЖЬ); I2 =НОРМ.РАСП(H2;$F$1;$F$2;ИСТИНА)  Рис. Функция и плотность распределения Для построения гистограммы вычисляем частоты попадания в каждый интервал. 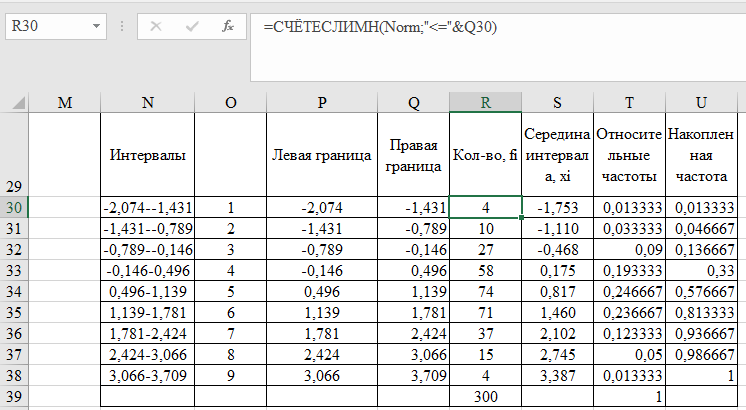 Здесь Norm – именованный диапазон с нормально распределенной СВ. 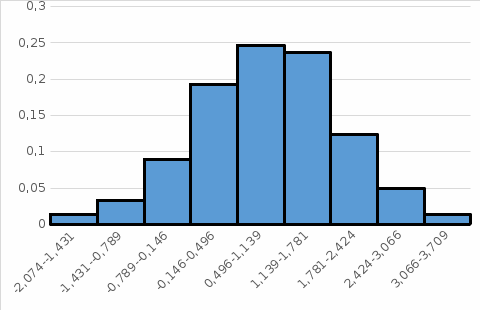 Рис. Гистограмма относительных частот Случайные числа для выборок объемом 100, 1000, 10000, 100000 расположены в столбцах A-G. Вычисляем их характеристики: 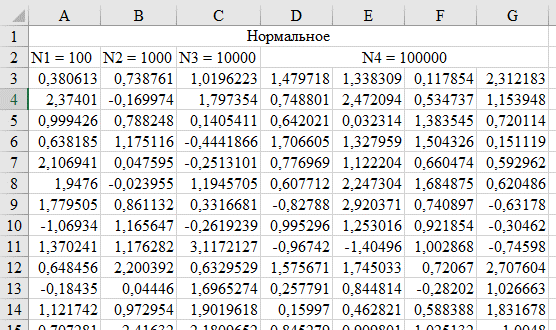 Графики зависимости оценки мат. ожидания, дисперсии, коэффициента асимметрии и эксцесса от длины выборки: 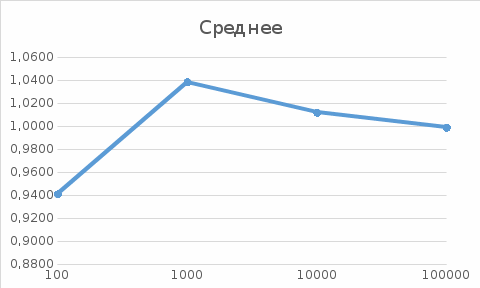  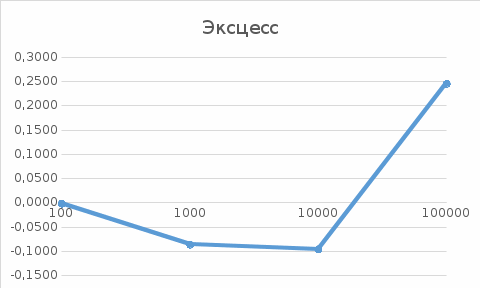 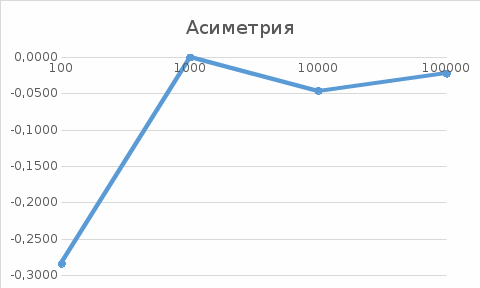
Равномерное распределение Фрагмент выборки (столбец B): 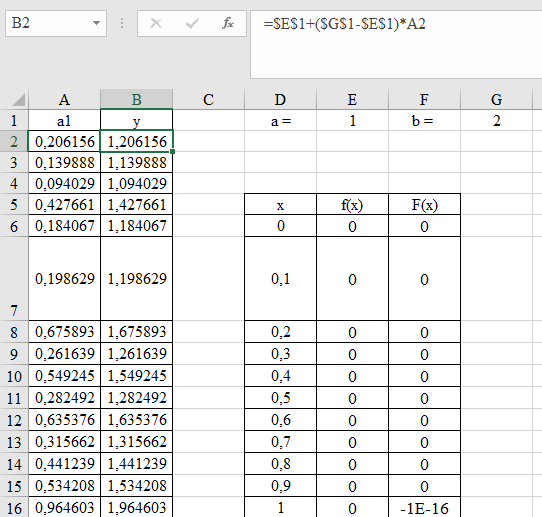 Для построения плотности и функции распределения используем аналитическое выражение. Например, E6=ЕСЛИ(И(D6>$E$1;D6<$G$1);1/($G$1-$E$1);0) F6=ЕСЛИ(И(D6>=$E$1;D6<$G$1);(D6-$E$1)/($G$1-$E$1);ЕСЛИ(D6<$E$1;0;1))  Рис. Функция и плотность распределения Для построения гистограммы вычисляем частоты попадания в каждый интервал. 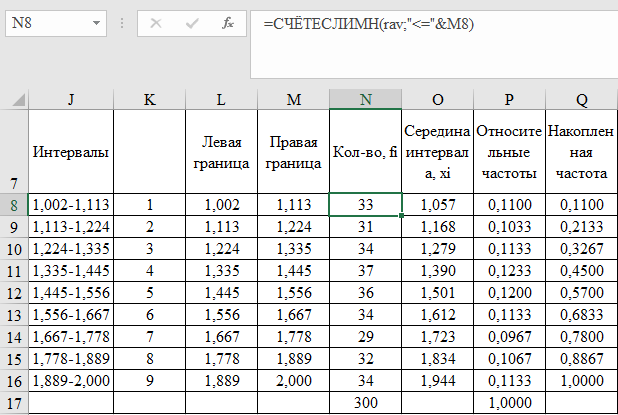 Здесь rav – именованный диапазон с равномерно распределенной СВ. 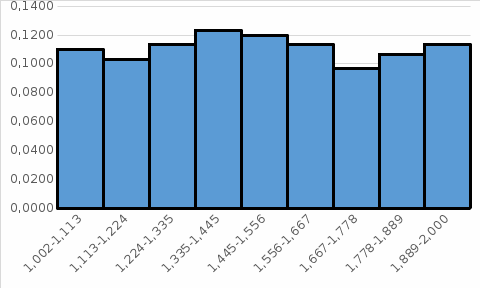 Рис. Гистограмма относительных частот Случайные числа для выборок объемом 100, 1000, 10000, 100000 расположены в столбцах A-G. Характеристики: 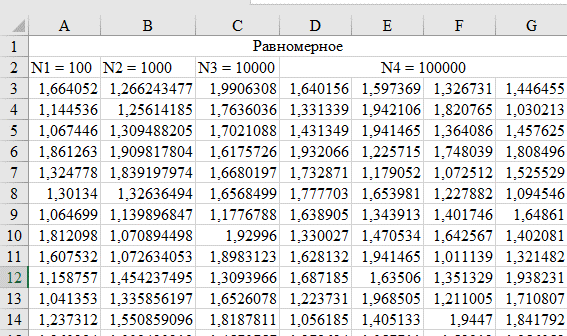
Графики зависимости оценки мат. ожидания, дисперсии, коэффициента асимметрии и эксцесса от длины выборки:  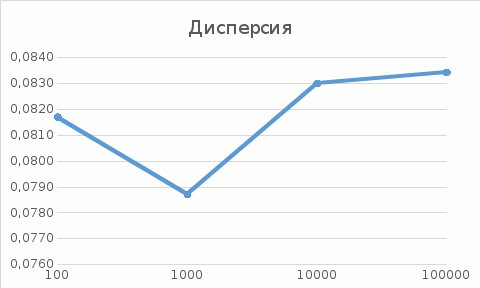 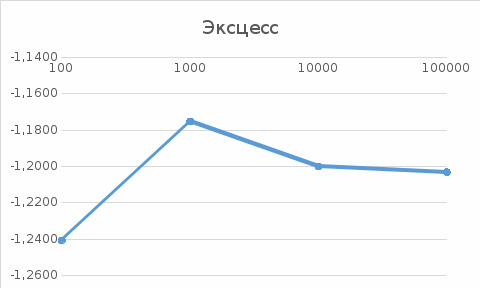 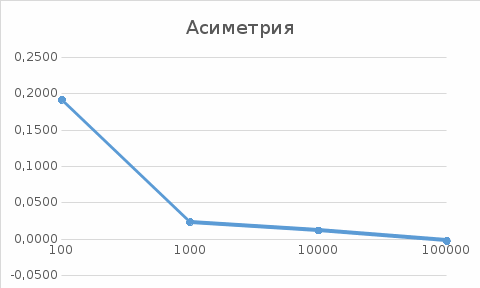 Экспоненциальное распределение Фрагмент выборки (столбец B): 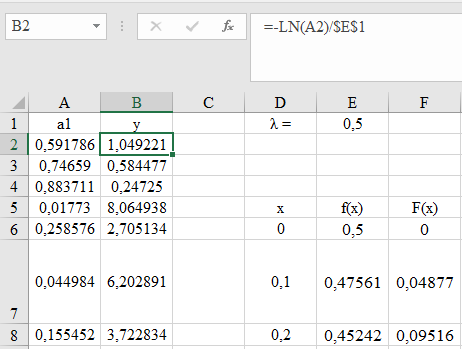 Для построения плотности и функции распределения использовали функцию ЭКСП.РАСП. Например, E6= ЭКСП.РАСП(D6;$E$1;ЛОЖЬ); F6= ЭКСП.РАСП(D6;$E$1;ИСТИНА) 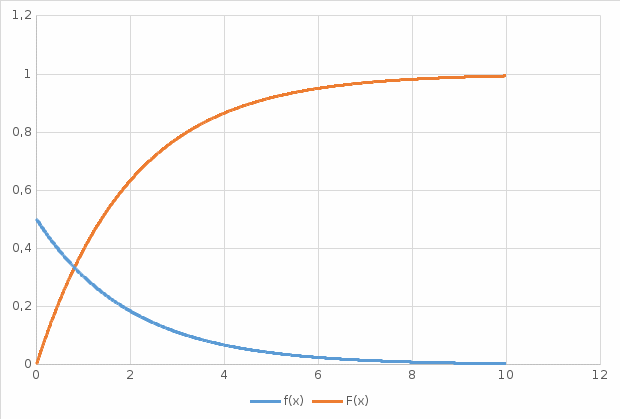 Рис. Функция и плотность распределения Для построения гистограммы вычисляем частоты попадания в каждый интервал.
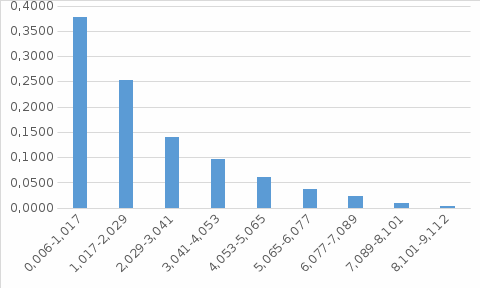 Рис. Гистограмма относительных частот Случайные числа в количестве 100000 штук получим с помощью алгоритма Y  где x - независимые равномерно распределенные случайные числа на интервале [0; 1). x располагаются в столбце A, а где x - независимые равномерно распределенные случайные числа на интервале [0; 1). x располагаются в столбце A, а в столбце B-H. в столбце B-H.Характеристики: 
Графики зависимости оценки мат. ожидания, дисперсии, коэффициента асимметрии и эксцесса от длины выборки:   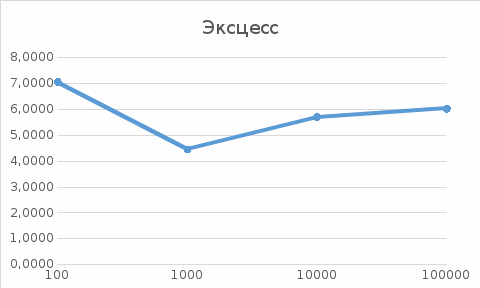  Таблица сравнения теоретических числовых характеристик СВ и характеристик, полученных по моделируемой выборке
Таким образом, с ростом N выборочные значения приближаются к теоретическим. Полученные гистограммы распределений приближаются к теоретическим плотностям распределений, т.е. разработанные датчики случайных чисел реализованы верно. Изученные возможности пакета Excel позволяют моделировать и анализировать одномерные случайные величины. Для основных законов распределения имеются встроенные функции, остальные законы распределения можно получить с помощью самостоятельно написанных алгоритмов. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
