Практическая работа №2. Практическая работа 2 Вариант 75 Задача 7. 1
 Скачать 136.36 Kb. Скачать 136.36 Kb.
|
|
Ответ: количество теплоты, передаваемой через стенку составляет 800 Вт., температуры на границах слоев изоляции 179,928 0С и 39,678 0С. Задача №8.1 Определить конвективный тепловой поток от крыши здания площадью F м2 и температурой tк в окружающий воздух с температурой tв, если в безветренную погоду коэффициент теплоотдачи равен в1. Насколько изменится тепловой поток в ветреный день при коэффициенте теплоотдачи в2.
Решение: Конвективный теплообмен- это процесс переноса теплоты в жидкой и газообразной среде с неоднородным распределением температуры Процесс теплообмена между поверхностью твердого тела и жидкостью или газом называется теплоотдачей, а поверхность твердого тела, через которую переносится теплота - поверхностью теплообмена. Основной закон конвективного теплообмена - закон Ньютона - Рихмана: Q = α * F * (tc - tж), где Q - тепловой поток; F - площадь поверхности теплообмена, м2; tc и tж - температуры поверхности твердого тела (стенки) и теплоносителя, соответственно, 0С; - коэффициент теплоотдачи, Вт/(м2К). Он характеризует интенсивность процесса теплоотдачи. Коэффициент теплоотдачи - это тепловой поток, передаваемый в единицу времени через единицу площади поверхности при разности температур поверхности и жидкости в один градус. Так как, известно численное значение коэффициента теплоотдачи , можно сразу воспользоваться уравнением Ньютона - Рихмана и определить требуемую величину. Определяем конвективный тепловой поток от крыши здания в безветренную погоду: Q1 = в1 * F * (tк – tв) = 4,5 * 700 * (45+8) = 166950 Вт = 166.95 кВт Определяем конвективный тепловой поток от крыши здания в ветреный день: Q2 = в2 * F * (tк – tв) = 50 * 700 * (45+8) = 1855000 Вт = 1855 кВт Определяем насколько изменится тепловой поток в ветреный день по сравнению с безветренной погодой: Q2 - Q1 = 1855 - 166.95 = 1688,05 кВт или (Q2 - Q1) / Q1 = (1855 - 166.95) / 166.95 *100% = 1011,1% Ответ: на 1688,05 кВт или 1011,1% изменится тепловой поток в ветреный день. Задача №8.10 Определить коэффициент теплоотдачи и количество переданной теплоты при течении воды в трубе диаметром d и длиной l, если расход воды составляет v л/ч, средняя температура воды tж, температура стенки трубы tс.
Решение: Физические параметры воды при определяющей температуре, равной 81 0С (приложение 5 Таблица П.5.2 - Физические параметры воды на линии насыщения): tводы = 81 0С = 67,5 * 10-2 Вт/(м·0С) = 0,365 *10-6 м2/сек Рr1 = 2,21 Критерий Prс находим по тому же приложению, но при температуре стенки 36 0С: Рrс = 4,865 Рассчитаем среднюю скорость течения воды w по трубе: w = 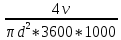 = = 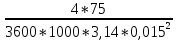 = 0,118 м/с = 0,118 м/сЗначение критерия Рейнольдса находим по уравнению: Red = 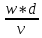 = = 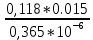 = 4849,3 = 4849,3где w - скорость движения жидкости, м/с; d - определяющий размер, м; - коэффициент кинематической вязкости, м2/с. Re представляет собой безразмерную скорость потока, характеризует гидродинамический режим потока. Re выражает отношение сил инерции (скоростного напора) к силам вязкого трения. При течении жидкости в трубах: Re 2300 - ламинарный режим, Re = 2300104 - переходный режим, Re 104 - турбулентный режим. В нашем случае, режим движения – переходный. Для расчета выбираем формулу - поток в трубе при Re = 2320…104: Nuж = K0 * Рrж 0,43 * 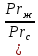 )0,25 * )0,25 *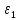 * *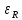 K0 = 5,888 ε1=1,1675 – поправочный коэффициент для коротких труб при l < 50d (l/d = 46,7); εR – поправка для изогнутых труб, т.к. труба прямая, то εR=1. Тогда: Nuж = 5,888 * 2,210,43 * 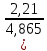 )0,25 * 1,1675 * 1 = 7,94 )0,25 * 1,1675 * 1 = 7,94Коэффициент теплоотдачи соответственно равен: α = (Nuж * ) / d = (7,94 * 67,5 * 10-2 )/0,015 = 357,3 Вт / м2 *К Тогда, количество переданной теплоты при течении воды в трубе: Q = α * π *d *l * (tж – tс) = 357,3 *3,14 * 0,015*0,7 * (81-36) = 530,1 Вт Ответ: коэффициент теплоотдачи 357,3 Вт / м2 *К, количество переданной теплоты при течении воды в трубе 530,1 Вт. Задача №8.12 Определить коэффициент теплоотдачи и линейную плотность теплового потока в поперечном потоке воздуха для трубы диаметром d мм, если температура ее поверхности tc, температура воздуха tвозд и скорость ветра w м/с.
Решение: Физические параметры воздуха при определяющей температуре, равной -35 0С (приложение 5 Таблица П.5.1 - Физические параметры сухого воздуха при давлении 760 мм.рт.ст.): tвозд = -35 оС ·10-2 = 2,16 * 10-2 Вт/(м·0С) ·10-6 = 10,42 * 10-6 м2/сек Рr1 = 0,7255 Критерий Prс находим по тому же приложению, но при температуре стенки 55 0С: Рrс = 0,697 Значение критерия Рейнольдса находим по уравнению: Red = 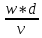 = = 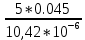 = 21593 = 21593 где w - скорость движения жидкости (ветра), м/с; d - определяющий размер, м; - коэффициент кинематической вязкости, м2/с. Re представляет собой безразмерную скорость потока, характеризует гидродинамический режим потока. Re выражает отношение сил инерции (скоростного напора) к силам вязкого трения. При течении жидкости в трубах: Re 2300 - ламинарный режим, Re = 2300104 - переходный режим, Re 104 - турбулентный режим. В нашем случае, режим движения – турбулентный. Для расчета выбираем формулу - процесс теплообмена при поперечном обтекании одиночной трубы при Re > 103: Nuж = 0,216 * Reж0,6 = 0,216 * 215930,6 = 86,1 Коэффициент теплоотдачи соответственно равен: α = (Nuж * ) / d = (86,1*2,16 * 10-2) / 0,035 = 53,136 Вт/(м2·К); где α - коэффициент теплоотдачи, Вт/(м2∙К); d - определяющий размер, м; - коэффициент теплопроводности, Вт/(м∙К). Линейная плотность теплового потока в поперечном потоке воздуха (тепловой поток на единицу длины трубы): ql = α * π *d * (tc – tвозд) = 53,136 * 3,14 * 0,035 * (55+35) = 525,6 Вт/м Ответ: коэффициент теплоотдачи 53,136 Вт/(м2·К); Линейная плотность теплового потока в поперечном потоке воздуха 525,6 Вт/м. Задача №8.15 Труба внешним диаметром d = 25 мм (0,025 м) охлаждается поперечным потоком масла. Скорость движения и средняя температура масла равны соответственно: w = 1,5 м/с и tж= 18°C. Определить, какую температуру поверхности трубы необходимо поддерживать, чтобы плотность теплового потока составляла q = 40 кВт/м2, и каково при этом будет значение коэффициента теплоотдачи? Марка масла МС-20. Решение: Физические параметры масла марки МК при заданной температуре (приложение 5 Таблица П.5.6 - Физические свойства масла МК в зависимости от температуры): tвозд = 18 оС = 0,1465 Вт/(м·0С) = 1514* 10-6 м2/сек Рr1 = 15800 Определяем режим движения масла марки МК: 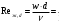 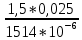 = 24,8 = 24,8Так как число Рейнольдcа находится в пределах 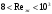 , то - ламинарный режим. , то - ламинарный режим.Для расчета выбираем формулу - процесс теплообмена при поперечном обтекании одиночной трубы капельной жидкостью при Re = 5…2·106: 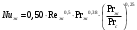 В формулу входит число Прандтля для масла, взятое при температуре стенки. Поэтому задачу приходится решать либо методом последовательных приближений, либо графическим методом. Используем последний. Зададимся тремя значениями температуры стенки: tC1 = 40°C; tC2 = 60°С и tC3 = 80°С, вычислим плотности теплового потока при этих температурах и построим график q = f(tC). Задавшись tC1 = 40°C, по указанной выше формуле рассчитаем коэффициент теплоотдачи. При температуре 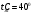 , ,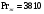 ; ; 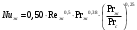 = 0,50 * 24,80,5 *158000,38 *(15800/3810)0,25 = 140 = 0,50 * 24,80,5 *158000,38 *(15800/3810)0,25 = 140 Коэффициент теплоотдачи соответственно равен: 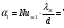 140 * (0,1465/0,025) = 820,4 Вт/м2∙К. 140 * (0,1465/0,025) = 820,4 Вт/м2∙К.Плотность теплового потока при tC1 = 40°C 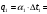 820,4 * (40-18) = 18048,8 Вт/м2. 820,4 * (40-18) = 18048,8 Вт/м2. При температуре tC2 = 60°С значение коэффициента теплоотдачи будет отличаться от α1 только в связи с изменением PrC, поэтому 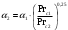 и и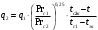 При tC2 = 60°C, РгC2 = 1320 α 2 = 820,4 * (3810 / 1320)0,25 = 1069,3 Вт/м2∙К. q2 = 18048,8 *(3810 / 1320)0,25 * 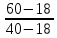 = 44912 Вт/м2. = 44912 Вт/м2.При tC3 = 80°С, РгC3 = 591 и q3 = 18048,8 * (1320/591)0,25* 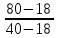 = 62182 Вт/м2. = 62182 Вт/м2.По вычисленным значениям q строим график q=f(tC) (рисунок 3).  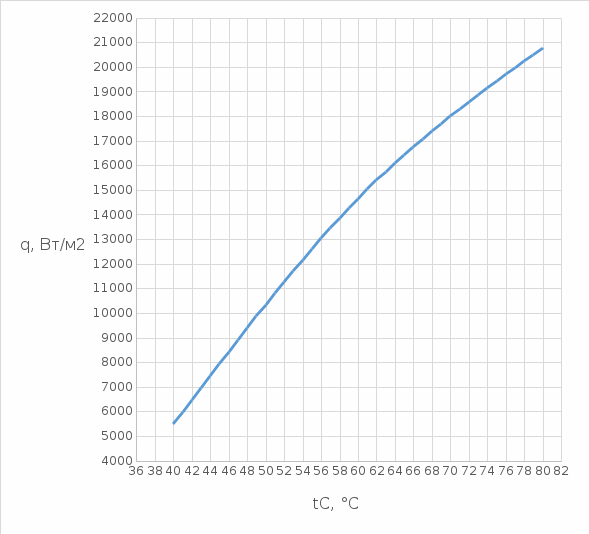 Рисунок 3 - Зависимость q=f(tC) По графику находим, что при заданном значении q = 15∙103 Вт/м2 температура стенки tC = 61°С. При найденной температуре tC = 61°С вычисляем коэффициент теплоотдачи. При tC = 61°С, РгC = 1273,8. Тогда 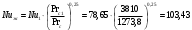 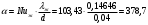 Вт/м2∙К. Вт/м2∙К. |
