Решение_Контр. страхование. Практическая работа 3 Расчет тарифов страхования (методика 1)
 Скачать 87.14 Kb. Скачать 87.14 Kb.
|
Практическая работа 3Расчет тарифов страхования (методика 1)Цель работы: развить навыки расчета тарифов по массовым рисковым видам страхования Теоретические основы Тарифная ставка – ставка страхового платежа предназначена для возмещения ущерба, причинённого застрахованному имуществу страховым событием, а также для других расходов страховых организаций. Тарифная ставка представляет собой годовой платёж со 100 руб. страховой суммы, выражается в денежных единицах или в %. По обязательным видам страхования величина страхового тарифа определяется законодательством, а по добровольным видам страхования - страховой организацией. Предлагаемая методика пригодна для расчета тарифных ставок для рисковых видов страхования и применима при следующих условиях: 1) существует статистика либо какая-то другая информация по рассматриваемому виду страхования, что позволяет оценить следующие величины: q - вероятность наступления страхового случая по одному договору страхования, S - среднюю страховую сумму по одному договору страхования, Sв - среднее возмещение по одному договору страхования при наступлении страхового случая; 2) предполагается, что не будет опустошительных событий, когда одно событие влечет за собой несколько страховых случаев; 3) расчет тарифов проводится при заранее известном количестве договоров n, которые предполагается заключить со страхователями. При наличии статистики по рассматриваемому виду страхования за величины q, S, Sв принимаются оценки их значений: 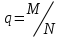 (7.8.1) (7.8.1)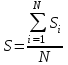 (7.8.2) (7.8.2)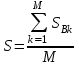 (7.8.3) (7.8.3)где N - общее количество договоров, заключенных за некоторый период времени в прошлом; M - количество страховых случаев в N договорах; Si - страховая сумма при заключении i-го договора, i = 1, 2, ..., N; Sвk - страховое возмещение при k-м страховом случае, k = 1, 2, ..., M. При страховании по новым видам рисков при отсутствии фактических данных о результатах проведения страховых операций, т.е. статистики по величинам q, S и Sв, эти величины могут оцениваться экспертным методом либо в качестве них могут использоваться значения показателей - аналогов. Нетто - ставка Tn состоит из двух частей - основной части Tо и рисковой надбавки Tр: Tn = Tо + Tр. (7.8.4) Основная часть нетто - ставки (Tо) соответствует средним выплатам страховщика, зависящим от вероятности наступления страхового случая q, средней страховой суммы S и среднего возмещения Sв. Основная часть нетто - ставки со 100 руб. страховой суммы рассчитывается по формуле: 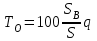 (руб.) (7.8.5) (руб.) (7.8.5)Рисковая надбавка Tр вводится для того, чтобы учесть вероятные превышения количества страховых случаев относительно их среднего значения. Кроме q, S и Sв, рисковая надбавка зависит еще от трех параметров: n - количества договоров, отнесенных к периоду времени, на который проводится страхование, среднего разброса возмещений Rв и гарантии гамма - требуемой вероятности, с которой собранных взносов должно хватить на выплату возмещения по страховым случаям. Возможны два варианта расчета рисковой надбавки. 1. Рисковая надбавка может быть рассчитана для каждого риска. В этом случае 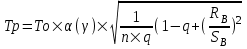 (7.8.6) (7.8.6)где альфа (гамма) - коэффициент, который зависит от гарантии безопасности гамма. Его значение может быть взято из таблицы 7.8.1. Таблица 7.8.1 Гарантия безопасности
Rв - среднеквадратическое отклонение возмещений при наступлении страховых случаев. При наличии статистики выплат страховых возмещений дисперсия выплат R2В оценивается следующим в образом: 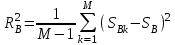 (7.8.7) (7.8.7)где Sвk - страховое возмещение при k-м страховом случае, k = 1, 2, ..., M; M - количество страховых случаев в N договорах; Sв - среднее возмещение по одному договору страхования при наступлении страхового случая. Если у страховой организации нет данных о величине Rв, допускается вычисление рисковой надбавки по формуле: 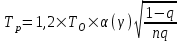 (7.8.8) (7.8.8)2. В том случае, когда страховая организация проводит страхование по нескольким видам рисков (j = 1, 2, ..., m), рисковая надбавка может быть рассчитана по всему страховому портфелю, что позволяет несколько уменьшить ее размер: 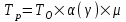 (7.8.9) (7.8.9)где 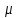 - коэффициент вариации страхового возмещения, который соответствует отношению среднеквадратического отклонения к ожидаемым выплатам страхового возмещения. - коэффициент вариации страхового возмещения, который соответствует отношению среднеквадратического отклонения к ожидаемым выплатам страхового возмещения. Если о величинах q, S, Sв нет достоверной информации, то рекомендуется брать 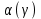 альфа (гамма) = 3. альфа (гамма) = 3.Брутто - ставка Tб рассчитывается по формуле: 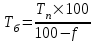 (7.8.10) (7.8.10)где Tn - нетто - ставка; f (%) - доля нагрузки в общей тарифной ставке. Задание для самостоятельной работы На основе данных варианта (таблица 7.8.1) рассчитать брутто-ставку страхового тарифа по массовым рисковым видам страхования. Таблица 7.8.1 Варианты для самостоятельной работы
Решение: 1) Находим вероятность наступления страхового случая по одному договору страхования: 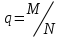 , ,где N – общее количество договоров, заключенных за некоторый период времени в прошлом; M – количество страховых случаев в N договорах. 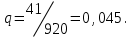 2) Находим основную часть нетто- ставки со 100 руб. страховой суммы: 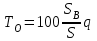 , ,S – средняя страховая сумма по одному договору страхования; Sв – среднее возмещение по одному договору страхования при наступлении страхового случая. 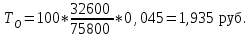 3) Находим рисковую надбавку, используя следующую формулу: 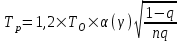 , ,где 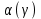 - коэффициент, который зависит от гарантии безопасности гамма - коэффициент, который зависит от гарантии безопасности гамма 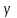 (выбираем по таблице 7.8.1; (выбираем по таблице 7.8.1;n – количество договоров, отнесенных к периоду времени, на который проводится страхование. 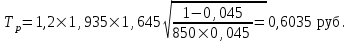 4) Нетто-ставка Tn состоит из двух частей – основной части Tо и рисковой надбавки Tр: Tn = Tо + Tр Tn = 1,935 + 0,6035= 2,5385 руб. 5) Брутто-ставка Tб рассчитывается по формуле: 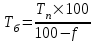 , ,где f (%) – доля нагрузки в общей тарифной ставке. 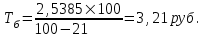 , ,Таким образом, брутто-ставка страхового тарифа по массовым рисковым видам страхования равна 3,21 руб. со 100 руб. страховой суммы. Практическая работа 4Расчет тарифов по видам страхования (методика 2)Цель работы: развить навыки расчета тарифов по рисковым видам страхования Теоретические основы Данную методику целесообразно использовать по видам страхования на основе имеющейся страховой статистики за определенный период времени или при отсутствии таковой использовать статистическую информационную базу (демографическая статистика, смертность, инвалидность, производственный травматизм и т.д.). Определение страхового тарифа на основе страховой статистики за несколько лет осуществляется с учетом прогнозируемого уровня убыточности страховой суммы на следующий год. Предлагаемая методика применима при следующих условиях: 1) имеется информация о сумме страховых возмещений и совокупной страховой сумме по рискам, принятым на страхование, за ряд лет; 2) зависимость убыточности от времени близка к линейной. Расчет нетто - ставки производится в следующей последовательности: а) по каждому году рассчитывается фактическая убыточность страховой суммы (y) как отношение страхового возмещения к общей страховой сумме застрахованных рисков (Sв / S) б) на основании полученного ряда исходных данных рассчитывается прогнозируемый уровень убыточности страховой суммы, для чего используется модель линейного тренда, согласно которой фактические данные по убыточности страховой суммы выравниваются на основе линейного уравнения: 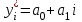 (7.9.1) (7.9.1)где yi* - выравненный показатель убыточности страховой суммы, a0, a1 - параметры линейного тренда, i - порядковый номер соответствующего года. Параметры линейного тренда можно определить методом наименьших квадратов, решив следующую систему уравнений с двумя неизвестными: 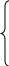 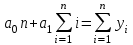 (7.9.2) (7.9.2)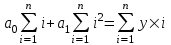 где n - число анализируемых лет. Коэффициенты данной системы уравнений находятся с помощью таблицы 7.9.1: Таблица 7.9.1 Расчет коэффициентов
Подставив полученные данные в систему уравнений, получим: a0 x 5 + a1 x 15 = 1,48, a0 x 15 + a1 x 55 = 4,96 Решив систему уравнений, получаем следующие значения: a0 = 0,14, a1 = 0,052, на основании которых можно определить выравненную убыточность по годам, подставляя необходимые данные в уравнение. Таким образом, ожидаемая убыточность на 1993 год с учетом тренда исходных данных составит: y6 = a0 + a1 x 6, y6 = 0,14 + 0,052 x 6 = 0,452 руб. со 100 руб. страховой суммы, т.е. это и является основной частью нетто - ставки; в) для определения рисковой надбавки необходимо по следующей формуле рассчитать среднее квадратическое отклонение фактических значений убыточности от выравненных значений: 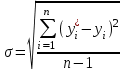 (7.9.4) (7.9.4)Используемые для определения рисковой надбавки показатели приведены в таблице 7.9.2: Таблица 7.9.2 Рисковые надбавки
Подставив рассчитанные показатели в формулу (7.9.4), получим: 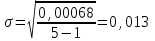 г) нетто - ставка рассчитывается следующим образом: Tn = y6 + β (γ; n) x σ, где β (γ; n) - коэффициент, используемый для исчисления размера рисковой надбавки. Величина β (γ; n) зависит от заданной гарантии безопасности γ (той вероятности, с которой собранных взносов хватит на выплаты страховых возмещений) и n - числа анализируемых лет и может быть взята из таблицы 7.9.3. Таблица 7.9.3 Коэффициент, используемый для исчисления размера рисковой надбавки
Допустим, страховая компания считает необходимым с уровнем вероятности γ = 0,9 быть уверена в том, что собранной суммы взносов будет достаточно для выплаты страховых возмещений. Тогда из таблицы 4 при γ = 0,9 для n = 5, бета = 1,984. Нетто - ставка со 100 руб. страховой суммы Tn = 0,452 + 1,984 x 0,013 = 0,48 (руб.). Брутто - ставка (Tб) определяется по следующей формуле: 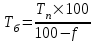 (7.9.5) (7.9.5)где Tn - нетто - ставка, f(%) - доля нагрузки в общей тарифной ставке. При условии, что нагрузка определена страховой организацией в размере 30% от брутто - ставки, рассчитывается брутто - ставка: 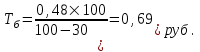 Брутто - ставка со 100 руб. страховой суммы равна 0,69 руб. Задание для самостоятельной работы На основе данных варианта (таблица 7.9.4) рассчитать брутто-ставку страхового тарифа по массовым рисковым видам страхования. Таблица 7.9.4 Варианты для самостоятельной работы
Решение: 1) На основании ряда исходных данных рассчитываем прогнозируемый уровень убыточности страховой суммы, для чего используем модель линейного тренда, согласно которой фактические данные по убыточности страховой суммы выравниваются на основе линейного уравнения: 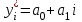 где yi* – выравненный показатель убыточности страховой суммы, a0, a1 – параметры линейного тренда, i – порядковый номер соответствующего года. Параметры линейного тренда можно определить методом наименьших квадратов, решив следующую систему уравнений с двумя неизвестными: 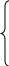 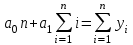 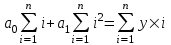 , ,где n – число анализируемых лет. 2) Запишем исходные данные в удобном для расчетов виде, а также найдем коэффициенты данной системы уравнений. Результаты представлены в таблице 7.9.5. Таблица 7.9.5 Расчет коэффициентов
Подставив полученные данные в систему уравнений, получим: a0*6 + a1*21 = 1,25, a0*21 + a1*91 = 4,17. Решив систему уравнений, получаем следующие значения: a0 = 0,25, a1 = - 0,0117, на основании которых можно определить выравненную убыточность по годам, подставляя необходимые данные в линейное уравнение. Таким образом, ожидаемая убыточность на 7 год с учетом тренда исходных данных составит: y7 = a0 + a1*7, y7 = 0,25 – 0,0117*7 = 0,1681 руб. со 100 руб. страховой суммы, т. е. это и является основной частью нетто-ставки. 3) Для определения рисковой надбавки рассчитаем среднее квадратическое отклонение фактических значений убыточности от выравненных значений: 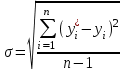 Используемые для определения рисковой надбавки показатели приведены в таблице 7.9.6. Таблица 7.9.6 Рисковые надбавки
Подставив рассчитанные показатели в формулу для рисковой надбавки, получим: 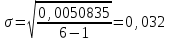 . .4) Нетто-ставку рассчитываем следующим образом: Tn = y7 + β (γ; n) * σ, где β (γ; n) – коэффициент, используемый для исчисления размера рисковой надбавки. В данном случае β (γ; n) = 0,8 (из исходных данных). Нетто-ставка со 100 руб. страховой суммы составит: Tn = 0,1681 + 0,8*0,032= 0,1937 (руб.). Брутто-ставка (Tб) определяется по следующей формуле: 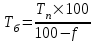 , ,где Tn – нетто-ставка, f (%) – доля нагрузки в общей тарифной ставке. По условию нагрузка определена страховой организацией в размере 30% от брутто-ставки, тогда брутто-ставка составит: 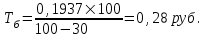 Таким образом, брутто-ставка со 100 руб. страховой суммы равна 0,28 руб. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 γ
γ