Двоичные линейные блоковые коды. Двоичные линейные блоковые коды- методичка. Практическая работа Линейные блочные коды
 Скачать 112 Kb. Скачать 112 Kb.
|
|
Практическая работа Линейные блочные коды. Выполнить описанные действия для двоичного линейного блочного кода, обладающего заданной порождающей (или проверочной) матрицей. A. Вычислить длину, размерность и скорость кода. B. Вычислить количество кодовых слов. C. Найти порождающую (проверочную) матрицу кода. D. Выписать все информационные и соответствующие им кодовые слова. E. Построить стандартную декодирующую таблицу этого кода. Сколько смежных классов у этого кода? Перечислить лидеров этих классов. F. Рассчитать синдром для принятого из зашумленного канала вектора с и декодировать его, используя стандартную таблицу. G. Вычислить способности рассматриваемого кода по исправлению и обнаружению ошибок? Рассмотрим двоичный линейный блоковый (n,k)-код С с порождающей матрицей G (размером k ? n) и проверочной матрицей Н (размером (n-k)? n). 2.1. Двоичный (n,k)-код С задается как отображение множества двоичных векторов длины k во м 2.2. Кодовое слово v С (длины n) и информационное слово u (длины k) связаны соотношением: v=u*G. 2.3. Любое кодовое слово v С удовлетворяет условию vHT=0. 2.4. Произвольная порождающая матрица G линейного блокового (n,k)-кода может быть преобразована к систематической форме Gsys с помощью элементарных операций и перестановок столбцов матрицы. Матрица Gsys состоит из двух подматриц: k * k единичной матрицы, обозначаемой Ik и k x (n-k) проверочной подматрицы Р. Таким образом, так как GHT=0, то отсюда следует, что систематическая форма проверочной матрицы имеет вид: 2.5. Стандартная декодирующая таблица содержит 2n-k строк и 2k+1 столбцов. Процедура построения стандартной таблицы состоит в следующем. А) Правые 2k столбцов заголовка таблицы заполним информационными словами, начиная с нулевого слова. Правые 2k столбцов первой строки заполняем кодовыми словами кода С (соответствующими информационным словам, указанными в заголовке) В первую ячейку первого столбца записываем нулевой синдром. Полагаем j=0. В) Для j=j+1, находим шумовое слово ej V2 минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Соответствующий синдром sj=ejHT записываем в первый (крайний левый) столбец j-той строки. В оставшиеся 2k ячейки этой строки запишем суммы ej и кодовых слов uj. Отметим, что в случае кода с неравной защитой от ошибок, возможно совпадение значений синдрома для различных значений шумовых слов. При таком совпадении необходимо оставить только один вектор ej из векторов, имеющих одинаковые значения синдрома. С) Повторяем шаг В процедуры пока j<2n-k, т.е. пока все вектора из V2 не окажутся включенными в таблицу. Анализируя построенную таблицу нетрудно заметить, что все элементы одной и той же строки имеют один и тот же синдром. Элементы каждой строки представляют собой смежный класс кода С. А соответствующий вектор ej называется лидером смежного класса. 2.6. В двоичном пространстве V2 расстояние Хемминга определяется как число позиций, на которых два вектора не совпадают. Пусть x1=(x1,0, x1,1, …, x1,n-1) и x2=(x2,0, x2,1, …, x2,n-1) два вектора в V2. Тогда расстояние Хемминга между векторами x1 и x2, обозначаемое как dh(x1,x2), равно где через |A| обозначено число элементов в А. 2.7. Весом Хемминга слова w из пространства V2 называют число wth(w) его ненулевых позиций, иными словами wth(w) - это расстояние Хемминга между нулевым словом и словом w. 2.8. Для заданного кода С минимальное Хеммингово расстояние dmin определяется как минимум Хеммингова расстояния по всем возможным парам различных кодовых слов Согласно этой формуле, для определения минимального кодового расстояния произвольного блокового кода С необходимо вычислить 2k(2k-1) расстояний между различными парами кодовых слов. Часто эта задача практически невыполнима. Одним из важных преимуществ линейных блоковых кодов является то, что для вычисления dmin достаточно знать только Хемминговы веса 2k-1 ненулевых слов. Двоичный линейный (n,k)-код С с минимальным расстоянием Хемминга dmin>=2t+1 может обнаружить dmin-1 ошибок и исправить t ошибок. Пример 1. Выполнение типового задания для заданной генерирующей матрицы G. 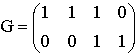 А) Известно, что генерирующая матрица имеет размер (k x n), где k – число строк матрицы, а n – число столбцов. Скорость кода вычисляется как отношение значения k к значению n. Следовательно, длина n кода равна 4, размерность кода k равна 2, а скорость кода равна 2/4=1/2. В) Для вычисления количества кодовых слов воспользуемся тем фактом, что двоичный (n,k)-код С любому двоичному вектору длины k ставит в соответствие одно кодовое слово длины n. Следовательно количество кодовых слов кода С совпадает с числом всех возможных двоичных векторов длины k; число таких векторов определяется как 2k. В рассматриваемом примере число кодовых слов равно 22=4. C) Преобразуем матрицу G в систематический вид . Для чего переставим второй и четвертый столбцы: 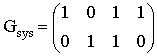 т 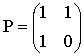 аким образом, проверочная подматрица равна аким образом, проверочная подматрица равна Отметим, что в данном случае выполняется соотношение Р=РТ. Коды, у которых выполняется такое соотношение, называются самодуальными. Согласно формуле запишем п 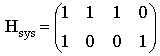 атрицу атрицуD) Информационными словами u являются все возможные двоичные слова длины k=2. Кодовые слова v вычислим, используя формулу v=u*G. Отметим, что в зависимости от того, в систематическом или несистематическом виде использовать порождающую матрицу, одному и тому же информационному слово могут соответствовать различные кодовые слова. Несмотря на это полученные коды будут изоморфными.
E) Организуем таблицу размером 5 столбцов и 4 строки. Выполним шаг А процедуры построения декодирующая таблицы. А именно, запишем в заголовок таблицы все информационные слова, а в первую строку соответствующие им кодовые слова. Для выполнения этих действий воспользуемся результатами, полученными при выполнении задания D. Для j=1 находим произвольное слово e1IV2 минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Пусть e1=1000, вычисляем синдром этого вектора по формуле s=e*HT 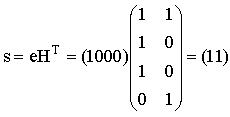 Запишем полученный синдром s1=11 в первый столбец второй строки. В остальных ячейках этой строки запишем суммы кодовых слов из первой строки и вектора ошибок e1=1000. Увеличиваем j на единицу. Для j=2 находим произвольное слово e2IV2 минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Пусть e2=0100, вычисляем синдром этого вектора  Запишем полученный синдром s2=10 в первый столбец третьей строки. В остальных ячейках этой строки запишем суммы кодовых слов из первой строки и вектора ошибок e2=0100. Увеличиваем j на единицу. Для j=3 находим произвольное слово e3IV2 минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Пусть e3=0001, вычисляем синдром этого вектора 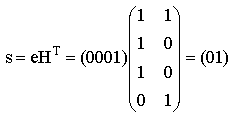 Запишем полученный синдром s3=01 в первый столбец четвертой строки. В остальных ячейках этой строки запишем суммы кодовых слов из первой строки и вектора ошибок e3=0001.
Увеличиваем j и заканчиваем построение таблицы, так как для j=4 не выполняется условие j<2n-k. У рассматриваемого кода 4 смежных класса, лидерами которых являются: e0=0000, e1=1000, e2=0100, e3=0001. При построении таблицы в качестве вектора ошибок не был выбран вектор e=0010. Причина этого заключается в том, что синдром этого вектора совпадает с синдромом вектора e2=0100, что в свою очередь происходит из-за того, что данный код является кодом с неравной защитой от ошибок, то есть число исправляемых ошибок зависит от местоположения ошибок. F) Пусть в канал было передано кодовое слово с=0110, а из канала принято слово r=0010. Рассчитаем синдром для принятого вектора и декодируем его, используя стандартную таблицу. 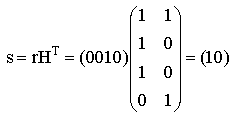 По декодирующей таблице находим, что синдром s=10 находится в третьей строке. В этой же строке отыскиваем вектор r=0010. В первой строке этого же столбца находится переданное кодовое слово с=0110. Одиночная ошибка в слове исправлена. Этот факт выглядит странно, так как минимальное расстояние рассматриваемого кода равно 2, а, следовательно, исправление однократных ошибок не гарантируется. Объяснение этого факта заключается в том, что, как уже отмечалось, данный код является кодом с неравной защитой от ошибок. G) Для вычисления способностей кода по исправлению и обнаружению ошибок вычислим минимальное расстояние Хемминга для этого кода, как минимум Хемминговых весов ненулевых кодовых слов кода С (см. раздел 2.7). Веса Хемминга кодовых слов: wth(0110)=2, wth(1011)=3, wth(1101)=2. Минимальное расстояние Хемминга: dmin=min{2, 3, 2}=2. Используя формулу из раздела 2.8, вычисляем, что рассматриваемый код гарантировано обнаруживает 1 ошибку, а исправляет 0 ошибок. Пример 2. Выполнение типового контрольного задания (см. раздел 1) для заданной проверочной матрицы H. 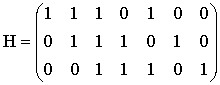 A. Проверочная матрица Н имеет размер (n-k)? n. Следовательно, длина кода n=7, размерность кода k=n-(n-k)=7-3=4, скорость кода равна 4/7. B. Число кодовых слов определяется как 2k=24=16. C. Приведем матрицу H к систематическому виду. П 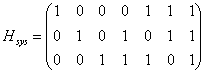 ереставим местами столбцы 2 и 6, 3 и 7. ереставим местами столбцы 2 и 6, 3 и 7. Правые четыре столбца матрицы Hsys представляют собой транспонированную проверочную подматрицу Р. Выпишем матрицу Р: 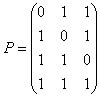 Согласно формуле 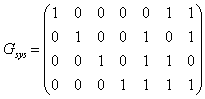 D. Информационными словами u являются все возможные двоичные слова длины k=4. Кодовые слова v вычислим, используя формулу v=u*Hsys и используя матрицу Hsys.
E. Стандартная декодирующая таблица этого кода должна содержать 2n?k=27?4=8 строк и 2k+1=24+1=17 столбцов. Для удобства разделим эту таблицу по ширине на две части (табл. 1), которые заполним согласно процедуре построения из раздела 2.4. У рассматриваемого кода 8 смежных классов, лидерами которых являются: e0=0000000, e1=0000001, e2=0000010, e3=0000100, e4=0001000, e5=0010000, e6=0100000, e7=1000000. F) Пусть в канал было передано кодовое слово с=0011001 (соответствующее информационному слову u=0011), а из канала принято слово r=1011001 (содержащее один ошибочный символ). Синдромом для r является вектор s: 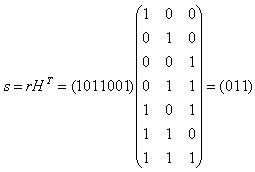 В табл. 1 синдрому s=(011) соответствует строка 5, двигаясь по этой строке, отыскиваем полученный из канала вектор r=1011001 и находим соответствующее этому вектору информационное слово u=0011. Вывод: декодирование успешно. Пусть теперь в канал было передано кодовое слово с=0011001 (соответствующее информационному слову u=0011), а из канала принято слово r=1011011 (два ошибочных символа). Вычислим синдром s: 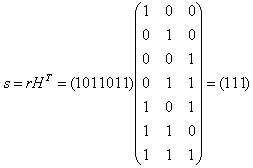 В табл. 1 синдрому s=(111) соответствует строка 2, двигаясь по этой строке, отыскиваем полученный из канала вектор r=1011011 и находим соответствующее этому вектору кодовое слово u=1011. Вывод: декодирование неудачно. G) Минимальное расстояние Хемминга этого кода найдем как минимум Хемминговых весов dmin=min{ wth(0001111)=4, wth(0010110)=3, wth(0011001)=3, wth(0100101)=3, wth(0101010)=3, wth(0110011)=4, wth(0111100)=4, wth(1000011)=3, wth(1001100)=3, wth(1010101)=4, wth(1011010)=4, wth(1100110)=4, wth(1101001)=4, wth(1110000)=3, wth(1111111)=8}=3. Следовательно, рассматриваемый код гарантировано обнаруживает две, а исправляет 1 ошибку. Таблица 1. Часть 1
Таблица 1. Часть 2
|
