Лабораторная 3. Практическая работа по дисциплине Компьютерные технологии в медикобиологической практике

• Название: Практическая работа по дисциплине Компьютерные технологии в медикобиологической практике
• Анкор: Лабораторная 3
• Дата: 18.03.2022
• Размер: 95.13 Kb.
• Имя файла: lab3.docx
• Тип: Практическая работа; #403763

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

ФАКУЛЬТЕТ «ПРИБОРОСТРОЕНИЕ И ТЕХНИЧЕСКОЕ РЕГУЛИРОВАНИЕ»

Кафедра «Приборостроение и биомедицинская инженерия»

Практическая работа

по дисциплине «Компьютерные технологии в медико-биологической практике»

«Основы цифровой фильтрации сигналов»

Выполнил: ст.гр.ПСп42

Коноваленко Р.В.

Проверил:

Бабенко Е. В.


Ростов-на-Дону

2021

Цель лабораторной работы: изучение методики проектирования

цифровых фильтров.

Краткая теория

Фильтрация - это выделение из сигнала его части, спектр которой лежит в определенной области частот. Фильтрация сигнала применяется для выделения полезного сигнала на фоне помех и частотного анализа.

Фильтры характеризуются передаточной характеристикой. Амплитудно- частотная характеристика (АЧХ) характеризует зависимость коэффициента передачи фильтра от частоты. АЧХ может быть представлена в линейном, логарифмическом масштабе. При логарифмическом масштабе уровень АЧХ измеряется в децибелах. Ноль децибелов равен коэффициенту передачи фильтра в 1.

По виду преобразований фильтры делятся на аналоговые и цифровые фильтры.

По зависимости модуля коэффициента передачи от частоты фильтры делятся на фильтры нижних частот (ФНЧ), верхних частот (ФВЧ), полосовые, режекторные, гребенчатые. По виду импульсной характеристики цифровые фильтры делятся на фильтры с бесконечной импульсной характеристикой (БИХ или IIR) и фильтры с бесконечной импульсной характеристикой (КИХ или FIR).

В системе MATLAB для проектирования фильтров и фильтрации сигналов используются следующие основные функции.

1. 
   Примеры.
   
   2. 
      Спроектируем полосовой фильтр 6-го порядка (рис.1).
      

f = [0 0.2 0.2 0.4 0.4 1]; m = [0 0 1 1 0 0];

[b,a] = yulewalk(8,f,m); freqz(b,a,128);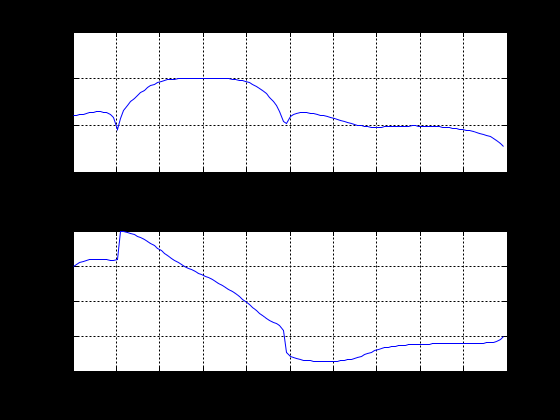



Рисунок 1 - АЧХ и ФЧХ полосового фильтра Юла-Уокера
1.3 Спроектируем режекторный фильтр Баттерворта 6-го порядка с частотами

среза 20 и 50 Гц и построим АЧХ и ФЧХ (рис.2)

fs=256; n=6; Wn=[20/128 50/128];

[b,a] = butter(n, Wn, 'stop');;

N=128; freqz(b,a, N,fs)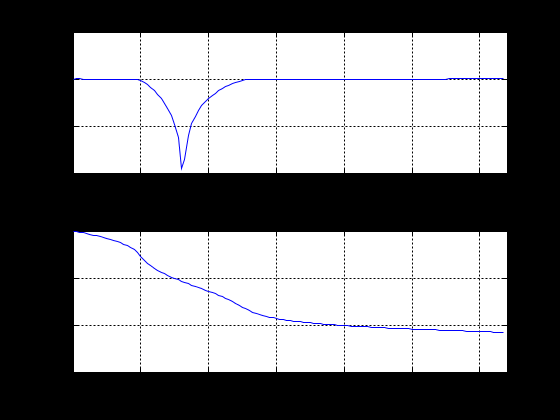



Рисунок 2 - АЧХ и ФЧХ режекторного фильтра Баттерворта
1.3 Спроектируем ФНЧ Чебышева I –го типа 6-го порядка, с частотой среза 40 Гц, допустимой пульсацией 0.1 dB (рис.3)

fs=256; R=0.1; n=6; Wp=40/128;

[b,a] = cheby1(n,R,Wp); N=128; freqz(b,a, N,fs)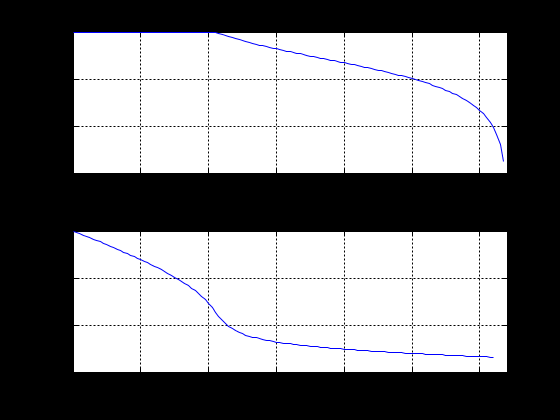



Рисунок 3- АЧХ и ФЧХ ФНЧ Чебышева I-го типа

2. 
   Алгоритм, программа и методические указания
   

Рассмотрим методику проектирования фильтров на следующем примере:

% Спроектируем ФНЧ Юла-Уокера, Баттерворта и Чебышева.

% Фильтры должны удалить синусоиды с частотой 30 и 50 Гц

fp= 0.15; % Относительная частота среза

fy = [0 fp fp 0.6 1]; % Нормированный частотный диапазон.

Hy = [1 1 0 0 0 ]; % Нормированная амплитуда

fs = 250; % Частота дискретизации

fz = fy*fs/2; % Частотный диапазон

N = 6; % Порядок фильтра.

ripple = .1; % Пульсация фильтра Чебышева

% Коэффициенты полиномов цифровых фильтров

[By,Ay] = yulewalk(N,fy,Hy) ;

[Bb,Ab] = butter(N, fp, 'low');

[Bc,Ac] = cheby1(N, ripple, fp, 'low');

% АЧХ цифровых фильтров

n = 126; hy = abs(freqz(By,Ay,n));

hb = abs(freqz(Bb,Ab,n));

hc = abs(freqz(Bc,Ac,n));

h = [hy hb hc]; ff = fs/(2*n) * (0:n-1);

figure(1); subplot(2, 1,1); plot(fz,Hy,ff,h); axis([0 80 0 1.4]);

legend({'Ideal' , 'YuleWalk', 'Butterworth', 'Chebyshev'});

title(' Magnitude Response'); xlabel('Frequency (Hz)');

ylabel('Magnitude'); grid

% АЧХ фильтров в логарифмической шкале.

subplot(2, 1,2); plot(ff(2:n),20*log10(h(2:n,:)))

axis([0 80 -250 50]); grid

title('YuleWalk, Butterworth and Chebyshev filters')

xlabel('Frequency (Hz)'); ylabel('Magnitude in dB'); pause

% Суммарный сигнал

t = (1:500)/fs; s1 = sin(2*pi*t*15); s2=sin(2*pi*t*30); s3=sin(2*pi*t*50);

s = s1+s2+s3;

figure(2); subplot(2, 1,1); plot(t, s);

axis([0 1 -3 3]); title(' Waveform Sin(15+30+50) Hz'); grid

% Фильтрация сигнала

sy = filter(By,Ay, s); sb = filter(Bb,Ab, s);

sc = filter(Bc,Ac, s); sybc=[ sy' sb' sc'];

subplot(2, 1,2); plot(t,sybc); axis([0 1 -3 3]);

title ('Signal after filtering '); xlabel('Time, s. ');

legend({ 'YuleWalk', 'Butterworth', 'Chebyshev'}); grid; pause

% Выполним спектральный анализ сигнала до и после фильтрации.

S =abs(fft(s,512)'); Sy = abs(fft(sy,512)');

Sb = abs(fft(sb,512)'); Sc = abs(fft(sc,512)');

Sf=[S Sy Sb Sc]; w = (0:255)/256*(fs/2);

figure(3); plot(w(2:n),Sf(2:n,:)); grid

title (' Original Signal & after filtering Spectrum ');

xlabel('Frequency (Hz)'); ylabel('Mag. of Fourier transform');

legend({'Original' , 'YuleWalk', 'Butterworth', 'Chebyshev'});
Результаты выполнения программы приведены на рисунках 4-6.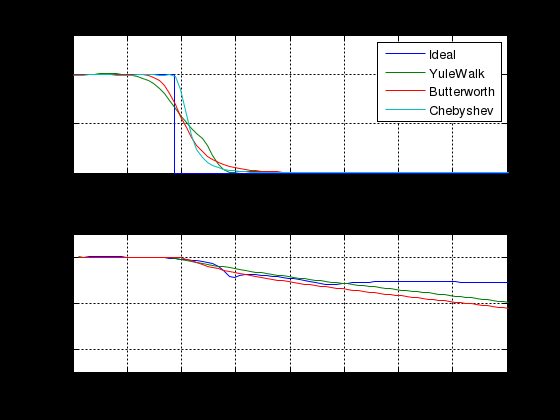



Рисунок 4 - АЧХ цифровых фильтров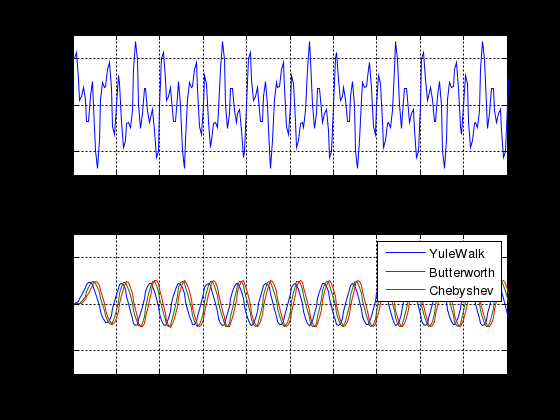


Рисунок 5 - Исходный и отфильтрованный сигналы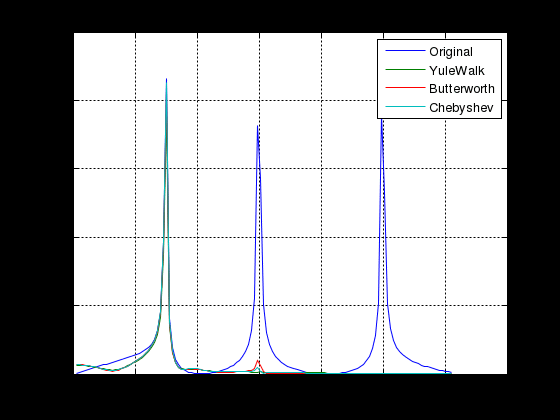



Рисунок 6 - Спектральная мощность исходного сигнала и после фильтрации

3. 
   Задание
   

Спроектируем ФНЧ с исходными сигналами частот: 3, 20, 50 Гц. При проектировании удаляем частоты 20 и 50 Гц, а пропускаем 3 Гц.

Методика проектирования ФНЧ:

% Спроектируем ФНЧ Юла-Уокера, Баттерворта и Чебышева.

% Фильтры должны удалить синусоиды с частотой 20 и 50 Гц

fp= 0.03; % Относительная частота среза

fy = [0 fp fp 0.6 1]; % Нормированный частотный диапазон.

Hy = [1 1 0 0 0 ]; % Нормированная амплитуда

fs = 250; % Частота дискретизации

fz = fy*fs/2; % Частотный диапазон

N = 6; % Порядок фильтра.

ripple = .1; % Пульсация фильтра Чебышева

% Коэффициенты полиномов цифровых фильтров

[By,Ay] = yulewalk(N,fy,Hy) ;

[Bb,Ab] = butter(N, fp, 'low');

[Bc,Ac] = cheby1(N, ripple, fp, 'low');

% АЧХ цифровых фильтров

n = 126; hy = abs(freqz(By,Ay,n));

hb = abs(freqz(Bb,Ab,n));

hc = abs(freqz(Bc,Ac,n));

h = [hy hb hc]; ff = fs/(2*n) * (0:n-1);

figure(1); subplot(2, 1,1); plot(fz,Hy,ff,h); axis([0 80 0 1.4]);

legend({'Ideal' , 'YuleWalk', 'Butterworth', 'Chebyshev'});

title(' Magnitude Response'); xlabel('Frequency (Hz)');

ylabel('Magnitude'); grid

% АЧХ фильтров в логарифмической шкале.

subplot(2, 1,2); plot(ff(2:n),20*log10(h(2:n,:)))

axis([0 80 -250 50]); grid

title('YuleWalk, Butterworth and Chebyshev filters')

xlabel('Frequency (Hz)'); ylabel('Magnitude in dB'); pause

% Суммарный сигнал

t = (1:500)/fs; s1 = sin(2*pi*t*3); s2=sin(2*pi*t*20); s3=sin(2*pi*t*50);

s = s1+s2+s3;

figure(2); subplot(2, 1,1); plot(t, s);

axis([0 1 -3 3]); title(' Waveform Sin(3+20+50) Hz'); grid

% Фильтрация сигнала

sy = filter(By,Ay, s); sb = filter(Bb,Ab, s);

sc = filter(Bc,Ac, s); sybc=[ sy' sb' sc'];

subplot(2, 1,2); plot(t,sybc); axis([0 1 -3 3]);

title ('Signal after filtering '); xlabel('Time, s. ');

legend({ 'YuleWalk', 'Butterworth', 'Chebyshev'}); grid; pause

% Выполним спектральный анализ сигнала до и после фильтрации.

S =abs(fft(s,512)'); Sy = abs(fft(sy,512)');

Sb = abs(fft(sb,512)'); Sc = abs(fft(sc,512)');

Sf=[S Sy Sb Sc]; w = (0:255)/256*(fs/2);

figure(3); plot(w(2:n),Sf(2:n,:)); grid

title (' Original Signal & after filtering Spectrum ');

xlabel('Frequency (Hz)'); ylabel('Mag. of Fourier transform');

legend({'Original' , 'YuleWalk', 'Butterworth', 'Chebyshev'});
Результаты выполнения программы приведены на рисунках 7-9.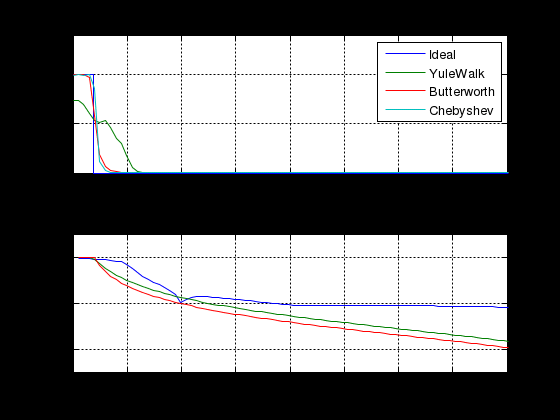



Рисунок 7 - АЧХ цифровых фильтров
На рисунке 7 представлена АЧХ фильтра нижних частот. На графиках визуально заметно, что все частоты до 3 Гц были пропущены, после – были подавлены.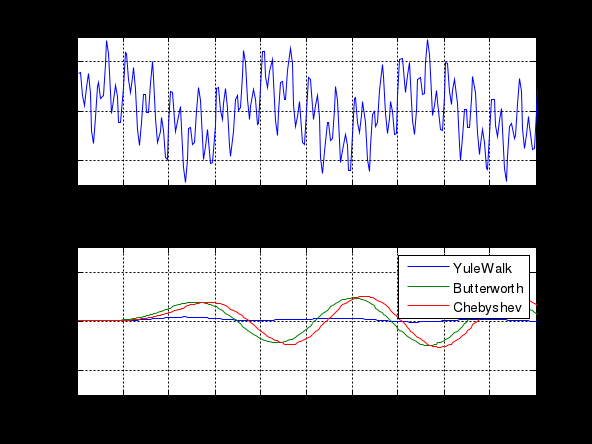



Рисунок 8 - Исходный и отфильтрованный сигналы
Из рисунка 8 видно, что ФНЧ сработал и пропустил одну частоту – 3 Гц. Это показывает форма сигнала после фильтрации.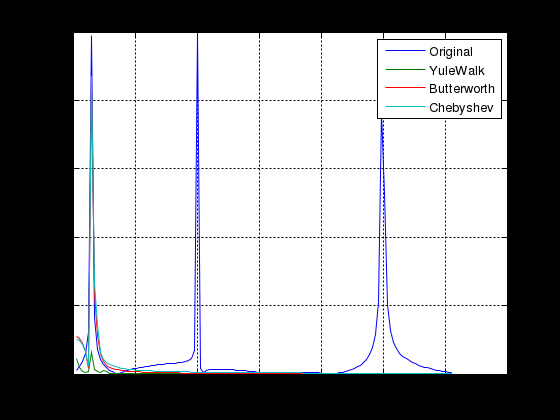



Рисунок 9 - Спектральная мощность исходного сигнала и после фильтрации
На рисунке 9 наблюдается действие фильтра Чебышева, который пропускает только частоту 3 Гц, отмечен на графике бирюзовым цветом. Остальные фильтры показывают, что частоты 20 и 50 Гц не были пропущены.
Спроектируем ФВЧ с исходными сигналами частот: 3, 20, 50 Гц. При проектировании удаляем частоту 3 Гц, а пропускаем 20 и 50 Гц.

Методика проектирования ФВЧ:

% Спроектируем ФВЧ Юла-Уокера, Баттерворта и Чебышева.

% Фильтры должны удалить синусоиды с частотой 20 и 50 Гц

fp= 0.03; % Относительная частота среза

fy = [0 fp fp 0.6 1]; % Нормированный частотный диапазон.

Hy = [0 0 1 1 1 ]; % Нормированная амплитуда

fs = 250; % Частота дискретизации

fz = fy*fs/2; % Частотный диапазон

N = 6; % Порядок фильтра.

ripple = .1; % Пульсация фильтра Чебышева

% Коэффициенты полиномов цифровых фильтров

[By,Ay] = yulewalk(N,fy,Hy) ;

[Bb,Ab] = butter(N, fp, 'high');

[Bc,Ac] = cheby1(N, ripple, fp, 'high');

% АЧХ цифровых фильтров

n = 126; hy = abs(freqz(By,Ay,n));

hb = abs(freqz(Bb,Ab,n));

hc = abs(freqz(Bc,Ac,n));

h = [hy hb hc]; ff = fs/(2*n) * (0:n-1);

figure(1); subplot(2, 1,1); plot(fz,Hy,ff,h); axis([0 80 0 1.4]);

legend({'Ideal' , 'YuleWalk', 'Butterworth', 'Chebyshev'});

title(' Magnitude Response'); xlabel('Frequency (Hz)');

ylabel('Magnitude'); grid

% АЧХ фильтров в логарифмической шкале.

subplot(2, 1,2); plot(ff(2:n),20*log10(h(2:n,:)))

axis([0 80 -250 50]); grid

title('YuleWalk, Butterworth and Chebyshev filters')

xlabel('Frequency (Hz)'); ylabel('Magnitude in dB'); pause

% Суммарный сигнал

t = (1:500)/fs; s1 = sin(2*pi*t*3); s2=sin(2*pi*t*20); s3=sin(2*pi*t*50);

s = s1+s2+s3;

figure(2); subplot(2, 1,1); plot(t, s);

axis([0 1 -3 3]); title(' Waveform Sin(3+20+50) Hz'); grid

% Фильтрация сигнала

sy = filter(By,Ay, s); sb = filter(Bb,Ab, s);

sc = filter(Bc,Ac, s); sybc=[ sy' sb' sc'];

subplot(2, 1,2); plot(t,sybc); axis([0 1 -3 3]);

title ('Signal after filtering '); xlabel('Time, s. ');

legend({ 'YuleWalk', 'Butterworth', 'Chebyshev'}); grid; pause

% Выполним спектральный анализ сигнала до и после фильтрации.

S =abs(fft(s,512)'); Sy = abs(fft(sy,512)');

Sb = abs(fft(sb,512)'); Sc = abs(fft(sc,512)');

Sf=[S Sy Sb Sc]; w = (0:255)/256*(fs/2);

figure(3); plot(w(2:n),Sf(2:n,:)); grid

title (' Original Signal & after filtering Spectrum ');

xlabel('Frequency (Hz)'); ylabel('Mag. of Fourier transform');

legend({'Original' , 'YuleWalk', 'Butterworth', 'Chebyshev'});

Результаты выполнения программы приведены на рисунках 10-12.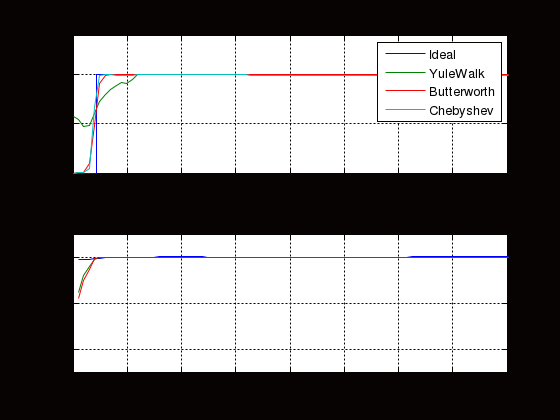



Рисунок 10 - АЧХ цифровых фильтров
На рисунке 10 представлена АЧХ фильтра верхних частот. На графиках визуально заметно, что все частоты после 3 Гц были пропущены, а до – были подавлены.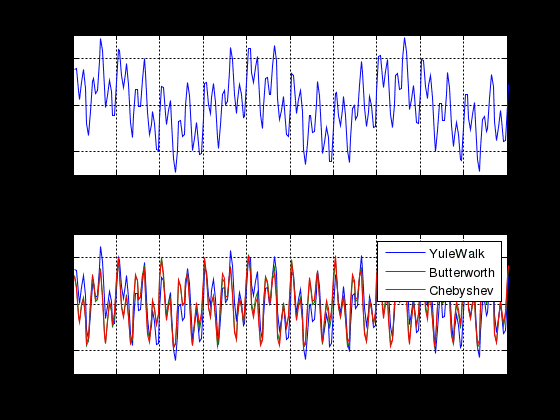


Рисунок 11 - Исходный и отфильтрованный сигналы
Из рисунка11 видно, что ФВЧ сработал и пропустил две частоты – 20 и 50 Гц. Это показывает форма сигнала после фильтрации.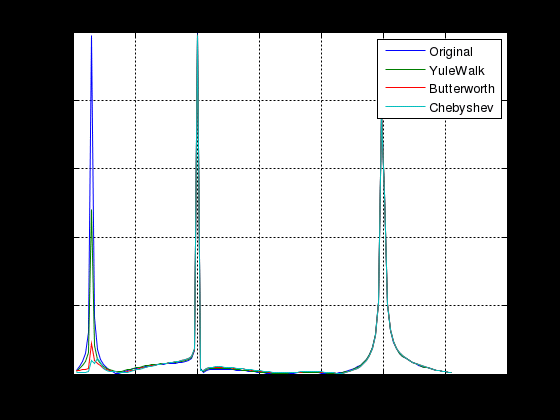



Рисунок 12 - Спектральная мощность исходного сигнала и после фильтрации
На рисунке 12 наблюдается действие фильтра Чебышева, который пропускает две частоты 20 и 50 Гц, отмечены на графике бирюзовым цветом. Остальные фильтры показывают, что частота 3 Гц не была пропущена.
Вывод: в результате лабораторной работы мы изучили методику проектирования цифровых фильтров. Приобрели следующие компетенции: знание основ проектирования цифровых фильтров, функции системы Matlab, применяемые для проектирования фильтров, алгоритм цифровой фильтрации, графическое отображение результатов, анализ полученных данных.

При пропускании нижних частот, фильтр пропустил нижние. При пропускании верхних частот – верхние.