Практическая работа по теме Решения систем уравнений методом Гаусса
 Скачать 33.56 Kb. Скачать 33.56 Kb.
|
|
Практическая работа по теме «Решения систем уравнений методом Гаусса» Цели работы: расширить представление о методах решения СЛУ и отработать алгоритм решения СЛУ методом Гаусса; развивать логическое мышление студентов, умение находить рациональное решение задачи; воспитывать у студентов культуру письменной математической речи при оформлении ими своего решения. Основной теоретический материал. М 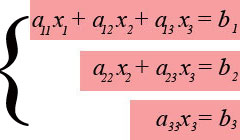 етод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной. Пример такой системы - на рисунке сверху. етод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной. Пример такой системы - на рисунке сверху. Решите систему линейных уравнений методом Гаусса. Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент 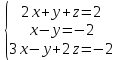 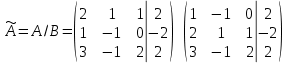 Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей - три первых: 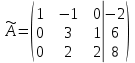 Все элементы третьей строки делим на два 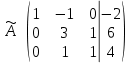 Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1: 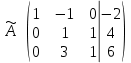 От третьей строки отнимаем вторую, умноженную на 3: От третьей строки отнимаем вторую, умноженную на 3: 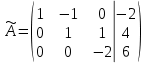 Умножив третью строку на 0,5 , получаем: Умножив третью строку на 0,5 , получаем: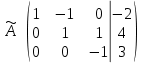 Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент 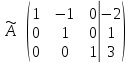 Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:  Полученной матрице соответствует система 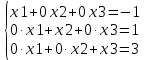 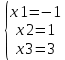 Ответ. Ответ. 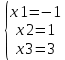 Задания для самостоятельного решения: ВАРИАНТ 1 Решите системы линейных уравнений методом Гаусса: 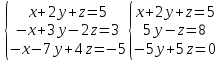 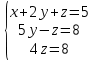 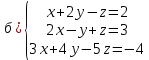 . в) . в)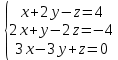 ВАРИАНТ 2 Решите системы линейных уравнений методом Гаусса: а) 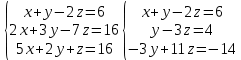 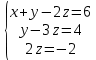 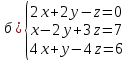 в) в)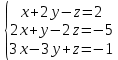 Критерии оценивания: Работа оценивается на «3»,если: записано решение примера и выполнена проверка решения системы; самостоятельно методом Гаусса верно решена одна из систем. Работа оценивается на «4»,если: самостоятельно методом Гаусса верно решены любые две системы. Работа оценивается на «5»,если: самостоятельно методом Гаусса верно решены три системы. |
