2 СД 3 9 кл_3 ЕБА. Практическая работа по теме Статистическая обработка результатов медикобиологического исследования с помощью ms excel
 Скачать 172.73 Kb. Скачать 172.73 Kb.
|
|
Практическая работа по теме: «Статистическая обработка результатов медико-биологического исследования с помощью MS Excel» Дискретные вариационные ряды в MS Excel ФИО преподавателя: Пышкина Т.В. Электронная почта: t_pyshkina@inbox.ru Теоретическая часть. Вариационный ряд - это статистический ряд, показывающий распределение изучаемого явления по величине какого-либо количественного признака. Например, больных по возрасту, по срокам лечения, новорожденных по весу и т.п. Варианта - отдельные значения признака, по которому проводится группировка. Частота - число, показывающее, как часто встречается та или иная варианта. Сумма всех частот показывает общее число наблюдений. Разность между наибольшей и наименьшей вариантой вариационного ряда называется размахом или амплитудой. РАЗЛИЧАЮТ ВАРИАЦИОННЫЕ РЯДЫ: 1. Прерывные (дискретные) и непрерывные. Ряд считается непрерывным, если группировочный признак может выражаться дробными величинами (вес, рост т.п.), прерывным, если группировочный признак выражается только целым числом (дни нетрудоспособности, число ударов пульса и т.п.). 2.Простые и взвешенные. Простой вариационный ряд представляет собой ряд, в котором количественное значение варьирующего признака встречается один раз. Во взвешенном вариационном ряду количественные значения варьирующего признака повторяются с определённой частотой. 3. Сгруппированные (интервальные) и несгруппированые. Сгруппированный ряд имеет варианты, объединённые в группы, объединяющие их по величине в пределах определённого интервала. В несгруппированном ряду каждой отдельной варианте соответствует определённая частота. 4. Четные и нечетные. В чётных вариационных рядах сумма частот или общее число наблюдений выражено чётным числом, в нечётных ― нечётным. 5. Симметричные и асимметричные. В симметричном вариационном ряду все виды средних величин совпадают или очень близки (мода, медиана, среднее арифметическое). ГИСТОГРАММА. ПОЛИГОН. Для графического изображения статистического распределения строят полигоны или гистограммы. Гистограммой называется график, по оси абсцисс которого отложены границы интервалов, а по оси ординат – их частоты. Полигон частот можно получить из гистограммы путем соединения срединных значений интервалов. Построение полигонов и гистограмм позволяет произвести первичный анализ экспериментальных данных, а именно: по форме гистограммы сделать предположение о законе распределения случайной величины; выявить наиболее часто встречающиеся значения исследуемой величины и разброс или отклонение относительно этого значения. СТАТИСТИЧЕСКИЕ ФУНКЦИИ MICROSOFT EXCEL МАКС(аргумент1; аргумент2;…) - ищет максимальный из аргументов; МИН(аргумент1; аргумент2;…) - ищет минимальный из аргументов; СРЗНАЧ(аргумент1; аргумент2;…) - вычисляет среднее своих аргументов; СЧЕТ(аргумент1; аргумент2;…) – подсчитывает количество ячеек в диапазоне, который содержит числа. СЧЕТЕСЛИ(диапазон; условие) - подсчитывает число аргументов в диапазоне, отвечающих условию. МЕДИАНА(число1; число2;…) – возвращает медиану исходных чисел. МОДА.ОДН(число1; число2;…) – возвращает значение моды для массива или диапазона значений. СРОТКЛ(число1; число2;…) - возвращает среднее абсолютных значений отклонений точек данных от среднего. ДИСП.В(число1; число2;…) – оценивает дисперсию по выборке. СТАНДОТКЛОН.В(число1; число2;…) - оценивает стандартное отклонение по выборке. Практическая часть. Цель: Познакомиться с возможностью использования математических и статистических функций табличного процессора MS Excel для расчета статистических характеристик во временной области. Содержание работы. ЗАДАНИЕ 1. Пусть обследована группа пациентов, у которых был измерен уровень цинка в сыворотке крови в физиологических условиях. Результаты измерений были сгруппированы в вариационный ряд. Было установлено, что у 2 человек уровень цинка находится в интервале от 75 до 84 мкг%, у 5 - в интервале от 85 до 94 мкг% и т.д. Середина каждого интервала вариационного ряда, образованного такой группировкой, называется вариантой x, а количество человек, уровень цинка которых лежит в одном и том же интервале - частотой f. Параметр f характеризует, как часто встречается в ходе исследований тот или иной результат. Результаты измерений сведены в таблицу 1: Таблица 1. Уровень цинка в сыворотке крови в физиологических условиях 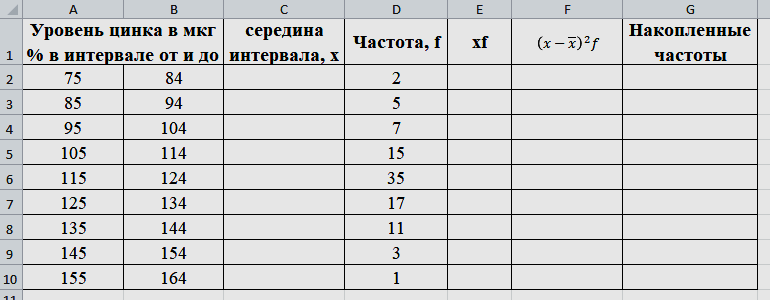 В документе MS Excel Вариационный ряд1.xlsx на листе «Уровень цинка» выполните следующие задания: Создайте данную таблицу в MS Excel и заполните пустые клетки таблицы, вставив необходимые расчетные формулы. Определите характеристики вариационного ряда по данным, приведенным в таблице 1. Оформите результаты расчетов в виде таблицы 2: Таблица 2. Результаты обработки данных вариационного ряда  Где: а) n - общее число наблюдений (количество обследованных пациентов) 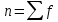 . .б) 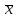 - взвешенное среднее арифметическое (среднее значение уровня цинка) - взвешенное среднее арифметическое (среднее значение уровня цинка) 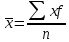 . .в) Мода вариационного ряда (наиболее часто встречаемый уровень цинка, величина находится в интервале с максимальным значением частоты f) 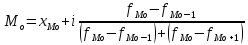 г) Медиана вариационного ряда (середина ряда, грубо может быть определена как половина суммы минимального и максимального уровней цинка) 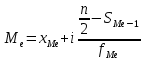 , где , гдеxMe, xMo- начальное значение интервала, содержащего медиану и моду соответственно i - ширина интервала SMe-1 - накопленная частота до интервала, содержащего медиану fMe - частота вариант в интервале, содержащем медиану fMо, fMо-1, fMо+1 - частота вариант в интервале, содержащем моду, и частоты вариант в соседних интервалах д) Среднеквадратическое отклонение (характеризует среднее значение разброса значений уровня цинка у разных пациентов относительно среднего значения) 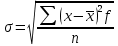 Постройте полигон вариационного ряда - зависимость f(x). По виду данного графика можно оцените степень случайности исследуемого параметра. ХОД РАБОТЫ: Откройте новый документ MS Excel/ Переименуйте Лист1 в «Уровень цинка». На листе «Уровень цинка» в ячейках A1:G10 создайте таблицу 1, как в образце. На листе «Уровень цинка» в ячейках A12:E13 создайте таблицу 2, как в образце. Найдите середину каждого интервала. Для этого в ячейке C2 введите формулу: =(A2+B2)/2. Методом автозаполнения скопируйте формулу из ячейки C2 в ячейки C3:C10. В ячейках E2:E10 найдите произведение xf, т.е. перемножьте ячейки столбцов C и D. В ячейке A13 найдите общее число наблюдений. Для этого введите формулу: =СУММ(D2:D10). В ячейке B13 найдите среднее арифметическое. Для этого введите формулу: =СУММ(E2:E10)/A13. Найдите произведение 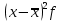 . Для этого в ячейке F2 введите формулу: =(C2-B$13)^2*D2. Методом автозаполнения скопируйте формулу в ячейки F3:F10. . Для этого в ячейке F2 введите формулу: =(C2-B$13)^2*D2. Методом автозаполнения скопируйте формулу в ячейки F3:F10.Найдите накопленные частоты. Накопленная частота образуется путем суммирования текущей частоты вариационного ряда со всеми предыдущими частотами. Поэтому в ячейке G2 введите формулу: =D2. В ячейке G3 введите формулу: =D3+G2. Методом автозаполнения скопируйте формулу из ячейки G3 в ячейки G4:G10. Найдите моду. Для этого: Определите модальный интервал, т.е. интервал, у которого наибольшая частота. По таблице 1 это интервал 115-124. Значит, в ячейке A6 записана нижняя граница интервала, содержащего моду. В ячейке B6 записана верхняя граница интервала, содержащего моду. В ячейках D6, D5, D7 записаны частота вариант в интервале, содержащем моду, и частоты вариант в соседних интервалах. В ячейке C13 введите формулу: =A6+(B6-A6)*(D6-D5)/((D6-D5)+(D6-D7)). Найдите медиану. Для этого: Определите в ячейке D14 середину ряда как половина суммы минимального и максимального уровней цинка. В ячейке D14 введите формулу: =(B10+A2)/2. Определите медианный интервал, т.е. интервал на который приходится середина ряда, при необходимости числовое значение середины ряда можно предварительно округлить. По таблице 1 это интервал 115-124. Значит, в ячейке A6 записана нижняя граница интервала, содержащего медиану. В ячейке B6 записана верхняя граница интервала, содержащего медиану. В ячейке D6 записана частота вариант в интервале, содержащем медиану. В ячейке G5 записана накопленная частота до интервала, содержащего медиану. В ячейке D13 введите формулу: =A6+(B6-A6)*(A13/2-G5)/D6. Найдите среднеквадратическое отклонение. Для этого в ячейке E13 введите формулу: =КОРЕНЬ(СУММ(F2:F10)/A13). Постройте полигон вариационного ряда - зависимость f(x). Для этого: Выделите ячейки, где записаны частоты f – D2:D10. Выполните команду меню Вставка – График – График. На листе появится график. Введите в качестве числовых обозначений делений горизонтальной оси - середины интервалов. Для этого выполните команду меню Работа с диаграммами – Конструктор – Выбрать данные. В появившемся диалоговом окне в поле Подписи горизонтальной оси нажмите кнопку Изменить и выделите ячейки, в которых записаны середины интервалов, т.е. это ячейки C2:C10. Нажмите OK. Задайте название диаграммы «Полигон вариационного ряда». Для этого выполните команду меню Работа с диаграммами – Макет – Название диаграммы и выберите команду Над диаграммой. В появившемся текстовом поле запишите название. Сохраните файл под именем Вариационный ряд1.xlsx. ЗАДАНИЕ 2. Пусть обследована группа пациентов и получены результаты о длительности пребывания пациентов на терапевтических койках. Результаты измерений были сгруппированы в вариационный ряд. Результаты измерений сведены в таблицу 3: 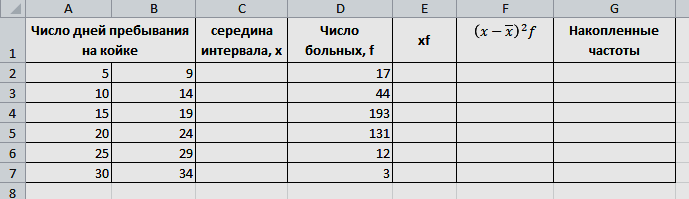 В документе MS Excel Вариационный ряд1.xlsx на листе «Стационар» выполните следующие задания: Создайте данную таблицу в MS Excel и заполните пустые клетки таблицы, вставив необходимые расчетные формулы. Определите характеристики вариационного ряда по данным, приведенным в таблице 3. Оформите результаты расчетов в виде таблицы 4: Таблица 4. Результаты обработки данных вариационного ряда  Постройте полигон вариационного ряда - зависимость f(x). ЗАДАНИЕ 3. Отправьте документ MS Excel Вариационный ряд1.xlsx. преподавателю по электронному адресу t_pyshkina@inbox.ru. |
