Практическое занятие 2 Цель занятия
 Скачать 138.9 Kb. Скачать 138.9 Kb.
|
|
Практическое занятие 2 Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; закрепление навыков решения простейших статистических задач; закрепление навыков применять правила приближенных вычислений; закрепление навыков работы с основными свойствами геометрических фигур на плоскости и в пространстве. Задание 7 (максимальное количество баллов – 3 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6см и 8см, а боковое ребро призмы равно 12см. 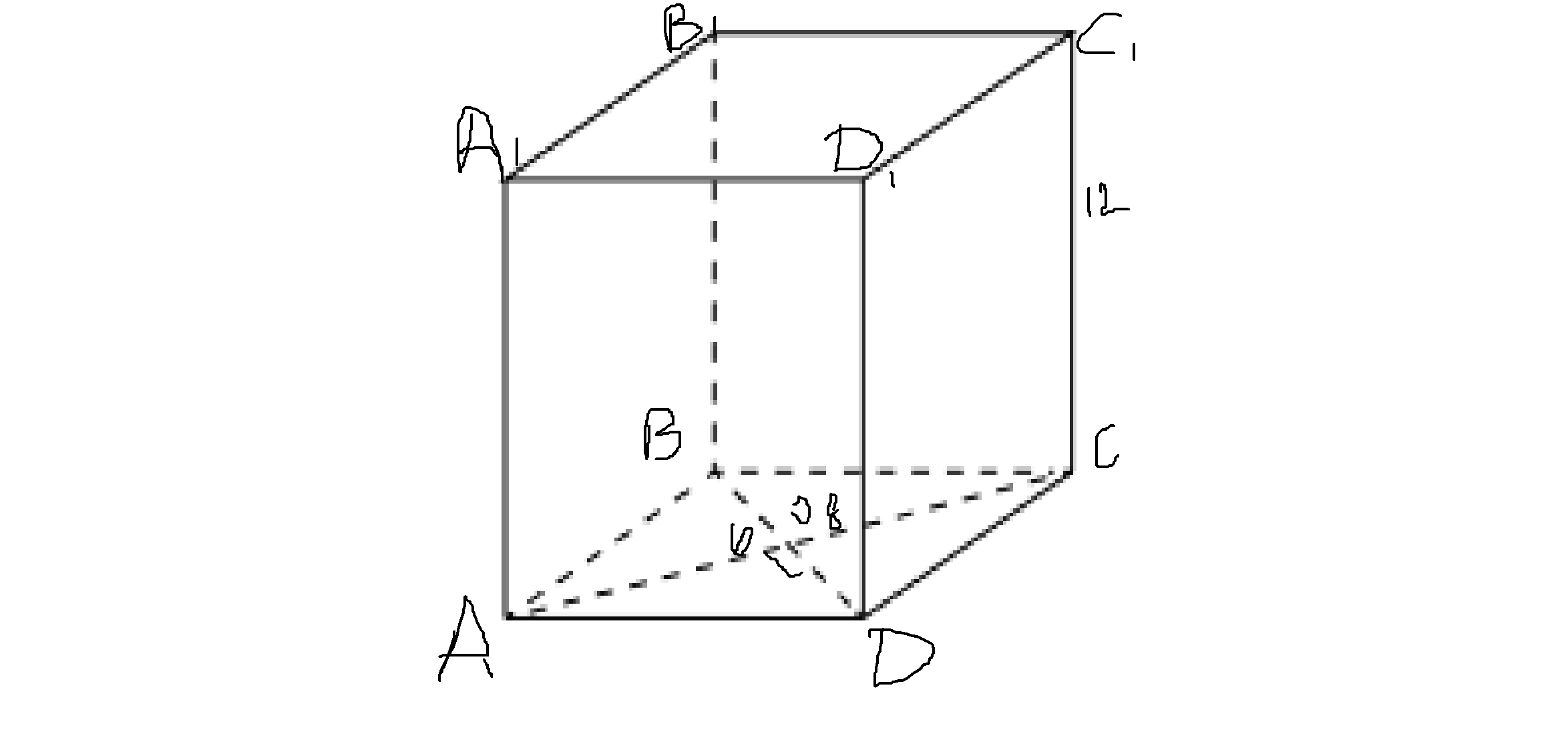 Прямая призма - это призма, боковые ребра которой перпендикулярны основанию. Ее высота равна боковому ребру. Дано: BD= 6 AC=8 CC1=12 Решение: Найдем Sромба с помощью формулы: Sp= 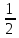 *AC*BD *AC*BD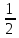 *8*6=24 *8*6=24AO= 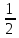 AC= AC= 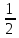 *8=4 *8=4OD= 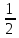 BD= BD=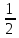 *6=3 *6=3Сторона ромба a выражается через его диагонали d1 и d2 формулой a= 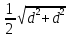 = AD= = AD=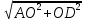 = =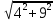 = =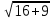 = =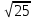 =5 =5Тогда S поверхности призмы равна S=2Sосн+Sбок=2Sp+4*a*H= 48+4*5*12=288 Ответ: Sпрям.призм. 288. Задание 6 (максимальное количество баллов – 4 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 1500. 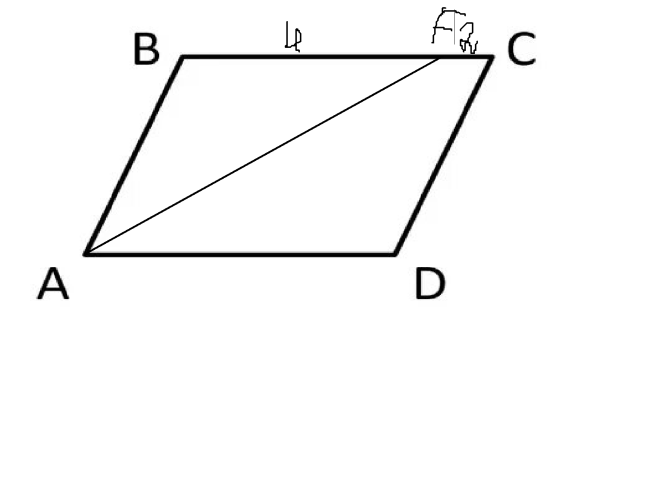 Дано: BF-4 CF-2 ∟ABC= 150⁰ Решение: Накрест лежащие углы равны => BFA=FAD AF- биссектриса ∟BAD, следовательно ∟BFA=∟FAD=∟BAF, треугольник BFA равнобедренный и AB=BF=4, по формуле Sпаралел.= находим SABCD=AB*BC*sin∟ABC=4*6* 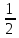 = 24* = 24*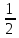 = = 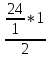 => (сокращаем ) => (сокращаем ) 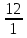 * *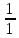 = = 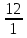 = 12 = 12 Ответ:Sпаралел. 12. Задание 5 (максимальное количество баллов – 3 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см2. Найдите площадь треугольника ABD. 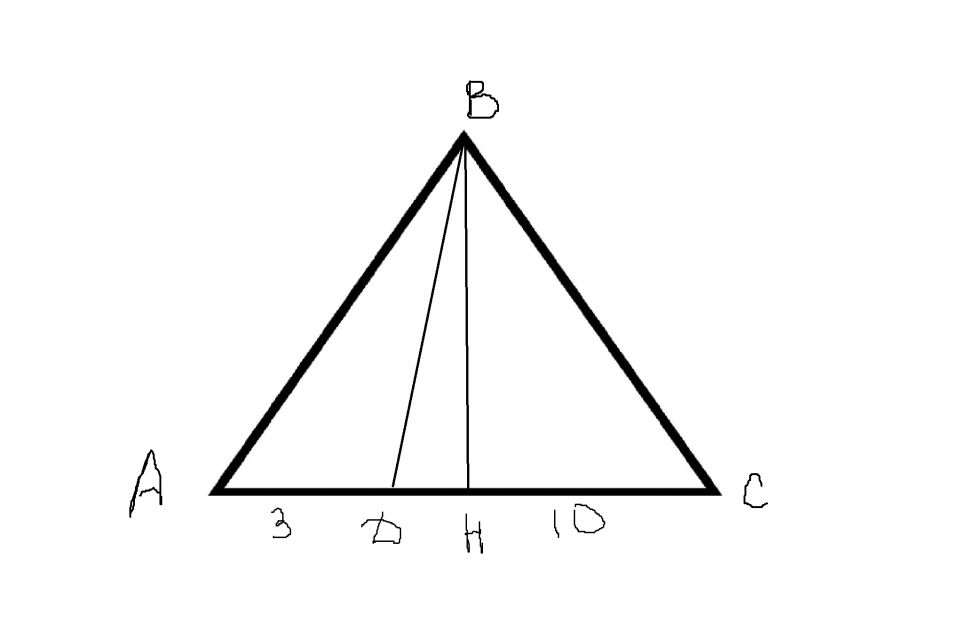 Дано: AD- 3 см DC- 10 см SABC- 39 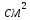 Найти: SABD Решение: Проведем высоту из вершины В на основании АС. ВН является высотой как треугольника АВС , так и ABD. Выразим площади этих треугольников : SADC= 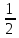 BH*AC BH*ACSABD= 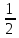 BH*AD BH*ADСоотношение S: 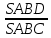 = = 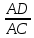 = =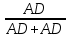 = = 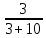 = =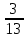 Тогда SABD: SABD =SABC* 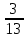 = = 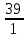 * *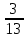 = 9 = 9Ответ : Sтреугол. 9 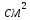 . .Задание 1. (Максимальное количество баллов – 3 балла) Таблица – «Виды моделирования при решении текстовых задач» В таблице «Виды моделирования при решении текстовых задач» заполните позицию «Необходимо определить» в графе «Интерпретация модели».
Задание 4 (максимальное количество баллов - 4 балла) Решите примеры, связанные с погрешностями, подробно описывая ход решения. a) Округлить число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа. b) Число 12,75 определено с относительной погрешностью 0,3, %. Найдите абсолютную погрешность округления. c) Определите верные и сомнительные цифры числа 13,27 ± 0,03. а ) 4.4557|5|2|5|0 4.455753 (тут 3 потому что знак после которого отделяет 5, есл 5 более округляем до след.числа) 4.45575 4.4558 4.456 4.46 4.5 4 б) 12,75 e = 0,3=0,03 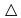 -? -?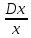 = =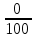 = =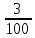 =0,03 =0,03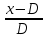 =0,03 =0,03 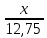 =0,03 =0,0312,75*0,03= 0,3825- абсолютная погрешность в) 13,27 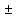 0,03 0,0313,27-0,03= 13,24 13,27+0,03=13,3 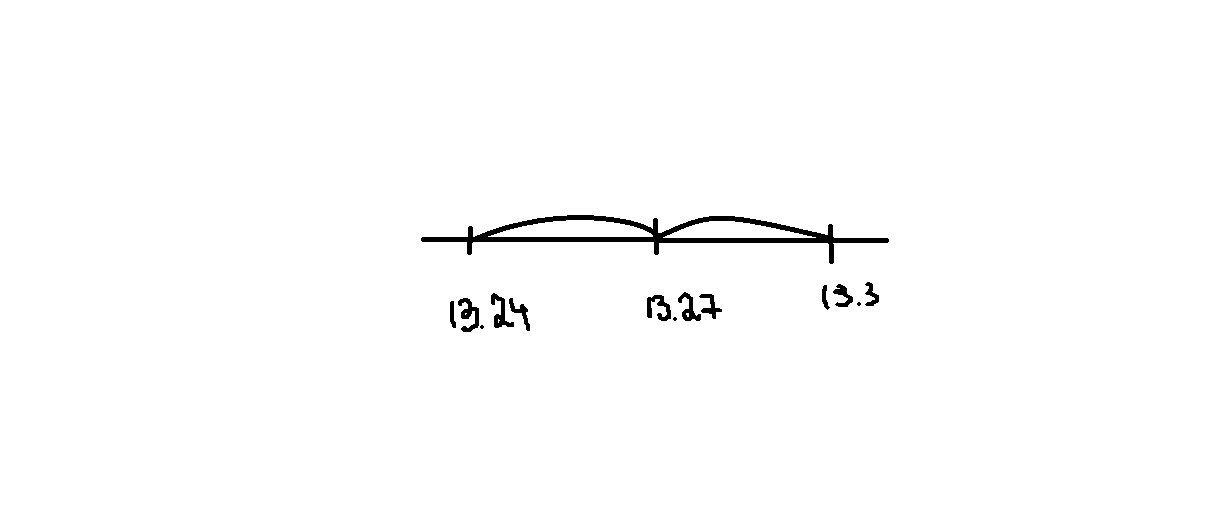 13,24- сомнительное 13,27- верное число 13,3- сомнительное |
