ДЛЯбакалавров13. Практикум по финансовому менеджменту ижевск, 2013 г. Содержание
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
Задачи к теме 5.Финансовые риски и их оценка1. Имеется следующая оценка совместного вероятностного распределения доходностей от инвестиций в акции компаний А и Б:
Вычислите ковариацию и коэффициент корреляции двух инвестиций. Определим среднюю доходность акций: 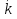 = = 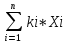 Для акции А: 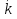 = -10*0,15+ 5*0,2 + 10*0,3+20*0,35 = 9,5% = -10*0,15+ 5*0,2 + 10*0,3+20*0,35 = 9,5%Для акции Б: 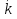 = 15*0,15+10*0,2+5*0,3 = 5,75% = 15*0,15+10*0,2+5*0,3 = 5,75%Определим дисперсию: σ² = 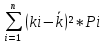 Для акции А: σ² = (-10-9,5)²*0,15 + (5-9,5)²*0,2 + (10-9,5)²*0,3 + (20-9,5)²*0,35 = 99,75% Для акции Б: σ² = (15-5,75)²*0,15 + (10-5,75)²*0,2 + (5-5,75)²*0,3 + (0-5,75)²*0,35 = 28,19% Определим стандартное отклонение: σ = 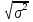 Для акции А: σ = 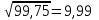 Для акции Б: σ = 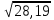 = 5,31 % = 5,31 %Рассчитаем ковариацию: COV= 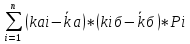 COV=(-10-9,5)*(15-5,75)*0,15 + (5-9,5)*(10-5,75)*0,2 + (10-9,5)*(5-5,75)*0,3 + (20-9,5)*(0-5,75)*0,35 = -52,125% Определим значение коэффициента корреляции: r = 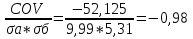 Доходности двух инвестиций движутся в противоположных направлениях. 2. Ожидаемая доходность акций А и Б равна соответственно 12 и 25 %. Их среднеквадратическое отклонение равно 5 и 8%. Коэффициент корреляции между доходностями акций равен 0,6. Рассчитайте ожидаемую доходность и стандартное отклонение портфеля, состоящего на 40% из акций А и на 60% из акций Б. Определите ожидаемую доходность и стандартное отклонение портфеля, состоящего на 60% из акций А и на 40% из акций Б. Сравните полученные результаты. Определим ожидаемую доходность портфеля, если 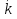 а = 12%, а = 12%, 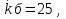 Ха = 0,4, Хб = 0,6: Ха = 0,4, Хб = 0,6: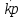 = = 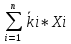 = 12*0,4 + 25*0,6 = 19,8% = 12*0,4 + 25*0,6 = 19,8%Рассчитаем стандартное отклонение портфеля, если σа = 5%, σб = 8%, rаб = 0,6: σp = 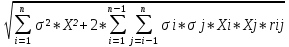 = = 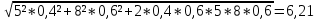 Определим те же показатели, но при другой структуре портфеля: Ха=0,6, Хб = 0,4 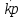 = 12*0,6 + 25*0,4= 17,2% = 12*0,6 + 25*0,4= 17,2%σp = 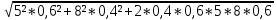 = 5,55% = 5,55%Первый портфель имеет более высокие показатели доходности и риска. 3. Инвестор владеет тремя видами акций. Он произвел оценку следующего совместного вероятностного распределения доходностей:
Определите ожидаемую доходность и стандартное отклонение портфеля, если инвестор вкладывает 30% средств в акции А, 50% - в акции В, 20% - в акции С. Предполагается, то доходность каждой ценной бумаги является некоррелированной с доходностью остальных ценных бумаг. Для решения задачи необходимо определить а) среднюю доходность по акциям А,В,С, б) дисперсию для этих бумаг, в) доходность и стандартное отклонение портфеля. Определим среднюю доходность акций: Для акции А: Для акции В: Для акции С: Определим дисперсию: σ² = 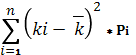 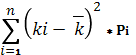 Для акции А: σ² = (-10-4)²*0,3 + (0-4)²*0,2 + (10-4)²*0,3 + (20-4)²*0,2 = 124% Для акции В: σ² = (10-4,4)²*0,3 + (8-4,4)²*0,2 + (6-4,4)²*0,3 + (-10-4,4)²*0,2 = 52,37% Для акции С: σ² = (0-8,6)*0,3 + (10-8,6)*0,2 + (12-8,6)*0,3 + (15-8,6)*0,2 = 34,24% Рассчитаем ожидаемую доходность портфеля при условии, что Xа = 0,3, Xв = 0,5, Xс = 0,2: Рассчитаем стандартное отклонение портфеля: σp = 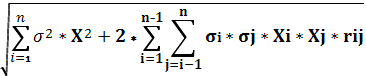 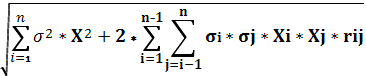 Поскольку rij = 0, то σp = Следовательно, ожидаемая доходность портфеля составит 5,12%, а его стандартное отклонение 5,06%. 4.Портфель инвестора состоит из ценных бумаг со следующими характеристиками:
Доходность безрисковых ценных бумаг равна 5%, доходность на рынке в среднем 10%. Определите бета портфеля, доходность портфеля. Определим долю каждого актива в портфеле: Ха = 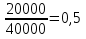 Хб= 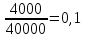 Хс= 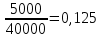 Хд = 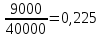 Хе = 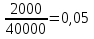 Рассчитаем βр: βр = 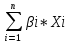 = 0,05*0,5+0,9*0,1+1,1*0,125+1,2*0,225+1,8*0,05 = 0,59 = 0,05*0,5+0,9*0,1+1,1*0,125+1,2*0,225+1,8*0,05 = 0,59Рассчитаем ожидаемую доходность портфеля 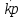 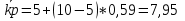 Бета- коэффициент портфеля составит 0,59, а его ожидаемая доходность – 7,95%. 5. Пусть в портфель входят две ценные бумаги со следующими характеристиками:
При условии, что коэффициент корреляции этих ценных бумаг составляет 0,30, а безрисковая ставка равна 5%, определите уравнение рыночной линии. Определим стандартное отклонение портфеля, если Ха = 0,4, Хб = 0,6, σа = 20%, σб = 28%, r = 0,3: 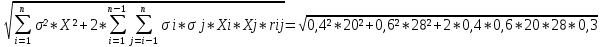 = 19,87% = 19,87%Рассчитаем среднюю доходность рыночного портфеля: 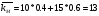 % %Определим уравнение рыночной линии: 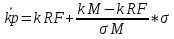 P P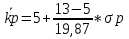 6. Компании А и Б планируют вложить денежные средства в ценные бумаги. При этом у А собственные средства составляют 70 млн.руб., а сумма возможного убытка в случае неправильного выбора объекта инвестирования может составить 1,2 млн.руб., у компании Б- 92 млн.руб., и 8 млн. руб. соответственно. Определите, какое из предприятий осуществляет менее рискованное вложение средств. Для расчета воспользуемся коэффициентом риска: Kp= 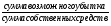 Коэффициент риска для компании А: Kp= 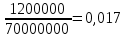 Коэффициент риска для компании Б: Kp= 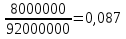 Поскольку коэффициент риска у компании Б выше, то можно сделать вывод о более рискованном вложении средств со стороны этой компании. 7. По модели САРМ определите ожидаемую доходность акции, если: - безрисковая ставка доходности составляет 8% годовых, - среднерыночная ставка доходности финансовых активов – 15%, - бета - коэффициент составляет 2.5. Воспользуемся уравнением рыночной линии ценной бумаги: ki = k RF+ (kM - k RF)*βi = 8+(15-8)*2,5 = 25,5% |
