ТАУ. Практикум по курсу "Основы теории управления" Вариант 22 Хахалев А. Д. Ст гр. 6894

• Название: Практикум по курсу "Основы теории управления" Вариант 22 Хахалев А. Д. Ст гр. 6894
• Дата: 08.06.2022
• Размер: 421 Kb.
• Имя файла: 6257579.doc
• Тип: Практикум; #576629
• страница: 2 из 4

B_e(s) = 1, (1.14)

A(s) = 1 + B_P(s)/A_P(s). (1.15)

Записать через численные значения параметров звеньев ПФ Ф_e(s).

Ф_e(s)= (0.2s² + 1.2s + 1)/ (0.2s² + 1.2s + 41) (1.16)

Результат автоматизированного расчета:

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 1 | 41 | 0 |

| | 1.2 | 1.2 | 1 |

| | 0.2 | 0.2 | 2 |
Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
1.9. Указать выражение, определяющее характеристический полином замкнутой системы через полиномы ПФ разомкнутой системы (получено в п. 1.8):

Для одноконтурной СУ с единичной отрицательной обратной связью характеристи-ческий полином определяется выражением

Вывод о совпадении (или различии) результатов расчета характеристического полинома замкнутой системы при использовании разных ПФ – по управлению и по ошибке:
Расчёты различаются.
1.10. На вход исследуемой системы подается единичное ступенчатое воздействие f(t)=1(t) (изображение этой функции F(s) = 1/s).

Чему равно значение установившейся ошибки e_у=lim_|t→∞ e(t) ?

Рассчитать, используя теорему преобразования Лапласа о конечном значении оригинала.

e_у=lim_|t→∞ e(t) = lim_|s→0 E(s) = lim_|s→0 F(s) Φ_e(s) =

= lim_|s→0 s *(1/s) * (0.2s² + 1.2s + 1)/ (0.2s² + 1.2s + 41)= 0,02439


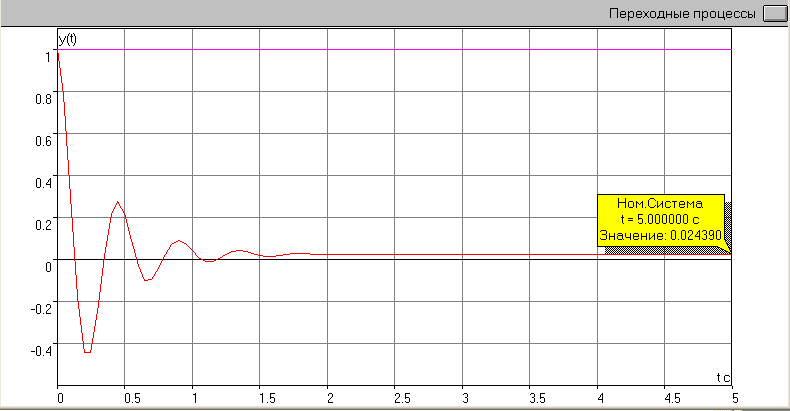
Расчет установившейся ошибки по результатам эксперимента:

e_y = 0.02439

Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
Записать формулу e_y = f(K), выражающую зависимость установившейся ошибки от контурного усиления в статической системе при постоянном входном сигнале.

e_у = K/(K + 1).

1.11. На вход исследуемой системы подается воздействие с постоянной скоростью f(t)=at=0.1t (изображение F(s)=a/s²).

Чему равно значение установившейся ошибки e_у=lim_|t→∞ e(t) ?

Рассчитать, используя теорему преобразования Лапласа о конечном значении оригинала.

e_у=lim_|t→∞ e(t) = lim_|s→0 E(s) = lim_|s→0 F(s) Φ_e(s) = ∞

Графики процессов входного воздействия f(t) и выхода y(t).



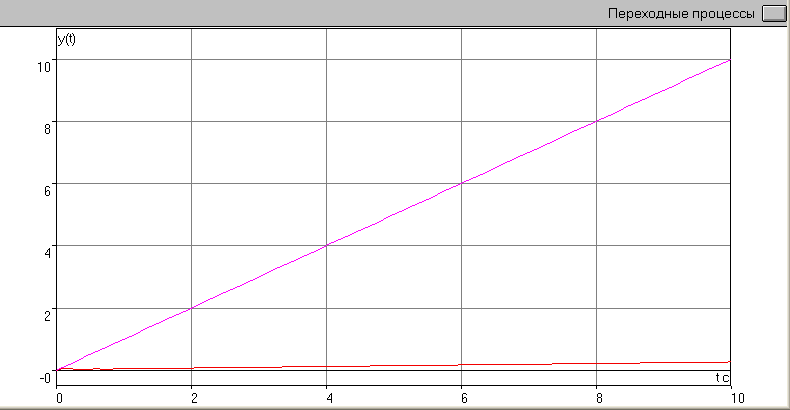
По графику видно, что e_у=lim_|t→∞ e(t) = ∞

Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
Вывод о возможности (или невозможности) “отработки” любой статической системой входных сигналов, изменяющихся с постоянной скоростью.
“Отработка” любой статической системой входных сигналов, изменяющихся с постоянной скоростью невозможна, т.к. в некоторых случаях установившейся ошибка e_у=lim_|t→∞ e(t) = ∞

Задание 2

Исследование астатической системы управления 2-го порядка

Рассматриваемые в задании темы:

• 
  Передаточная функция разомкнутой системы.
  
• 
  Передаточные функции по управлению и по ошибке замкнутой системы.
  
• 
  Точность СУ в установившемся режиме. Расчет установившихся ошибок.
  

2.1. Модель СУ №2 задана структурной схемой  рис.2.1. Модель имеет такую же структуру, как и СУ №1; отличается операторами звеньев.

Р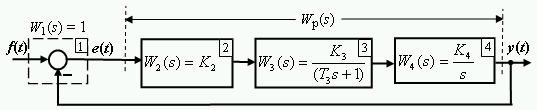
ис. 2.1
Звено 1 – “сумматор” с ПФ W₁(s) = 1.

Значения параметров ПФ остальных звеньев:

W₂(s)=K_2=20;

W₃(s)=K₃/(T₃s+1)=1/(2s+1);

W₄(s)=K₄/s=0.1/s .

2.2. Почему данная СУ называется “астатическая”?

Обоснование:

Т.к. установившиеся ошибка будет равна 0.

2.3. Сформировать модель системы с использованием графического редактора программы CLASSiC. Модель сохранить в файле, присвоив ей конкретное имя.

В
ид структурной схемы из графического редактора программы CLASSiC изображен на рис. 2.2.

Рис. 2.2

Модель: "C:\DOCUME1\93351\00161\OTY\CLASSIC3\MODEL2.MDL"

==================================

Количество блоков: 4

Количество связей: 4
=========================================================

| | Передаточные функции | |

| Блоки |-------------------------------| Связи |

| | Числитель |Знаменатель|Степень| |

=========================================================

| #1 | 1 | 1 | 0 | 2 |

| Вход | | | | |

|------------|-----------|-----------|-------|----------|

| #2 | 20 | 1 | 0 | 3 |

|------------|-----------|-----------|-------|----------|

| #3 | 1 | 1 | 0 | 4 |

| | | 2 | 1 | |

|------------|-----------|-----------|-------|----------|

| #4 | 0.1 | 0 | 0 | -1 |

| Выход | | 1 | 1 | |

=========================================================
2.4. Общая структура, к которой может быть приведена исследуемая модель, представлена на рис. 1.3.

Вычислить значение контурного усиление исследуемой СУ:

K = K₂ K₃ K₄ = 20*1*0.1= 2

2.5. Выразить через численные значения параметров звеньев передаточную функцию W_P(s)= B_P(s)/A_P(s) разомкнутой СУ.

W_P(s)= 2/(2s² + s). (2.2)

Результат автоматизированного расчета:

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 2 | 0 | 0 |

| | | 1 | 1 |

| | | 2 | 2 |
Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.

2.6. Записать через численные значения параметров звеньев ПФ по управлению Ф(s)=Y(s)/F(s) замкнутой системы.

Ф(s)= 2/(2s² + s + 2). (2.3)
================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 2 | 2 | 0 |

| | | 1 | 1 |

| | | 2 | 2 |

Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
2.7. Записать через численные значения параметров звеньев ПФ по ошибке Ф_e(s)=E(s)/F(s) для этой системы.

Ф_e(s)= (2s² + s)/(2s² + s + 2).

Результат автоматизированного расчета:

================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 0 | 2 | 0 |

| | 1 | 1 | 1 |

| | 2 | 2 | 2 |
Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
2.8. На вход исследуемой системы подается единичное ступенчатое воздействие f(t)=1(t) (изображение этой функции F(s) = 1/s).

Чему равно значение установившейся ошибки e_у=lim_|t→∞ e(t) ?

Рассчитать, используя теорему преобразования Лапласа о конечном значении оригинала.

e_у=lim_|t→∞ e(t) = lim_|s→0 E(s) = lim_|s→0 F(s) Φ_e(s) =

= lim_|s→0 s *(1/s) * (2s² + s)/(2s² + s + 2)= 0

(2.5)

График процессов в системе для передачи по управлению , где показано установившееся значение выходной координаты y(t).


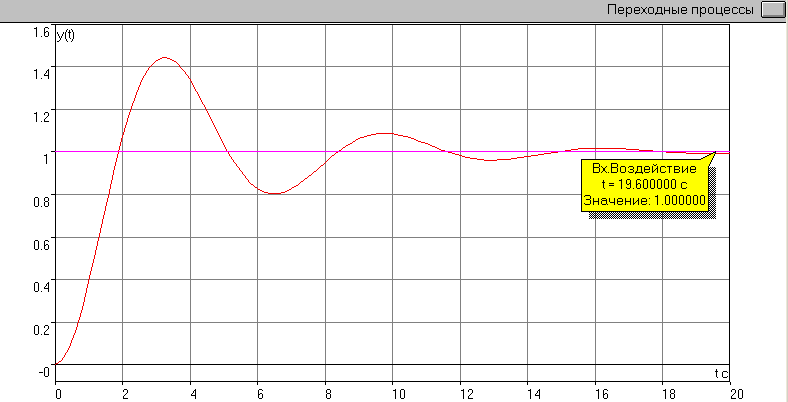
Рис. 2.3

Расчет установившейся ошибки по результатам эксперимента:

e_у = f(t) – y_у(t) = 1 – 1 = 0.

Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.

Вывод о характере зависимости установившейся ошибки от контурного усиления и других параметров астатической системы при отработке постоянного входного сигнала:
Т.к. система является астатической, то мы видим, что установившиеся ошибка равна 0.
2.9. На вход исследуемой системы подается воздействие с постоянной скоростью f(t)=at=0.1t (изображение F(s)=a/s²).

Чему равно значение установившейся ошибки e_у=lim_|t→∞ e(t) ?

Рассчитать, используя теорему преобразования Лапласа о конечном значении оригинала.