ТАУ. Практикум по курсу "Основы теории управления" Вариант 22 Хахалев А. Д. Ст гр. 6894

• Название: Практикум по курсу "Основы теории управления" Вариант 22 Хахалев А. Д. Ст гр. 6894
• Дата: 08.06.2022
• Размер: 421 Kb.
• Имя файла: 6257579.doc
• Тип: Практикум; #576629
• страница: 4 из 4

p1 = -0.500000

p2 = -10.000000

p3 = -10.000000
Вид корневой плоскости представлен на рис. 4.3.


Вывод об устойчивости СУ по корням ХП:
Судя по корням ХП CУ устойчива.



Вывод об устойчивости СУ по виду переходного процесса:
Судя по виду переходного процесса CУ устойчива.
Вывод о совпадении результатов “ручного” и автоматизированного расчетов:
Расчёты совпадают.
4.5. Определить “критический” коэффициент усиления в контуре обратной связи. Использовать критерий Гурвица для полиномов 3-го порядка. Привести необходимые вычисления и обосновать ответ

= a₂/ a₃=0.41/0.02 = 20.5 (4.7)
Автоматизированный анализ устойчивости.

Полюсы ПФ системы (корни полинома знаменателя ПФ):
p1 = -24.449090

p2 = 1.974545 +14.235618j

p3 = 1.974545 -14.235618j


Рис. 4.5

Вывод о нахождении СУ на границе устойчивости по корням ХП:
СУ находится на границе устойчивости по корням ХП


Рис. 4.6

Вывод нахождении СУ на колебательной границе устойчивости по виду переходного процесса:
СУ находится на колебательной границе устойчивости
Вывод о совпадении результатов “ручного” и автоматизированного расчетов:

Расчеты совпадают

4.6. Для контурного усиления K записать область устойчивости – интервал значений (K_minKK_max), при котором данная система устойчива.

0K (4.9)

Обоснование:

Т.к. все коэффициенты положительны при (0K)
Задание 5

Исследование устойчивости астатической системы управления 3-го порядка.

Алгебраические критерии устойчивости

Рассматриваемые в задании темы:

• 
  Характеристический полином (ХП) замкнутой системы.
  
• 
  Связь коэффициентов ХП с параметрами модели СУ.
  
• 
  Алгебраический критерий устойчивости для систем 3-го порядка.
  
• 
  Критический коэффициент усиления в контуре обратной связи.
  

5.1. Модель СУ №4 задана структурной схемой  рис.5.1.

Р
ис. 5.1
Операторы звеньев:

Звено 1 – “сумматор”. Его ПФ W₁(s) = K₁ = 1.

Значения параметров ПФ остальных звеньев:

W₂(s)=K_2=10;

W₃(s)=K₃/(T₃s+1)=2/(s+1);

W₄(s)=K₄/(T₄s+1)=1/(0.1s+1);

W₅(s)=K₅/(T₅s+1)=0.1/s.
5.2. С использованием графического редактора программы CLASSiC сформировать модель системы в соответствии с заданием 4.1. Модель сохранить в новом файле.

Вид структурной схемы из графического редактора программы CLASSiC приведен на рис. 4.2.

Модель: "C:\DOCUME1\93351\00161\OTY\CLASSIC3\MODEL4.MDL"

==================================

Количество блоков: 5

Количество связей: 5
=========================================================

| | Передаточные функции | |

| Блоки |-------------------------------| Связи |

| | Числитель |Знаменатель|Степень| |

=========================================================

| #1 | 1 | 1 | 0 | 2 |

|------------|-----------|-----------|-------|----------|

| #2 | 10 | 1 | 0 | 3 |

|------------|-----------|-----------|-------|----------|

| #3 | 2 | 1 | 0 | 4 |

| | | 1 | 1 | |

|------------|-----------|-----------|-------|----------|

| #4 | 1 | 1 | 0 | 5 |

| | | 0.1 | 1 | |

|------------|-----------|-----------|-------|----------|

| #5 | 0.1 | 0 | 0 | 1 |

| | | 1 | 1 | |
5.3. Найти (вычислить) и записать: значение контурного усиления K, ХП A_P(s) разомкнутой СУ, ХП A(s) замкнутой системы, ПФ по управлению Ф(s) замкнутой системы.

K = 2

A_P(s) = 0.1s³ + 1.1 s² + 1

A (s) = a₃s³+ a₂s²+ a₁s+ a₀ = 1 + B_P(s)/A_P(s)

Ф(s) = 2 / (0.1s³ + 1.1 s² + 1)

Результат автоматизированного расчета:
================================================

| | Передаточные функции |

| Система |-------------------------------|

| | Числитель |Знаменатель|Степень|

================================================

| Ном.Система | 2 | 0 | 0 |

| | | 1 | 1 |

| | | 1.1 | 2 |

| | | 0.1 | 3

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

Расчёты совпадают.

5.4. Используя критерий устойчивости Гурвица, проанализировать устойчивость исследуемой системы:

1. 
   Устойчива;
   
2. 
   Неустойчива;
   
3. 
   Находится на нейтральной границе устойчивости;
   
4. 
   Находится на колебательной границе устойчивости.
   

Обоснование ответа: Все три корня левые - система устойчива

1,1>0, а_2*а₁>а_3*а₀
Автоматизированный анализ устойчивости.

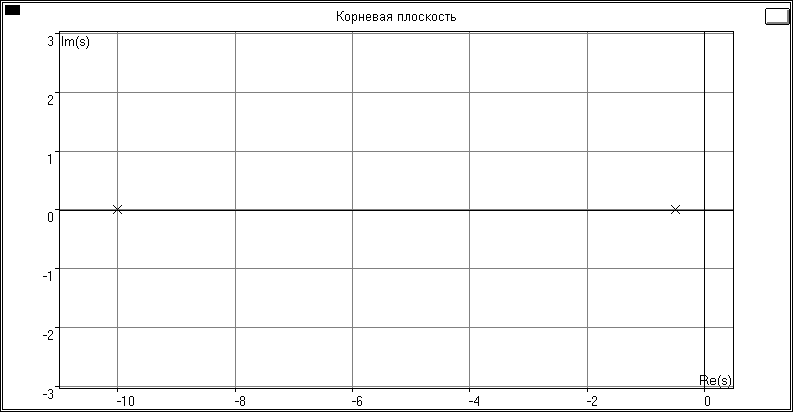
Полюсы ПФ системы (корни полинома знаменателя ПФ; он же – ХП системы):

p1 = 0.000000

p2 = -1.000000 (5.5)

p3 = -10.000000

Вид корневой плоскости представлен на рис. 5.2.

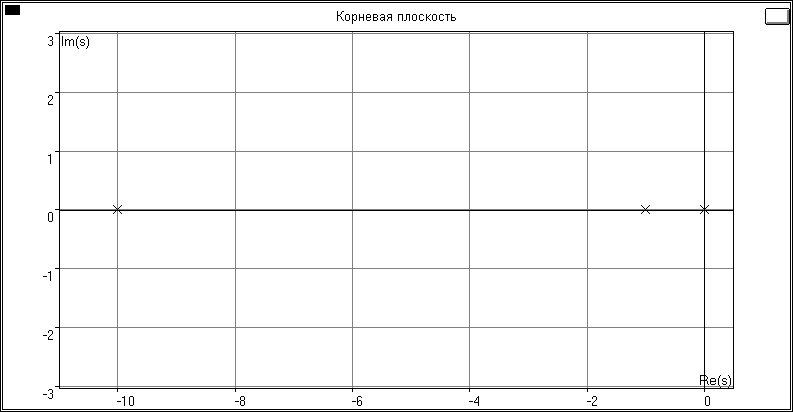Рис. 5.2

Вывод об устойчивости СУ по корням ХП:
Судя по корням ХП CУ устойчива.



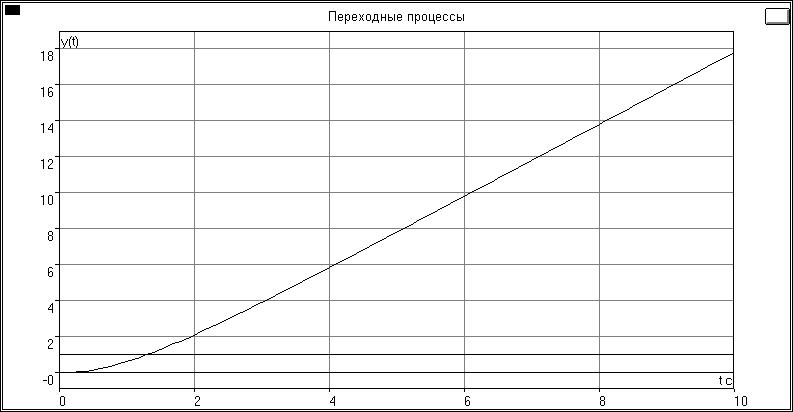
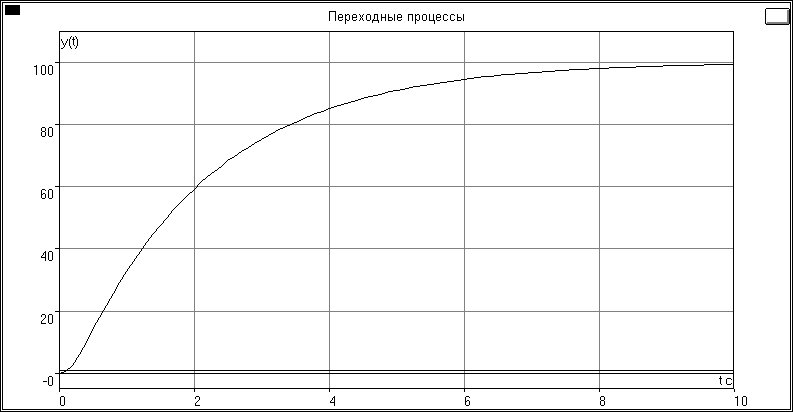
Рис. 5.3

Вывод об устойчивости СУ по виду переходного процесса:
Судя по виду переходного процесса CУ устойчива.
Вывод о совпадении результатов “ручного” и автоматизированного расчетов:
Расчёты совпадают.
5.5. Определить “критический” коэффициент усиления в контуре обратной связи. Использовать критерий Гурвица для полиномов 3-го порядка. Привести необходимые вычисления и обосновать ответ

= a₂/ a₃=1.1/0.1 = 11

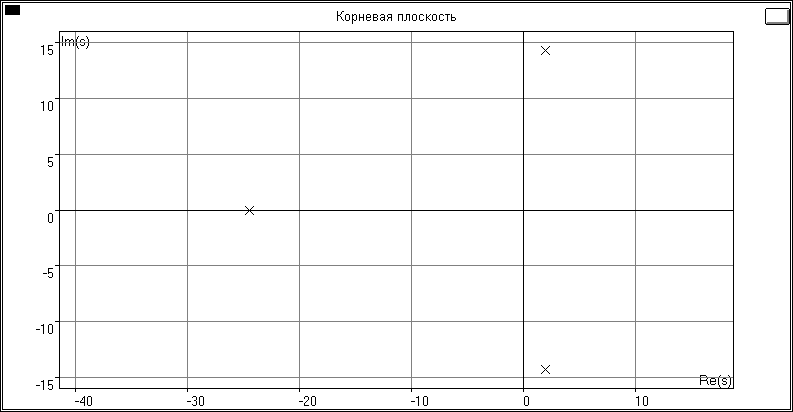
Автоматизированный анализ устойчивости.

Полюсы ПФ системы (корни полинома знаменателя ПФ):

p1 = -0.393712 +1.342893j

p2 = -0.393712 -1.342893j

p3 = -10.212576



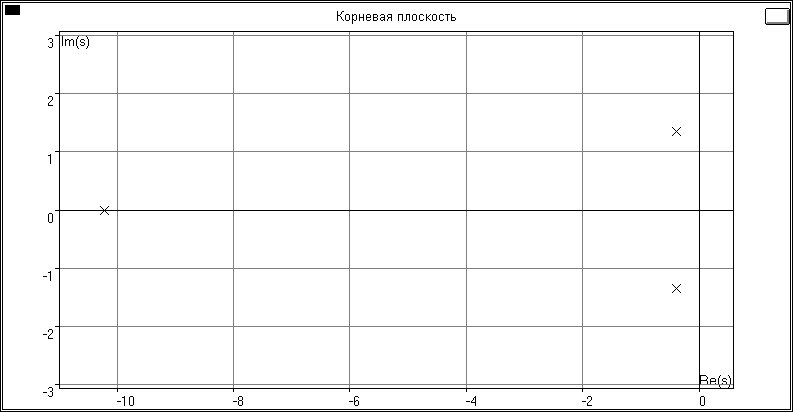
Рис. 5.4

Вывод о нахождении СУ на границе устойчивости по корням ХП:
Судя по корням ХП СУ устойчива


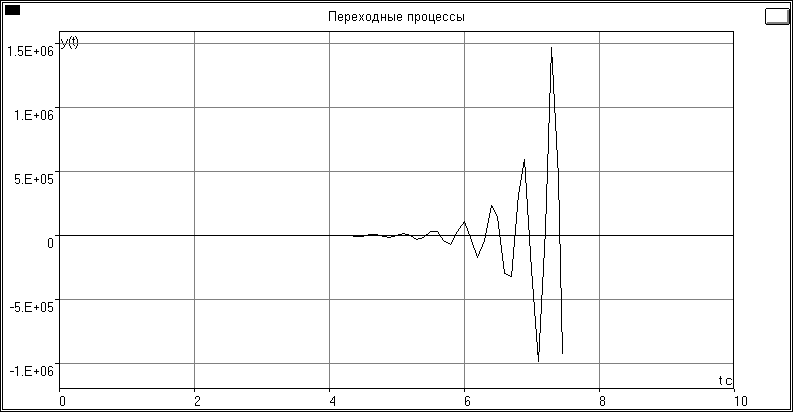
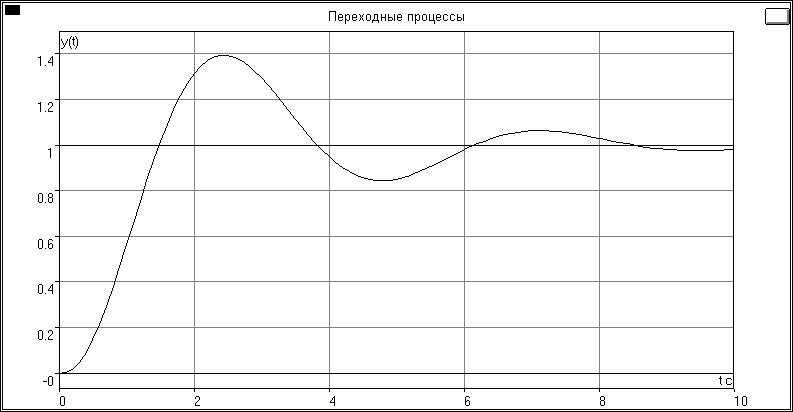Рис. 5.5

Вывод о нахождении СУ на колебательной границе устойчивости по виду переходного процесса:
Судя по виду переходного процесса CУ устойчива.

Вывод о совпадении результатов “ручного” и автоматизированного расчетов:

Расчёты совпадают.
5.6. Для контурного усиления K записать область устойчивости – интервал значений (K_minKK_max), при котором данная система устойчива.

0K (5.8)

Обоснование:
Т.к. все коэффициенты положительны при (0K)

Задание 6

Исследование устойчивости систем управления.

Частотные критерии устойчивости

Рассматриваемые в задании темы:

• 
  Построение логарифмических частотных характеристик СУ;
  
• 
  Частотный критерий устойчивости Найквиста;
  
• 
  Количественные оценки запасов устойчивости.
  

Частотные критерии позволяют судить об устойчивости СУ по виду ее частотных характеристик.

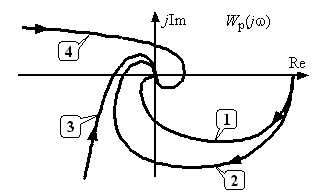
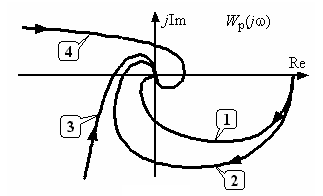
По критерию устойчивости Найквиста определяется устойчивость замкнутой системы по частотным характеристикам разомкнутой системы!!!

Критерий устойчивости Найквиста сформулирован на амплитудно-частотных характеристиках (АЧХ) разомкнутой системы.

Имеется также интерпретация критерия Найквиста для логарифмических частотных характеристик (ЛЧХ).

Связь вида ЛЧХ и параметров СУ дает построение асимптотической ЛЧХ.

Критерий устойчивости Найквиста позволяет ввести количественные оценки запасов устойчивости.

6.1.Исследование устойчивости статической системы управления 3-го порядка

Используется модель анализируемой СУ, заданная в пп. 4.1 и 4.2.

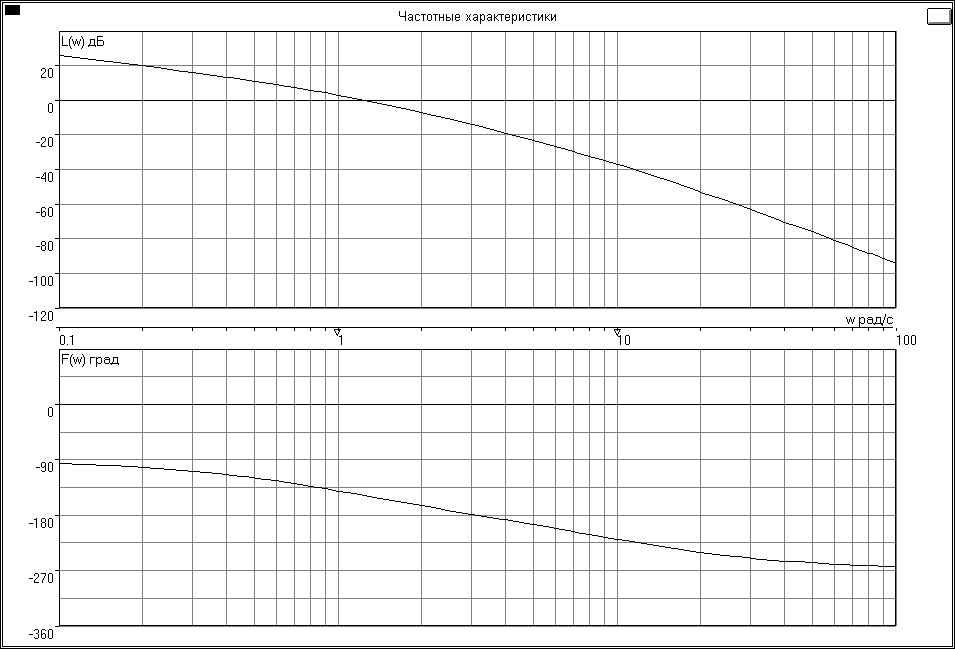
6.1.1. Построить с использованием программы CLASSiC амплитудную L_р() и фазовую _р() логарифмические частотные характеристики разомкнутой системы.

Скопировать график в данный отчет. На этом же графике с помощью средств рисования WORD построить асимптотическую ЛАХ, обозначить графики и показать запас по фазе (если система устойчива).

На рис.6.1 приведены результаты расчета и требуемые построения.

6.1.2. По рис.6.1 проанализировать устойчивость исследуемой СУ:

1. 
   Система устойчива;
   
2. 
   Система находится на колебательной границе устойчивости;
   
3. 
   Система неустойчива.
   

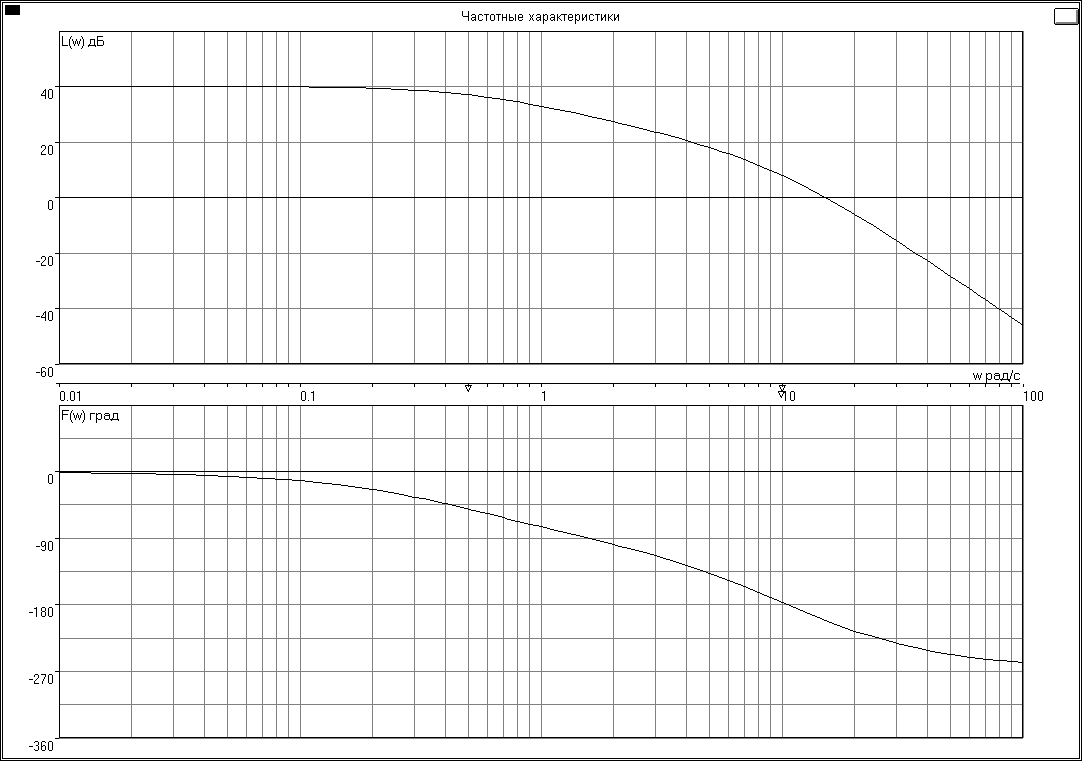
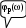
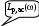
Рис. 6.1

6.1.3. Определить по рис. 6.1. следующие частотные показатели качества
Частота среза ω_ср = 15 рад/с

Запас по фазе Δφ = -22 град

Частота “пи” ω_π = 11 рад/с

Запас по модулю ΔL = -7 дБ
Результат автоматизированного расчета:

Модель: "C:\DOCUME1\93351\00161\OTY\CLASSIC3\MODEL3_1.MDL"

==================================

Ном.Система

Частота среза: 15.1564 рад/с

Запас по фазе: -21.2777 град

Частота пи: 10.4881 рад/с

Запас по модулю: -7.1112 дБ
Вывод о соответствии результатов ручного и автоматизированного расчетов частотных показателей качества:
Расчёты совпадают
6.1.4. Используя полученные в пп. 6.1.1 – 6.1.3 построения и данные, вычислить значение критического коэффициента усиления в контуре системы:

20Lg K_кр =20Lg 20.5 = 26,23 дБ;

K_кр = 20,5

Вывод о соответствии результатов расчета критического значения контурного усиления по алгебраическому и частотному критериям:

Расчёты соответствуют
6.1.5. На рис.6.2 качественно построены амплитудно-фазовые частотные характеристики W_P(j) разных разомкнутых СУ.

Р
ис. 6.2

Которая из этих характеристик соответствует системе, анализируемой в задаче 6.1 ?

1; 2; 3; 4.

6.2.Исследование устойчивости астатической системы управления 3-го порядка

Используется модель анализируемой СУ, заданная в пп. 5.1 и 5.2.

6.2.1. Построить с использованием программы CLASSiC амплитудную L_р() и фазовую _р() логарифмические частотные характеристики разомкнутой системы.

Скопировать график в данный отчет. На этом же графике с помощью средств рисования WORD построить асимптотическую ЛАХ, обозначить графики и показать запас по фазе (если система устойчива).
Рис.6.3

На рис.6.3 приведены результаты расчета и требуемые построения.

6.2.2. По рис.6.3 проанализировать устойчивость исследуемой СУ:

1. 
   Система устойчива;
   
2. 
   Система находится на колебательной границе устойчивости;
   
3. 
   Система неустойчива.
   

Вывод о соответствии результату анализа устойчивости, полученному по алгебраическому критерию:

Расчёты соответствуют
6.2.3. Определить по рис. 6.3. следующие частотные показатели качества:
Частота среза ω_ср = 2 рад/с

Запас по фазе Δφ = 30 град

Частота “пи” ω_π = 3 рад/с

Запас по модулю ΔL = 15 дБ
Результат автоматизированного расчета:
"C:\DOCUME1\93351\00161\OTY\CLASSIC3\MODEL4_1.MDL"

==================================

Ном.Система

Частота среза: 1.2437 рад/с

Запас по фазе: 31.7124 град

Частота пи: 3.1623 рад/с

Запас по модулю: 14.8073 дБ

Вывод о соответствии результатов ручного и автоматизированного расчетов частотных показателей качества:

Расчёты совпадают
6.2.4. Используя полученные в пп. 6.2.1 – 6.2.3 построения и данные, вычислить значение критического коэффициента усиления в контуре системы:

20Lg K_кр = 20Lg 11= 20,8 дБ;

K_кр = 11

Вывод о соответствии результатов расчета критического значения контурного усиления по алгебраическому и частотному критериям:

Расчёты соответствуют
6.2.5. На рис.6.4 качественно построены амплитудно-фазовые частотные характеристики W_P(j) разных разомкнутых СУ.

Рис.6.4


Которая из этих характеристик соответствует системе, анализируемой в задаче 6.2 ?

1; 2; 3; 4.

Выводы по лабораторному практикуму 1

Было проведено исследование статической системы управления 2-го порядка, астатической системы управления 2-го порядка. Ознакомились с алгебраическими критериями устойчивости. Провели исследование устойчивости статической системы управления 2-го и 3-го порядка. Ознакомились с частотными критериями устойчивости. В большинстве своем автоматические и ручные расчеты совпадают.