eу=lim|t→∞ e(t) = lim|s→0 E(s) = lim|s→0 F(s) Φe(s) =
= lim|s→0 s *(1/ s2) * (2s2 + s)/(2s2 + s + 2)= 0.5 (2.7)
График процессов входного воздействия f(t) и выходной координаты y(t).
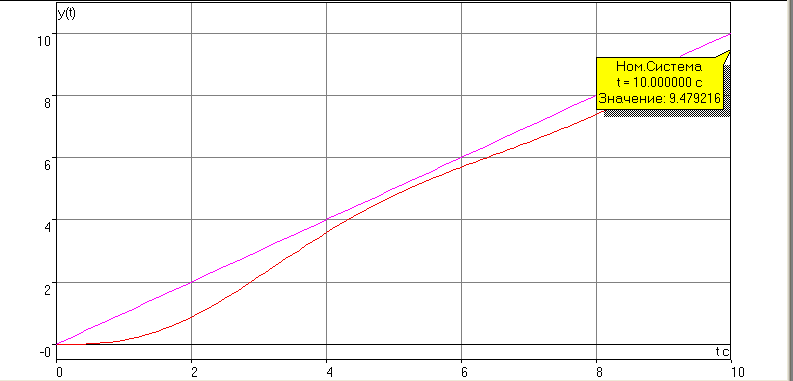
Рис. 2.4
eу≈0.5 . (2.8)
Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
Записать формулу eу = f(a, K), выражающую зависимость установившейся ошибки от скорости входного сигнала и контурного усиления в астатической системе при входном сигнале с постоянной скоростью.
eу = 1/K.
Вывод о возможности (или невозможности) “отработки” любой астатической системой входных сигналов, изменяющихся с постоянной скоростью
“Отработка” любой астатической системой входных сигналов, изменяющихся с постоянной скоростью возможна.
Задание 3
Исследование устойчивости систем управления 2-го порядка.
Алгебраические критерии устойчивости
Рассматриваемые в задании темы:
Характеристический полином (ХП) замкнутой системы.
Связь коэффициентов ХП с параметрами модели СУ.
Алгебраический критерий устойчивости для систем 2-го порядка.
Для устойчивости динамической системы, описываемой линейным дифференциальным уравнением, необходимо и достаточно, чтобы все действительные корни характеристического полинома были отрицательными, а все пары комплексно сопряженных корней имели бы отрицательную действительную часть. При размещении таких корней на комплексной плоскости они располагаются в левой её части, т.е. слева от мнимой оси. Поэтому говорят, что устойчивая система должна иметь все “левые” корни ХП.
Для определения устойчивости СУ следует либо произвести расчет корней ХП, либо применить “критерии устойчивости ”.
Критерии устойчивости позволяют судить о принадлежности корней полинома левой части комплексной плоскости без вычисления корней полинома.
Алгебраические критерии устойчивости основаны на анализе соотношения коэффициентов полинома.
Устойчивость замкнутой СУ определяется по характеристическому полиному именно замкнутой системы, т.е. системы с обратной связью!!!
3.1. Исследование устойчивости статической системы
Модель исследуемой системы приведена в задании 1, п. 1.1.
Для анализируемой системы необходимые сведения о характеристическом полиноме и его вычислении приведены в п.1.5 и п.1.6.
В соответствии с выражением (1.10):
A(s) = AP(s) + BP(s) = a2s2+ a1s+ a0 = (a2,рs2+ a1,рs+ a0,р ) + b0. (3.1)
В результате, для рассматриваемой статической системы ХП выражается через параметры модели следующим образом
A(s) = T3T4s2 + (T3 + T4)s + K+1, (3.2)
где
a2 = a2,р = T3T4,
a1 = a1,р = (T3 + T4),
a0 = a0,р + K = K+1.
Из этих соотношений видно, что в анализируемой статической системе “старший” a2 и “средний” a1 коэффициенты ХП замкнутой системы совпадают с соответствующими коэффициентами a2,р и a1,р ХП разомкнутой системы и зависят только от инерционностей, т.е. от постоянных времени.
“Младший” коэффициент
a0 = K+1 (3.3)
определяется только контурным усилением.
Записать выражение для ХП замкнутой системы в числовом виде:
AP(s) = 0.2s2 + 1.2s + 41.
Для контурного усиления определить область устойчивости – интервал значений (KminKKmax), при котором рассматриваемая система устойчива.
1: (0K1.25); 2: (0K100); 3: (0K); 4: (K).
Обоснование: При (0 <K) система устойчива, это следует из необходимого условия устойчивости, т.к. имеем полином второго порядка, то это необходимое условие устойчивости также является и достаточным.
3.2. Исследование устойчивости астатической системы
Модель исследуемой системы приведена в задании 2, п. 2.1.
ХП анализируемой разомкнутой СУ
AP(s) = a2,рs2+ a1,рs+ a0,р = (T3s+1)s = T3 s2+s. (3.5)
При этом
a2,р = T3,
a1,р = 1,
a0,р = 0.
В соответствии с выражением (1.10) и (3.1) для рассматриваемой астатической системы ХП выражается через параметры модели следующим образом:
A(s) = a2s2+ a1s+ a0 = T3s2 + s + K, (3.6)
где
a2 = a2,р = T3,
a1 = a1,р = 1,
a0 = K.
Из этих соотношений видно, что в анализируемой астатической системе “старший” a2 и “средний” a1 коэффициенты ХП замкнутой совпадают с соответствующими коэффициентами a2,р и a1,р ХП разомкнутой системы. Коэффициент a2,р зависит только от постоянной времени, а a1,р = Const = 1.
“Младший” коэффициент
a0 = K (3.7)
равен значению контурного усиления (см. различие со статической системой – (3.3)).
Записать выражение для ХП замкнутой системы в числовом виде.
AP(s) = 2s2 + s + 2.
Для контурного усиления определить область устойчивости – интервал значений (KminKKmax), при котором данная система устойчива.
1: (0K1.25); 2: (0K100); 3: (0K); 4: (K).
Обоснование: При (0 <K) система устойчива, это следует из необходимого условия устойчивости, т.к. имеем полином второго порядка, то это необходимое условие устойчивости также является и достаточным.
Задание 4
Исследование устойчивости статической системы управления 3-го порядка.
Алгебраические критерии устойчивости
Рассматриваемые в задании темы:
Характеристический полином (ХП) замкнутой системы.
Связь коэффициентов ХП с параметрами модели СУ.
Алгебраический критерий устойчивости для систем 3-го порядка.
Критический коэффициент усиления в контуре обратной связи.
4.1. Модель СУ №3 задана структурной схемой рис.4.1.
 Рис. 4.1 Рис. 4.1
Звено 1 – “сумматор”. Его ПФ W1(s) = K1 = 1.
Значения параметров ПФ остальных звеньев:
W2(s)=K2=20;
W3(s)=K3/(T3s+1)=10/(2s+1);
W4(s)=K4/(T4s+1)=0.5/(0.1s+1);
W5(s)=K5/(T5s+1)=1/(0.1s+1).
4.2. С использованием графического редактора программы CLASSiC сформировать модель системы в соответствии со структурной схемой рис.4.1 и заданными операторами звеньев. Модель сохранить в файле, присвоив ей конкретное имя.
В
ид структурной схемы из графического редактора программы CLASSiC приведен на рис. 4.2.
Рис. 4.2
Модель в текстовой форме.
Модель: "C:\DOCUME
1\9335
1\0016
1\OTY\CLASSIC3\MODEL3_2.MDL"
==================================
Количество блоков: 5
Количество связей: 5
=========================================================
| | Передаточные функции | |
| Блоки |-------------------------------| Связи |
| | Числитель |Знаменатель|Степень| |
=========================================================
| #1 | 1 | 1 | 0 | 2 |
| Вход | | | | |
|------------|-----------|-----------|-------|----------|
| #2 | 20 | 1 | 0 | 3 |
|------------|-----------|-----------|-------|----------|
| #3 | 10 | 1 | 0 | 4 |
| | | 2 | 1 | |
|------------|-----------|-----------|-------|----------|
| #4 | 0.5 | 1 | 0 | 5 |
| | | 0.1 | 1 | |
|------------|-----------|-----------|-------|----------|
| #5 | 1 | 1 | 0 | -1 |
| Выход | | 0.1 | 1 | |
4.3. Найти (вычислить) и записать: значение контурного усиления K, ХП AP(s) разомкнутой СУ, ХП A(s) замкнутой системы, ПФ по управлению Ф(s) замкнутой системы.
K = 20*10*0,5*1=100.
AP(s) = 0.02s3 + 0.41 s2 + 2.02 s +1
A (s) = a3s3+ a2s2+ a1s+ a0 = 1 + BP(s)/AP(s).
Ф(s) = 100 / (0.02s3 + 0.41 s2 + 2.02 s +1 )
Результат автоматизированного расчета:
================================================
| | Передаточные функции |
| Система |-------------------------------|
| | Числитель |Знаменатель|Степень|
================================================
| Ном.Система | 100 | 1 | 0 |
| | | 2.2 | 1 |
| | | 0.41 | 2 |
| | | 0.02 | 3 |
Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
4.4. Используя критерий устойчивости Гурвица, проанализировать устойчивость исследуемой системы:
Устойчива;
Неустойчива;
Находится на нейтральной границе устойчивости;
Находится на колебательной границе устойчивости.
Обоснование ответа:
Значит все три корня левые и система устойчива
0,902>0,02, а2*а1 > а3*а0
Автоматизированный анализ устойчивости:
Полюсы ПФ системы (корни полинома знаменателя ПФ; он же – ХП системы):
|
 Скачать 421 Kb.
Скачать 421 Kb.

 Рис. 4.1
Рис. 4.1