ОТУ Лабораторный практикум Вариант 22
ОФ
Заочное отделение
Кафедра Автоматики и процессов управления
Лабораторный практикум по курсу
“Основы теории управления”
Вариант № 22 Выполнил: Хахалев А.Д. Ст. гр. 6894 Преподаватель:
СПбГЭТУ «ЛЭТИ»
2018 г.
Задание 1
Исследование статической системы управления 2-го порядка
Рассматриваемые в задании темы:
Передаточная функция разомкнутой системы;
Характеристические полиномы разомкнутой и замкнутой системы;
Передаточные функции по управлению и по ошибке замкнутой системы;
Точность СУ в установившемся режиме. Расчет установившихся ошибок.
1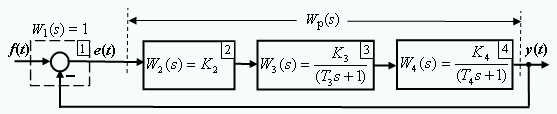
.1. Модель СУ №1 представлена структурной схемой рис.1.1.
Рис. 1.1
Операторы звеньев (блоков) заданы передаточными функциями (ПФ).
Звено 1 – “сумматор”. Его ПФ W1(s) = K1 = 1 = 1/1.
Значения параметров ПФ остальных звеньев:
W2(s)=K2=10 = 10/1;
W3(s)=K3/(T3s+1)=2/(s+1);
W4(s)=K4/(T4s+1)=2/(0.2s+1).
1.2. К какому классу (классам) относится математическая модель СУ ?
1: линейные; 2: непрерывные; 3: дискретные, 4: нелинейные.
Почему данная СУ называется “статическая” ?
Обоснование: Т.к в 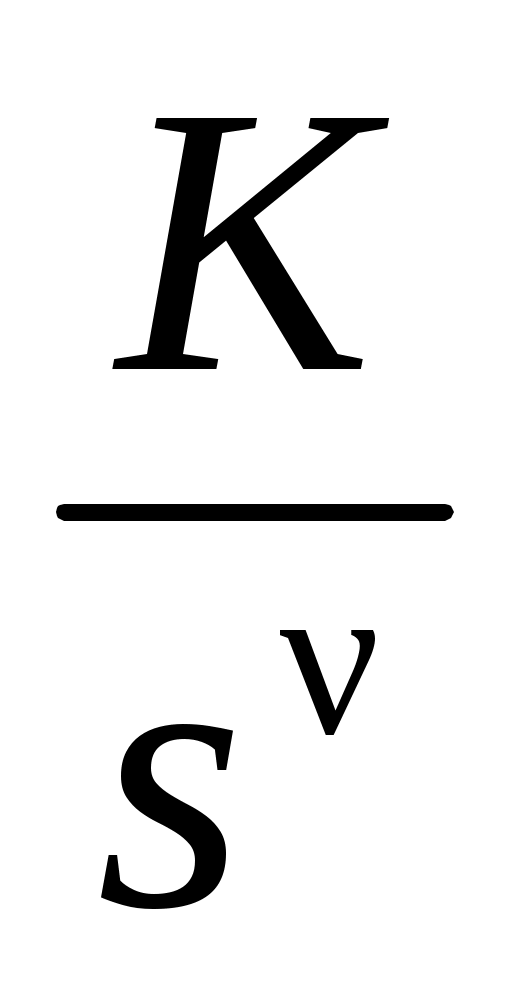 в нашем случае v = 0; Имеется обратная связь. в нашем случае v = 0; Имеется обратная связь.
1.3. Какой принцип управления реализован в данной СУ?
1принцип разомкнутого управления,
2 принцип компенсации,
3принцип замкнутого управления (принцип обратной связи),
4 принцип комбинированного управления (одновременная реализация в СУ принципов 2 и 3).
1.4. С использованием графического редактора программы CLASSiC сформировать модель системы в соответствии со структурной схемой рис.1.1 и заданными операторами звеньев. Модель сохранить в файле, присвоив ей конкретное имя.
В
ид структурной схемы из графического редактора программы CLASSiC приведен на рис. 1.2.
Рис. 1.2
Модель: "C:\DOCUME1\93351\00161\OTY\CLASSIC3\MODEL1.MDL"
==================================
Количество блоков: 4
Количество связей: 4
=========================================================
| | Передаточные функции | |
| Блоки |-------------------------------| Связи |
| | Числитель |Знаменатель|Степень| |
=========================================================
| #1 | 1 | 1 | 0 | 2 |
| Вход | | | | |
|------------|-----------|-----------|-------|----------|
| #2 | 10 | 1 | 0 | 3 |
|------------|-----------|-----------|-------|----------|
| #3 | 2 | 1 | 0 | 4 |
| | | 1 | 1 | |
|------------|-----------|-----------|-------|----------|
| #4 | 2 | 1 | 0 | -1 |
| Выход | | 0.2 | 1 | |
=========================================================
1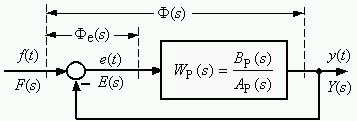
.5. На рис.1.3 показана общая структура, которая получена из модели, представленной на рис. 1.1.
Рис. 1.3
Полином числителя ПФ разомкнутой СУ BP(s) = b0 = K2 K3 K4 = K,
“Контурное усиление” K системы – произведение статических коэффициентов передач всех звеньев контура, образованного обратной связью. Рассматриваемая модель СУ – с единичной обратной связью. Так как сумматор также имеет единичный коэффициент передачи K1 = 1, то контурное усиление в нашем случае равно произведению коэффициентов передач всех звеньев прямой цепи.
Вычислить значение контурного усиление исследуемой СУ:
K = K2 K3 K4 = 10*2*2=40 (1.1)
Полином числителя ПФ исследуемой разомкнутой СУ BP(s) = b0 = K – совпадает со значением контурного усиления для исследуемой системы.
“Характеристический полином разомкнутой системы” AP(s) – знаменатель ПФ WP(s) системы без обратной связи. Для СУ с единичной обратной связью AP(s) представляет собой произведение полиномов знаменателей передаточных функций звеньев прямой цепи.
Для исследуемой системы в общем виде
AP(s) = (T3s+1)(T4s+1) (1.2)
При представлении полинома в стандартном виде
AP(s) = a2,рs2+ a1,рs+ a0,р = T3T4s2 + (T3 + T4)s + 1, (1.3)
где:
a2,р = T3T4,
a1,р = (T3 + T4),
a0,р = 1.
Записать в численном виде характеристический полином разомкнутой системы:
AP(s) = 0.2s2 + 1.2s + 1. (1.4)
ПФ разомкнутой СУ в общем виде:
WP(s) = BP(s)/AP(s) = K/(T3s+1)(T4s+1) =K / (T3T4s2 + (T3 + T4)s + 1). (1.5)
Выразить через параметры звеньев передаточную функцию исследуемой СУ:
WP(s)= 40/(0.2s2 + 1.2s + 1) (1.6)
Результат автоматизированного расчета:
================================================
| | Передаточные функции |
| Система |-------------------------------|
| | Числитель |Знаменатель|Степень|
================================================
| Ном.Система | 40 | 1 | 0 |
| | | 1.2 | 1 |
| | | 0.2 | 2 |
================================================
Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
1.6. Для рассматриваемой здесь одноконтурной СУ с единичной отрицательной обратной связью записать формулу, связывающую ПФ по управлению Ф(s)=Y(s)/F(s) замкнутой системы и ПФ WP(s) разомкнутой системы: Ф(s)=f(WP(s)).
Ф(s)= WP(s) / (1 + WP(s)) (1.7)
Записать формулу, связывающую ПФ по управлению Ф(s)=B(s)/A(s) замкнутой системы, где B(s) и A(s) – полиномы числителя и знаменателя этой ПФ, с полиномами числителя BP(s) и знаменателя AP(s) передаточной функции WP(s) разомкнутой системы: Ф(s)=f(BP(s), AP(s)).
Ф(s)= BP(s) / (AP(s) + BP(s)) . (1.8)
Записать соотношения, выражающие полиномы B(s) и A(s) ПФ замкнутой системы через полиномы BP(s), AP(s) ПФ разомкнутой системы:
B(s) = BP(s)/AP(s), (1.9)
A(s) = 1 + BP(s)/AP(s). (1.10)
Записать через численные значения параметров звеньев ПФ Ф(s).
Ф(s)= 40/(0.2s2 + 1.2s + 41) (1.11)
Результат автоматизированного расчета:
================================================
| | Передаточные функции |
| Система |-------------------------------|
| | Числитель |Знаменатель|Степень|
================================================
| Ном.Система | 40 | 41 | 0 |
| | | 1.2 | 1 |
| | | 0.2 | 2 |
================================================
Вывод о совпадении результата “ручного” и автоматизированного расчетов:
Расчёты совпадают.
1.7. “Характеристический полином замкнутой системы” A(s) – знаменатель ПФ Ф(s) системы с обратной связью.
Указать выражение, определяющее характеристический полином замкнутой системы через полиномы ПФ разомкнутой системы:
Для одноконтурной СУ с единичной отрицательной обратной связью характеристический полином определяется выражением
1.8. Для модели исследуемой системы записать формулу, связывающую ПФ по ошибке Фe(s)=E(s)/F(s) замкнутой системы и ПФ WP(s) разомкнутой системы: Фe(s)=f(WP(s)).
Фe(s)= 1 / (1 + WP(s)) (1.12)
Записать формулу, связывающую ПФ по ошибке Фe(s)=Be(s)/A(s) замкнутой системы, где Be(s) и A(s) – полиномы числителя и знаменателя этой ПФ, с полиномами числителя BP(s) и знаменателя AP(s) передаточной функции WP(s) разомкнутой системы: Фe(s)=f(BP(s), AP(s)).
Ф(s)= AP(s) / (BP(s) + AP(s)) (1.13)
Записать соотношения, выражающие полиномы Be(s) и A(s) ПФ замкнутой системы через полиномы BP(s), AP(s) ПФ разомкнутой системы:
|
 Скачать 421 Kb.
Скачать 421 Kb.


