диагностика. Практикум по психологии личности серия Практикум по психологии

• Название: Практикум по психологии личности серия Практикум по психологии
• Анкор: диагностика
• Дата: 09.09.2022
• Размер: 4.22 Mb.
• Имя файла: Eliseev_Praktikum_po_psihologii_lichnosti.doc
• Тип: Практикум; #669214
• страница: 40 из 49

Глава 19. Интеграция субъективных и объективных представлений о времени

§19.1. Современные психофизические представления о времени реакции

Исследования времени реакций, которые осуществляются до сих пор, особенно в связи с решением проблем инженерной или юридической психологии, являются исследованиями частными и даже, казалось бы, представляют лишь исторический, академический или чисто практический интерес. Но эти «частности» приобретают весьма актуальное значение, как только мы включаем в сферу нашего внимания не только исследуемые объекты, но и особенности реципиентов, а также исследователей этих объектов.

Объективные, то есть определяемые объектами—стимулами, реакции являются еще и реакциями субъекта, и в такой мере, что эти объективные реакции становятся весьма произвольными в буквальном смысле слова. Субъект на графиках показательных, логарифмических или степенных функций как бы присутствует на всей плоскости YOX, — и то, какого именно вида будет кривая психофизической зависимости, в конечном счете определяется установками исследователя и испытуемых, задающих условия определения времени реакций.

Тогда возникает вопрос. А действительно, какими вообще могут быть кривые этих зависимостей, если субъектам — исследователям и испытуемым — предоставить на самом деле полную свободу «передвижения» на данной плоскости YOX? При этом мы не должны терять из виду и полную нашу ответственность, как бы делегированную нам в этом случае теми учеными, материал исследования которых мы используем при такой постановке вопроса: иначе будет утрачен предмет обсуждения, то есть искомое нами определение характера психологической активности человека с помощью введения временной координаты. Поэтому в пределах нашей темы исследования «полная» свобода субъекта, видимо, определяется двумя предварительными выводами.

1) все рассмотренные кривые психофизических зависимостей следует все-таки свести к логарифмическим не потому, что закон Хика «правильнее», чем закон С. С. Стивенса, а потому, что оба эти закона, в принципе равноправные в силу их объективного значения, определенного реальными, но различными условиями, выражают меру восприятия информации человеком, а мера эта выражается логарифмически. При изменении исходных посылок эта мера может быть выражена и степенной функцией, но остановиться следует на ее общепринятом логарифмическом выражении.

2) сведение всех кривых к их логарифмическому представлению необходимо еще и потому, что энтропия и негэнтропия — также выражаются логарифмически, а эти глобальные характеристики безусловно не могут не представлять, в той или иной степени, характер психологической активности человека.

Не выходя за пределы темы нашего обсуждения в рамках временного подхода, «свобода» субъекта, конечно, заключается в кавычки, -это свобода только в проявлении временных реакций. Но как обнаружится ниже, вводимые ограничения могут быть впоследствии постепенно сняты, по мере установления необходимых для этого оснований. И тем легче будет найти подобные основания, чем более строгими являются ограничения.

Значит, необходимо привлечение дополнительных материалов именно по содержанию исследований временных реакций, причем желательно материалов современных и наиболее обобщенных. Таковыми в отечественной психологии являются, в частности, данные об изменении времени реакций различных видов, обобщенные Е. И. Бойкой представленные Б. Г. Ананьевым на фоне онтогенеза человека. Графики изменений времени реакций в связи с возрастом по данным Клапареда, Гильберта, Майлса и других исследователей, включая результаты работы А. Р. Лурия и его сотрудников, представляют собою некоторые накопленные частоты проявлений указанных реакций в диапазоне приблизительно от 200 до 500 мсек., отнесенные к возрастам от 5 до 60-80 лет.

Фактически эти графики являются результатом последовательного соединения единственных точек целого веера логарифмических кривых, характеризующих каждый отдельный возраст с точки зрения времени реакций. Логарифмические кривые соединяются единой линией, которая, в частности, и представлена Б. Г. Ананьевым на фоне кривых, полученных другими вышеупомянутыми авторами [ 1, 139].

В 90-х годах XX века, в связи со столетием со дня смерти Г. Фехнера, отечественный исследователь К. В. Бардин, старший научный сотрудник Института психологии Академии наук (г. Москва), вновь констатирует, что «пороговая проблема, по-видимому, не имеет общего решения», только «парциальное» — на путях дифференциальной психофизики» [2,135].

Но важно отметить главное; различение звука с дополнительными сенсорными характеристиками, которые привносят реципиенты, или без них обобщается К. В. Бардиным в форме построения двух логарифмических кривых, что позволяет ему подчеркнуть: «Степень выраженности такого качества, как когнитивная сложность, является разной у разных наблюдателей» [2, 135], а поэтому различной является и степень смещения кривых относительно друг друга. Таким образом, с одной стороны, вновь получает подтверждение приоритетное значение логарифмических характеристик временных реакций. А с другой прямо отстаивается значение субъектного дифференциального фактора в исследовании психофизических зависимостей, до сих пор считавшихся наиболее объективными во всей психологии.

В гораздо более общем плане появляется возможность повысить меру субъекта психофизических исследований, если расширить пределы обобщения результатов этих исследований. В таком случае нужно поставить два вопроса:

1) чем, в обобщенном представлении, логарифмические кривые отличаются от других, если они настолько устойчиво проявляются во всех исследованиях времени реакций, где субъекты или реципиенты не демонстрируют преднамеренно своей когнитивной сложности?

2) какими, опять же в обобщенном представлении, являются кривые изменения объективной стороны психофизических исследований, — кривые сигналов, если также исключить преднамеренность организации подачи сигналов с точки зрения их высоты, тембра, особенностей .включения и выключения и т. д.?

Ответы на эти два вопроса разместим по порядку от объективной стороны к стороне субъективной, то есть начнем со второго вопроса, тем более что в уже упомянутой статье К. В. Бардина приведен пример спектра сигналов, составившего объективную сторону данного психофизического исследования.

§19.2. Приоритет фактора времени в современных психологических исследованиях

На примере спектра сигналов психофизического исследования К. В. Бардина легко увидеть, что интерполирующей функцией для функции, представляющей данный спектр, является функциональная зависимость Гауссова или нормального распределения. Этот вывод можно подтвердить путем применения специальных интерполяционных формул, необходимых для вычисления промежуточных значений для более точного построения кривой нормального распределения. Хотя суть обсуждаемого вопроса не была бы искажена и при простом указании на то, что по отношению к эмпирической формуле спектра сигналов, представленного графически, единственной аппроксимирующей функцией может быть только функция, представляемая кривой нормального распределения, — это отчетливо видно непосредственно по графику эмпирической кривой, если, конечно, отвлечься от несущественных в данном контексте вариаций этой кривой, отражающих дополнительные спектральные составляющие.

Таким образом, объективная сторона психофизических исследований, в обобщенном их представлении, может безусловно рассматриваться в графической форме как кривая нормального распределения.

Чтобы ответить на вопрос о субъективной стороне этих исследований, необходимо также иметь в виду, что вообще сравнение графиков любых зависимостей, в том числе и логарифмических, рассматривается как процесс подбора эмпирической формулы, определяющей характер соответствующей эмпирической зависимости

Y = K · log X.

Определение численных значений параметров, которое необходимо при точном количественном решении вопроса о принадлежности логарифмических кривых к некоторой интерполирующей функции сводится, если нас интересует только качественное, приблизительное и общее решение, к установлению только функции аппроксимирующей.

Но установление аппроксимирующей функции, если речь идет о субъективной стороне исследований, нельзя, с одной стороны, возвратить к интерполяции, так как в этом случае не найдется искомое общее решение, с другой стороны, нельзя и вводить еще один уровень субъективности, произвольно выбирая одну из многих функций, которые могли бы равноправно иметь статус функции аппроксимирующей.

§19.3. Понятия физического и психологического времени в онтогенетических исследованиях

Необходимо обратиться к материалам обобщенных психологических исследований, относящихся и ко времени реакций, и вообще к вопросам определения сенсорной чувствительности человека. Здесь незаменимы материалы, представленные Б. Г. Ананьевым в уже упомянутом фундаментальном труде «Человек как предмет познания».

Б. Г. Ананьев пишет: «В литературе описаны значительные вариации ВР, связанные с информационной природой стимула, социальным развитием и образованием, отношением к задаче, тренированностью испытуемых и т. д. По этим диапазонам можно выделить известный оптимум временных характеристик сенсомоторных и речемыслительных реакций, который совпадает с периодом юности и молодости...» Сопоставляя этот вывод с результатами изучения чувствительности различных модальностей, полученными П. П. Лазаревым, Б. Г. Ананьев особенно подчеркивает, что пороговые значения, например относящиеся к двадцатилетнему возрасту, «...могут быть использованы в качестве эталона сенсорного оптимума, по сличению с которым можно определить возраст любого человека» [1,141], причем «с точностью до трех — пяти лет [1,141]. Далее Б. Г. Ананьев, рассмотрев особенности развития проприорецепции, зрительной и слуховой чувствительности, а также высших психических функций человеческого интеллекта, отмечает двухфазный характер одних и тех же психофизиологических функций человека» — как «одно из проявлений единства человека как индивида и личности, субъекта деятельности», причем длительность второй фазы определяется степенью активности человека как субъекта и личности» [1,142-154], — то есть степенью психологической активности, связанной с активностью социальной.

Указанная связь, по Б. Г. Ананьеву, позволяет осуществить исторический подход к личности и ее психической деятельности, представляя жизненный путь человека как историю личности и субъекта деятельности. На этой основе строятся «онтологические поиски путей построения теории личности «во времени» в противовес чисто структурным ее определениям, абстрагированным от реального временного протекания ее жизненного цикла» [1, 15], — например, генетическая теория личности П. Жане, концепция психологической эволюции личности Ш. Бюлер, генетическая классификация основных видов деятельности человека как основных ступеней его развития С. Л. Рубинштейна.

Завершая рассуждения об этих и других примерах исторического подхода к изучению личности, Б. Г. Ананьев утверждает: «Фазный характер развития социальной активности проявляется в смене состояний основной... деятельности и может быть более или менее точно определен хронологически-биографическим методом. Каждая из этих фаз: подготовительная, старт, кульминация («пик»), финиш — характеризует структурное изменение субъекта деятельности» [1, 161]. Наконец, важно подчеркнуть, что этот фазный характер активности человека рассматривается Б. Г. Ананьевым о реальном времени: «История личности и субъекта деятельности развертывается в реальном пространстве и времени онтогенеза и в известной мере ими определяется, как это видно, например, в отношении возраста. В еще большей мере важно учитывать и обратное влияние социального развития на изменение человеческой природы и жизненного пути человека, на его онтогенетическую эволюцию» [1, 162], поскольку «влияние жизненного пути человека и меры его активности на ход онтогенетической эволюции в период старения неизмеримо больше, чем в ранние годы» — сказывается эффект «все возрастающей индивидуализации этой эволюции» [1, 165].

Таким образом, поиск оснований для обобщенного, аппроксимирующего определения функций, определяющих субъективную сторону психофизических исследований, привел к тому, что вместе со стадиальными характеристиками кривых, представляющих развитие не только временных реакций, но и всевозможных других функций чувствительности, а также и высших психологических функций, мы получили совершенно четкий ответ, указывающий на приоритет временной координаты вообще, как только речь заходит об аппроксимации кривых, характеризующих функционально-структурный статус субъекта в любых исследованиях его деятельности.

Стадиальность, как представление фазного характера развития сенсорной чувствительности и социально-психологической активности субъекта — это безусловное основание для того, чтобы утверждать, что как в частном случае проявления особенностей временных реакций, так и вообще в проявлениях человеческой активности аппроксимирующей функцией должна быть только функция Гаусса—Лапласа, функция нормального распределения изучаемых феноменов относительно параметра времени.

Оставляя при этом вопрос, о каком именно времени идет речь, — о реальном, понимаемом как однозначно физическое, или о реальном времени, подразделяемом на две относительно независимые формы — физическое и психологическое, примем прежде всего, что аппроксимацией всех кривых логарифмических зависимостей является кривая нормального распределения.

§19.4. Время как параметр нормального распределения психологической активности человека

Предваряющим замечанием к нормальной аппроксимации логарифмических кривых может быть напоминание П. Фресса и Ж. Пиаже, указывающих, что еще в 1932 году Хоустон «принял для роста интенсивности видимой яркости... сигмоиду интеграла вероятности... благодаря чему распределение различительной чувствительности (величины, обратной порогу) образует колоколообразную кривую на шкале логарифмов освещенности» [5,264-265]. В нашем случае обобщенного, качественного подхода достаточно, чтобы, не воспроизводя кривую Хоустона, подчеркнуть, что она представляет собою наглядное подтверждение справедливости вывода об аппроксимирующем значении функции нормального распределения.

Добавим, что П. Фресс и Ж. Пиаже, говоря о психометрической функции, упоминают работу Галифрэ (1947), где также в отношении разностного порога для тактильной чувствительности по гистограмме частот находится их последовательное приращение, а затем столь же последовательное снижение, «...позволяя вычертить колоколообразную кривую гауссовского распределения», которая получена «графическим способом, чисто эмпирически», но если допускается «теоретическая правомерность вероятностной психометрической функции... (как это сделал Фехнер для этой функции, называемой «фи-гамма»), мы получаем право использовать математические методы для нахождениянаиболее вероятного значения. Если мы будем знать дисперсию измерений, то сможем найти интеграл — эту половину колоколообразной кривой — с помощью вычислений» [5,247]. Это заключение важно для нас, поскольку часто приводимые S-образные логарифмические и прочие кривые могут создать впечатление, что психофизические объективные и субъективные зависимости не имеют ничего общего с нормальным распределением. Между тем здесь существенно уточнить, что их следует рассматривать лишь как половину полной кривой, отражающей вначале приращение сигнала или реакции, а затем — последовательное снижение.

Приведем еще одно замечание из П. Фресса и Ж. Пиаже по поводу логарифмической кривой, представляющей меру информации: ее помещение на общую плоскость совместно с другими кривыми может вызвать оправданное замечание: нельзя соотносительную со временем величину помещать рядом с величинами, не имеющими временного определения. Но вот что говорят названные авторы: «Тесная связь между скоростью восприятия и интенсивностью ощущения бесспорна, но для полного отождествления данных пока недостаточно» [5, 274].

В нашем контексте это замечание крайне важно, так как мы стремимся в конечном счете не к упорядочению некоторых сведений психофизики или других отраслей психологии, а к выведению из этих сведении особого значения времени в оценке проявлений различных видов активности человека как личности. Поэтому мы не удовлетворяемся только одним подтверждением того, что логарифмики аппроксимируются нормальным образом, а тут же используем полученные свидетельства для перехода к основной теме наших изысканий. Речь идет о том, что временная координата является тем параметром, относительно которого и строится на самом деле, то есть в сущности, нормальное распределение объективных и субъективных психофизических зависимостей. Эти зависимости, с точки зрения сущности закона Гаусса—Лапласа, только явления, за ними необходимо постепенно эту сущность вскрыть, что, понятно, невозможно сделать, не рассматривая этих явлений подробнейшим образом.

Так насколько корректно сопоставление логарифмик психофизических с логарифмикой меры информации? К замечанию Фресса и Пиаже нужно привести какие-то дополнительные соображения, математически они могут быть представлены так. Если справедлива формула закона Хика (в известных, конечно, пределах) Y == К · log X, то не будет нарушением данного равенства и такое ее представление:



где «Т» — период наблюдений. Но тогда, при том допущении, что в принципе возможно взаимнооднозначное соответствие интенсивности сигнала и реакции, мы получаем:
Т(физическое, «объективное») = К · log X/T(психологическое, «субъективное»).
И наоборот, можно вывести за пределы формулы меры информации временной аспект, представив, что субъект воспринимает в 1 секунду всего 5 битов, и как раз столько же битов информации имеется в содержании сигнала: время, таким образом, как бы исключается из рассмотрения, а формула меры информации при такой оговорке вполне корректно может быть сопоставлена с другими логарифмическими формулами, так же, как и адекватные этим формулам кривые на соответствующих графиках.

Но не только это обстоятельство имеется в виду, когда оказывается, что мы можем вводить временные характеристики в формулы психофизики, не нарушая их математической правильности.

Еще раз обратимся к математике, чтобы уже с этой стороны была относительно завершена идея нормальной аппроксимации и чтобы вплотную перейти к вопросу о значении времени с точки зрения не только физико-математической, но и психологической.

Это обращение носит чисто справочный характер в связи с тем, что при сущностном характере нормального распределения формы его математического представления небезразличны. В обычном применении кривой нормального распределения к характеристике психологических явлений очень распространено мнение, что собственно нормальное распределение — это только то, которое «однозначно определяется всего лишь двумя параметрами, а именно: средней арифметической величиной М и среднеквадратическим отклонением s или дисперсией D и т.д. Это определение, разумеется, является правильным, но только в отношении идеального, то есть практически весьма маловероятного сочетания некоторых событий или некоторых результатов эмпирического исследования.

В природе и обществе все случайные реальные события распределены по особым законам, выражающим свойства этих событий, связанных со способами и условиями взаимодействия каких-либо объектов и характеристиками их состояний. В целом, математически, принято говорить не о событиях, а о «величинах», что, конечно, значительно обедняет смысл взаимодействия или вовсе игнорирует последнее. Это следует иметь в виду, когда возникает необходимость правильно объяснить применение законов распределения в психологических исследованиях.

Говоря математическим языком, в природе и обществе обнаруживается неограниченное множество законов распределения, аналитически, в специальных формулах представляющих знания о специфике реальных событий («случайных величин»). Множество законов соответствует множеству реальных событий, являющихся «случайными», — и это справедливо, поскольку законы и вообще необходимость появления каких-либо событий «пробивают» себе дорогу через случайности, то есть благодаря, а не вопреки им: если бы никаких случайных событий не происходило — значит, не происходило бы вообще никаких событий.

Среди неограниченного множества возможных законов распределения случайных величин особенно выделяется закон, который независимо друг от друга установили Лаплас и Гаусс. Действие этого закона является распространенным для многих реальных событий в пространстве и времени ближайшего космоса, к которому принадлежит Солнечная система и планета Земля.

Распределение событий по закону Лапласа—Гаусса исторически очень часто принималось за норму, поэтому данный закон называется иначе «законом нормального распределения». Очевидно, что именно по этому закону преимущественно распределены события, наиболее полно отражающие сущность человека, являющуюся нам в его основных психических образованиях. Характер кривой нормального распределения позволяет выделить 2 или 4, или 6 попарно одинаковых долей общей площади, охватывающей 99,72 % случаев частоты проявления психических образований человека при больших количествах наблюдений.

Особо следует обратить внимание на то, что всего 4 попарно одинаковых доли площади под кривой нормального распределения охватывают 95,44 % случаев проявления психических образований человека. В частности, в психодиагностике обычно ограничиваются допущением всего лишь четырех основных вариаций проявления свойств личности по тому или иному ее параметру. При округлении до целых чисел эти вариации последовательно размещаются в отношении медианы Meследующим образом (см. рис. 19.1).

Пример представлен с учетом допущения ошибки около 2 % случаев из 100%, что не противоречит обычным требованиям психологической практики. То есть в практической психологии может быть, вполне приемлем квазиквартильный подход, когда значения вариаций, делят вместе с медианой все множество значений на четыре подмножества. Эти значения удобнее по-прежнему называть квартилями по тождественности их смыслов, несмотря на их количественное неравенство, когда первый и четвертый квартили соответствуют 16 %, а второй и третий — 34% всех случаев проявлений изучаемых психических образований человека.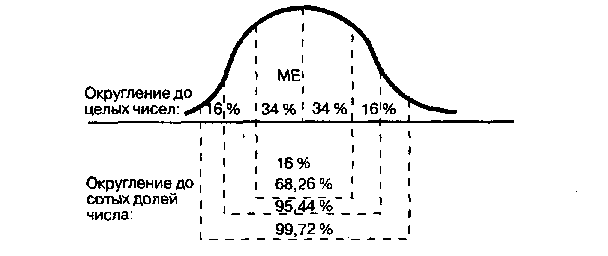


Рис. 19.1. Пример нормального распределения
Нормальное распределение — это тот идеал распределения некоторой случайной величины «S», который характеризуется плотностью ее вероятности, определяемой соответствующими хорошо известными формулами.

Общая формула нормального распределения может быть истолкована как частное выражение некоторой функциональной зависимости Y=F(x), конкретным случаем которой на самом деле и является формула плотности распределения случайной величины «S».

Таким образом, в современном математическом обеспечении психологических исследований преимущественно известна формула кривой нормального закона распределения ошибок (кривая Гаусса), представляющая собою важный, но частный случай функциональной зависимости вида:

Y = e ^–ax2. (*)

Эта исходная функциональная зависимость характеризуется тем, Что возрастает от 0 до 1 и убывает от 1 до 0, причем кривая этой зависимости симметрична относительно оси «Y» и асимптотически приближается к абсциссе (оси «X») — тем быстрее, чем больше величина «а».

Максимум рассматриваемой функции находится в точке К на оси «Y» с координатами Y = 1, X = 0. Функция имеет две точки перегиба, симметричные одна другой.

Наконец, по отношению к этим точкам перегиба могут быть точно определены наклоны касательных линий, как значения тангенсов соответствующих углов;

Данная функция может быть представлена и такими кривыми, которые являются перенесенными, сдвинутыми путем параллельного переноса как по оси «X», так и по оси «Y» или по отношению к обеим осям одновременно, но тогда, соответственно, максимум функции и все другие ее характеристики будут иметь новые, но взаимно адекватные координаты, так что общий вид кривой при этом не претерпевает изменений.

Важным применением указанной функции (*) является кривая нормального распределения ошибок, или кривая Гаусса в ее оригинальном представлении:

Рис 19.2. Кривая Гаусса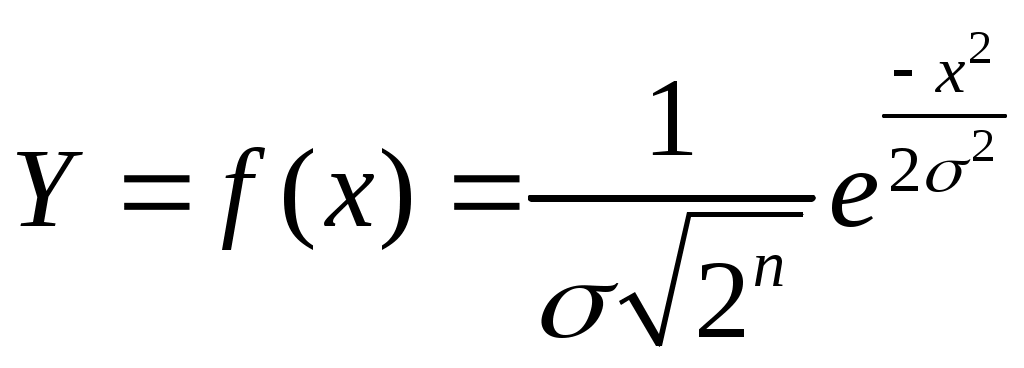


Знание того, что кривая нормального распределения, как аппроксимирующая по отношению к кривым полученным в эмпирических исследованиях, может быть переносимой с указанными ограничениями, позволяет непосредственно на графике, полученном по результатам этих исследований, оценить то, насколько, в первом приближении, качественно выполнены какие-либо экспериментальные процедуры или насколько близки к нормальному распределению эмпирические данные.

Вид кривой нормального распределения может быть получен также и в случае, если функция выражается следующим образом:

(**)

График этой функции (**) представляет собою кривую, симметричную вертикальной линии, параллельной оси Y:

Таким образом, нормальная аппроксимация кривых, представляющих некоторые закономерности, может быть осуществлена на основе различных формул, и поэтому в экспериментальной работе важное значение имеет процесс установления эмпирических зависимостей, которые, по возможности, сводятся к формулам, близким к вышеприведенным. В контексте обсуждаемых вопросов аргумент х очевидно должен будет представлять собою в этих эмпирических формулах параметр времени.