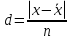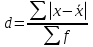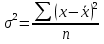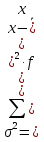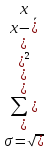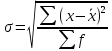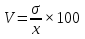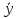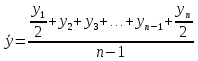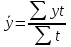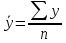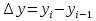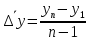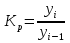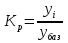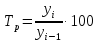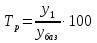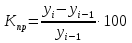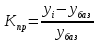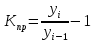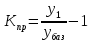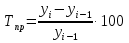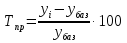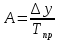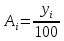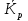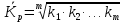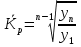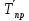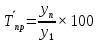Практикум по статистике. Практикум по статистике Примечание Первым делом нажать Вид
 Скачать 278.19 Kb. Скачать 278.19 Kb.
|
|
Тема 4. Показатели вариации Задачи и решения Задача 1 Распределение студентов одного из факультетов вуза по возрасту характеризуется следующими данными:
Вычислить: средний, модальный и медианный возраст, размах вариации; среднее линейное отклонение; дисперсию; среднее квадратическое отклонение; коэффициент вариации. Решение Задача 2 Средняя урожайность пшеницы характеризовалось следующими показателями (центнеров с одного гектара убранной площади).
Источник: Российский статистический ежегодник, 2006 : Стат. сб. / Росстат. – М., 2006. – С. 780. Рассчитать показатели вариации. Сравните вариации урожайности по двум странам. Решение Задача 3
Определите для каждого почтового отделения:
Решение Задача 5 Средний стаж работы в цехе равен 10 лет, дисперсия составляет 81. Определите коэффициент вариации стажа работы в цехе, сделайте выводы. Решение Задача 6 Имеются данные о распределении населения РФ по величине среднемесячного душевого дохода в 2005:
Источник: Российский статистический ежегодник, 2006. Стат. сб. / Росстат. – М., 2006. С. 188 Определить: 1) среднемесячный душевой доход по стране в целом; 2) моду; 3) медиану; 4) коэффициент вариации. Решение Задача 7 В трёх партиях продукции, представленных на контроль качества, было обнаружено:
Определите по трём партиям:
Решение Задача 8 По данным задачи 19 («Средние величины») рассчитайте: моду и медиану, а также показатели вариации. Оцените количественную однородность совокупности. Решение Основные символы и формулы
Контрольные вопросы
Тема 5. Динамические ряды Задачи и решения Задача 1 Имеются следующие данные об экспорте РФ в 2000 – 2006 гг. (млрд.долл. США).
Источник: Россия в цифрах. 2007 : Крат. стат. сб. / Росстат. – М., 2007. – С. 455. Дополните таблицу недостающими данными Решение Задача 2 Имеются данные об импорте РФ в 2000-2006 гг. (млрд.долл. США).
Источник: Россия в цифрах. 2007 : Крат. стат. сб. / Росстат. – М., 2007. – С. 455 Рассчитать:
Решение Задача 3 По одному из представленных биржевых товаров дайте краткий анализ изменения цен с помощью производных показателей динамического ряда.
Источник: Российский статистический ежегодник. 2006 : Стат. сб. / Росстат. – М., 2006. – С. 794. Решение Задача 4 Подсчитайте среднегодовые темпы роста и прироста экспорта ЕС, если известно, что в 2001 году объём экспорта составил 985 млрд.евро, а в 2006 году – 1179 млрд.евро. Решение Задача 5 Индексы физического объёма импортных товаров в странах ЕС по некоторым видам продукции составили:
Источник: External and Intra European Union Trade, Eurostat, 2007. № 4. P.52; External and Intra European Union Trade, Statitstical Yearbook 1958-2001, Eurostat, 2002. Определить: 1) преобразовать ряды базисных показателей в ряды цепных показателей; 2) подсчитать коэффициенты опережения. Решение Задача 6 По данным о численности населения и производстве продовольствия в мире рассчитайте коэффициенты опережения.
Источник: Monthly Bullitin of Statistics, New York, UN, 2005. № 6. P. 257; 2007. № 5. P. 263. Решение Задача 7 Цены на хлеб в течение года изменялось следующим образом (данные условные): к 1 апреля цена повысилась по сравнению с 1 января на 3%, к 1 октября по сравнению с 1 июля – на 18%, а к 1 января следующего года по сравнению с 1 октября – ещё на 6%. Рассчитать: 1) общий рост цен за год и средний рост цен за месяц; 2) среднемесячный рост цен в первом и втором полугодиях; 3) среднемесячный рост цен в каждом квартале. Решение Задача 8 Известно, что число отдыхающих в пансионате в январе 2007 года составило (человек):
Определить среднее число отдыхающих за январь и указать вид динамического ряда. Решение Задача 9 За 2006 год списочная численность сотрудников фирмы составила (человек):
Определите вид динамического ряда и средний показатель численности сотрудников фирмы за 2006 год. Решение Задача 10 Движение денежных сумм на расчетном счёте предприятия происходило следующим образом (млн. руб.) на 01.04. – 400 на 10.04. – 350 на 22.04. – 430 На основе приведённых условных данных определить среднедневную сумму денег на расчетном счёте предприятия за апрель. Решение Задача 11 Имеются ежемесячные данные об импорте чая за год (данные условные) в тыс. т:
Выявить тенденцию с помощью укрупнения интервалов. Произвести сглаживание по методу обычной средней. Решение Задача 12 Рассчитайте недостающее значение показателя численности населения США за 2004 год.
Источник: Monthly Bulletin of Statistics, New Tork, UN, 2006. № 6. P. 5. Решение Задача 13 На основе приведённых ниже показателей получить сопоставимые данные путём смыкания рядов динамики:
Решение Задача 14 Рассчитайте уровень занятости в Испании за 2007 год, располагая следующими данными:
Источник: Statistical annex of European economy, Spring 2007. P. 186. Решение Основные символы и формулы
Контрольные вопросы
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||