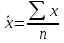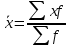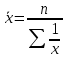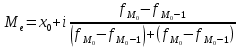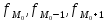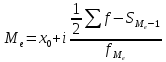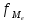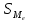Навигация по странице:Количество студентов данного возрастаЭкзаменационные оценки Отлично (5) Хорошо (4)Сделка Количество проданных акций, шт. Курс продаж, руб.Вид продукции Процент брака Стоимость бракованной продукции, руб.Группы таможенных складских помещений по площади, тыс.кв.м. Число помещений Общая занятая площадь, тыс.кв.м.Филиал Март АпрельЯнварь ФевральПредприятие с прибылью, млн.руб. Количество предприятий в 1-ой отраслиИюнь отчётного года Июль отчётного годаУчебный год Дневные общеобразовательные школы Средние специальные учебные заведенияВысшие учебные заведения Число школ, тыс. Число учащихся, тыс.Размер земельного участка, га Число хозяйств, тыс.Показатель Январь Февраль МартНомер автоколонны Грузооборот, тыс.км Средняя дальность перевозки 1 т груза, кмСтаж работы, лет До 5 5-10 10-15 15-20Основные символы и формулы
|
Практикум по статистике. Практикум по статистике Примечание Первым делом нажать Вид
Тема 3. Средние величины
Задачи и решения
Задача 1
Имеются данные о возрасте студентов академической группы №1:
Возраст студентов (лет)
|
17
|
18
|
19
|
20
|
Количество студентов данного возраста
|
4
|
4
|
4
|
4
|
Определить средний возраст студентов группы.
Решение
Задача 2
Имеются данные о возрасте студентов группы №2
Определить средний возраст студентов группы.
Решение
Задача 3
Было реализовано 5000 единиц товара А по цене 40 долларов и 300 единиц товара Б по цене 50 долларов. Определите среднюю цену реализованных товаров.
Решение
Задача 4
Сделайте расчет цены изделия по двум партиям, если известно, что стоимость первой партии – 2000 тыс.руб., второй – 10000 тыс.руб., а цена за единицу товара – 2 тыс. и 5 тыс. соответственно.
Решение
Задача 5
Фактически выпуск продукции на трёх предприятиях составил 180, 100, 200 тыс. руб., при этом уровень выполнения плана на предприятиях составил 105%, 102%, 103% соответственно. Определите средний процент выполнения плана по данным предприятиям.
Решение
Задача 6
Плановым заданием предусматривался выпуск продукции первым цехом на 4- тыс. руб., вторым – на 30 тыс. руб. Выполнение плана составило 105% и 103% соответственно. Определите средний процент выполнения плана по двум цехам предприятия.
Решение
Задача 7
Результаты экзамена по теории статистики представлены в таблице:
Экзаменационные оценки
|
Отлично
(5)
|
Хорошо
(4)
|
Удовлетворительно
(3)
|
Неудовлетворительно
(2)
|
Итого
|
Число оценок
|
6
|
15
|
4
|
2
|
27
|
Подсчитайте средний балл, полученный студентами на экзамене, а так же моду и медиану.
Решение
Задача 8
Имеются следующие условные данные о продаже акций АО на торгах фондовой биржи:
Сделка
|
Количество проданных акций, шт.
|
Курс продаж, руб.
|
1
|
500
|
1000
|
2
|
300
|
1050
|
3
|
110
|
1145
|
Сделайте расчёт среднего курса продажи акций, основываясь на свойствах средней.
Решение
Задача 9
Качество продукции предприятия в отчётном месяце характеризуется следующими данными:
Вид продукции
|
Процент брака
|
Стоимость бракованной продукции, руб.
|
А
|
1,3
|
2135
|
В
|
0,9
|
3560
|
С
|
2,4
|
980
|
Определите средний % брака по указанным видам продукции предприятия.
Решение
Задача 10
Использование таможенных складских помещений города в отчётном периоде характеризовалось следующими данными:
Группы таможенных складских помещений по площади, тыс.кв.м.
|
Число помещений
|
Общая занятая площадь, тыс.кв.м.
|
До 5
|
3
|
5,2
|
5-10
|
21
|
108,0
|
10-15
|
17
|
163,6
|
15-20
|
9
|
101,2
|
20-25
|
5
|
65,3
|
25-30
|
3
|
40,6
|
30-35
|
4
|
55,4
|
35 и более
|
2
|
29,0
|
Определите средний % загрузки таможенных складов.
Решение
Задача 11
Имеются следующие данные по трём филиалам банка:
Филиал
|
Март
|
Апрель
|
Средний размер вклада, тыс.руб.
|
Общая сумма вкладов, тыс.руб.
|
Средний размер вклада, тыс.руб.
|
Общая сумма вкладов, тыс.руб.
|
1-ый
|
13,0
|
3900,0
|
15,0
|
200,0
|
2-ой
|
22,0
|
3080,0
|
25,0
|
150,0
|
3-ий
|
60,0
|
9030,0
|
65,0
|
210,0
|
Рассчитайте средний (по трём филиалам) размер вклада за каждый месяц.
Решение
Задача 12
Имеются следующие данные о заработной плате рабочих трёх цехов завода за два месяца:
№ цеха
|
Январь
|
Февраль
|
Средняя зарплата, руб.
|
Число рабочих
|
Средняя зарплата, тыс.руб.
|
Фонд заработной платы, тыс.руб.
|
1
|
5000
|
20
|
6,0
|
180
|
2
|
7000
|
10
|
7,5
|
75
|
3
|
9000
|
30
|
19,0
|
200
|
Вычислите среднемесячную заработную плату рабочих завода за каждый месяц и в целом за 2 месяца.
Решение
Задача 13
Имеются данные о размере прибыль предприятий по отраслям:
Предприятие с прибылью, млн.руб.
|
Количество предприятий
|
в 1-ой отрасли
|
во 2-ой отрасли
|
10-30
|
10
|
20
|
40-60
|
20
|
10
|
70-80
|
30
|
5
|
Определите средний размер прибыли, приходящийся на одно предприятие: 1) по каждой отрасли; 2) по двум отраслям вместе.
Решение
Задача 14
Найти среднюю цену реализации дискет за каждый день и за два дня в целом, если известно, что в первый день было продано товара на сумму 6720 руб. по цене 12 руб. за штуку и на 4200 руб. по цене 15 руб. за штуку; во второй день по цене 12 руб. было продано 450 шт., а по цене 15 руб. – 320 шт.
Решение
Задача 15
Имеются следующие данные о заработной плате рабочих трёх цехов завода за 2 месяца:
№ цеха
|
Июнь отчётного года
|
Июль отчётного года
|
Фонд заработной платы
|
Число рабочих, чел.
|
Фонд заработной платы, тыс.руб.
|
Число рабочих, чел.
|
1
|
60
|
20
|
120,0
|
30
|
2
|
40,0
|
10
|
90,0
|
20
|
3
|
150,0
|
30
|
70,0
|
10
|
Рассчитайте среднюю з/п по каждому из цехов и в целом по трём цехам, сравните показатели за два месяца.
Решение
Задача 16
Рассчитайте все возможные виды средних величин по данным о числе учебных заведений и численности учащихся в них в России (на начало учебного года).
Учебный год
|
Дневные общеобразовательные школы
|
Средние специальные учебные заведения
|
Высшие учебные заведения
|
Число школ, тыс.
|
Число учащихся, тыс.
|
Число учебных заведений, тыс.
|
Число учащихся, тыс.
|
Число ВУЗов
|
Число студентов, тыс.
|
2000/01
|
67,0
|
20074
|
2703
|
2361
|
965
|
4741
|
2004/05
|
63,2
|
16168
|
2805
|
2600
|
1071
|
6884
|
2005/06
|
61,5
|
15183
|
2692
|
2462
|
1059
|
7010
|
Источник: Содружество Независимых Государств. 2000-2005 : Крат. стат. справочник / Статкомитет СНГ. – М., 2006. – С.44.
Решение
Задача 17
Имеются следующие данные о забастовках в РФ:
Год
|
Число организаций, на которые приходятся забастовки
|
Численность работников, участвовавших в забастовках, тыс.чел.
|
Количество времени, неотработанного участвовавшими в забастовках работниками, тыс.чел-дн.
|
1990
|
260
|
99,5
|
207,7
|
1995
|
8856
|
489,4
|
1367,0
|
2000
|
817
|
30,9
|
236,4
|
2005
|
2575
|
84,6
|
85,9
|
Источник: Российский статистический ежегодник. 2006 : Стат. сб. / Росстат. – М. 2006. – С.162.
Рассчитайте для каждого года:
среднюю численность работников, участвовавших в забастовках, в расчёте на одну организацию;
средние потери рабочего времени в расчете на одну организацию;
средние потери рабочего времени в расчете на одного участника забастовки.
Решение
Задача 18
Работа общедоступных библиотек в РФ (на конец года) характеризовалась следующими показателями:
|
1990
|
1995
|
2000
|
2005
|
Число библиотек (тыс.)
|
62,6
|
64,4
|
51,2
|
49,5
|
Библиотечный фонд (млн.экз)
|
1155
|
1105
|
1027
|
977
|
Всего зарегистрированных пользователей (млн.чел.)
|
71,9
|
60,2
|
59,6
|
58,1
|
Выдано экземпляров (млн.экз.)
|
1506
|
1325
|
1340
|
1304
|
Источнник: Российский статистический ежегодник. 2006 : Стат. сб. / Росстат. – М., 2006. 0 С.286.
Определить:
Число экземпляров в среднем на одну библиотеку;
Число экземпляров в среднем на одного пользователя;
Число зарегистрированных пользователей в среднем на одну библиотеку;
Число выданных экземпляров в среднем на одного пользователя.
Решение
Задача 19
Распределение крестьянских (фермерских) хозяйств в РФ по размеру предоставленных им земельных участков на конец 2005 года характеризуется следующими данными:
Размер земельного участка, га
|
Число хозяйств, тыс.
|
До 3
|
50,1
|
4-5
|
23,5
|
6-10
|
34,4
|
11-20
|
36,0
|
21-50
|
44,1
|
51-70
|
14,6
|
71-100
|
13,5
|
101-200
|
17,0
|
Свыше 200
|
18,1
|
Источник: Российский статистический ежегодник. 2006 : Стат. сб / Росстат. – М., 2006. – С. 444.
Определите средний размер земельного участка крестьянского (фермерского) хозяйства.
Решение
Задача 20
По распределению за I квартал известны следующие данные:
Показатель
|
Январь
|
Февраль
|
Март
|
Выпуск годной продукции, тыс.руб.
|
800,0
|
920,0
|
980,0
|
Брак, %
|
1,5
|
1,4
|
1,2
|
Определите средний процент брака за 1 квартал.
Решение
Задача 21
По трем автоколоннам транспортного предприятия за месяц известны следующие данные:
Номер автоколонны
|
Грузооборот, тыс.км
|
Средняя дальность перевозки 1 т груза, км
|
1
|
420
|
11,5
|
2
|
1200
|
12,0
|
3
|
630
|
9,2
|
Определите среднюю дальность перевозки 1 т груза по транспортному предприятии.
Решение
Задача 22
Известны данные о распределении рабочих по стажу работы:
Стаж работы, лет
|
До 5
|
5-10
|
10-15
|
15-20
|
Свыше 20
|
Число рабочих
|
200
|
1400
|
800
|
400
|
200
|
Определите средний стаж работы предприятия, используя свойство средней арифметической.
Решение
Основные символы и формулы
x
|
– индивидуальное значение усредняемого признака
|
f
|
– частота или вес
|
w = x∙f
|
n
|
– объём совокупности
|
Σf = n
|
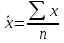
|
– средняя арифметическая простая
|
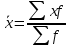
|
– средняя гармоническая простая
|
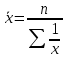
|
– средняя гармоническая взвешенная
|
M0
|
– мода
|
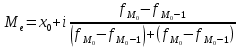
|
x0
|
– нижняя граница модального интервала;
|
i
|
– величина модального интервала;
|
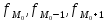
|
– частота модального, предшествующего и интервала, следующего за модальным
|
Me
|
– медиана
|
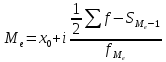
|
x0
|
– нижняя граница медианного интервала;
|
i
|
– величина медианного интервала;
|
Σf
|
– сумма частот ряда;
|
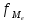
|
– частота медианного интервала;
|
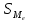
|
– сумма частот интервалов, предшествовавших медианному.
|
Контрольные вопросы
Дайте определение средней величины как обобщающей характеристики совокупности в статистике.
Какие существуют условия применения средних величин?
В чём состоит роль и значение средней величины в статистическом анализе изучаемых явлений и процессов?
Какие виды средних величин применяются в статистике?
Как следует подходить к выбору формы средней величины?
Как классифицируются средние величины на структурные и степенные?
Что такое частота в статистике, и как она влияет на выбор формулы расчёта средней величины?
Каковы основные свойства средней арифметической?
Как исчисляется средняя гармоническая, где она применяется?
Назовите условия применения сокращённого метода расчёта средней величины.
Как рассчитывается момент первого порядка? В чём заключается сущность его применения?
|
|
|
 Скачать 278.19 Kb.
Скачать 278.19 Kb.