КР_по_КП_СафароваАА_11ИПдФК1. Практикум Вариант 10 Задание 1 Посчитать сколько дней рождений выпадает на среду в зависимости от даты вашего дня рождения
 Скачать 3.74 Mb. Скачать 3.74 Mb.
|
|
Компьютерный практикум Вариант 10 Задание 1 Посчитать сколько дней рождений выпадает на среду в зависимости от даты вашего дня рождения Ход работы: Проставляем в ячейку А1 дату рождения, в ячейку В2 текущую дату, в ячейке С3 прописываем день недели (3 – среда)  В ячейке D3 – Расчет прописываем следующую формулу: =СУММПРОИЗВ(СУММЕСЛИ(C2;ДЕНЬНЕД(СТРОКА(ИНДЕКС(A:A;A$2):ИНДЕКС(B:B;B$2));2)))/C2 и нажимаем Enter.  Ответ: 1100 Задание 2 Дана формула линейной функции: y=b + ax. Известно, что а=10, b=20. Протабулировать функцию на интервале значений x от 1 до 10 с шагом 1. С помощью инструмента Подбор параметра, изменяя значение b определить, чему равен y в точке x=10, если в точке x=6 значение y=100. Ход работы: В столбец А вводим значение х от 1 до 10 с шагом 1. Для этого воспользуемся функцией «Прогрессия»  Как видим, столбец заполнен значениями с установленными шагом и границами.  Теперь нужно заполнить столбец функции f(x): y=b + ax . Для этого в первую ячейку соответствующей колонки записываем выражение по следующему шаблону: =20+10*A2 (т.к. , известно, что а=10, b=20)  Для того, чтобы произвести вычисление функции и в других строках воспользовались функцией «Автозаполнение» Задание 3 С шагом 0,1 и 0,01 изобразить на плоскости графики функций: Зададим интервал нс оси x [2;5] с шагом 0,1   Столбец значений у рассчитывается по формуле: =(B3^2-6*B3+9)/((B3-1)^2). Используя маркер автозаполнения, рассчитываем значения у для остальных х.  Строим график. Вставка Диаграмма Точечная диаграмма  Далее построим функцию с шагом 0,01  Задание 4 Исследуйте с помощью Excel наклонные асимптоты функции Область определения функции: X €(-∞; +∞) Точки пересечения: f(x)=0 0=   =0 =0 =0 =0 =-2 =-2 = - = - Асимптоты отсутствуют, нет локальных экстремумов Производная: f ’(x)=  Функция возрастает: (-∞;0)  (0;+ ∞) (0;+ ∞)Интервалы выпуклости и точки перегиба графика функции: Вторая производная: f ’’(x) = 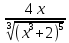 Точка перегиба: x1 =0 Функция выпукла: (-∞ ;0) Функция вогнута: (0;+ ∞) График функции:  Задание 5 Найти первую производную функции y=3cos(x^3) в точке x=  В ячейку В2 вводим заданное значение аргумента равное = ПИ()/2, в ячейку В3 введем достаточно малое приращение аргумента 0,00001, в ячейке В4 вычисляем сумму В4=В3+В2; В ячейку D3 вводим формулу для вычисления производной: =((3*COS(B4^3))-(3*COS(B2^3)))/B3; После нажатия клавиши Enter получаем результат вычисления:  Задание 6  Вводим в Excel данные: в ячейках В2:С4 указали функцию, ее точно вычисленную производную и формулу для вычисления ординаты 𝑦 касательной к графику:  Далее в ячейках В6:С8 записываем значение точки касания 𝑥0 и вычисляем значения функции 𝑓(𝑥0) и ее производной 𝑓′(𝑥0) по формулам: f(x0)= C6^3-3*C6^2+C6-8; f’(x0)= 3*C6^2-6*C6+1  Вводим параметры отображения графиков: начало и конец диапазона [-1;4] изменения 𝑥, количество 𝑁 разбиений отрезка для определения точек графика функции ∆=𝑏−𝑎𝑁 (∆=(C11-C10)/C12);  Далее сгенерируем последовательность значений 𝑥, пробегающую весь отрезок от 𝑎 до 𝑏 с шагом ∆ и вычислить в полученных точках значение функции и касательной (ячейки B15:D116): Значение ячейки В16 равно значению в ячейке С10- начало отрезка а Далее вписываем формулы: С16=B16^3-3*B16^2+B16-8 D16=$C$7+$C$8*(B16-$C$6)  Строим график функции. Выделяем весь числовой диапазон последних трех столбцов данных и выбираем в меню Вставка – Диаграммы – Точечные – Точечная с гладкими кривыми  Задание 7 Разложить в ряд Маклорена функцию f(x)=e^x. В MS Excel аппроксимировать эту функцию частичными суммами ряда Маклорена – многочленами 1-й, 2-й, 3-й, 4-й и 5-й степени. Рассмотреть интервалы [-1;1] и [-3;3] и шаги 0,1 и 0,03. На каких интервалах и шагах погрешность аппроксимации визуально наблюдается лучше всего? Решение: Разложим функцию f(x)=e^x в ряд Маклорена: 1+x+ 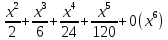 Рассмотрим интервал [-1;1] с шагом 0,1: в ячейку А2 записываем значение -1, в ячейку А3 записываем формулу =А2+0,1(продлеваем до получения 1)  Рассмотрим интервал [-1;1] с шагом 0,03: в ячейку В2 записываем -1, в ячейку В3 записываем формулу =В2+0,03 Фрагмент таблицы:  Далее рассмотрим интервал [-3;3] с шагом 0,1: в ячейку С2 ставим значение -3, в ячейке С3 записываем формулу =С2+0,1  Теперь прописываем интервал [-3;3] с шагом 0,03: в ячейку D2 записываем значение -3, в ячейку формулу =D2+0,03  Находим f(1),…f(5) на интервале [-1;1] с шагом 0,1 f(1)= A2-A2^1/ФАКТР(1) f(2)= A2-A2^1/ФАКТР(1)+A2^2/ФАКТР(2) f(3)= A2-A2^1/ФАКТР(1)+A2^2/ФАКТР(2)+A2^3/ФАКТР(6) f(4)= A2-A2^1/ФАКТР(1) +A2^2/ФАКТР(2) +A2^3/ФАКТР(6)+A2^4/ФАКТР(24) f(5)= A2-A2^1/ФАКТР(1)+A2^2/ФАКТР(2)+A2^3/ФАКТР(6)+A2^4/ФАКТР(24)+A2^5/ФАКТР(120) Находим f(1),…f(5) на интервале [-1;1] с шагом 0,03 f(1)= B2-B2^1/ФАКТР(1) f(2)= B2-B2^1/ФАКТР(1)+B2^2/ФАКТР(2) f(3)= B2-B2^1/ФАКТР(1)+B2^2/ФАКТР(2)+B2^3/ФАКТР(6) f(4)= B2-B2^1/ФАКТР(1)+B2^2/ФАКТР(2)+B2^3/ФАКТР(6)+B2^4/ФАКТР(24) f(5)= B2-B2^1/ФАКТР(1)+B2^2/ФАКТР(2)+B2^3/ФАКТР(6)+B2^4/ФАКТР(24)+B2^5/ФАКТР(120) Находим f(1),…f(5) на интервале [-3;3] с шагом 0,1 f(1)= C2-C2^1/ФАКТР(1) f(2)= C2-C2^1/ФАКТР(1)+C2^2/ФАКТР(2) f(3)= C2-C2^1/ФАКТР(1)+C2^2/ФАКТР(2)+C2^3/ФАКТР(6) f(4)= C2-C2^1/ФАКТР(1)+C2^2/ФАКТР(2)+C2^3/ФАКТР(6)+C2^4/ФАКТР(24) f(5)= C2-C2^1/ФАКТР(1)+C2^2/ФАКТР(2)+C2^3/ФАКТР(6)+C2^4/ФАКТР(24)+C2^5/ФАКТР(120) Находим f(1),…f(5) на интервале [-3;3] с шагом 0,03 f(1)= D2-D2^1/ФАКТР(1) f(2)= D2-D2^1/ФАКТР(1)+D2^2/ФАКТР(2) f(3)= D2-D2^1/ФАКТР(1)+D2^2/ФАКТР(2)+D2^3/ФАКТР(6) f(4)= D2-D2^1/ФАКТР(1)+D2^2/ФАКТР(2)+D2^3/ФАКТР(6)+D2^4/ФАКТР(24) f(5)= D2-D2^1/ФАКТР(1)+D2^2/ФАКТР(2)+D2^3/ФАКТР(6)+D2^4/ФАКТР(24)+D2^5/ФАКТР(120)  На интервалах [-1;1] с шагом 0,1и 0,03 и [-3;3] с шагом 0,1 и 0,03 визуально наблюдаются погрешности. Задание 8 Найти точки локальных экстремумов и области возрастания и убывания функции y=x*  Построим график функции x=-2…2 y= A3*КОРЕНЬ(4-A3^2)  При x= -2 функция возрастает, при x= 2 функция убывает. Локальные экстремумы x=-2 и x=2. Задание 9 Найти точки перегиба и области вогнутости и выпуклости функции y= 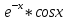 Построим график функции:  Для нахождения точек перегиба построим график второй производной  Точки перегиба: x=-7 Функция выпукла вниз |
