7класс геометрия. Праскова мария валериевна учитель математики мбоу гундинская сош

• Название: Праскова мария валериевна учитель математики мбоу гундинская сош
• Дата: 20.04.2022
• Размер: 0.88 Mb.
• Имя файла: 7класс геометрия.docx
• Тип: Документы; #486304
• страница: 3 из 6

III. Закрепление изученного материала.

1.  Учащиеся самостоятельно выполняют практическое задание № 89 (б; в).

Учитель просматривает выполнение этого задания и устраняет ошибки.

2.  Решение задачи № 90 (самостоятельно).

 

IV. Итоги урока.

Используя таблицы, учитель с помощью вопросов выясняет, умеют ли учащиеся объяснить, какая фигура называется треугольником, и назвать его элементы; знают ли, что такое периметр треугольника, какие треугольники называются равными.

Домашнее задание: изучить п. 14 из § 1; ответить на вопросы 1 и 2 на с. 49; решить задачу № 156; выполнить практическое задание 89 (а).

Урок 2. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

 Цели: разъяснить смысл слов «теорема» и «доказательство теоремы»; сформулировать и доказать первый признак равенства треугольников.

I.  Актуализация опорных знаний.

Вопросы к учащимся:

1.  Повторить определение смежных углов и их свойство.

2. Повторить определение вертикальных углов и их свойство.

3. Вспомнить определение равных фигур, биссектрисы угла.

4. Вспомнить, какой угол называется острым, прямым, тупым.

5. Повторить определение треугольника, его элементов; определение периметра треугольника; определение равных треугольников.

 II. Объяснение нового материала.

1. Разъяснение смысла слов «теорема» и «доказательство теоремы», так как с этими понятиями учащиеся встречаются впервые.

В геометрии каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.

2. Напомнить учащимся, что приведенные ранее рассуждения о свойстве смежных и о равенстве вертикальных углов были доказательствами теорем, хотя мы их еще так не называли.

3. Повторить с учащимися понятие равенства фигур (отрезков, углов, треугольников), используя при этом таблицы, модели, кодопозитивы.

4. Сформулировать и доказать теорему, выражающую первый признак равенства треугольников (это объясняет учитель).

5 . После доказательства теоремы (пункта 15) учитель разъясняет смысл слова «признак», отметив, что доказанный признак дает возможность устанавливать равенство двух треугольников, не производя фактического наложения одного из них на другой, а сравнивая только некоторые элементы треугольника.

 III. Закрепление изученного материала.

Желательно рассмотреть как можно больше задач, решаемых по готовым чертежам.

1. Решение задач (устно) по готовым чертежам на доске (учитель использует цветные мелки для выделения одним цветом равных элементов).

Задание: найдите пары равных треугольников (см. рис. 1-4) и докажите их равенство.

2. Решить задачу № 96 на доске и в тетрадях (по рис. 54).

Решение: Рассмотрим ΔАОВ и ΔДОС:

ОА = ОД (по условию); ОВ = ОС (по условию); ∠AOB = ∠ДОС (вертикальные углы равны) ⇒ ΔAОВ = ΔДОС (I признак, равны по двум сторонам и углу между ними).

Тогда ∠ДСО = ∠ABO = 74°.

∠АСД = ∠ACO + ∠ДСО = 36° + 74° = 110°.

Ответ: 110°.

3. Самостоятельно учащиеся решают задачу № 1:

Из точек А и В на прямую а опущены перпендикуляры АС и ВД, причем АС = ВД.

Д окажите, что ΔАСД = ΔВДС.

4. Задача № 2.

Дано: ΔАОВ = ΔСОД.

Доказать: ΔВОС = ΔДОА.

 IV. Итоги урока.

Домашнее задание: знать доказательство первого признака равенства треугольников п. 15, решить задачи № 93, 94 и 95.

 Урок 3. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

 Цели: выработать у учащихся умение применять при решении задач изученные свойства и теорему о равенстве треугольников по двум сторонам и углу между ними; развивать логическое мышление учащихся.

I. Проверка усвоения изученного материала.

1. Проверить знание первого признака равенства треугольников (один человек - у доски и можно три человека с листочками - за первыми партами).

2 . Два человека у доски записывают решение домашних задач № 94 и 95.

3. Устная работа с классом:

1) Контрольные вопросы 1—4 на с. 49-50.

2 ) Решение задач по готовым чертежам:

а) Какие треугольники равны на рисунке 1 и почему?

 б) На рисунке 2 в треугольниках АВД и АСД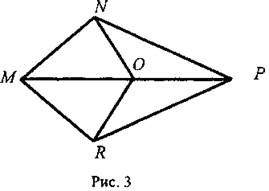

∠ ВАД = ∠САД; АВ = АС. Найдите периметр ΔАВД, если АС = 5 см, СД = 3 см, АД больше АС на 2 см.

 

в) ΔMNO = ΔMRО (рис. 3). Доказать, что ΔNOP = ΔROP.

II. Решение задач.

При построении чертежей обязательно использовать цветные мелки.

1. Решить задачу № 98 (решение объясняет учитель, привлекая учащихся).

Дано: ΔАСВ и ΔA1С1В1; АВ = А1В1; АС = А1С1; ∠A = ∠A1; AP = A1P1.

Д 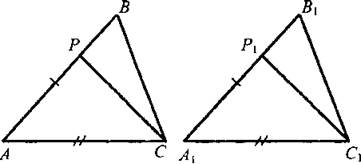оказать: ΔВPC = ΔВ1Р1С1.

 Доказательство:

Рассмотрим ΔАСВ и ΔA1С1В1:

АВ = А1В1 (по условию), АС = А1С1 (по условию),

∠A = ∠A1 (по условию), тогда ΔАСВ = ΔA1С1В1 (первый признак, равны по двум сторонам и углу между ними).

Отсюда ВС = В1С1 и ∠В и ∠B1.

По условию АВ = А1В1 и АР = А1Р1, то РВ = Р1В1.

Рассмотрим ΔВРС и ΔВ1Р1С1:

ВС = В1С1; РВ = Р1В1; ∠В = ∠B1 ⇒ ΔВРС = ΔВ1Р1С1 (первый признак, треугольники равны по двум сторонам и углу между ними).

2. Решить задачу № 99 на доске и в тетрадях.

 III. Самостоятельная работа (10 минут).

Вариант I

Докажите равенство треугольников АДС и ABC, изображенных на рисунке, если АД = АВ и ∠1 = ∠2. Найдите углы АДС и АСД, если ∠ABC = 108°, ∠ACB = 32°.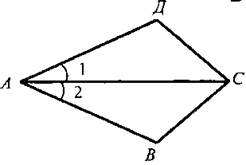

 

Вариант II

Докажите равенство треугольников ABC и АДС, изображенных на рисунке 53 учебника, если АВ = ДС и ∠4 = ∠3. Найдите углы АСВ и АДС, если ∠ABC = 102°, ∠BCA = 38°.

Вариант III (для более подготовленных учащихся)

Известно, что ∠АВС и ∠А1В1С1, причем ∠A = ∠A1, ∠B = ∠B1. На сторонах АС и А1С1 отмечены точки Д и Д1 так, что СД = С1Д1.

Докажите, что ΔСВД = ΔС1В1Д1.

Вариант IV (для более подготовленных учащихся)

Известно, что треугольник МКР равен треугольнику М1К1Р1, причем ∠М = ∠M1, ∠К = ∠К1. На сторонах МР и М1Р1 отмечены точки E и E1 так, что ME = M1E1.

Докажите, что ΔМЕК = ΔМ1Е1К1.

IV. Итоги урока.

Домашнее задание: повторить пункты 14, 15; ответить на вопросы 1—4 на с. 49—50; решить задачи № 97, 160 (a).



МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА (§ 2)

Урок 1. ПЕРПЕНДИКУЛЯР К ПРЯМОЙ. МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА

 Цели: ввести понятие перпендикуляра к прямой и доказать теорему о перпендикуляре; ввести понятия медианы, биссектрисы и высоты треугольника и научить учащихся их строить.

Наглядные пособия: таблица «Медианы, биссектрисы и высоты треугольника»; транспортиры; прямоугольные треугольники.

I.  Анализ результатов самостоятельной работы.

 II. Изучение нового материала.

1. Введение понятия перпендикуляра к прямой (рис. 55).

Учащиеся должны уяснить, что перпендикуляр АН, проведенный из точки А к прямой а, — это такой отрезок, для которого выполнены следующие два условия: 1) прямая АН перпендикулярна к прямой a (АН ⊥ а); 2) А ∉ а, Н ∈ а.

2. Выполнение практического задания 100.

3. Доказательство теоремы о перпендикуляре к прямой проводит сам учитель по рисункам 56, 57 без записи доказательства этой теоремы в тетрадях.

4. Решение задачи № 105 (устно по готовому чертежу).

5. Введение понятия медианы треугольника (использовать таблицу «Медианы, биссектрисы и высоты треугольника) и построение учащимися медиан треугольника (рис. 59).

6. Введение понятия биссектрисы треугольника и построение учащимися биссектрис углов треугольника с помощью транспортира (рис. 60).

Обратить внимание учащихся на различие между биссектрисой угла (луч, делящий угол на два равных угла) и биссектрисой треугольника (отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны).

7. Введение понятия высоты треугольника (использовать таблицу) и построение учащимися высот в остроугольном, прямоугольном и тупоугольном треугольниках с помощью прямоугольных треугольников (рис. 61 и 62).

У учащихся вызывает затруднение проведение высоты из вершины острого угла в тупоугольном треугольнике, поэтому учитель объясняет построение высот в различных тупоугольных треугольниках.

 

III. Практическая работа.

Для закрепления навыков построения медиан, биссектрис и высот треугольника учащиеся выполняют практические задания № 101, 102 и 103, а учитель просматривает выполняемые учащимися построения и оказывает необходимую помощь.

 

IV. Итоги урока.

Выяснить, какими свойствами обладают медианы, биссектрисы и высоты треугольника.

Домашнее задание: изучить пункты 16 и 17; ответить на вопросы 5-9 на с. 50; выполнить на отдельных листочках практические задания № 101, 102 и 103 и сдать учителю на проверку.

Решить задачи:

1. АС - биссектриса ∠A треугольника АВД. Докажите, что ΔВAС = ΔДАС.

2. В треугольнике АСД проведены медианы АЕ, СВ и ДF. Длины отрезков AF, ВД и СЕ соответственно равны 4 см, 3 см и 2 см. Найдите периметр треугольника АСД.

3. DN - высота треугольника MNK; МД = ДК.

Доказать, что ΔМNД = ΔKNД.



Урок 2. СВОЙСТВА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА

 Цели: закрепить изученный материал; ввести определение равнобедренного треугольника; доказать теоремы о свойствах равнобедренного треугольника.

I. Актуализация опорных знаний учащихся.

1. Фронтальный опрос по вопросам 1-9 на с. 49-50.

2. Устная проверка решения домашних задач.

II. Объяснение нового материала.

1. Определение равнобедренного треугольника; его боковые стороны и основание (рис. 63).

2. Определение равностороннего треугольника.

3. Устно решить задачи (по готовым чертежам):

1) Дан равнобедренный треугольник СДЕ с основанием ДЕ. Назовите боковые стороны, углы при основании и угол, противолежащий основанию этого треугольника.

2) В равнобедренном треугольнике МДК МК = ДК. Назовите боковые стороны, основание, угол, противолежащий основанию, и углы при основании этого треугольника.

4. Доказательство теоремы о свойствах углов при основании равнобедренного треугольника.

Чертеж, краткую запись условия и заключение теоремы, а также основные этапы доказательства полезно записать на доске и в тетрадях учащихся.

Дано: ΔАВС - равнобедренный, ВС - основание.

Доказать: ∠В = ∠С.

Доказательство: Проведем биссектрису АД треугольника (рис. 64 учебника). ΔAВД = ΔAСД по двум сторонам и углу между ними (АВ = АС по условию, АД - общая сторона, ∠1 = ∠2, так как АД - биссектриса). Значит, ∠B = ∠C, что и требовалось доказать.

Э 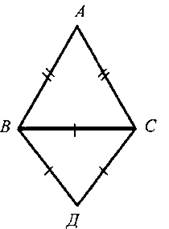то свойство в дальнейшем часто используется при решении задач и доказательстве теорем, поэтому оно должно быть хорошо усвоено.

 

III. Закрепление изученного материала.

1. Решить задачу № 108.

Дано: ΔABC - равнобедренный; ΔВСД - равносторонний.

РΔABC = 40 см; РΔBCD = 45 см.

Найти: АВ и ВС.

 Решение: ВС = СД = ВД (по условию), РΔBCD = 45 см = 3ВС, отсюда ВС = 45 : 3 = 15 (см).

По условию РΔABC = 40 см, ВС = 15 см, тогда АВ + АС = 40 - 15 = 25 (см). Так, по условию ΔABC - равнобедренный, то АВ = АС = 25 : 2 = 12,5 (см).

О 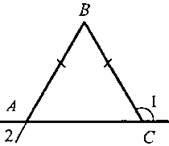твет: АВ = 12,5 см; ВС = 15 см.

2. Устно решить задачу № 116.

3. Задачу № 112 по рисунку 66 решить на доске и в тетрадях.

Дано: ΔАВС; АВ = ВС; ∠1 = 130°.

Найти: ∠2.

Решение: По условию АВ = ВС, тогда ΔABC - равнобедренный по определению, значит, ∠BAC = ∠BCA (по свойству равнобедренного треугольника). ∠BCA + ∠1 = 180° (свойство смежных углов). Отсюда ∠BCA = 180° - ∠1 = 180° - 130° = 50°; значит, и ∠BAC = 50°.

Так как ∠ВАС = ∠2 (вертикальные углы равны), то ∠2 = 50°.

Ответ: 50°.

4. Разобрать решение задачи сначала устно путем логических рассуждений, строя чертежи, а затем решение записать на доске и в тетрадях.

В равнобедренном треугольнике сумма всех углов равна 180°. Найдите углы этого треугольника, если известно, что:

а) один из них равен 105°;

б) один из них равен 38° (рассмотреть два случая).

 

IV. Итоги урока.

Домашнее задание: изучить п. 18 с доказательством теоремы об углах при основании равнобедренного треугольника; ответить на вопросы 10-12 на с. 50; решить задачи № 104, 107 и 117.



Урок 3. СВОЙСТВА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА

 Цели: изучить свойство биссектрисы (медианы, высоты) равнобедренного треугольника, проведенной к основанию; изучить признак равнобедренного треугольника и закрепить знание свойств равнобедренного треугольника при решении задач; развивать логическое мышление учащихся.

I. Проверка домашнего задания учащихся.

1. Один учащийся на доске готовит доказательство теоремы о свойстве углов при основании равнобедренного треугольника.

2. Второй учащийся решает на доске домашнюю задачу № 117 (по рис. 67).

3 . Устно по готовым чертежам на доске (см. рис. 1-3) решаем задачи, предварительно повторив материал в ходе ответов учащихся на контрольные вопросы 10-12 на с. 50.

Найдите ∠ДВА.

 

II. Изучение нового материала.

1. Сформулировать и записать признак равнобедренного треугольника (обратная теорема свойства углов равнобедренного треугольника):

Если в треугольнике два угла равны, то он равнобедренный.

2. Решить задачу № 111 (по рис. 65) устно по заранее заготовленному чертежу на доске.

3. Изучить теорему о биссектрисе равнобедренного треугольника, проведенной к основанию (рис. 64):

1) перед изучением теоремы повторить первый признак равенства треугольников; повторить определение биссектрисы, медианы и высоты треугольника; определение и свойство смежных углов треугольника;

2) учить учащихся при формулировке теоремы выделять, что дано, что надо доказать; учить краткой записи доказательства теоремы.

4. Объяснение учителя. Мы установили, что биссектриса, медиана и высота равнобедренного треугольника, проведенные к основанию, совпадают. Поэтому справедливы также утверждения:

1) Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

2) Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

5 . Устно решить задачу № 110.

 

III. Решение задач на закрепление изученного материала.

1. Решение задач (устно) по готовым чертежам (заранее изготовить плакаты с рисунками, см. рис. 1—5).

Найдите ∠ДВА (учить учащихся читать чертеж по обозначениям на нем).

2. Решить задачу № 119 с записью решения на доске и в тетрадях.

Дано: ΔДЕК - равнобедренный; EF - биссектриса; ДК = 16 см, ∠ДЕF = 43°.

Найти: KF, ∠ДЕК, ∠ЕFД.

 

Р ешение:

1) По условию EF - биссектриса ΔДЕК и ∠ДЕF = 43°, тогда ∠ДЕК = 2 · ∠ДEF = 43° · 2 = 86°.

2) EF - медиана равнобедренного ΔДЕК (по свойству биссектрисы, проведенной к основанию), тогда KF = 1/2ДК; KF = 16 : 2 = 8 (см).

3) EF - высота равнобедренного ΔДЕК (свойство биссектрисы, проведенной к основанию равнобедренного треугольника). Значит, ∠EFД = ∠EFK = 90°.

Ответ: KF = 8 см; ∠ДEK = 86°; ∠EFД = 90°.

3. Решить задачу № 120 (а) с записью решения на доске и в тетрадях.

 

IV. Итоги урока.

Домашнее задание: повторить п. 15; изучить пункты 16-18, ответить на вопросы 4-13 на с. 50; решить задачи № 114, 118 и 120 (б).

ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ (§ 3)

Урок 1. ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

 Цели: повторить и закрепить изученный ранее материал; изучить второй признак равенства треугольников и выработать навыки использования первого и второго признаков равенства треугольников при решении задач; развивать логическое мышление учащихся.

I.  Устная работа.

1. Ответы на контрольные вопросы 4-13 на с. 50.

2. Решение задач по готовым чертежам с целью повторения первого признака равенства треугольников:

1 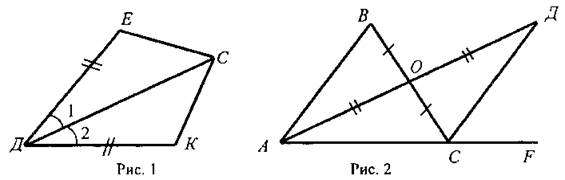) На рисунке 1 ДЕ = ДК, ∠1 = ∠2. Найдите ЕС, ∠ДCK и ∠ДKC, если КС = 1,8 дм; ∠ДCE = 45°, ∠ДEC = 115°.

2) На рисунке 2 ОВ = ОС, АО = ДО; ∠ACB = 42°, ∠ДCF = 68°.

Найдите ∠ABC.

 

II. Объяснение нового материала.

1.  Выполнение учащимися практического задания: с помощью транспортира и масштабной линейки начертить треугольник ABC так, чтобы ∠А = 46°, ∠В = 58°, АВ = 4,8 см.

2.  Формулировка и доказательство второго признака равенства треугольников (на доске и в тетрадях).

При доказательстве второго признака желательно отметить аналогию с доказательством первого признака: в том и другом случае равенство треугольников доказывается путем такого наложения одного треугольника на другой, при котором они полностью совмещаются.

 

III. Закрепление изученного материала.

1. Устно по готовым рисункам (рис. 3-7) решить задачи:

1) На рисунке 3 ∠1 = ∠2 и ∠3 = ∠4. Докажите, что ΔABC = ΔАДС.

2 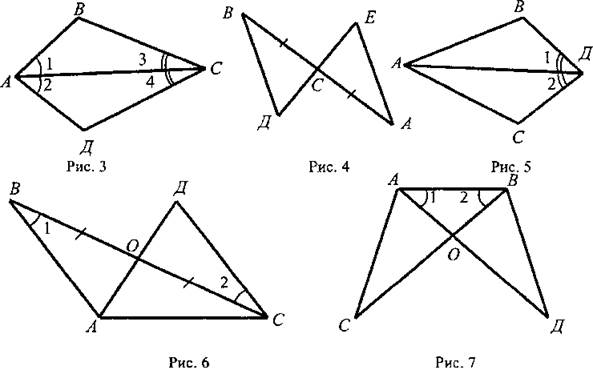) На рисунке 4 АС = СВ, ∠A = ∠B. Докажите, что ΔВСД = ΔАСЕ.

3) На рисунке 5 луч АД - биссектриса угла ВАС, ∠1 = ∠2. Докажите, что ΔАВД = ΔАСД.

4) На рисунке 6 ВО = ОС, ∠1 = ∠2. Укажите равные треугольники на этом рисунке.

5) На рисунке 7 ∠1 = ∠2, ∠CAB = ∠ДВА. Укажите равные треугольники на этом рисунке.

 2. Решить задачу № 121 (самостоятельно).

3. Решить задачу № 126 (по рис. 74).

4. Решить задачу № 127 (записать решение этой более сложной задачи на доске и в тетрадях):

 Дано: ΔАВС и ΔА1В1С1, АВ = A1B1; ВС = В1С1, ∠В = ∠В1; и Д ∈ АВ; Д1 ∈ A1B1; ∠АСД и ∠А1С1Д1.

Доказательство:

1) ΔАВС = ΔА1В1С1 по двум сторонам и углу между ними, первый признак (АВ = A1B1; ВС = В1С1, ∠В = ∠В1 по условию), значит, ∠АСВ = ∠А1С1В1.

2 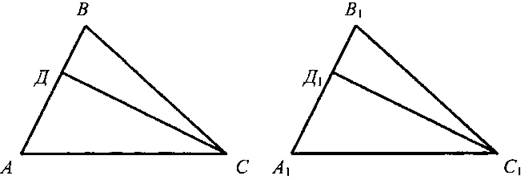) ∠ВСД = ∠АСВ - ∠АСД, ∠В1С1Д1 = ∠А1С1В1 - ∠А1С1Д1. Так как ∠АСВ = ∠А1С1В1 и ∠АСД = ∠А1С1Д1 (по условию), то ∠ВСД = ∠В1С1Д1.

3) ΔВСД = ΔВ1С1Д1 по стороне и прилежащим к ней углам, второй признак (ВС = В1С1, ∠В = ∠В1, ∠ВСД = ∠В1С1Д1), что и требовалось доказать.

 

IV. Итоги урока.

Домашнее задание: выучить доказательство теоремы из п. 19; решить задачи № 124, 125, 128.

Урок 2. ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

 Цели: изучить третий признак равенства треугольников и закрепить его знание в ходе решения задач; выработать у учащихся умение применять изученные теоремы при решении задач.

I.  Проверка домашнего задания.

1.  Обсудить решения домашних задач, ответить на вопросы учащихся.

2.  Устный опрос учащихся с использованием вопросов 1-14 на с. 49-50.

3 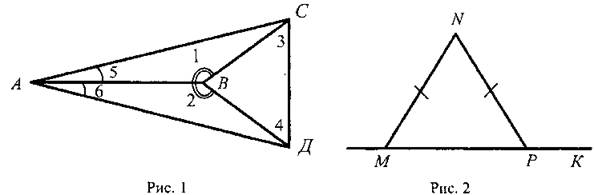.  Решение задач (устно) по готовым чертежам (см. рис. 1, 2) на применение первого и второго признаков равенства треугольников и свойств равнобедренного треугольника:

1)  На рисунке 1 ∠1 = ∠2, ∠5 = ∠6, AC = 12 см, ВД = 5 cm, ∠4 = 21°. Найдите АД, ВC и ∠3.

2)  На рисунке 2 MN = NP, ∠NPK = 152°. Найдите ∠NMP.

3)  На рисунке 70, а учебника A1С = A1C1; CB1 = C1B1. Докажите, что ΔABC = ΔABC1.

 II. Изучение нового материала.

1. Формулировка третьего признака равенства треугольников и его доказательство.

Можно дать формулировку третьего признака в таком виде: Два треугольника будут равными, если для каждой стороны одного треугольника найдется равная сторона в другом треугольнике.

Доказательство третьего признака равенства треугольников отличается от доказательств первого и второго признаков тем, что здесь не проводится наложение одного треугольника на другой. В процессе изучения теоремы о третьем признаке весьма полезна работа с рисунком 70, б и в учебника, по которому можно показать, что в случае, когда луч С1С совпадает с одной из сторон угла А1С1В1 или проходит вне этого угла, доказательство проводится аналогично случаю, когда луч С1С проходит внутри угла А1С1В1 или проходит вне этого угла, доказательство проводится аналогично случаю, когда луч С1С проходит внутри угла А1С1В1 (рис. 70, а). Можно также, после того как доказательство теоремы изложено учителем по рис. 70, а, предложить одному из учащихся доказать третий признак равенства треугольников для случая, изображенного на рисунке 70, в).

2 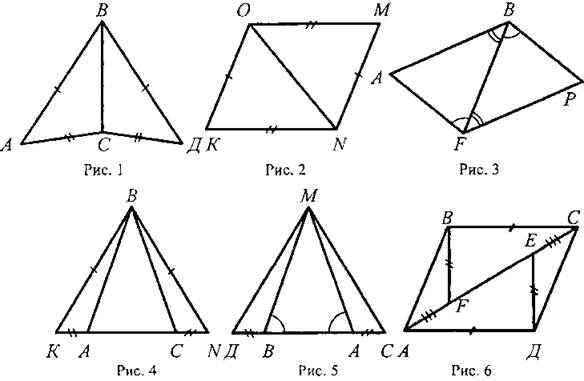. Треугольник - жесткая фигура (рис. 71 и 72).

 

III. Закрепление изученного материала.

1. Устно решить задачи по готовым чертежам (см. рис. 1-6).

Найдите пары равных треугольников и докажите их равенство (цель устной работы — учить учащихся читать чертеж по изображениям на нем равных элементов):

 2. Устно решить задачу № 135.

3. Решить задачу № 138 (по рис. 75) на доске и в тетрадях:

Дано: АВ = СД и ВД = АС.

Доказать: а) ∠САД = ∠АДВ; б) ∠ВАС = ∠СДВ.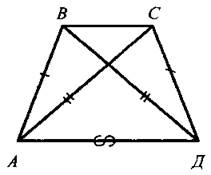

 

Доказательство:

1) Рассмотрим треугольник АВД и треугольник ДСА (можно отрезок ВС сначала стереть на доске, тогда учащиеся легко доказывают равенство этих треугольников):

АВ = СД (по условию); ВД = АС (по условию); АД - общая сторона (знак ∞) ⇒ ΔАВД - ΔДСА (третий признак по трем сторонам).

Отсюда имеем, что в равных треугольниках против равных сторон лежат равные углы, значит, ∠САД = ∠АДВ.

2) Рассмотрим треугольник ВАС и треугольник СДВ (восстанавливаем на доске отрезок ВС и стираем отрезок АД).

ВС - общая сторона этих треугольников. Аналогично доказывается равенство ΔВАС = ΔСДВ по третьему признаку. Тогда ∠ВАС = ∠СДВ.

 

IV. Итоги урока.

Домашнее задание: повторить пункты 15-19; изучить п. 20; решить задачи № 136, 137, 134.



Урок 3. РЕШЕНИЕ ЗАДАЧ

 Цели: повторить и закрепить изученный материал в ходе решения задач; учить учащихся умению применять изученные теоремы при решении задач; развивать логическое мышление.

I.  Актуализация опорных знаний.

1. Провести фронтальный опрос учащихся по вопросам 1-15 на с. 49—50 без доказательств.

2. Устное решение задач:

1) В двух треугольниках равны по две стороны и по одному углу. Всегда ли равны эти треугольники?

2) В двух треугольниках равны по одной стороне и по два угла. Всегда ли равны эти треугольники?

3) Оба треугольника равносторонние и имеют только по одной равной стороне. Равны ли эти треугольники?

4 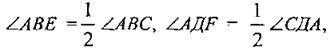) ΔСДЕ = ΔKFM и оба они равносторонние. Найдите периметр треугольника KFM, если сторона СД = 10 см.

 

II. Решение задач.

1. Решить задачу № 139 (по рис. 76) на доске и в тетрадях.

Решение (краткая запись):

1) ΔАВС = ΔСДА по трем сторонам, следовательно, ∠АВС = ∠СДА. Так как BE и DF - биссектрисы углов ABC и СДА, то  откуда следует, что ∠АВЕ =∠ADF.

2) Из равенства треугольников ABC и СДА следует, что ∠ВАЕ = ∠ДСF. Далее, ∠АВЕ = ∠АДF = ∠СДF. Итак, ∠АВЕ = ∠СДF, ∠ВАЕ = ∠ДСF и АВ = СД по условию, значит, ΔАВЕ = ΔСДF по стороне и двум прилежащим к ней углам.

2. Решить задачу № 169 (по рис. 95) на доске и в тетрадях. Рассказать учащимся о способе измерения ширины озера (отрезка АВ) по заранее изготовленной таблице: «Чтобы измерить на местности расстояние между двумя точками А и В, из которых одна (точка А) недоступна, провешивают направление отрезка АВ и на его продолжении отмеряют на земле произвольный отрезок ВС. Выбирают на местности точку О, из которой видна точка А и можно пройти к точкам В и С. Провешивают прямые ВОЕ и СОД, отмеряют на местности ДО = ОС и ОЕ = ОВ. Затем идут по прямой ДЕ, глядя на точку А, пока не найдут точку F, которая лежит на прямой АО.

Тогда FE равно искомому расстоянию. Расстояние FE измеряют на земле с помощью рулетки».

3. Решить задачу № 176* на доске и в тетрадях.

Д ано: ΔАВС = ΔA1B1C1;

АВ = А1В1; АС = А1С1; AM = А1М1.

AM и A1M1 - медианы треугольников.

Доказать: ΔАВС = ΔA1B1C1.

Доказательство:

Проведем отрезки МД = AM; М1Д1 = А1М1 и отрезки ВД; ВД1.

1)  ΔВМД = ΔСМА по двум сторонам и углу между ними, поэтому ВД = АС; ∠Д = ∠4. Аналогично ΔВ1М1Д1 = ΔС1М1А1, откуда В1Д1 = А1С1; ∠Д1 = ∠2. Отсюда следует, что ВД = В1Д1.

2)  ΔАВД = ΔА1В1Д1 по трем сторонам, поэтому ∠3 = ∠1, ∠Д = ∠Д1, значит, ∠4 = ∠2.

3 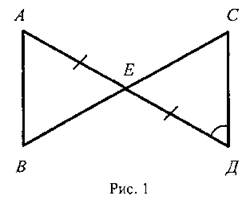)  ∠A = ∠А1, так как ∠A = ∠4 + ∠3 = ∠2 + ∠1 = ∠A1. Таким образом, ΔАВС = ΔА1В1С1 по двум сторонам и углу между ними.

 

III. Самостоятельная работа проверочного характера.

Вариант I

1. Докажите равенство треугольников АВЕ и ДСЕ на рисунке 1, если АЕ = ЕД, ∠А = ∠Д. Найдите стороны треугольника АВЕ, если ДЕ = 3 см, ДС = 4 см, ЕС = 5 см.

 2. На рисунке 2 АВ = АД, ВС = СД. Докажите, что луч АС - биссектриса угла ВАД.

В ариант II

1. Докажите равенство треугольников MON и PON на рисунке 3, если ∠MON = ∠PON, а луч NO - биссектриса ∠MNP. Найдите углы треугольника NOP, если ∠MNO = 28°, ∠NMO = 42°, ∠NOM = 110°.

2 . На рисунке 4 ДЕ = ДК, СЕ = СК. Докажите, что луч СД - биссектриса угла ЕСК.

 Дополнительно (для тех учащихся, кто более подготовлен):

В 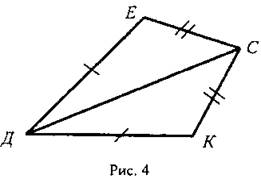треугольниках ABC и А1В1С1 АВ = А1В1, ∠А = ∠А1, ∠В = ∠В1. На сторонах ВС и В1С1 отмечены точки Д и Д1 так, что ∠САД = ∠С1А1Д1. Докажите, что: а) ΔАДС = ΔА1Д1С1; б) ΔАДВ = ΔА1Д1В1.

 

IV. Итоги урока.

Домашнее задание: повторить пункты 16-20 из § 2 и 3; решить задачи № 140; 172.

Глава II. ТРЕУГОЛЬНИКИ

ЗАДАЧИ НА ПОСТРОЕНИЕ (§ 4)

Урок 1. ОКРУЖНОСТЬ

 Цели: ввести понятие определения; систематизировать сведения об окружности, известные учащимся из курса математики предыдущих классов; уделить особое внимание отработке определения окружности и ее элементов.

I. Анализ самостоятельной работы и ее итоги.

1. Указать ошибки, сделанные учащимися при выполнении работы.

2. Решить на доске задачи, вызвавшие затруднения у учащихся.

 

II. Работа с учебником по изучению материала.

1. Ввести понятие определения.

Желательно остановиться на этом вопросе и показать учащимся, что они фактически уже встречались с определениями некоторых геометрических фигур, например, угла, треугольника, смежных углов, вертикальных углов. Повторить эти понятия.

2. Ввести определение окружности (рис. 77).

3. Самостоятельная работа учащихся по учебнику и заранее заготовленным плакатам или транспарантам (рис. 77, 78, 79-82), уделить особое внимание отработке определения окружности и ее элементов.

Систематизировать сведения, известные учащимся из курса математики предыдущих классов.

 

III. Проверка усвоения изученного материала.

1. Устно решить задачу № 143 (рис. 90).

2. Решить задачу № 144 на доске и в тетрадях.

3. Решить задачу № 146 на доске и в тетрадях.

Решение

Рассмотрим треугольник ВОС и треугольник ДОА:

АО = ОВ = ОС = ОД (радиусы окружности); ∠ВОС = ∠ДОА (вертикальные углы равны), тогда ΔBOC = ΔДОА (первый признак, по двум сторонам и углу между ними).

Значит, АД = СВ = 13 см, АО = ОВ = ОД = 16 : 2 = 8 (см); тогда РΔДОА = АД + АО + ОД = 13 + 8 + 8 = 29 (см).

Ответ: 29 см.

4.  Решить задачу № 147 на доске и в тетрадях.

Указание: рекомендовать учащимся после изображения окружности начертить прямой угол с вершиной в точке О - центре этой окружности, а затем отметить на окружности точки А и В пересечения сторон прямого угла с окружностью.

 

IV. Самостоятельная работа обучающего характера.

Вариант I

Отрезки КМ и EF являются диаметрами окружности с центром О. Докажите, что: a) ∠FEM = ∠КМЕ; б) отрезки КЕ и MF равны.

Вариант II

Отрезки ME и РК являются диаметрами окружности с центром О. Докажите, что: а) ∠ЕМР = ∠МРК; б) отрезки МК и РЕ равны.

Вариант III

В окружности с центром О проведены диаметр АС и радиус ОВ так, что хорда ВС равна радиусу. Найти ∠АОВ, если ∠ВСО = 60°.

Вариант IV

В окружности с центром О проведены хорды АВ и СД. Докажите, что АВ = СД, если ∠АОС = ∠ВОД.

V. Итоги урока.

Домашнее задание: изучить п. 21 из § 4; ответить на вопрос 16 на с. 50; решить задачи № 145, 162. Обязательно принести на следующий урок циркули и линейки.

 Урок 2. ПОСТРОЕНИЕ ЦИРКУЛЕМ И ЛИНЕЙКОЙ. ПРИМЕРЫ ЗАДАЧ НА ПОСТРОЕНИЕ

 Цели: дать представление о новом классе задач - построение геометрических фигур с помощью циркуля и линейки без масштабных делений - и рассмотреть основные (простейшие) задачи этого типа.

I.  Вводная беседа учителя.

Мы уже имели дело с геометрическими построениями: проводили прямые, откладывали отрезки, равные данным, чертили углы, треугольники и другие фигуры с помощью различных инструментов. При построении отрезка заданной длины использовалась линейка с миллиметровыми делениями, а при построении угла заданной градусной меры - транспортир.

Но, оказывается, многие построения в геометрии могут быть выполнены с помощью только циркуля и линейки без делений.

В дальнейшем, говоря о задачах на построение, мы будем иметь в виду именно такие построения.

Задачи на построение циркулем и линейкой являются традиционным материалом, изучаемым в курсе планиметрии. Обычно эти задачи решаются по схеме, состоящей из четырех частей (посмотреть с. 95-96 учебника). Сначала рисуют (чертят) искомую фигуру и устанавливают связи между данными задачи и искомыми элементами. Эта часть решения называется анализом. Она дает возможность составить план решения задачи.

Затем по намеченному плану выполняется построение циркулем и линейкой.

После этого нужно доказать, что построенная фигура удовлетворяет условиям задачи.

И наконец, необходимо исследовать, при любых ли данных задача имеет решение и если имеет, то сколько решений.

В тех случаях, когда задача достаточно простая, отдельные части, например анализ или исследование, можно опустить.

В VII классе мы решим простейшие задачи на построение циркулем и линейкой, в других классах будем решать более сложные задачи.

 

II. Построение с помощью циркуля и линейки.

Отработать навыки решения простейших задач на построение циркулем и линейкой, рассмотренных в учебнике:

1. На данном луче от его начала отложить отрезок, равный данному.

2. Отложить от данного луча угол, равный данному.

3. Построить биссектрису данного неразвернутого угла.

4. Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.

5. Построить середину данного отрезка.

6. Даны прямая и точка, не лежащая на ней. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой (решение в учебнике задачи № 153).

7. Решить задачи № 148, 150, 155.

 

III. Итоги урока.

Домашнее задание: ответить на вопросы 17-21 на с. 50; решить задачи № 149, 154; повторить материал пунктов 11-21.

ЗАДАЧИ НА ПОСТРОЕНИЕ (§ 4)

Урок 3. РЕШЕНИЕ ЗАДАЧ (2 часа)

 Цели: закрепить навыки в решении задач на применение признаков равенства треугольников; продолжить выработку навыков решения задач на построение с помощью циркуля и линейки.

I. Проверка усвоения учащимися материала.

1. Письменная работа на листочках по проверке решения задач на построение циркулем и линейкой:

Вариант I

1) Отложить от данного луча угол, равный данному.

2) Построить середину данного отрезка.

Вариант II

1) Построить биссектрису данного неразвернутого угла.

2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.

2. Проверить решение домашней задачи № 149 на доске.

Решение:

А 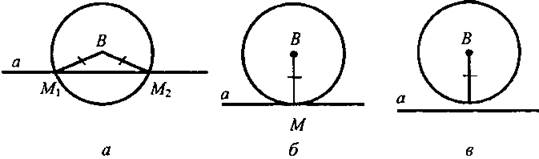кцентируем внимание учащихся на том, что вначале необходимо начертить все фигуры, данные в условии задачи. В данной задаче чертим прямую а, отрезок PQ и отмечаем точку В так, что В ∉ а. Далее проводим окружность радиуса PQ с центром в точке В. Пусть М - одна из точек пересечения этой окружности с прямой а. Точка М искомая, так как М ∈ а и ВМ = PQ. Остается выяснить, всегда ли задача имеет решение. Ответ на этот вопрос учащиеся могут дать с помощью рисунка:

Указание: задача (в) не имеет решений.

 

II. Решение задач.

1 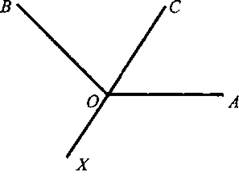. На доске и в тетрадях решить задачу № 152.

 Решение: Начертим тупой угол АОВ, построим биссектрису ОС этого угла и проведем продолжение ОХ луча ОС. Луч ОХ искомый. Убедимся в этом. По построению ОС - биссектриса ∠АОВ, поэтому∠AOC = ∠СОВ = 1/2∠AОВ и углы АОС и СОВ острые. По построению углы АОС и АОХ, а также углы СОВ и BOX смежные. Сумма смежных углов равна 180°, поэтому из равенства ∠АОС = ∠ВОС следует, что ∠AОХ = ∠ВОХ. Так как углы АОС и СОВ острые, то смежные с ними углы АОХ и BOX тупые.

2. Решить задачу № 165 на доске и в тетрадях.

Указание: первая часть решения задачи (пункт а) не вызывает затруднений у учащихся.

Для доказательства того факта, что точка О лежит на прямой КК1 (пункт б), надо рассмотреть луч ОК2, являющийся продолжением луча ОК, и доказать, что лучи ОК1 и ОК2 совпадают. Тем самым будет доказано, что точки К, O и К1 лежат на одной прямой.

 

III. Самостоятельная работа (10 минут).

В 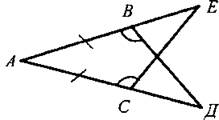ариант I

1. На рисунке АВ = АС и ∠АСЕ = ∠АВД.

1) Докажите, что ΔАСЕ = ΔАВД.

2) Найдите стороны треугольника АВД, если АЕ = 15 см, ЕС = 10 см, АС = 7 см.

2. Известно, что в треугольниках ABC и A1B1C1 ∠A = ∠A1, АВ = A1B1, АС = A1С1. На сторонах ВС и B1C1 отмечены точки К и К1 такие, что СК = С1К1. Докажите, что ΔАВК = ΔА1В1К1.

В 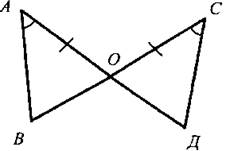ариант II

 1. На рисунке АО = СО и ∠BAO = ∠ДСО.

1) Докажите, что ΔАОВ = ΔСОД.

2) Найдите углы ΔАОВ, если ∠ОСД = 37°, ∠ОДC = 63°, ∠СОД = = 80°.

2. Известно, что в треугольниках ABC и A1B1C1 ∠В = ∠В1, АВ = A1B1, ВС = В1С1. На сторонах АС и А1C1 отмечены точки Д и Д1 так, что АД = А1Д1. Докажите, что ΔВДС = ΔВ1Д1С1.

Вариант III (для более подготовленных учащихся)

В равнобедренном треугольнике ABC с основанием АС биссектрисы АА1 и СС1 пересекаются в точке О. Докажите, что прямая ВО перпендикулярна к прямой АС.

Вариант IV (для более подготовленных учащихся)

В равнобедренном треугольнике ABC с основанием ВС медианы ВД и СЕ, проведенные к боковым сторонам, пересекаются в точке М. Докажите, что прямые AM и ВС перпендикулярны.

 

IV. Итоги урока.

Домашнее задание: подготовиться к устному опросу по карточкам, повторив материал пунктов 15-20; решить задачи № 158, 166.



Урок 4. РЕШЕНИЕ ЗАДАЧ

 Цели: закрепить навыки в решении задач на применение признаков равенства треугольников; проверить знания учащихся; подготовить учащихся к предстоящей контрольной работе.

I. Анализ самостоятельной работы.
 II. Устный опрос учащихся по карточкам.

Вариант I

1. Сформулируйте первый признак равенства треугольников.

2. На рисунке 1 АВ = ДВ, ∠1 = ∠2. Докажите, что ΔABC = ΔДВС.

3. В треугольниках ABC и A1B1C1 АВ = А1В1; АС = А1С1 и ∠А = ∠А1. На сторонах АС и А1С1 отмечены точки Д и Д1 так, что СД = С1Д1. Докажите, что ΔАВД = ΔA1B1Д1.

Вариант II

1. Сформулируйте второй признак равенства треугольников.

2. На рисунке 2 ∠1 = ∠2, ∠3 = ∠4. Докажите, что ΔАВД = ΔСВД.

3. В треугольниках ABC и A1B1C1  проведены биссектрисы АД и А1Д1. Докажите, что ΔABC = ΔA1B1C1, если ДС = Д1С1, ∠C = ∠С1, ∠АДС = ∠А1Д1С1.

Вариант III

1. Сформулируйте третий признак равенства треугольников.

2. На рисунке 3 АВ = ДС, ВС = АД. Докажите, что ΔАВС = ΔСДА.

3. На рисунке 4 АВ = ДС, ВК = ДМ, AM = СК. Докажите, что ΔАДМ = ΔСВК.

Вариант IV

1. Сформулируйте свойство углов равнобедренного треугольника.

2. На рисунке 5 АВ = ВС, АД = ДС. Докажите, что ∠ВАД = ∠ВСД.

3. В равнобедренном треугольнике ABC на основании АС взяты точки Д и Е так, что АД = СЕ. Докажите, что треугольник ДВЕ равнобедренный.

Вариант V

1. Сформулируйте свойство биссектрисы, проведенной к основанию равнобедренного треугольника.

2. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса ВД, ∠АВД = 37°, АС = 25 см. Найдите ∠В, ∠ВДС и ДС.

3 . В равнобедренном треугольнике СДЕ с основанием ДЕ проведена биссектриса CF. Найдите CF, если периметр треугольника СДЕ равен 84 см, а треугольника CFE равен 56 см.

 III. Решение задач.

1. Задача 1 (решение объясняет учитель на доске).

В равнобедренном треугольнике основание относится к боковой стороне как 3 : 4. Найдите стороны этого треугольника, если периметр его равен 33 см.

Д 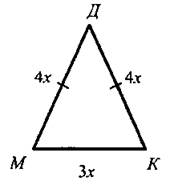ано : ΔМДК; МД = ДК; МК : МД = 3 : 4; Р = 33 см

Найти: МК, МД, ДК.

 Решение:

Пусть на одну часть приходится х см, тогда МК = 3х см, МД = ДК = 4х см. По условию Р = 33 см, значит, 3х + 4х + 4х = 33; 11х = 33; х = 3.

МК = 9 см, МД = ДК = 12 см.

Ответ: 9 см; 12 см; 12см.
2. Задача 2 (самостоятельно).

В равнобедренном треугольнике боковая сторона относится к основанию как 2 : 3. Найдите стороны треугольника, если периметр его равен 28 см.
3. Решить задачу № 175*.

З 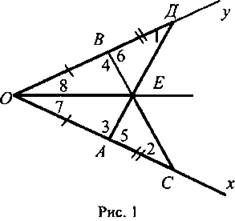апись решения задачи значительно упрощается, если ввести цифровые обозначения углов, как показано на рисунке 1.

 

Решение

1) ΔОАД = ΔОВС по двум сторонам и углу между ними, поэтому ∠1 = ∠2; ∠3 = ∠4.

2) Углы 3 и 5, а также 4 и 6 являются смежными, поэтому из равенства ∠3 = ∠4 следует, что ∠5 = ∠6.

3) ΔДВЕ = ΔСАЕ по стороне и двум прилежащим углам, поэтому BE = АЕ.

4) ΔОАЕ = ΔОВЕ по трем сторонам, значит, ∠7 = ∠8, то есть ОЕ - биссектриса угла ХОУ.

Д 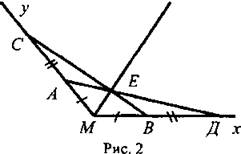ля построения биссектрисы произвольного угла М на его сторонах откладываем отрезки МА = MB, АС = ВД, как показано на рисунке 2, и проводим отрезки АД и ВС. Затем проводим искомый луч ME, где Е - точка пересечения отрезков АД и ВС.

 

 

IV. Итоги урока.

Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 15-23; решить задачи № 170, 171.

Урок 5. КОНТРОЛЬНАЯ РАБОТА № 2 (1 час)

 Цель: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.

I.  Организация учащихся на выполнение работы.

 II. Выполнение работы по вариантам.

Вариант I

1.  На рисунке 1 отрезки АВ и СД имеют общую середину О. Докажите, что ∠ДАО = ∠CBO.

2.  Луч АД - биссектриса угла А. На сторонах угла А отмечены точки В и С так, что ∠АДВ = ∠АДС. Докажите, что АВ = АС.

3.  Начертите равнобедренный треугольник ABC с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.
Вариант II

1.  На рисунке 2 отрезки ME и РК точкой Д делятся пополам. Докажите, что ∠КМД = ∠РЕД.

2.  На сторонах угла Д отмечены точки М и К так, что ДМ = ДК. Точка Р лежит внутри угла Д и РК = РМ. Докажите, что луч ДР - биссектриса угла МДК.

3.  Начертите равнобедренный треугольник ABC с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.
Вариант III (для более подготовленных учащихся)

1.  На рисунке 3 прямые АВ и СД пересекаются в точке Е, СЕ = BE, ∠C = ∠В; АА1 и ДД1 - биссектрисы треугольников АСЕ и ДВЕ.

Докажите, что АА1 = ДД1.

2. На сторонах угла А отмечены точки В и С так, что АВ = АС. Точка М лежит внутри угла А и MB = МС. На прямой AM отмечена точка Д так, что точка М лежит между точками A и Д. Докажите, что ∠ВМД = ∠СМД.

3. Начертите равнобедренный тупоугольный треугольник ABC с основанием ВС и с тупым углом А. С помощью циркуля и линейки проведите:

а) высоту треугольника ABC из вершины угла В;

б) медиану треугольника ABC к стороне АВ;

в) биссектрису треугольника ABC угла А.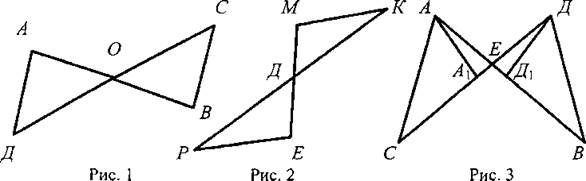

 



 

 

III. Итоги урока.

Домашнее задание: повторить материал пунктов 2-21.